2.6 直角三角形(1)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 2.6 直角三角形(1)(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 333.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-06 00:00:00 | ||
图片预览



文档简介
浙江版八年级数学上册第2章特殊三角形2.6直角三角形
第1课时 直角三角形(1)
【知识清单】
1、定义
有一个角为90°的三角形,叫做直角三角形.
2、性质
直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质.
(1)直角三角形两个锐角互余;?
(2)直角三角形斜边上的中线等于斜边的一半.?
【经典例题】
例题1,如图,在△ABC中,AB=AC,∠BAC=120°,EF为AC的垂直平分线,EF交BC于点F,交AC于点E.若BC=3a,求CF的长.
【考点】等腰三角形的性质,等边三角形的性质和判定,线段垂直平分线的性质.
【分析】作AB的垂直平分线MN,交BC于点N,交AB于点M.根据垂直平分线的性质,可得求出∠B=∠BAN=30°,∠C=∠CAF=30°,BN=AN,CF=AF,所以∠NAF=∠BAC-∠BAN-∠CAF
=120°-30°-30°=60°,∠ANF=∠B+∠BAN=60°,进而推出,△ANF是等边三角形,BN=NF=FC,FC=a.
【解答】作AB的垂直平分线MN,交BC于点N,交AB于点M.
∵AB=AC, ∠BAC=120°,
∴∠B=∠C=30°
∵MN、EF分别是AB和AC的垂直平分线,
∴∠B=∠BAN=30°,∠C=∠CAF=30°,BN=AN,CF=AF,
∴∠NAF=∠BAC-∠BAN-∠CAF=120°-30°-30°=60°,
∵∠ANF=∠B+∠BAN=60°,
∴△ANF是等边三角形,
∴,
∴FC=a.
【点评】本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等腰三角形的性质和等边三角形的性质和判定,熟记各性质是解题的关键.
例题2,如图,∠ABD=∠ACD=90°,连接BC、AD,点E,G分别是AD,BC的中点,则EG与BC的位置关系如何?请说明理由.
【考点】等腰三角形的性质、直角三角形的性质.
【分析】连接BE,CE,根据∠ABD=∠ACD=90°,
且E为AD中点,可得∴,,
所以△BEC是等腰三角形,再利用等腰三角形的三线合一的性质即可得出结论.
【解答】连接BE,CE,
∵∠ABD=∠ACD=90°,且E为AD中点,
∴,,
∴BE=CE,
∵G为BC的中点,
∴EG⊥BD.
【点评】此题主要考查直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质等知识点,解答此题的关键得出△BEC是等腰三角形.
【夯实基础】
1、在ΔABC中,,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
2、在△ABC中,AB=AC,延长BA到D,使DA=AB,连结CD,则△BDC是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不能确定
3、在ΔABC中,∠C=90°,BD、AD分别是∠CBA和∠CAB的平分线,相交于点D,则∠D等于( )
A.90° B.115° C.135° D.150°
4、在△ABC中,∠A∶∠B∶∠C=2∶3∶5,则∠C的度数是( ).
A.60° B.75° C.80° D.90°
5、如图,△ABC和△ABD都是直角三角形,∠ACB=∠ADB=90°,点E为AB的中点,连接CE、CD、DE,若∠ABC+∠DAB=65°,则∠ECD的度数是 .
6、如图,在Rt△ABC中,∠BAC=90°.
(1)若AD是BC上的高,则图中直角的个数是__ ,它们分别是__ __;
(2)若AE为BC边上的中线,BC=12 cm,则AE=______cm,图中∠C相等的角是 ;
(3)∠C=3∠B+10°,则∠EDA=_______.
7、直角三角形斜边上的高与中线分别为8cm和10 cm,则它的面积是_____cm2.
8、如图,△ABC和△ECD都是等腰直角三角形,∠ACB=90°,连接AD、BE.
(1)求证:AD=BE;
(2)BE与AD垂直吗?并说明理由.
【提优特训】
9、若三角形的一个内角等于其他两个内角的差,那么这个三角形是( ).
A.等腰三角形 B.直角三角形 C.等边三角形 D.不能确定
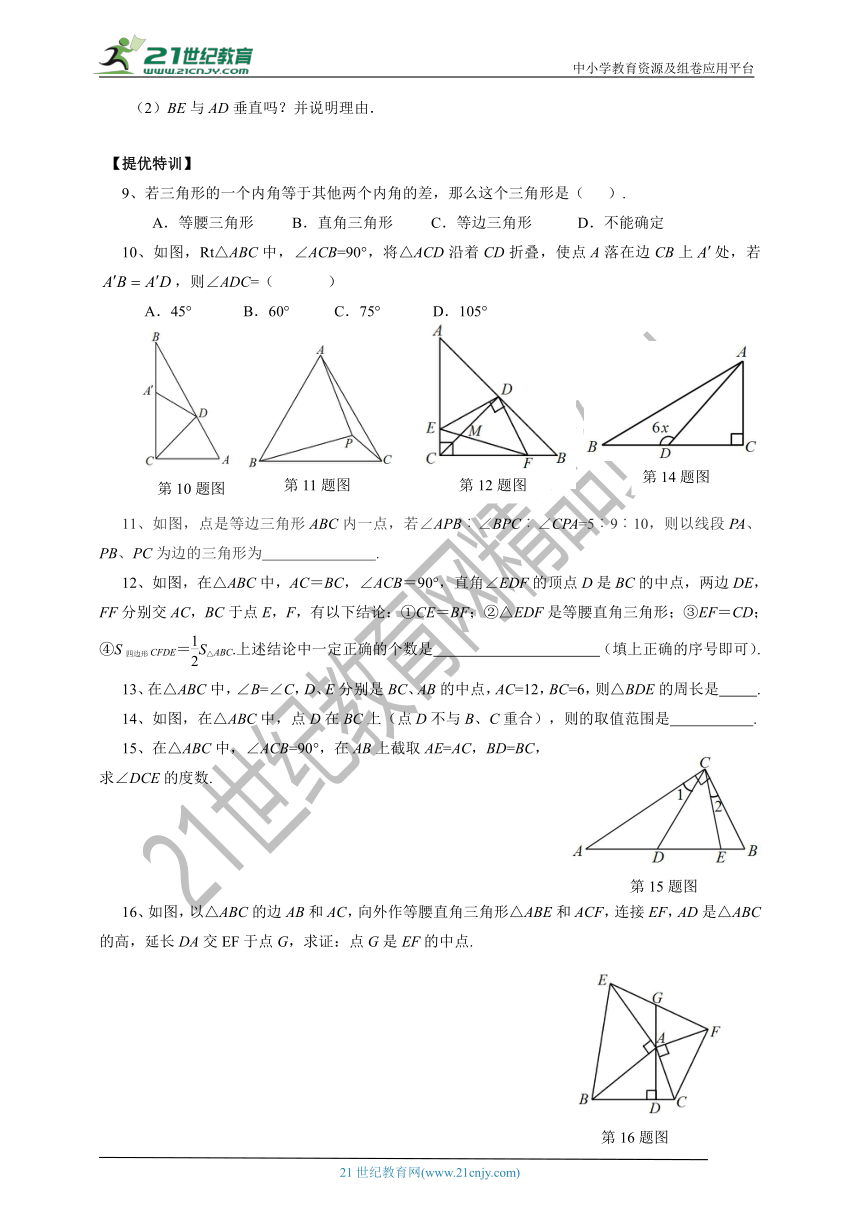
10、如图,Rt△ABC中,∠ACB=90°,将△ACD沿着CD折叠,使点A落在边CB上处,若,则∠ADC=( )
A.45° B.60° C.75° D.105°
11、如图,点是等边三角形ABC内一点,若∠APB︰∠BPC︰∠CPA=5︰9︰10,则以线段PA、PB、PC为边的三角形为 .
12、如图,在△ABC中,AC=BC,∠ACB=90°,直角∠EDF的顶点D是BC的中点,两边DE,FF分别交AC,BC于点E,F,有以下结论:①CE=BF;②△EDF是等腰直角三角形;③EF=CD;④S四边形CFDE=S△ABC.上述结论中一定正确的个数是 (填上正确的序号即可).
13、在△ABC中,∠B=∠C,D、E分别是BC、AB的中点,AC=12,BC=6,则△BDE的周长是 .
14、如图,在△ABC中,点D在BC上(点D不与B、C重合),则的取值范围是 .
15、在△ABC中,∠ACB=90°,在AB上截取AE=AC,BD=BC,
求∠DCE的度数.
16、如图,以△ABC的边AB和AC,向外作等腰直角三角形△ABE和ACF,连接EF,AD是△ABC的高,延长DA交EF于点G,求证:点G是EF的中点.
17.如图,在△ABC中,AB=AC,∠A=90°,CD平分∠ACB,E在AC上,且AE=AD,EF⊥CD交BC于点F,交CD于点O.求证:BF=2AD.
【中考链接】
18、2018扬州7.在中,,于,平分交于,则下列结论一定成立的是( )
A. B. C. D.
19、2018淄博11.(4分)如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4 B.6 C. D.8
20、2017武汉10.如图,在Rt△ABC中,∠C=90°,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A.4 B.5 C. 6 D.7
【答案】C
考点:画等腰三角形.
解答:如图①以B为圆心,BC的长为半径画弧,交AB于点D,△BCD就是等腰三角形;
如图②以A为圆心,AC的长为半径画弧,交AB于点E,△ACE就是等腰三角形;
如图③以C为圆心,BC的长为半径画弧,交AC于点F,△BCF就是等腰三角形;
如图④作AC的垂直平分线交AB于点H,△ACH就是等腰三角形;
如图⑤作AB的垂直平分线交AC于点G,△AGB就是等腰三角形;
如图⑥作BC的垂直平分线交AB于点I,△BCI就是等腰三角形.
参考答案
1、C 2、B 3、C 4、D 5、65° 6、(1)3个,∠BAC 、∠BDA、∠CDA;(2)6cm,∠EAC、∠BAD; (3)50° 7、80 9、B 10、C 11、直角三角形 12、①、②、④ 13、15
14、 18、C 19、B 20、C
8、证明:(1)△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,
AC=BC,DC=EC
在△ACD和△BCE中,
∵
∴△ACD≌△BCE(SAS).
∴AD=BE(全等三角形对应边相等).
(2)BE与AD垂直.理由如下:
由(1)△ACD≌△BCE,
∴∠ADC=∠BEC(全等三角形对应角相等).
在△BCE中,∠ACB=90°,
∠EBC+∠BEC=90°,
∠EBC+∠ADC=90°.
BE⊥AD.
15、证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵AC=AE,
∴∠ACE=∠AEC,
∵∠ACE=∠1+∠DCE,∠AEC=∠2+∠B,
∴∠1+∠DCE=∠2+∠B①.
∵BD=BC,
同理∠2+∠DCE =∠1+∠A②.
由①+②,∠1+∠DCE+∠2+∠DCE =∠2+∠B+∠1+∠A.
得2∠DCE=∠A+∠B.
∴∠DCE==45°.
16、证明:过点E作EM⊥DG的延长线于M,过点F作FN⊥DG于N.
∴∠EMA=∠FNG=90°(辅助线的作法)
∵△ABE是等腰直角三角形,
∴∠BAE=90°,AB=AE.
∴∠BAD+∠EAM=90°.
∵AD是△ABC的高,
∴∠DBA+∠BAD=90°.
∴∠DBA=∠MAE.
在△ABD和△EAM中,
∵
∴△ABD≌△EAM(AAS).
∴AD=EM(全等三角形对应边相等).
同理 △ACD≌△FAN.
∴AD=FN
∴EM=FN
在△EMG和△FNG中,
∵
∴△EMG≌△FNG(AAS).
∴EG=FG(全等三角形对应边相等).
∴点G是EF的中点.
17 、证明:连结DF,过点D作DG⊥BC于点G.
∵∠A=90°,AD=AE,AB=AC,
∴∠ADE=∠AED=45°,
∠B=∠ACB=45°,
∴∠ADE=∠B,∴DE∥BC,
∴∠EDC=∠BCD.
∵CD平分∠ACB,
∴∠BCD=∠ACD,
∴∠EDC=∠ACD,∴DE=EC.
∵EF⊥CD,∴EF垂直平分CD.
∴FD=FC,∴∠FDC=∠FCD.
∴∠FDC=∠ACD,∴DF∥AC.
∴∠DFB=∠ACB=45°.
∴∠B=∠BFD=45°,∴BD=DF,∠BDF=90°,
∴△DBF为等腰直角三角形.
∵DG⊥BF,∴DG为斜边BF上的中线,
∴DG=BF.
又∵CD平分∠ACB,∠A=∠DGC=90°,
∴AD=DG.
∴AD=BF,即BF=2AD.
第1课时 直角三角形(1)
【知识清单】
1、定义
有一个角为90°的三角形,叫做直角三角形.
2、性质
直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质.
(1)直角三角形两个锐角互余;?
(2)直角三角形斜边上的中线等于斜边的一半.?
【经典例题】
例题1,如图,在△ABC中,AB=AC,∠BAC=120°,EF为AC的垂直平分线,EF交BC于点F,交AC于点E.若BC=3a,求CF的长.
【考点】等腰三角形的性质,等边三角形的性质和判定,线段垂直平分线的性质.
【分析】作AB的垂直平分线MN,交BC于点N,交AB于点M.根据垂直平分线的性质,可得求出∠B=∠BAN=30°,∠C=∠CAF=30°,BN=AN,CF=AF,所以∠NAF=∠BAC-∠BAN-∠CAF
=120°-30°-30°=60°,∠ANF=∠B+∠BAN=60°,进而推出,△ANF是等边三角形,BN=NF=FC,FC=a.
【解答】作AB的垂直平分线MN,交BC于点N,交AB于点M.
∵AB=AC, ∠BAC=120°,
∴∠B=∠C=30°
∵MN、EF分别是AB和AC的垂直平分线,
∴∠B=∠BAN=30°,∠C=∠CAF=30°,BN=AN,CF=AF,
∴∠NAF=∠BAC-∠BAN-∠CAF=120°-30°-30°=60°,
∵∠ANF=∠B+∠BAN=60°,
∴△ANF是等边三角形,
∴,
∴FC=a.
【点评】本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等腰三角形的性质和等边三角形的性质和判定,熟记各性质是解题的关键.
例题2,如图,∠ABD=∠ACD=90°,连接BC、AD,点E,G分别是AD,BC的中点,则EG与BC的位置关系如何?请说明理由.
【考点】等腰三角形的性质、直角三角形的性质.
【分析】连接BE,CE,根据∠ABD=∠ACD=90°,
且E为AD中点,可得∴,,
所以△BEC是等腰三角形,再利用等腰三角形的三线合一的性质即可得出结论.
【解答】连接BE,CE,
∵∠ABD=∠ACD=90°,且E为AD中点,
∴,,
∴BE=CE,
∵G为BC的中点,
∴EG⊥BD.
【点评】此题主要考查直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质等知识点,解答此题的关键得出△BEC是等腰三角形.
【夯实基础】
1、在ΔABC中,,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
2、在△ABC中,AB=AC,延长BA到D,使DA=AB,连结CD,则△BDC是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不能确定
3、在ΔABC中,∠C=90°,BD、AD分别是∠CBA和∠CAB的平分线,相交于点D,则∠D等于( )
A.90° B.115° C.135° D.150°
4、在△ABC中,∠A∶∠B∶∠C=2∶3∶5,则∠C的度数是( ).
A.60° B.75° C.80° D.90°
5、如图,△ABC和△ABD都是直角三角形,∠ACB=∠ADB=90°,点E为AB的中点,连接CE、CD、DE,若∠ABC+∠DAB=65°,则∠ECD的度数是 .
6、如图,在Rt△ABC中,∠BAC=90°.
(1)若AD是BC上的高,则图中直角的个数是__ ,它们分别是__ __;
(2)若AE为BC边上的中线,BC=12 cm,则AE=______cm,图中∠C相等的角是 ;
(3)∠C=3∠B+10°,则∠EDA=_______.
7、直角三角形斜边上的高与中线分别为8cm和10 cm,则它的面积是_____cm2.
8、如图,△ABC和△ECD都是等腰直角三角形,∠ACB=90°,连接AD、BE.
(1)求证:AD=BE;
(2)BE与AD垂直吗?并说明理由.
【提优特训】
9、若三角形的一个内角等于其他两个内角的差,那么这个三角形是( ).
A.等腰三角形 B.直角三角形 C.等边三角形 D.不能确定
10、如图,Rt△ABC中,∠ACB=90°,将△ACD沿着CD折叠,使点A落在边CB上处,若,则∠ADC=( )
A.45° B.60° C.75° D.105°
11、如图,点是等边三角形ABC内一点,若∠APB︰∠BPC︰∠CPA=5︰9︰10,则以线段PA、PB、PC为边的三角形为 .
12、如图,在△ABC中,AC=BC,∠ACB=90°,直角∠EDF的顶点D是BC的中点,两边DE,FF分别交AC,BC于点E,F,有以下结论:①CE=BF;②△EDF是等腰直角三角形;③EF=CD;④S四边形CFDE=S△ABC.上述结论中一定正确的个数是 (填上正确的序号即可).
13、在△ABC中,∠B=∠C,D、E分别是BC、AB的中点,AC=12,BC=6,则△BDE的周长是 .
14、如图,在△ABC中,点D在BC上(点D不与B、C重合),则的取值范围是 .
15、在△ABC中,∠ACB=90°,在AB上截取AE=AC,BD=BC,
求∠DCE的度数.
16、如图,以△ABC的边AB和AC,向外作等腰直角三角形△ABE和ACF,连接EF,AD是△ABC的高,延长DA交EF于点G,求证:点G是EF的中点.
17.如图,在△ABC中,AB=AC,∠A=90°,CD平分∠ACB,E在AC上,且AE=AD,EF⊥CD交BC于点F,交CD于点O.求证:BF=2AD.
【中考链接】
18、2018扬州7.在中,,于,平分交于,则下列结论一定成立的是( )
A. B. C. D.
19、2018淄博11.(4分)如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4 B.6 C. D.8
20、2017武汉10.如图,在Rt△ABC中,∠C=90°,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A.4 B.5 C. 6 D.7
【答案】C
考点:画等腰三角形.
解答:如图①以B为圆心,BC的长为半径画弧,交AB于点D,△BCD就是等腰三角形;
如图②以A为圆心,AC的长为半径画弧,交AB于点E,△ACE就是等腰三角形;
如图③以C为圆心,BC的长为半径画弧,交AC于点F,△BCF就是等腰三角形;
如图④作AC的垂直平分线交AB于点H,△ACH就是等腰三角形;
如图⑤作AB的垂直平分线交AC于点G,△AGB就是等腰三角形;
如图⑥作BC的垂直平分线交AB于点I,△BCI就是等腰三角形.
参考答案
1、C 2、B 3、C 4、D 5、65° 6、(1)3个,∠BAC 、∠BDA、∠CDA;(2)6cm,∠EAC、∠BAD; (3)50° 7、80 9、B 10、C 11、直角三角形 12、①、②、④ 13、15
14、 18、C 19、B 20、C
8、证明:(1)△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,
AC=BC,DC=EC
在△ACD和△BCE中,
∵
∴△ACD≌△BCE(SAS).
∴AD=BE(全等三角形对应边相等).
(2)BE与AD垂直.理由如下:
由(1)△ACD≌△BCE,
∴∠ADC=∠BEC(全等三角形对应角相等).
在△BCE中,∠ACB=90°,
∠EBC+∠BEC=90°,
∠EBC+∠ADC=90°.
BE⊥AD.
15、证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵AC=AE,
∴∠ACE=∠AEC,
∵∠ACE=∠1+∠DCE,∠AEC=∠2+∠B,
∴∠1+∠DCE=∠2+∠B①.
∵BD=BC,
同理∠2+∠DCE =∠1+∠A②.
由①+②,∠1+∠DCE+∠2+∠DCE =∠2+∠B+∠1+∠A.
得2∠DCE=∠A+∠B.
∴∠DCE==45°.
16、证明:过点E作EM⊥DG的延长线于M,过点F作FN⊥DG于N.
∴∠EMA=∠FNG=90°(辅助线的作法)
∵△ABE是等腰直角三角形,
∴∠BAE=90°,AB=AE.
∴∠BAD+∠EAM=90°.
∵AD是△ABC的高,
∴∠DBA+∠BAD=90°.
∴∠DBA=∠MAE.
在△ABD和△EAM中,
∵
∴△ABD≌△EAM(AAS).
∴AD=EM(全等三角形对应边相等).
同理 △ACD≌△FAN.
∴AD=FN
∴EM=FN
在△EMG和△FNG中,
∵
∴△EMG≌△FNG(AAS).
∴EG=FG(全等三角形对应边相等).
∴点G是EF的中点.
17 、证明:连结DF,过点D作DG⊥BC于点G.
∵∠A=90°,AD=AE,AB=AC,
∴∠ADE=∠AED=45°,
∠B=∠ACB=45°,
∴∠ADE=∠B,∴DE∥BC,
∴∠EDC=∠BCD.
∵CD平分∠ACB,
∴∠BCD=∠ACD,
∴∠EDC=∠ACD,∴DE=EC.
∵EF⊥CD,∴EF垂直平分CD.
∴FD=FC,∴∠FDC=∠FCD.
∴∠FDC=∠ACD,∴DF∥AC.
∴∠DFB=∠ACB=45°.
∴∠B=∠BFD=45°,∴BD=DF,∠BDF=90°,
∴△DBF为等腰直角三角形.
∵DG⊥BF,∴DG为斜边BF上的中线,
∴DG=BF.
又∵CD平分∠ACB,∠A=∠DGC=90°,
∴AD=DG.
∴AD=BF,即BF=2AD.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
