第2章 简单事件的概率单元测试卷B(含解析)
文档属性
| 名称 | 第2章 简单事件的概率单元测试卷B(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-07 00:00:00 | ||
图片预览




文档简介
第二章简单事件的概率单元测试卷B
一.选择题(共10小题,3*10=30)
1.某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线图,则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.掷一枚质地均匀的正六面体骰子,向上一面的点数是4
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌,抽中红桃
D.抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面仍朝上
2.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外都相同,其中有5个红球,4个蓝球.若随机摸出一个蓝球的概率为,则随机摸出一个黄球的概率为( )
A. B. C. D.
3.口袋里有除颜色不同其它都相同的红、黄、白三种颜色小球20个,摸到红球的概率是,摸到篮球的概率是,则袋子里有白球( )
A.10个 B.4个 C.5个 D.6个
4.在一个不透明的袋中装有10个只有颜色不同的球,其中5个红球、3个黄球和2个白球.从袋中任意摸出一个球,是白球的概率为( )
A. B. C. D.
5.某学校组织知识竞赛,共设20道试题,其中有关中国优秀传统文化试题10道,实践应用题4道,创新能力题6道.小捷从中任选一道试题作答,他选中创新能力试题的概率是( )
A. B. C. D.
6.掷一个骰子时,观察上面的点数,点数为奇数的概率是( )
A. B. C. D.
7.盒子中装有7个红球,3个黄球和2个篮球,每个球除颜色外没有其他的区别,从中任意摸出一个球,这个球是红球的概率是( )
A. B. C. D.
8.在边长为1的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为1的概率为( )
A. B. C. D.
9.已知下列命题:①对顶角相等;②若a>b>0,则<;③对角线相等且互相垂直的四边形是正方形;④抛物线y=x2﹣2x与坐标轴有3个不同交点;⑤边长相等的多边形内角都相等.从中任选一个命题是真命题的概率为( )
A. B. C. D.
10.如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )
A. B. C. D.
二.填空题(共8小题,3*8=24)
11.一组线段,长度分别为1,2,2,3任取三张,能组成等腰三角形的概率是
12.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组有解的概率为 .
13.某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中一个餐厅用餐,则甲、乙、丙三人中至少有一人在B餐厅用餐的概率是 .
14.为了知道一块不规则的封闭图形的面积,小聪在封闭的图形内画了一个边长为1m的正方形,在不远处向封闭图形内任意投掷石子,且记录如下,则封闭图形的面积为 m2.
掷石子次数
50
100
150
200
300
石子落在正方形内(含边上)
29
61
91
118
178
落在正方形内(含边上)的频率
0.580
0.610
0.607
0.590
0.593
15.从3,﹣1,0,1,﹣2这五个数中任意取出一个数记作b,则既能使函数y=(b2﹣4)x的图象经过第二、第四象限,又能使关于x的一元二次方程x2﹣bx+b+1=0的根的判别式小于零的概率为 .
16.初一(5)班有学生37人,其中4个或4个以上学生在同一个月出生的可能性用百分数表示为 %.
17.已知函数y=(2k﹣1)x+4(k为常数),若从﹣3≤k≤3中任取k值,则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为 .
18.在一个不透明的盒子里装有5个分别写有数字﹣2,﹣1,0,1,2的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,将该小球上的数字作为a的值,将该数字加2作为b的值,则(a,b)使得关于x的不等式组恰好有两个整数解的概率是 .
三.解答题(共7小题,66分)
19.(8分)一个不透明口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色处没有任何其他区别现.从中任意摸出一个球.
(1)计算摸到的是绿球的概率.
(2)如果要使摸到绿球的概率为,需要在这个口袋中再放入多少个绿球?
20.(8分)一个不透明的袋中装有5个黄球,13个黑球和22和红球,这些球除颜色外其它都相同
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率为,则取出了多少个黑球?
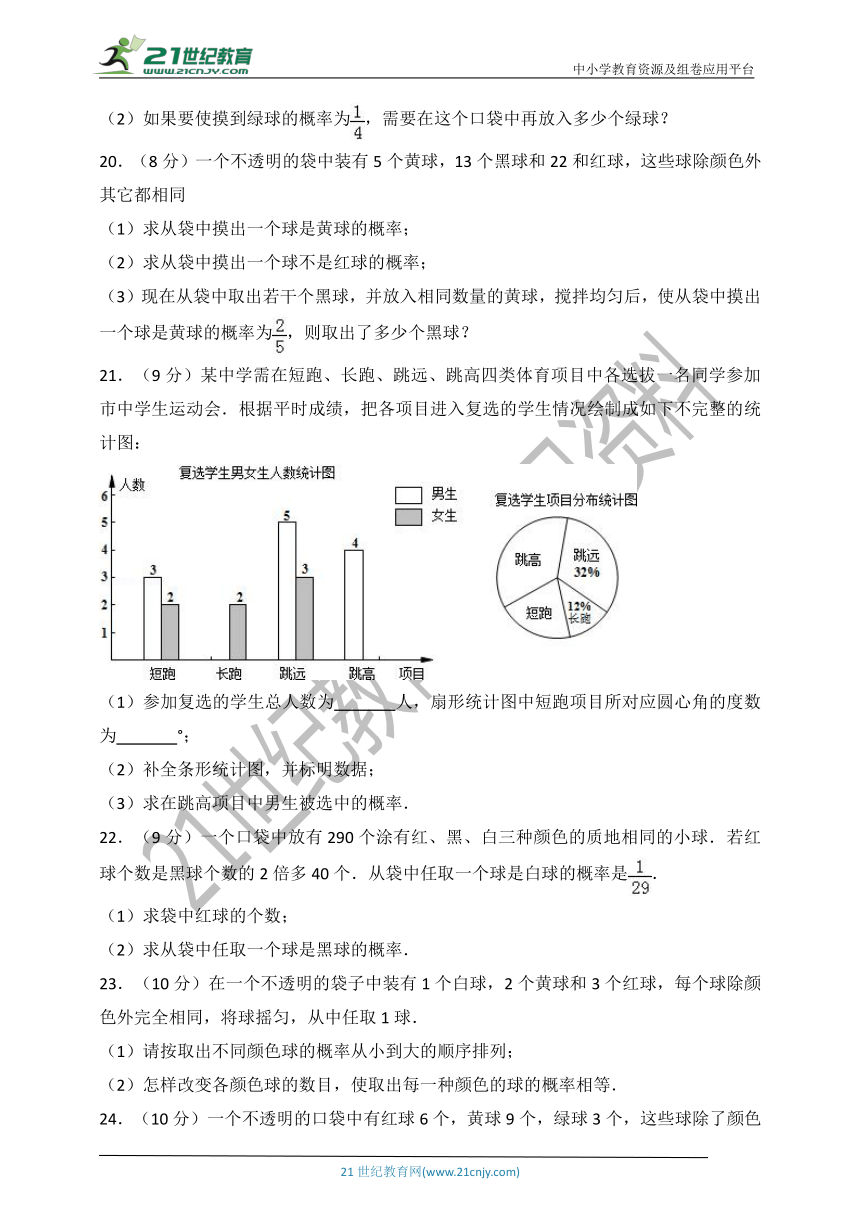
21.(9分)某中学需在短跑、长跑、跳远、跳高四类体育项目中各选拔一名同学参加市中学生运动会.根据平时成绩,把各项目进入复选的学生情况绘制成如下不完整的统计图:
(1)参加复选的学生总人数为 人,扇形统计图中短跑项目所对应圆心角的度数为 °;
(2)补全条形统计图,并标明数据;
(3)求在跳高项目中男生被选中的概率.
22.(9分)一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
23.(10分)在一个不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外完全相同,将球摇匀,从中任取1球.
(1)请按取出不同颜色球的概率从小到大的顺序排列;
(2)怎样改变各颜色球的数目,使取出每一种颜色的球的概率相等.
24.(10分)一个不透明的口袋中有红球6个,黄球9个,绿球3个,这些球除了颜色外没有其他任何区别,从中任间摸出一个球.
(1)求摸到绿球的概率;
(2)如果要使摸到绿球的概率为,需要在口袋中拿出多少个黄球?
25.(12分)有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)可能性最大和最小的事件分别是哪个?(填写序号)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列: .
参考答案与试题解析
1.解:A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”频率约为,不符合题意;
B、掷一枚质地均匀的正六面体骰子,向上一面的点数是4的频率约为≈0.17,符合题意;
C、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌,抽中红桃的频率为=0.25,不符合题意;
D、抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面仍朝上的频率约为=0.2,不符合题意;
故选:B.
2.解:设袋子中黄球有x个,
根据题意,得:=,
解得:x=3,
即袋中黄球有3个,
所以随机摸出一个黄球的概率为=,
故选:A.
3.解:因为摸到红球的概率是,摸到蓝球的概率是,
所以红球的个数为×20=4,蓝球的个数为×20=10,
所以袋子里有白球有20﹣4﹣10=6,
故选:D.
4.解:∵袋子中共有10个小球,其中白球有2个,
∴摸出一个球是白球的概率是=,
故选:D.
5.解:∵共设有20道试题,其中创新能力试题6道,
∴小捷选中创新能力试题的概率是=,
故选:B.
6.解:掷一个骰子,观察向上的面的点数,有6种情况,则点数为奇数有3种情况,
故点数为奇数的概率为=,
故选:A.
7.解:∵有7个红球,3个黄球,2个蓝球,共12个,
∴摸到红球的概率为,
故选:C.
8.解:可以找到4个恰好能使△ABC的面积为1的点,
则概率为:4÷16=.
故选:C.
9.解:①对顶角相等,故此选项正确;
②若a>b>0,则<,故此选项正确;
③对角线相等且互相垂直平分的四边形是正方形,故此选项错误;
④抛物线y=x2﹣2x与坐标轴有2个不同交点,故此选项错误;
⑤边长相等的多边形内角不一定都相等,故此选项错误;
从中任选一个命题是真命题的概率为:.
故选:B.
10.解:∵由图可知,当1号到达时,停留的日子为1、2、3、4号,此时为(40,62,150,110),2天空气质量均为优良;
当2号到达时,停留的日子为2、3、4、5号,此时为(62,150,110,220),1天空气质量为优良;
当3号到达时,停留的日子为3、4、5、6号,此时为(150,110,220,141),0天空气质量为优良;
当4号到达时,停留的日子为4、5、6、7号,此时为(110,220,141,82),1天空气质量为优良;
当5号到达时,停留的日子为5、6、7、8号,此时为(221,141,82,199),1天空气质量为优;
当6号到达时,停留的日子为6、7、8、9号,此时为(141,82,199,51),2天空气质量为优良;
当7号到达时,停留的日子为7、8、9、10号,此时为(82,199,51,133),2天空气质量为优;
∴此人在该市停留期间恰好有两天空气质量优良的概率=.
故选:B.
11.解:P(组成等腰三角形)=.
故本题答案为:.
12.解:,
由①得:x≥3,
由②得:x<,
∵关于x的不等式组有解,
∴>3,
解得:a>5,
∴使关于x的不等式组有解的概率为:.
故答案为:.
13.解:某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中一个餐厅用餐,共8种情况;甲、乙、丙三人都不在B餐厅,即都在A餐厅用餐的只有1种情况,至少有一人在B餐厅用餐有7种情况,故其概率为.
14.解:根据统计表,可得石子落在正方形内的概率约为0.593,
设封闭图形的面积为x,
则有=0.593,
解得x≈1.7.
∴封闭图形的面积为1.7,
故答案为:1.7.
15.解:∵函数y=(b2﹣4)x的图象经过第二、四象限,
∴b2﹣4<0,
解得:﹣2<b<2
∵关于x的一元二次方程x2﹣bx+b+1=0的根的判别式小于零,
∴(﹣b)2﹣4(b+1)<0,
∴2﹣2<b<2+2,
∴使函数的图象经过第二、四象限,且使方程的根的判别式小于零的b的值有为0、1,
∴此事件的概率为,
故答案为:.
16.解:∵一年有12个月,把37个平均分到12个月中=3…1,
∴剩下那一个无论怎么放都使那个月里超过4人.
故答案为:100%.
17.解:当2k﹣1>0时,
解得:k>,则<k≤3时,y随x增加而增加,
故﹣3≤k<时,y随x增加而减小,
则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为:=.
故答案为:.
18.解:根据题意得:(a,b)的等可能结果有:(﹣2,0),(﹣1,1),(0,2),(1,3),(2,4)共5种;
∵,
解①得:x≥,
解②得:x<b,
∴≤x<b,
∴(a,b)使得关于x的不等式组恰好有两个整数解的有(0,2)与(1,3),
∴(a,b)使得关于x的不等式组恰好有两个整数解的概率是.
故答案为:.
19.解:(1)根据题意分析可得:口袋中装有红球6个,黄球9个,绿球3个,共18个球,故P(摸到绿球)=;
(2)设需要在这个口袋中再放入x个绿球,得:,
解得:x=2.
所以需要在这个口袋中再放入2个绿球.
20.解:(1)因为共有5+13+22=40个小球,
所以从袋中摸出一个球是黄球的概率为=;
(2)从袋中摸出一个球不是红球的概率为=;
(3)设取出了x个黑球,
根据题意,得:=,
解得:x=11,
答:取出了11个黑球.
21.解:(1)由扇形统计图和条形统计图可得:
参加复选的学生总人数为:(5+3)÷32%=25(人);
扇形统计图中短跑项目所对应圆心角的度数为:×360°=72°.
故答案为:25,72;
(2)长跑项目的男生人数为:25×12%﹣2=1,
跳高项目的女生人数为:25﹣3﹣2﹣1﹣2﹣5﹣3﹣4=5.
如下图:
(3)∵复选中的跳高总人数为9人,
跳高项目中的男生共有4人,
∴跳高项目中男生被选中的概率=.
22.解:(1)290×=10(个),
290﹣10=280(个),
(280﹣40)÷(2+1)=80(个),
280﹣80=200(个).
故袋中红球的个数是200个;
(2)80÷290=.
答:从袋中任取一个球是黑球的概率是.
23.解:(1)根据题意,袋子中共6个球,其中有1个白球,2个黄球和3个红球,故将球摇匀,从中任取1球,
①恰好取出白球的可能性为 ,
②恰好取出黄球的可能性为 =,
③恰好取出红球的可能性为 =,
故这些事件按发生的可能性从小到大的顺序排列是①<②<③.
(2)将其中一个红球变成白球,可使取出每种颜色的球的概率都相等.此题答案不唯一.
24.解:(1)由题意可得,
摸到绿球的概率是:,
即摸到绿球的概率是;
(2)设需要在口袋中拿出x个黄球,
,
解得,x=6,
答:需要在口袋中拿出6个黄球.
25.解:∵共3红2黄1绿相等的六部分,
∴①指针指向红色的概率为=;
②指针指向绿色的概率为;
③指针指向黄色的概率为=;
④指针不指向黄色为,
(1)可能性最大的是④,最小的是②;
(2)由题意得:②<③<①<④,
故答案为:②<③<①<④.
一.选择题(共10小题,3*10=30)
1.某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线图,则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.掷一枚质地均匀的正六面体骰子,向上一面的点数是4
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌,抽中红桃
D.抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面仍朝上
2.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外都相同,其中有5个红球,4个蓝球.若随机摸出一个蓝球的概率为,则随机摸出一个黄球的概率为( )
A. B. C. D.
3.口袋里有除颜色不同其它都相同的红、黄、白三种颜色小球20个,摸到红球的概率是,摸到篮球的概率是,则袋子里有白球( )
A.10个 B.4个 C.5个 D.6个
4.在一个不透明的袋中装有10个只有颜色不同的球,其中5个红球、3个黄球和2个白球.从袋中任意摸出一个球,是白球的概率为( )
A. B. C. D.
5.某学校组织知识竞赛,共设20道试题,其中有关中国优秀传统文化试题10道,实践应用题4道,创新能力题6道.小捷从中任选一道试题作答,他选中创新能力试题的概率是( )
A. B. C. D.
6.掷一个骰子时,观察上面的点数,点数为奇数的概率是( )
A. B. C. D.
7.盒子中装有7个红球,3个黄球和2个篮球,每个球除颜色外没有其他的区别,从中任意摸出一个球,这个球是红球的概率是( )
A. B. C. D.
8.在边长为1的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为1的概率为( )
A. B. C. D.
9.已知下列命题:①对顶角相等;②若a>b>0,则<;③对角线相等且互相垂直的四边形是正方形;④抛物线y=x2﹣2x与坐标轴有3个不同交点;⑤边长相等的多边形内角都相等.从中任选一个命题是真命题的概率为( )
A. B. C. D.
10.如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )
A. B. C. D.
二.填空题(共8小题,3*8=24)
11.一组线段,长度分别为1,2,2,3任取三张,能组成等腰三角形的概率是
12.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组有解的概率为 .
13.某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中一个餐厅用餐,则甲、乙、丙三人中至少有一人在B餐厅用餐的概率是 .
14.为了知道一块不规则的封闭图形的面积,小聪在封闭的图形内画了一个边长为1m的正方形,在不远处向封闭图形内任意投掷石子,且记录如下,则封闭图形的面积为 m2.
掷石子次数
50
100
150
200
300
石子落在正方形内(含边上)
29
61
91
118
178
落在正方形内(含边上)的频率
0.580
0.610
0.607
0.590
0.593
15.从3,﹣1,0,1,﹣2这五个数中任意取出一个数记作b,则既能使函数y=(b2﹣4)x的图象经过第二、第四象限,又能使关于x的一元二次方程x2﹣bx+b+1=0的根的判别式小于零的概率为 .
16.初一(5)班有学生37人,其中4个或4个以上学生在同一个月出生的可能性用百分数表示为 %.
17.已知函数y=(2k﹣1)x+4(k为常数),若从﹣3≤k≤3中任取k值,则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为 .
18.在一个不透明的盒子里装有5个分别写有数字﹣2,﹣1,0,1,2的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,将该小球上的数字作为a的值,将该数字加2作为b的值,则(a,b)使得关于x的不等式组恰好有两个整数解的概率是 .
三.解答题(共7小题,66分)
19.(8分)一个不透明口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色处没有任何其他区别现.从中任意摸出一个球.
(1)计算摸到的是绿球的概率.
(2)如果要使摸到绿球的概率为,需要在这个口袋中再放入多少个绿球?
20.(8分)一个不透明的袋中装有5个黄球,13个黑球和22和红球,这些球除颜色外其它都相同
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率为,则取出了多少个黑球?
21.(9分)某中学需在短跑、长跑、跳远、跳高四类体育项目中各选拔一名同学参加市中学生运动会.根据平时成绩,把各项目进入复选的学生情况绘制成如下不完整的统计图:
(1)参加复选的学生总人数为 人,扇形统计图中短跑项目所对应圆心角的度数为 °;
(2)补全条形统计图,并标明数据;
(3)求在跳高项目中男生被选中的概率.
22.(9分)一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
23.(10分)在一个不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外完全相同,将球摇匀,从中任取1球.
(1)请按取出不同颜色球的概率从小到大的顺序排列;
(2)怎样改变各颜色球的数目,使取出每一种颜色的球的概率相等.
24.(10分)一个不透明的口袋中有红球6个,黄球9个,绿球3个,这些球除了颜色外没有其他任何区别,从中任间摸出一个球.
(1)求摸到绿球的概率;
(2)如果要使摸到绿球的概率为,需要在口袋中拿出多少个黄球?
25.(12分)有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)可能性最大和最小的事件分别是哪个?(填写序号)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列: .
参考答案与试题解析
1.解:A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”频率约为,不符合题意;
B、掷一枚质地均匀的正六面体骰子,向上一面的点数是4的频率约为≈0.17,符合题意;
C、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌,抽中红桃的频率为=0.25,不符合题意;
D、抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面仍朝上的频率约为=0.2,不符合题意;
故选:B.
2.解:设袋子中黄球有x个,
根据题意,得:=,
解得:x=3,
即袋中黄球有3个,
所以随机摸出一个黄球的概率为=,
故选:A.
3.解:因为摸到红球的概率是,摸到蓝球的概率是,
所以红球的个数为×20=4,蓝球的个数为×20=10,
所以袋子里有白球有20﹣4﹣10=6,
故选:D.
4.解:∵袋子中共有10个小球,其中白球有2个,
∴摸出一个球是白球的概率是=,
故选:D.
5.解:∵共设有20道试题,其中创新能力试题6道,
∴小捷选中创新能力试题的概率是=,
故选:B.
6.解:掷一个骰子,观察向上的面的点数,有6种情况,则点数为奇数有3种情况,
故点数为奇数的概率为=,
故选:A.
7.解:∵有7个红球,3个黄球,2个蓝球,共12个,
∴摸到红球的概率为,
故选:C.
8.解:可以找到4个恰好能使△ABC的面积为1的点,
则概率为:4÷16=.
故选:C.
9.解:①对顶角相等,故此选项正确;
②若a>b>0,则<,故此选项正确;
③对角线相等且互相垂直平分的四边形是正方形,故此选项错误;
④抛物线y=x2﹣2x与坐标轴有2个不同交点,故此选项错误;
⑤边长相等的多边形内角不一定都相等,故此选项错误;
从中任选一个命题是真命题的概率为:.
故选:B.
10.解:∵由图可知,当1号到达时,停留的日子为1、2、3、4号,此时为(40,62,150,110),2天空气质量均为优良;
当2号到达时,停留的日子为2、3、4、5号,此时为(62,150,110,220),1天空气质量为优良;
当3号到达时,停留的日子为3、4、5、6号,此时为(150,110,220,141),0天空气质量为优良;
当4号到达时,停留的日子为4、5、6、7号,此时为(110,220,141,82),1天空气质量为优良;
当5号到达时,停留的日子为5、6、7、8号,此时为(221,141,82,199),1天空气质量为优;
当6号到达时,停留的日子为6、7、8、9号,此时为(141,82,199,51),2天空气质量为优良;
当7号到达时,停留的日子为7、8、9、10号,此时为(82,199,51,133),2天空气质量为优;
∴此人在该市停留期间恰好有两天空气质量优良的概率=.
故选:B.
11.解:P(组成等腰三角形)=.
故本题答案为:.
12.解:,
由①得:x≥3,
由②得:x<,
∵关于x的不等式组有解,
∴>3,
解得:a>5,
∴使关于x的不等式组有解的概率为:.
故答案为:.
13.解:某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中一个餐厅用餐,共8种情况;甲、乙、丙三人都不在B餐厅,即都在A餐厅用餐的只有1种情况,至少有一人在B餐厅用餐有7种情况,故其概率为.
14.解:根据统计表,可得石子落在正方形内的概率约为0.593,
设封闭图形的面积为x,
则有=0.593,
解得x≈1.7.
∴封闭图形的面积为1.7,
故答案为:1.7.
15.解:∵函数y=(b2﹣4)x的图象经过第二、四象限,
∴b2﹣4<0,
解得:﹣2<b<2
∵关于x的一元二次方程x2﹣bx+b+1=0的根的判别式小于零,
∴(﹣b)2﹣4(b+1)<0,
∴2﹣2<b<2+2,
∴使函数的图象经过第二、四象限,且使方程的根的判别式小于零的b的值有为0、1,
∴此事件的概率为,
故答案为:.
16.解:∵一年有12个月,把37个平均分到12个月中=3…1,
∴剩下那一个无论怎么放都使那个月里超过4人.
故答案为:100%.
17.解:当2k﹣1>0时,
解得:k>,则<k≤3时,y随x增加而增加,
故﹣3≤k<时,y随x增加而减小,
则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为:=.
故答案为:.
18.解:根据题意得:(a,b)的等可能结果有:(﹣2,0),(﹣1,1),(0,2),(1,3),(2,4)共5种;
∵,
解①得:x≥,
解②得:x<b,
∴≤x<b,
∴(a,b)使得关于x的不等式组恰好有两个整数解的有(0,2)与(1,3),
∴(a,b)使得关于x的不等式组恰好有两个整数解的概率是.
故答案为:.
19.解:(1)根据题意分析可得:口袋中装有红球6个,黄球9个,绿球3个,共18个球,故P(摸到绿球)=;
(2)设需要在这个口袋中再放入x个绿球,得:,
解得:x=2.
所以需要在这个口袋中再放入2个绿球.
20.解:(1)因为共有5+13+22=40个小球,
所以从袋中摸出一个球是黄球的概率为=;
(2)从袋中摸出一个球不是红球的概率为=;
(3)设取出了x个黑球,
根据题意,得:=,
解得:x=11,
答:取出了11个黑球.
21.解:(1)由扇形统计图和条形统计图可得:
参加复选的学生总人数为:(5+3)÷32%=25(人);
扇形统计图中短跑项目所对应圆心角的度数为:×360°=72°.
故答案为:25,72;
(2)长跑项目的男生人数为:25×12%﹣2=1,
跳高项目的女生人数为:25﹣3﹣2﹣1﹣2﹣5﹣3﹣4=5.
如下图:
(3)∵复选中的跳高总人数为9人,
跳高项目中的男生共有4人,
∴跳高项目中男生被选中的概率=.
22.解:(1)290×=10(个),
290﹣10=280(个),
(280﹣40)÷(2+1)=80(个),
280﹣80=200(个).
故袋中红球的个数是200个;
(2)80÷290=.
答:从袋中任取一个球是黑球的概率是.
23.解:(1)根据题意,袋子中共6个球,其中有1个白球,2个黄球和3个红球,故将球摇匀,从中任取1球,
①恰好取出白球的可能性为 ,
②恰好取出黄球的可能性为 =,
③恰好取出红球的可能性为 =,
故这些事件按发生的可能性从小到大的顺序排列是①<②<③.
(2)将其中一个红球变成白球,可使取出每种颜色的球的概率都相等.此题答案不唯一.
24.解:(1)由题意可得,
摸到绿球的概率是:,
即摸到绿球的概率是;
(2)设需要在口袋中拿出x个黄球,
,
解得,x=6,
答:需要在口袋中拿出6个黄球.
25.解:∵共3红2黄1绿相等的六部分,
∴①指针指向红色的概率为=;
②指针指向绿色的概率为;
③指针指向黄色的概率为=;
④指针不指向黄色为,
(1)可能性最大的是④,最小的是②;
(2)由题意得:②<③<①<④,
故答案为:②<③<①<④.
同课章节目录
