第1章 三角形的初步知识单元检测题2(含解析)
文档属性
| 名称 | 第1章 三角形的初步知识单元检测题2(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 323.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-08 17:01:21 | ||
图片预览

文档简介
第1章三角形的初步知识检测题2
(时间:100分钟 满分:120分)
题号
1
2
3
4
5
6
7
8
9
10
答案
一、选择题(共10小题 每3分 共30分)
1、若三角形的三边分别为5cm,8cm,()cm,则a的取值范围是( ).
A.3 2、把命题“等底等高的三角形的面积相等”改写成“如果……那么……”的形式,正确的是( )
A.如果等底等高,那么面积相等
B. 如果等底等高,那么三角形面积相等
C. 如果三角形等底等高,那么面积相等
D. 如果两个三角形有一边和这边上的高相等,那么这两个三角形的面积相等
3、有一个三角形的三个内角都不相等,其中最小的角为47°,这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4、利用尺规作图,作不出唯一三角形是(?????? )
A.已知三边???????B.已知两边及其中一边的对角 C.已知两角及夹边????D.已知两边及夹角
5、如图,在△ABC中,点D在边BC上,点E、G分别是BF、AC的中点,若BC=3DC,△ABC的面积为12,则的值是( ).
A. B.1 C.2 D.3
6、下列命题中是真命题的是( )
A.只有无限循环小数才是有理数 B.只有开方开不尽的数才是无理数
C.只有正数才有平方根 D.只有实数才能与数轴上的点是一一对应的关系
7、如图,直线、,被直线所截,且∥,过上的点A作AB⊥于点B,其中,则下列一定正确的是( )
A. B. C. D.
8、在,∠A=43°,∠B=65°,∠ ,∠,且,那么这两个三角形( )
A.不一定全等 B.一定不全等 C.一定全等 D.以上都不对
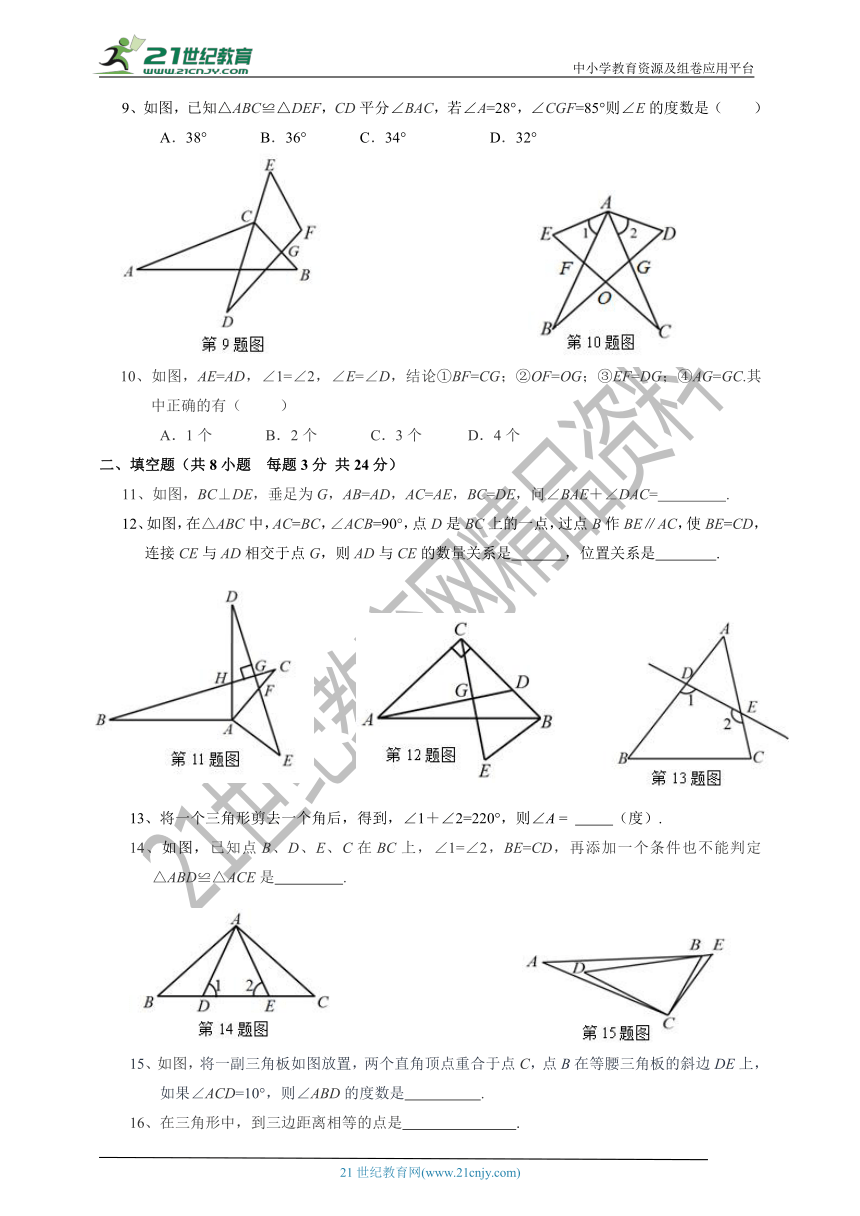
9、如图,已知△ABC≌△DEF,CD平分∠BAC,若∠A=28°,∠CGF=85°则∠E的度数是( )
A.38° B.36° C.34° D.32°
10、如图,AE=AD,∠1=∠2,∠E=∠D,结论①BF=CG;②OF=OG;③EF=DG;④AG=GC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题 每题3分 共24分)
11、如图,BC⊥DE,垂足为G,AB=AD,AC=AE,BC=DE,问∠BAE+∠DAC= .
12、如图,在△ABC中,AC=BC,∠ACB=90°,点D是BC上的一点,过点B作BE∥AC,使BE=CD,
连接CE与AD相交于点G,则AD与CE的数量关系是 ,位置关系是 .
13、将一个三角形剪去一个角后,得到,∠1+∠2=220°,则∠A = (度).
14、如图,已知点B、D、E、C在BC上,∠1=∠2,BE=CD,再添加一个条件也不能判定△ABD≌△ACE是 .
15、如图,将一副三角板如图放置,两个直角顶点重合于点C,点B在等腰三角板的斜边DE上,如果∠ACD=10°,则∠ABD的度数是 .
16、在三角形中,到三边距离相等的点是 .
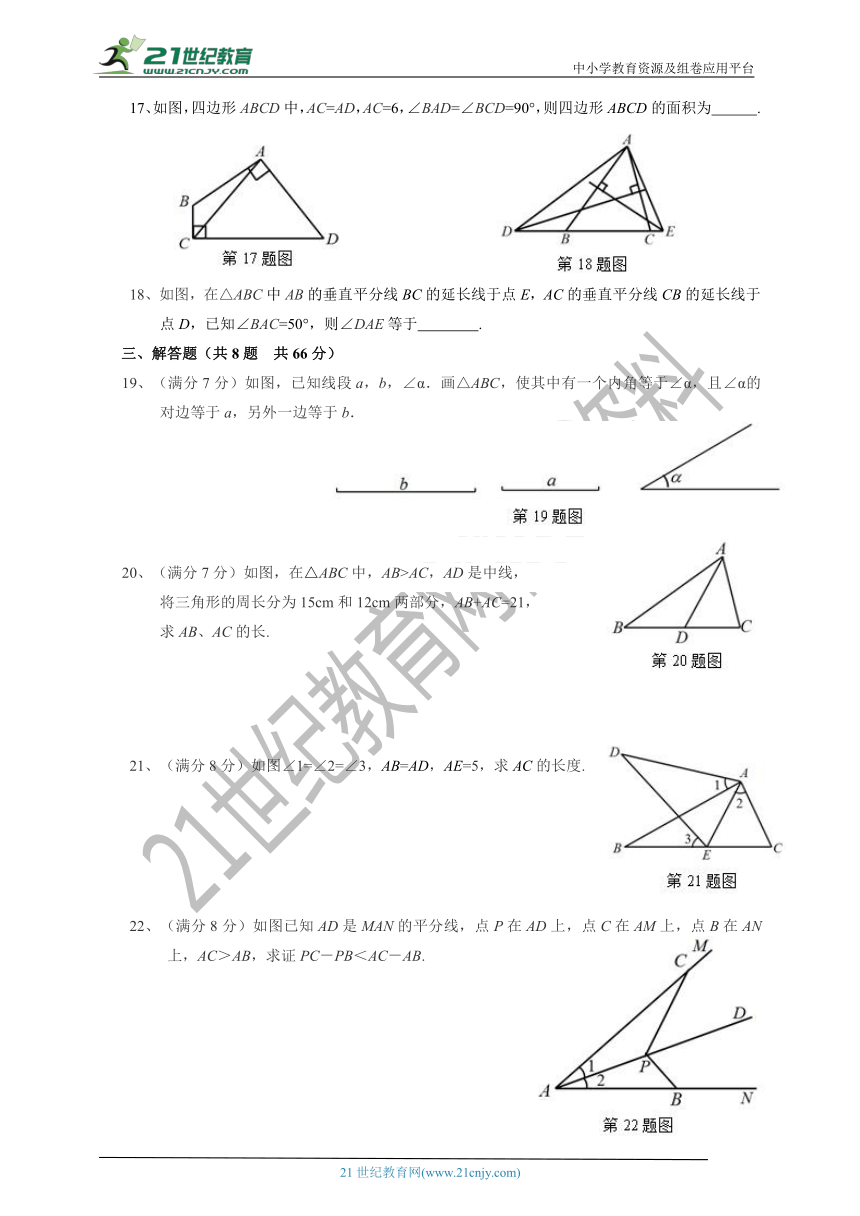
17、如图,四边形ABCD中,AC=AD,AC=6,∠BAD=∠BCD=90°,则四边形ABCD的面积为 .
18、如图,在△ABC中AB的垂直平分线BC的延长线于点E,AC的垂直平分线CB的延长线于
点D,已知∠BAC=50°,则∠DAE等于 .
三、解答题(共8题 共66分)
19、(满分7分)如图,已知线段a,b,∠α.画△ABC,使其中有一个内角等于∠α,且∠α的对边等于a,另外一边等于b.
20、(满分7分)如图,在△ABC中,AB>AC,AD是中线,
将三角形的周长分为15cm和12cm两部分,AB+AC=21,
求AB、AC的长.
21、(满分8分)如图∠1=∠2=∠3,AB=AD,AE=5,求AC的长度.
22、(满分8分)如图已知AD是MAN的平分线,点P在AD上,点C在AM上,点B在AN上,AC>AB,求证PC-PB<AC-AB.
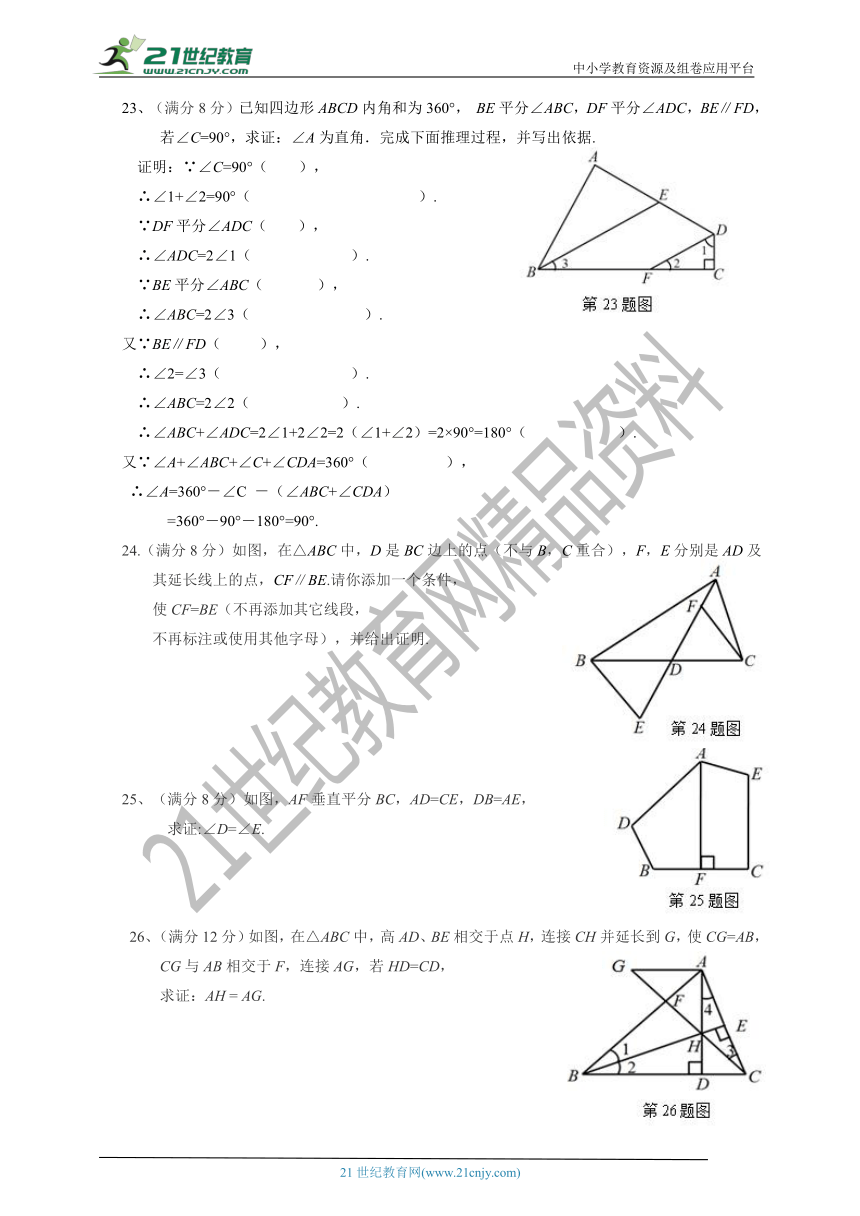
23、(满分8分)已知四边形ABCD内角和为360°, BE平分∠ABC,DF平分∠ADC,BE∥FD,若∠C=90°,求证:∠A为直角.完成下面推理过程,并写出依据.
证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC( ),
∴∠ADC=2∠1( ).
∵BE平分∠ABC( ),
∴∠ABC=2∠3( ).
又∵BE∥FD( ),
∴∠2=∠3( ).
∴∠ABC=2∠2( ).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°( ).
又∵∠A+∠ABC+∠C+∠CDA=360°( ),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°.
24.(满分8分)如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,
使CF=BE(不再添加其它线段,
不再标注或使用其他字母),并给出证明.
25、(满分8分)如图,AF垂直平分BC,AD=CE,DB=AE,
求证:∠D=∠E.
26、(满分12分)如图,在△ABC中,高AD、BE相交于点H,连接CH并延长到G,使CG=AB,CG与AB相交于F,连接AG,若HD=CD,
求证:AH = AG.
参考答案
一、选择题(共10小题 每3分 共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
B
D
D
C
A
C
二、填空题(共8小题 每题3分 共24分)
11.90° 12.AD=CE ,AD⊥CE 13.40° 14.AB=AC 15.5° 16.三角形三条角平分线的交点
17.18 18.80°
三、解答题(共8题 共66分)
19.作法:1. ∠MAN=∠α,
2.在BM上截取BA= b,
3.以点A为圆心,a为半径画弧,交BN于点、,
、均为符合条件的所求三角形.
20.题解答:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长=AB+BD+AD,
??△ACD的周长=AC+CD+AD =AC+BD+AD,
∴△ABD的周长-△ACD的周长=AB-AC=3.
又∵AB+AC=21,
解方程组,得,AB=12,AC=9
答:AB和AC的长分别为12cm和9cm.
21.解:∵∠1=∠3(已知),
∠4=∠5(对顶角相等),
∴∠D=∠B(三角形内角和定理).
∵∠1=∠2(已知),
∴∠1+∠BAE=∠2+∠BAE(等量加等量和相等),
∴即∠DAE=∠BAC.
在△DAE和△BAC中,
∴△DAE≌△BAC(ASA).
∴AC=AE=(全等三角形对应边相等).
22.证明:在AM上截取AE=AB,连接EP,
在△AEP和△ABP中,
∴△AEP≌△ABP(SAS).
∴PE=PB(全等三角形对应边相等).
在△EPC中,
∵PC-PE<EC(三角形三边关系定理)
∴PC-PB<AC-AE(等量代换).
即PC-PB<AC-AB(等量代换).
23证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC(已知 ),
∴∠ADC=2∠1(角平分线定义).
∵BE平分∠ABC(已知 ),
∴∠ABC=2∠3(角平分线定义).
又∵BE∥FD(已知 ),
∴∠2=∠3(两直线平行,同位角相等).
∴∠ABC=2∠2(等量代换).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°(等量代换).
又∵∠A+∠ABC+∠C+∠CDA=360°(已知),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°(等式的性质).
24.解:(1)添加的条件是: BD=CD ;
(2)证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行内错角相等),
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA)
CF=BE(全等三角形对应边相等)
25.证明:连接AB、AC,
∵ AF垂直平分BC(已知),
∴ AB=AC(线段垂直平分线的性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(SSS)
∴∠D=∠E(全等三角形对应角相等).
26.证明:∵AD、BE是△ABC的高(已知),
∴∠BEC=∠ADC=∠ADB= 90°(垂直定义).
∴∠2+∠BCA=90°,∠4+∠BCA =90°(直角三角形两锐角互余).
∴∠2 =∠4(等式的性质).
△BHD和△ACD中,
∴△BHD≌△ACD(AAS).
∴BH=CA(全等三角形对应边相等).
∵H是高AD、BE的交点(已知),
∴CF⊥AB(三角形三条高相交于一点),
∴∠BEA=∠CFA=90°(垂直定义).
∴∠1+∠BAC=90°,∠3+∠BAC =90°(直角三角形两锐角互余).
∴∠1 =∠3(等式的性质).
△ABH和△GCA中,
∴△ABH≌△GCA(SAS).
第1章三角形的初步知识检测题2
(时间:100分钟 满分:120分)
题号
1
2
3
4
5
6
7
8
9
10
答案
一、选择题(共10小题 每3分 共30分)
1、若三角形的三边分别为5cm,8cm,()cm,则a的取值范围是( ).
A.3 2、把命题“等底等高的三角形的面积相等”改写成“如果……那么……”的形式,正确的是( )
A.如果等底等高,那么面积相等
B. 如果等底等高,那么三角形面积相等
C. 如果三角形等底等高,那么面积相等
D. 如果两个三角形有一边和这边上的高相等,那么这两个三角形的面积相等
3、有一个三角形的三个内角都不相等,其中最小的角为47°,这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4、利用尺规作图,作不出唯一三角形是(?????? )
A.已知三边???????B.已知两边及其中一边的对角 C.已知两角及夹边????D.已知两边及夹角
5、如图,在△ABC中,点D在边BC上,点E、G分别是BF、AC的中点,若BC=3DC,△ABC的面积为12,则的值是( ).
A. B.1 C.2 D.3
6、下列命题中是真命题的是( )
A.只有无限循环小数才是有理数 B.只有开方开不尽的数才是无理数
C.只有正数才有平方根 D.只有实数才能与数轴上的点是一一对应的关系
7、如图,直线、,被直线所截,且∥,过上的点A作AB⊥于点B,其中,则下列一定正确的是( )
A. B. C. D.
8、在,∠A=43°,∠B=65°,∠ ,∠,且,那么这两个三角形( )
A.不一定全等 B.一定不全等 C.一定全等 D.以上都不对
9、如图,已知△ABC≌△DEF,CD平分∠BAC,若∠A=28°,∠CGF=85°则∠E的度数是( )
A.38° B.36° C.34° D.32°
10、如图,AE=AD,∠1=∠2,∠E=∠D,结论①BF=CG;②OF=OG;③EF=DG;④AG=GC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题 每题3分 共24分)
11、如图,BC⊥DE,垂足为G,AB=AD,AC=AE,BC=DE,问∠BAE+∠DAC= .
12、如图,在△ABC中,AC=BC,∠ACB=90°,点D是BC上的一点,过点B作BE∥AC,使BE=CD,
连接CE与AD相交于点G,则AD与CE的数量关系是 ,位置关系是 .
13、将一个三角形剪去一个角后,得到,∠1+∠2=220°,则∠A = (度).
14、如图,已知点B、D、E、C在BC上,∠1=∠2,BE=CD,再添加一个条件也不能判定△ABD≌△ACE是 .
15、如图,将一副三角板如图放置,两个直角顶点重合于点C,点B在等腰三角板的斜边DE上,如果∠ACD=10°,则∠ABD的度数是 .
16、在三角形中,到三边距离相等的点是 .
17、如图,四边形ABCD中,AC=AD,AC=6,∠BAD=∠BCD=90°,则四边形ABCD的面积为 .
18、如图,在△ABC中AB的垂直平分线BC的延长线于点E,AC的垂直平分线CB的延长线于
点D,已知∠BAC=50°,则∠DAE等于 .
三、解答题(共8题 共66分)
19、(满分7分)如图,已知线段a,b,∠α.画△ABC,使其中有一个内角等于∠α,且∠α的对边等于a,另外一边等于b.
20、(满分7分)如图,在△ABC中,AB>AC,AD是中线,
将三角形的周长分为15cm和12cm两部分,AB+AC=21,
求AB、AC的长.
21、(满分8分)如图∠1=∠2=∠3,AB=AD,AE=5,求AC的长度.
22、(满分8分)如图已知AD是MAN的平分线,点P在AD上,点C在AM上,点B在AN上,AC>AB,求证PC-PB<AC-AB.
23、(满分8分)已知四边形ABCD内角和为360°, BE平分∠ABC,DF平分∠ADC,BE∥FD,若∠C=90°,求证:∠A为直角.完成下面推理过程,并写出依据.
证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC( ),
∴∠ADC=2∠1( ).
∵BE平分∠ABC( ),
∴∠ABC=2∠3( ).
又∵BE∥FD( ),
∴∠2=∠3( ).
∴∠ABC=2∠2( ).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°( ).
又∵∠A+∠ABC+∠C+∠CDA=360°( ),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°.
24.(满分8分)如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,
使CF=BE(不再添加其它线段,
不再标注或使用其他字母),并给出证明.
25、(满分8分)如图,AF垂直平分BC,AD=CE,DB=AE,
求证:∠D=∠E.
26、(满分12分)如图,在△ABC中,高AD、BE相交于点H,连接CH并延长到G,使CG=AB,CG与AB相交于F,连接AG,若HD=CD,
求证:AH = AG.
参考答案
一、选择题(共10小题 每3分 共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
B
D
D
C
A
C
二、填空题(共8小题 每题3分 共24分)
11.90° 12.AD=CE ,AD⊥CE 13.40° 14.AB=AC 15.5° 16.三角形三条角平分线的交点
17.18 18.80°
三、解答题(共8题 共66分)
19.作法:1. ∠MAN=∠α,
2.在BM上截取BA= b,
3.以点A为圆心,a为半径画弧,交BN于点、,
、均为符合条件的所求三角形.
20.题解答:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长=AB+BD+AD,
??△ACD的周长=AC+CD+AD =AC+BD+AD,
∴△ABD的周长-△ACD的周长=AB-AC=3.
又∵AB+AC=21,
解方程组,得,AB=12,AC=9
答:AB和AC的长分别为12cm和9cm.
21.解:∵∠1=∠3(已知),
∠4=∠5(对顶角相等),
∴∠D=∠B(三角形内角和定理).
∵∠1=∠2(已知),
∴∠1+∠BAE=∠2+∠BAE(等量加等量和相等),
∴即∠DAE=∠BAC.
在△DAE和△BAC中,
∴△DAE≌△BAC(ASA).
∴AC=AE=(全等三角形对应边相等).
22.证明:在AM上截取AE=AB,连接EP,
在△AEP和△ABP中,
∴△AEP≌△ABP(SAS).
∴PE=PB(全等三角形对应边相等).
在△EPC中,
∵PC-PE<EC(三角形三边关系定理)
∴PC-PB<AC-AE(等量代换).
即PC-PB<AC-AB(等量代换).
23证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC(已知 ),
∴∠ADC=2∠1(角平分线定义).
∵BE平分∠ABC(已知 ),
∴∠ABC=2∠3(角平分线定义).
又∵BE∥FD(已知 ),
∴∠2=∠3(两直线平行,同位角相等).
∴∠ABC=2∠2(等量代换).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°(等量代换).
又∵∠A+∠ABC+∠C+∠CDA=360°(已知),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°(等式的性质).
24.解:(1)添加的条件是: BD=CD ;
(2)证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行内错角相等),
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA)
CF=BE(全等三角形对应边相等)
25.证明:连接AB、AC,
∵ AF垂直平分BC(已知),
∴ AB=AC(线段垂直平分线的性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(SSS)
∴∠D=∠E(全等三角形对应角相等).
26.证明:∵AD、BE是△ABC的高(已知),
∴∠BEC=∠ADC=∠ADB= 90°(垂直定义).
∴∠2+∠BCA=90°,∠4+∠BCA =90°(直角三角形两锐角互余).
∴∠2 =∠4(等式的性质).
△BHD和△ACD中,
∴△BHD≌△ACD(AAS).
∴BH=CA(全等三角形对应边相等).
∵H是高AD、BE的交点(已知),
∴CF⊥AB(三角形三条高相交于一点),
∴∠BEA=∠CFA=90°(垂直定义).
∴∠1+∠BAC=90°,∠3+∠BAC =90°(直角三角形两锐角互余).
∴∠1 =∠3(等式的性质).
△ABH和△GCA中,
∴△ABH≌△GCA(SAS).
(时间:100分钟 满分:120分)
题号
1
2
3
4
5
6
7
8
9
10
答案
一、选择题(共10小题 每3分 共30分)
1、若三角形的三边分别为5cm,8cm,()cm,则a的取值范围是( ).
A.3
A.如果等底等高,那么面积相等
B. 如果等底等高,那么三角形面积相等
C. 如果三角形等底等高,那么面积相等
D. 如果两个三角形有一边和这边上的高相等,那么这两个三角形的面积相等
3、有一个三角形的三个内角都不相等,其中最小的角为47°,这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4、利用尺规作图,作不出唯一三角形是(?????? )
A.已知三边???????B.已知两边及其中一边的对角 C.已知两角及夹边????D.已知两边及夹角
5、如图,在△ABC中,点D在边BC上,点E、G分别是BF、AC的中点,若BC=3DC,△ABC的面积为12,则的值是( ).
A. B.1 C.2 D.3
6、下列命题中是真命题的是( )
A.只有无限循环小数才是有理数 B.只有开方开不尽的数才是无理数
C.只有正数才有平方根 D.只有实数才能与数轴上的点是一一对应的关系
7、如图,直线、,被直线所截,且∥,过上的点A作AB⊥于点B,其中,则下列一定正确的是( )
A. B. C. D.
8、在,∠A=43°,∠B=65°,∠ ,∠,且,那么这两个三角形( )
A.不一定全等 B.一定不全等 C.一定全等 D.以上都不对
9、如图,已知△ABC≌△DEF,CD平分∠BAC,若∠A=28°,∠CGF=85°则∠E的度数是( )
A.38° B.36° C.34° D.32°
10、如图,AE=AD,∠1=∠2,∠E=∠D,结论①BF=CG;②OF=OG;③EF=DG;④AG=GC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题 每题3分 共24分)
11、如图,BC⊥DE,垂足为G,AB=AD,AC=AE,BC=DE,问∠BAE+∠DAC= .
12、如图,在△ABC中,AC=BC,∠ACB=90°,点D是BC上的一点,过点B作BE∥AC,使BE=CD,
连接CE与AD相交于点G,则AD与CE的数量关系是 ,位置关系是 .
13、将一个三角形剪去一个角后,得到,∠1+∠2=220°,则∠A = (度).
14、如图,已知点B、D、E、C在BC上,∠1=∠2,BE=CD,再添加一个条件也不能判定△ABD≌△ACE是 .
15、如图,将一副三角板如图放置,两个直角顶点重合于点C,点B在等腰三角板的斜边DE上,如果∠ACD=10°,则∠ABD的度数是 .
16、在三角形中,到三边距离相等的点是 .
17、如图,四边形ABCD中,AC=AD,AC=6,∠BAD=∠BCD=90°,则四边形ABCD的面积为 .
18、如图,在△ABC中AB的垂直平分线BC的延长线于点E,AC的垂直平分线CB的延长线于
点D,已知∠BAC=50°,则∠DAE等于 .
三、解答题(共8题 共66分)
19、(满分7分)如图,已知线段a,b,∠α.画△ABC,使其中有一个内角等于∠α,且∠α的对边等于a,另外一边等于b.
20、(满分7分)如图,在△ABC中,AB>AC,AD是中线,
将三角形的周长分为15cm和12cm两部分,AB+AC=21,
求AB、AC的长.
21、(满分8分)如图∠1=∠2=∠3,AB=AD,AE=5,求AC的长度.
22、(满分8分)如图已知AD是MAN的平分线,点P在AD上,点C在AM上,点B在AN上,AC>AB,求证PC-PB<AC-AB.
23、(满分8分)已知四边形ABCD内角和为360°, BE平分∠ABC,DF平分∠ADC,BE∥FD,若∠C=90°,求证:∠A为直角.完成下面推理过程,并写出依据.
证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC( ),
∴∠ADC=2∠1( ).
∵BE平分∠ABC( ),
∴∠ABC=2∠3( ).
又∵BE∥FD( ),
∴∠2=∠3( ).
∴∠ABC=2∠2( ).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°( ).
又∵∠A+∠ABC+∠C+∠CDA=360°( ),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°.
24.(满分8分)如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,
使CF=BE(不再添加其它线段,
不再标注或使用其他字母),并给出证明.
25、(满分8分)如图,AF垂直平分BC,AD=CE,DB=AE,
求证:∠D=∠E.
26、(满分12分)如图,在△ABC中,高AD、BE相交于点H,连接CH并延长到G,使CG=AB,CG与AB相交于F,连接AG,若HD=CD,
求证:AH = AG.
参考答案
一、选择题(共10小题 每3分 共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
B
D
D
C
A
C
二、填空题(共8小题 每题3分 共24分)
11.90° 12.AD=CE ,AD⊥CE 13.40° 14.AB=AC 15.5° 16.三角形三条角平分线的交点
17.18 18.80°
三、解答题(共8题 共66分)
19.作法:1. ∠MAN=∠α,
2.在BM上截取BA= b,
3.以点A为圆心,a为半径画弧,交BN于点、,
、均为符合条件的所求三角形.
20.题解答:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长=AB+BD+AD,
??△ACD的周长=AC+CD+AD =AC+BD+AD,
∴△ABD的周长-△ACD的周长=AB-AC=3.
又∵AB+AC=21,
解方程组,得,AB=12,AC=9
答:AB和AC的长分别为12cm和9cm.
21.解:∵∠1=∠3(已知),
∠4=∠5(对顶角相等),
∴∠D=∠B(三角形内角和定理).
∵∠1=∠2(已知),
∴∠1+∠BAE=∠2+∠BAE(等量加等量和相等),
∴即∠DAE=∠BAC.
在△DAE和△BAC中,
∴△DAE≌△BAC(ASA).
∴AC=AE=(全等三角形对应边相等).
22.证明:在AM上截取AE=AB,连接EP,
在△AEP和△ABP中,
∴△AEP≌△ABP(SAS).
∴PE=PB(全等三角形对应边相等).
在△EPC中,
∵PC-PE<EC(三角形三边关系定理)
∴PC-PB<AC-AE(等量代换).
即PC-PB<AC-AB(等量代换).
23证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC(已知 ),
∴∠ADC=2∠1(角平分线定义).
∵BE平分∠ABC(已知 ),
∴∠ABC=2∠3(角平分线定义).
又∵BE∥FD(已知 ),
∴∠2=∠3(两直线平行,同位角相等).
∴∠ABC=2∠2(等量代换).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°(等量代换).
又∵∠A+∠ABC+∠C+∠CDA=360°(已知),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°(等式的性质).
24.解:(1)添加的条件是: BD=CD ;
(2)证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行内错角相等),
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA)
CF=BE(全等三角形对应边相等)
25.证明:连接AB、AC,
∵ AF垂直平分BC(已知),
∴ AB=AC(线段垂直平分线的性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(SSS)
∴∠D=∠E(全等三角形对应角相等).
26.证明:∵AD、BE是△ABC的高(已知),
∴∠BEC=∠ADC=∠ADB= 90°(垂直定义).
∴∠2+∠BCA=90°,∠4+∠BCA =90°(直角三角形两锐角互余).
∴∠2 =∠4(等式的性质).
△BHD和△ACD中,
∴△BHD≌△ACD(AAS).
∴BH=CA(全等三角形对应边相等).
∵H是高AD、BE的交点(已知),
∴CF⊥AB(三角形三条高相交于一点),
∴∠BEA=∠CFA=90°(垂直定义).
∴∠1+∠BAC=90°,∠3+∠BAC =90°(直角三角形两锐角互余).
∴∠1 =∠3(等式的性质).
△ABH和△GCA中,
∴△ABH≌△GCA(SAS).
第1章三角形的初步知识检测题2
(时间:100分钟 满分:120分)
题号
1
2
3
4
5
6
7
8
9
10
答案
一、选择题(共10小题 每3分 共30分)
1、若三角形的三边分别为5cm,8cm,()cm,则a的取值范围是( ).
A.3
A.如果等底等高,那么面积相等
B. 如果等底等高,那么三角形面积相等
C. 如果三角形等底等高,那么面积相等
D. 如果两个三角形有一边和这边上的高相等,那么这两个三角形的面积相等
3、有一个三角形的三个内角都不相等,其中最小的角为47°,这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4、利用尺规作图,作不出唯一三角形是(?????? )
A.已知三边???????B.已知两边及其中一边的对角 C.已知两角及夹边????D.已知两边及夹角
5、如图,在△ABC中,点D在边BC上,点E、G分别是BF、AC的中点,若BC=3DC,△ABC的面积为12,则的值是( ).
A. B.1 C.2 D.3
6、下列命题中是真命题的是( )
A.只有无限循环小数才是有理数 B.只有开方开不尽的数才是无理数
C.只有正数才有平方根 D.只有实数才能与数轴上的点是一一对应的关系
7、如图,直线、,被直线所截,且∥,过上的点A作AB⊥于点B,其中,则下列一定正确的是( )
A. B. C. D.
8、在,∠A=43°,∠B=65°,∠ ,∠,且,那么这两个三角形( )
A.不一定全等 B.一定不全等 C.一定全等 D.以上都不对
9、如图,已知△ABC≌△DEF,CD平分∠BAC,若∠A=28°,∠CGF=85°则∠E的度数是( )
A.38° B.36° C.34° D.32°
10、如图,AE=AD,∠1=∠2,∠E=∠D,结论①BF=CG;②OF=OG;③EF=DG;④AG=GC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题 每题3分 共24分)
11、如图,BC⊥DE,垂足为G,AB=AD,AC=AE,BC=DE,问∠BAE+∠DAC= .
12、如图,在△ABC中,AC=BC,∠ACB=90°,点D是BC上的一点,过点B作BE∥AC,使BE=CD,
连接CE与AD相交于点G,则AD与CE的数量关系是 ,位置关系是 .
13、将一个三角形剪去一个角后,得到,∠1+∠2=220°,则∠A = (度).
14、如图,已知点B、D、E、C在BC上,∠1=∠2,BE=CD,再添加一个条件也不能判定△ABD≌△ACE是 .
15、如图,将一副三角板如图放置,两个直角顶点重合于点C,点B在等腰三角板的斜边DE上,如果∠ACD=10°,则∠ABD的度数是 .
16、在三角形中,到三边距离相等的点是 .
17、如图,四边形ABCD中,AC=AD,AC=6,∠BAD=∠BCD=90°,则四边形ABCD的面积为 .
18、如图,在△ABC中AB的垂直平分线BC的延长线于点E,AC的垂直平分线CB的延长线于
点D,已知∠BAC=50°,则∠DAE等于 .
三、解答题(共8题 共66分)
19、(满分7分)如图,已知线段a,b,∠α.画△ABC,使其中有一个内角等于∠α,且∠α的对边等于a,另外一边等于b.
20、(满分7分)如图,在△ABC中,AB>AC,AD是中线,
将三角形的周长分为15cm和12cm两部分,AB+AC=21,
求AB、AC的长.
21、(满分8分)如图∠1=∠2=∠3,AB=AD,AE=5,求AC的长度.
22、(满分8分)如图已知AD是MAN的平分线,点P在AD上,点C在AM上,点B在AN上,AC>AB,求证PC-PB<AC-AB.
23、(满分8分)已知四边形ABCD内角和为360°, BE平分∠ABC,DF平分∠ADC,BE∥FD,若∠C=90°,求证:∠A为直角.完成下面推理过程,并写出依据.
证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC( ),
∴∠ADC=2∠1( ).
∵BE平分∠ABC( ),
∴∠ABC=2∠3( ).
又∵BE∥FD( ),
∴∠2=∠3( ).
∴∠ABC=2∠2( ).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°( ).
又∵∠A+∠ABC+∠C+∠CDA=360°( ),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°.
24.(满分8分)如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,
使CF=BE(不再添加其它线段,
不再标注或使用其他字母),并给出证明.
25、(满分8分)如图,AF垂直平分BC,AD=CE,DB=AE,
求证:∠D=∠E.
26、(满分12分)如图,在△ABC中,高AD、BE相交于点H,连接CH并延长到G,使CG=AB,CG与AB相交于F,连接AG,若HD=CD,
求证:AH = AG.
参考答案
一、选择题(共10小题 每3分 共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
B
D
D
C
A
C
二、填空题(共8小题 每题3分 共24分)
11.90° 12.AD=CE ,AD⊥CE 13.40° 14.AB=AC 15.5° 16.三角形三条角平分线的交点
17.18 18.80°
三、解答题(共8题 共66分)
19.作法:1. ∠MAN=∠α,
2.在BM上截取BA= b,
3.以点A为圆心,a为半径画弧,交BN于点、,
、均为符合条件的所求三角形.
20.题解答:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长=AB+BD+AD,
??△ACD的周长=AC+CD+AD =AC+BD+AD,
∴△ABD的周长-△ACD的周长=AB-AC=3.
又∵AB+AC=21,
解方程组,得,AB=12,AC=9
答:AB和AC的长分别为12cm和9cm.
21.解:∵∠1=∠3(已知),
∠4=∠5(对顶角相等),
∴∠D=∠B(三角形内角和定理).
∵∠1=∠2(已知),
∴∠1+∠BAE=∠2+∠BAE(等量加等量和相等),
∴即∠DAE=∠BAC.
在△DAE和△BAC中,
∴△DAE≌△BAC(ASA).
∴AC=AE=(全等三角形对应边相等).
22.证明:在AM上截取AE=AB,连接EP,
在△AEP和△ABP中,
∴△AEP≌△ABP(SAS).
∴PE=PB(全等三角形对应边相等).
在△EPC中,
∵PC-PE<EC(三角形三边关系定理)
∴PC-PB<AC-AE(等量代换).
即PC-PB<AC-AB(等量代换).
23证明:∵∠C=90°( ),
∴∠1+∠2=90°( ).
∵DF平分∠ADC(已知 ),
∴∠ADC=2∠1(角平分线定义).
∵BE平分∠ABC(已知 ),
∴∠ABC=2∠3(角平分线定义).
又∵BE∥FD(已知 ),
∴∠2=∠3(两直线平行,同位角相等).
∴∠ABC=2∠2(等量代换).
∴∠ABC+∠ADC=2∠1+2∠2=2(∠1+∠2)=2×90°=180°(等量代换).
又∵∠A+∠ABC+∠C+∠CDA=360°(已知),
∴∠A=360°-∠C -(∠ABC+∠CDA)
=360°-90°-180°=90°(等式的性质).
24.解:(1)添加的条件是: BD=CD ;
(2)证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行内错角相等),
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA)
CF=BE(全等三角形对应边相等)
25.证明:连接AB、AC,
∵ AF垂直平分BC(已知),
∴ AB=AC(线段垂直平分线的性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(SSS)
∴∠D=∠E(全等三角形对应角相等).
26.证明:∵AD、BE是△ABC的高(已知),
∴∠BEC=∠ADC=∠ADB= 90°(垂直定义).
∴∠2+∠BCA=90°,∠4+∠BCA =90°(直角三角形两锐角互余).
∴∠2 =∠4(等式的性质).
△BHD和△ACD中,
∴△BHD≌△ACD(AAS).
∴BH=CA(全等三角形对应边相等).
∵H是高AD、BE的交点(已知),
∴CF⊥AB(三角形三条高相交于一点),
∴∠BEA=∠CFA=90°(垂直定义).
∴∠1+∠BAC=90°,∠3+∠BAC =90°(直角三角形两锐角互余).
∴∠1 =∠3(等式的性质).
△ABH和△GCA中,
∴△ABH≌△GCA(SAS).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
