3.2 图形的旋转同步课时作业
图片预览




文档简介
3.2 图形的旋转同步课时作业
姓名:___________班级:___________考号:___________
一、选择题
1.如图,已知点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,则下列说法正确的是( )
A. △ODE绕点O顺时针旋转60°得到△OBC B. △ODE绕点O逆时针旋转120°得到△OAB
C. △ODE绕点F顺时针旋转60°得到△OAB D. △ODE绕点C逆时针旋转90°得△OAB
2.有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图 ①,第2次旋转后得到图6②,…,则第10次旋转后得到的图形与图①~④中相同的是( )
A. 图① B. 图② C. 图③ D. 图④
3.如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
A. (1,1) B. (0,1) C. (-1,1) D. (2,0)
4.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
A. (5,2) B. (2,5) C. (2,﹣5) D. (5,﹣2)
5.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A. 12 B. 6 C. 6 D.
6.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于(?? )
A. B. C. D.
7.在图中,将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
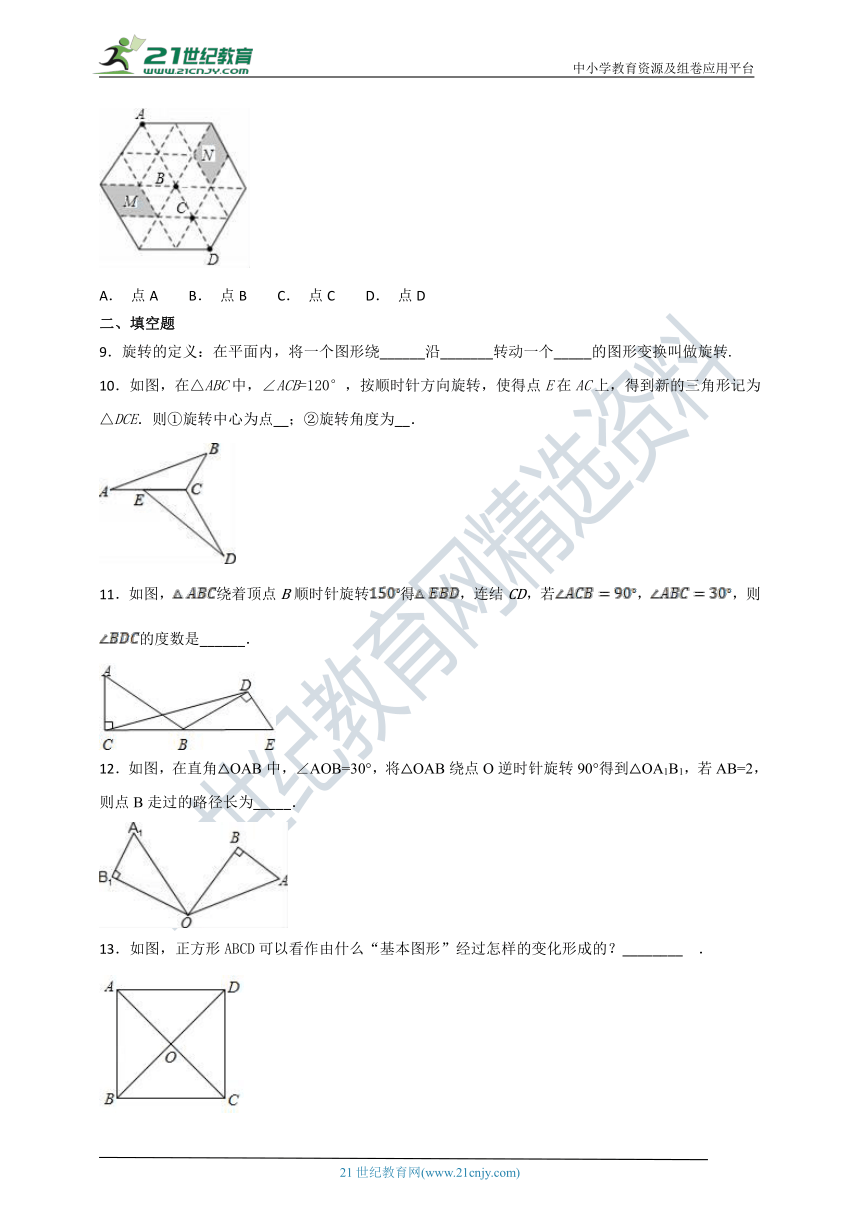
8.如图,在正三角形网格中,菱形M经过旋转变换能得到菱形N,下列四个点中能作为旋转中心的是( )
A. 点A B. 点B C. 点C D. 点D
二、填空题
9.旋转的定义:在平面内,将一个图形绕______沿_______转动一个_____的图形变换叫做旋转.
10.如图,在△ABC中,∠ACB=120°,按顺时针方向旋转,使得点E在AC上,得到新的三角形记为△DCE.则①旋转中心为点__;②旋转角度为__.
11.如图,绕着顶点B顺时针旋转得,连结CD,若,,则的度数是______.
12.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转90°得到△OA1B1,若AB=2,则点B走过的路径长为_____.
13.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________?.
14.如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
15.如图,在矩形ABCD中,AB=1,BC=7,将矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′,点E、F分别是BD、B′D′的中点,则EF的长度为________cm.
三、解答题
16.如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.
(1)问△ABC与△ADE的关系如何?
(2)求∠BAD的度数.
17.钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心.;
(2)经过45分钟,分针旋转了多少度?
18.如图,将Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,若AC⊥A′B′,求∠ABC的度数.
19.如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.
20.如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
21.如图,在中,,,D是AB边上一点点D与A,B不重合,连结CD,将线段CD绕点C按逆时针方向旋转得到线段CE,连结DE交BC于点F,连接BE.
求证:≌;
当时,求的度数.
参考答案
1.C
【解析】
【分析】
由于点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,根据旋转的性质得到△ODE绕点O顺时针旋转120°得到△OBC,于是可对A、B进行判断;△ODE绕点F顺时针旋转60°时,点O旋转到点A得,点E旋转到点O,点D旋转到点B,则可对C进行判断;利用ODE绕点C顺时针旋转60°得到△OBC可对D进行判断.
【详解】
A、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点O顺时针旋转120°得到△OBC,所以A选项错误;
B、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点O顺时针旋转120°得到△OBC,所以B选项错误;
C、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点F顺时针旋转60°时,点O旋转到点A得,点E旋转到点O,点D旋转到点B,所以C选项正确;
D、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点C顺时针旋转60°得到△OBC,所以D选项错误.
故选:C
【点睛】
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正六边形和等边三角形的性质.
2.B
【解析】
试题分析:依题意,旋转10次共旋转了10×45°=450°,
因为450°-360°=90°,
所以,第10次旋转后得到的图形与图②相同,
故选B.
点睛:根据图中给出的旋转规律,得知变化为周期性变化,结合周角的定义即可解答本题.
3.B
【解析】根据旋转的性质:对应点到旋转中心的距离相等,可知,只要连接两组对应点,作出对应点所连线段的两条垂直平分线,其交点即为旋转中心.
解:如图,
连接AD、BE,作线段AD、BE的垂直平分线,
两线的交点即为旋转中心O′.其坐标是(0,1).
故选B..
4.A
【解析】试题解析:作AD⊥x轴于点D,作A′D′⊥x轴于点D′,
则OD=A′D′,AD=OD′,OA=OA′,
∴△OAD≌△A′OD′(SSS),
∵A(-2,5),
∴OD=2,AD=5,
∴点A′的坐标为(5,2),
故选A.
5.D
【解析】
【分析】
连接B'B,利用旋转的性质和直角三角形的性质解答即可.
【详解】
连接B'B,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴AC=A'C,AB=A'B,∠A=∠CA'B'=60°,
∴△AA'C是等边三角形,
∴∠AA'C=60°,
∴∠B'A'B=180°-60°-60°=60°,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴∠ACA'=∠BAB'=60°,BC=B'C,∠CB'A'=∠CBA=90°-60°=30°,
∴△BCB'是等边三角形,
∴∠CB'B=60°,
∵∠CB'A'=30°,
∴∠A'B'B=30°,
∴∠B'BA'=180°-60°-30°=90°,
∵∠ACB=90°,∠A=60°,AC=6,
∴AB=12,
∴A'B=AB-AA'=AB-AC=6,
∴B'B=6,
故选D.
【点睛】
此题考查旋转问题,关键是利用旋转的性质和直角三角形的性质解答.
6.B
【解析】分析:设CD、B′C′相交于点M,连结AM,根据旋转角的定义易得:∠BAB′=30°,根据HL易得△AB′M≌△ADM,所以公共部分面积等于△ADM面积的2倍;
设DM=x,在△AMD中利用勾股定理求得DM,进而解答即可.
详解:设CD、B′C′相交于点M,连结AM,设DM=x,根据旋转的性质以及正方形的性质可得AB′=AD,AM=AM,∠BAB′=30°,∠B′=∠D=90°.
∵AB′=AD,AM=AM,
∴△AB′M≌△ADM.
∵∠BAB′=30°,
∴∠MAD=30°, AM=2x.
∵x2+1=4x2,
∴x=,
∴SADM′=,
∴重叠部分的面积SADMB′==.
故选B.
点睛:本题考查了正方形的性质,旋转的性质,含30°三角形的性质,勾股定理,全等三角形的判定与性质,证明△AB′M≌△ADM是解答本题的关键;
7.B
【解析】分析:根据旋转的性质,找出图中三角形的关键处(旋转中心)按顺时针方向旋转90°后的形状即可选择答案.
详解:根据旋转的性质可知,绕O点顺时针旋转90°得到的图形是 .
故选B.
点睛:本题考查了旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
8.D
【解析】直接利用旋转的性质结合等边三角形的性质进而分析得出答案,
如图所示:菱形M绕点D经过顺时针旋转60°变换能得到菱形N,
故选D.
9. 一个点 一个方向 角度
【解析】在平面内,将一个图形绕着一个定点沿一个方向转动一个角度的图形变换称为旋转,
故答案为:一个点,一个方向,角度.
10. C 240°
【解析】由图可知旋转中心是点C,旋转角度为360°-120°=240°.
点睛:本题主要考查旋转的性质,能正确地识图是解决问题的关键.
11.15°
【解析】
【分析】
根据旋转的性质得到BD=CB,由等腰三角形的性质得到∠DCB=∠BDC,根据三角形的外角的性质即可得到结论.
【详解】
∵△ABC绕着顶点B顺时针旋转150°得△EBD, ∴BD=CB, ∴∠DCB=∠BDC 又∵∠DBE=∠ABC=30°,∠DBE=∠DCB+∠BDC 故∠BDC=∠DBE=15°, 故答案是:15°.
【点睛】
考查了旋转的性质,等腰三角形的性质,熟练掌握旋转的性质(图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等)是解题的关键.
12.π
【解析】分析:三角形旋转以后,B点的路径是一个圆弧,再用弧长公式,计算B走过的路径,此时圆弧的半径是OB长,利用特殊三角形求OB.
详解:
解:∵在直角△OAB中,∠AOB=30°,AB=2,
∴OB=AB=2,
∵将△OAB绕点O逆时针旋转90°得到△OA1B1,
∴∠BOB1=90°,
∴点B走过的路径长为π
故答案为π
点睛:(1)30°角的直角三角形,三边比为1:2:,需要熟练掌握,
(2)弧长公式=.
13.把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
【解析】观察图形可知把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.
故答案为:把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.
14.4
【解析】分析:根据旋转后AC的中点恰好与D点重合,利用旋转的性质得到直角三角形ACD中,∠ACD=30°,再由旋转后矩形与已知矩形全等及矩形的性质得到∠DAE为30°,进而得到∠EAC=∠ECA,利用等角对等边得到AE=CE,设AE=CE=x,表示出AD与DE,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出EC的长,即可求出三角形AEC面积.
详解:∵旋转后AC的中点恰好与D点重合,即AD=AC′=AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,∴∠DAE=30°,
∴∠EAC=∠ACD=30°,∴AE=CE.
在Rt△ADE中,设AE=EC=x,
则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=×6=2,
根据勾股定理得:x2=(6﹣x)2+(2)2,
解得:x=4,∴EC=4,
则S△AEC=EC?AD=4.
故答案为:4.
点睛:本题考查了旋转的性质,含30度直角三角形的性质,勾股定理以及等腰三角形的性质的运用,熟练掌握性质及定理是解答本题的关键.
15.5
【解析】【分析】如图,连接AC、A′C,AA′,由矩形的性质和勾股定理求出AC长,由矩形的性质得出E是AC的中点,F是A′C的中点,证出EF是△ACA′的中位线,由三角形中位线定理得出EF=AA′,由等腰直角三角形的性质得出AA′=AC,即可得出结果.
【详解】如图,连接AC、A′C,AA′,
∵矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′,
∴∠ACA′=90°,∠ABC=90°,
∴AC=,AC=BD=A′C=B′D′,
AC与BD互相平分,A′C与B′D′互相平分,
∵点E、F分别是BD、B′D′的中点,
∴E是AC的中点,F是A′C的中点,
∵∠ACA′=90°,∴△ACA′是等腰直角三角形,
∴AA′=AC==10,
∴EF=AA′=5,
故答案为:5.
【点睛】本题考查了矩形的性质、旋转的性质、勾股定理、等腰直角三角形的判定与性质,三角形的中位线定理,熟练掌握矩形的性质,由三角形的中位线定理求出EF长是解决问题的关键.
16.(1)△ABC≌△ADE;(2)30°
【解析】由旋转的性质和三角形的性质即可解答.
解:(1)∵△ABC绕其顶点A顺时针旋转30°后得△ADE,∴△ABC≌△ADE.
(2)旋转角相等,即∠BAD=∠EAC=30°.
17.(1)它的旋转中心是表盘中心;(2)45分钟旋转的角度是270°.
【解析】【分析】(1)由旋转定义可得;(2)由于时针旋转一周为12小时,则时针每小时旋转的度数=360°÷12=30°,分针旋转一周为60分,则分针每分旋转的度数=360°÷60=6°,从而使问题得以解决.
【详解】
解:(1)它的旋转中心是表盘中心.
(2)分针一周要60分钟,正好旋转了360°,而45分钟旋转的角度是: ×360°=270°.
【点睛】本题考核知识点:旋转的定义,钟面角.解答本题的关键是了解时针每小时旋转的度数、分针每分钟旋转的度数.
18.38°.
【解析】分析:
如下图所示,设AC与A′B′的交点为O,则由已知条件易得∠A′OC=90°,∠ACA′=38°,由此可得∠A′=52°,由旋转的性质可得∠A=52°,结合∠ACB=90°即可得到∠ABC=38°.
详解:
∵Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,
∴∠ACA′=38°,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′OC=90°,
∴∠A′=90°-38°=52°,
∴∠A=52°,
又∵在Rt△ABC中,∠ACB=90°,
∴∠ABC=180°-90°-52°=38°.
点睛:“由旋转的性质得到∠ACA′=38°,结合AC⊥A′B′得到∠A′=52°=∠A”是解答本题的关键.
19.86°.
【解析】试题分析:由菱形的性质有BC=CD,∠BCD=∠A=110°,根据旋转的性质知CE=CF,∠ECF=∠BCD=110°,于是得到∠BCE=∠DCF=110°﹣∠DCE,根据三角形的判定证得△BCE≌△DCF,根据三角形的性质即可得到结论.
试题解析:解:∵菱形ABCD,∴BC=CD,∠BCD=∠A=110°,由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,∴∠BCE=∠DCF=110°﹣∠DCE,在△BCE和△DCF中,∵BC=CD,∠BCE=∠DCF,CE=CF,∴△BCE≌△DCF,∴∠F=∠E=86°.
点睛:本题主要考查了菱形的性质,旋转的性质,三角形的性质和判定,由旋转的性质得到CE=CF,∠ECF=∠BCD是解题的关键.
20.(1)A,90°;(2)3;(3)BE⊥DF,理由见解析.
【解析】(1)(2)利用旋转的定义和性质即可得出答案;(3)利用旋转证出△ABE≌△ADF,再通过全等三角形的性质、三角形内角和即可证出.
解:(1)旋转中心为点A,旋转角度为90°;
(2)DE=AD-AE=7-4=3;
(3)BE⊥DF.理由如下:
延长BE与DF交于点M
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴∠ABE=∠ADF,
∵∠ADF+∠F=180°-90°=90°,
∴∠ABE+∠F=90°,
即∠BMF=90°,∴BE⊥DF.
21.证明见解析;.
【解析】【分析】由题意可知:,,由于,从而可得,根据SAS即可证明≌;
由≌可知:,,从而可求出的度数.
【详解】由题意可知:,,
,
,
,
,
在与中,
,
≌;
,,
,
由可知:,
,
,
.
【点睛】本题考查了旋转的性质、全等三角形的判定与性质,解题的关键是熟练运用旋转的性质以及全等三角形的判定与性质.
姓名:___________班级:___________考号:___________
一、选择题
1.如图,已知点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,则下列说法正确的是( )
A. △ODE绕点O顺时针旋转60°得到△OBC B. △ODE绕点O逆时针旋转120°得到△OAB
C. △ODE绕点F顺时针旋转60°得到△OAB D. △ODE绕点C逆时针旋转90°得△OAB
2.有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图 ①,第2次旋转后得到图6②,…,则第10次旋转后得到的图形与图①~④中相同的是( )
A. 图① B. 图② C. 图③ D. 图④
3.如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
A. (1,1) B. (0,1) C. (-1,1) D. (2,0)
4.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
A. (5,2) B. (2,5) C. (2,﹣5) D. (5,﹣2)
5.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A. 12 B. 6 C. 6 D.
6.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于(?? )
A. B. C. D.
7.在图中,将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
8.如图,在正三角形网格中,菱形M经过旋转变换能得到菱形N,下列四个点中能作为旋转中心的是( )
A. 点A B. 点B C. 点C D. 点D
二、填空题
9.旋转的定义:在平面内,将一个图形绕______沿_______转动一个_____的图形变换叫做旋转.
10.如图,在△ABC中,∠ACB=120°,按顺时针方向旋转,使得点E在AC上,得到新的三角形记为△DCE.则①旋转中心为点__;②旋转角度为__.
11.如图,绕着顶点B顺时针旋转得,连结CD,若,,则的度数是______.
12.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转90°得到△OA1B1,若AB=2,则点B走过的路径长为_____.
13.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________?.
14.如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
15.如图,在矩形ABCD中,AB=1,BC=7,将矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′,点E、F分别是BD、B′D′的中点,则EF的长度为________cm.
三、解答题
16.如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.
(1)问△ABC与△ADE的关系如何?
(2)求∠BAD的度数.
17.钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心.;
(2)经过45分钟,分针旋转了多少度?
18.如图,将Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,若AC⊥A′B′,求∠ABC的度数.
19.如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.
20.如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
21.如图,在中,,,D是AB边上一点点D与A,B不重合,连结CD,将线段CD绕点C按逆时针方向旋转得到线段CE,连结DE交BC于点F,连接BE.
求证:≌;
当时,求的度数.
参考答案
1.C
【解析】
【分析】
由于点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,根据旋转的性质得到△ODE绕点O顺时针旋转120°得到△OBC,于是可对A、B进行判断;△ODE绕点F顺时针旋转60°时,点O旋转到点A得,点E旋转到点O,点D旋转到点B,则可对C进行判断;利用ODE绕点C顺时针旋转60°得到△OBC可对D进行判断.
【详解】
A、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点O顺时针旋转120°得到△OBC,所以A选项错误;
B、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点O顺时针旋转120°得到△OBC,所以B选项错误;
C、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点F顺时针旋转60°时,点O旋转到点A得,点E旋转到点O,点D旋转到点B,所以C选项正确;
D、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点C顺时针旋转60°得到△OBC,所以D选项错误.
故选:C
【点睛】
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正六边形和等边三角形的性质.
2.B
【解析】
试题分析:依题意,旋转10次共旋转了10×45°=450°,
因为450°-360°=90°,
所以,第10次旋转后得到的图形与图②相同,
故选B.
点睛:根据图中给出的旋转规律,得知变化为周期性变化,结合周角的定义即可解答本题.
3.B
【解析】根据旋转的性质:对应点到旋转中心的距离相等,可知,只要连接两组对应点,作出对应点所连线段的两条垂直平分线,其交点即为旋转中心.
解:如图,
连接AD、BE,作线段AD、BE的垂直平分线,
两线的交点即为旋转中心O′.其坐标是(0,1).
故选B..
4.A
【解析】试题解析:作AD⊥x轴于点D,作A′D′⊥x轴于点D′,
则OD=A′D′,AD=OD′,OA=OA′,
∴△OAD≌△A′OD′(SSS),
∵A(-2,5),
∴OD=2,AD=5,
∴点A′的坐标为(5,2),
故选A.
5.D
【解析】
【分析】
连接B'B,利用旋转的性质和直角三角形的性质解答即可.
【详解】
连接B'B,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴AC=A'C,AB=A'B,∠A=∠CA'B'=60°,
∴△AA'C是等边三角形,
∴∠AA'C=60°,
∴∠B'A'B=180°-60°-60°=60°,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴∠ACA'=∠BAB'=60°,BC=B'C,∠CB'A'=∠CBA=90°-60°=30°,
∴△BCB'是等边三角形,
∴∠CB'B=60°,
∵∠CB'A'=30°,
∴∠A'B'B=30°,
∴∠B'BA'=180°-60°-30°=90°,
∵∠ACB=90°,∠A=60°,AC=6,
∴AB=12,
∴A'B=AB-AA'=AB-AC=6,
∴B'B=6,
故选D.
【点睛】
此题考查旋转问题,关键是利用旋转的性质和直角三角形的性质解答.
6.B
【解析】分析:设CD、B′C′相交于点M,连结AM,根据旋转角的定义易得:∠BAB′=30°,根据HL易得△AB′M≌△ADM,所以公共部分面积等于△ADM面积的2倍;
设DM=x,在△AMD中利用勾股定理求得DM,进而解答即可.
详解:设CD、B′C′相交于点M,连结AM,设DM=x,根据旋转的性质以及正方形的性质可得AB′=AD,AM=AM,∠BAB′=30°,∠B′=∠D=90°.
∵AB′=AD,AM=AM,
∴△AB′M≌△ADM.
∵∠BAB′=30°,
∴∠MAD=30°, AM=2x.
∵x2+1=4x2,
∴x=,
∴SADM′=,
∴重叠部分的面积SADMB′==.
故选B.
点睛:本题考查了正方形的性质,旋转的性质,含30°三角形的性质,勾股定理,全等三角形的判定与性质,证明△AB′M≌△ADM是解答本题的关键;
7.B
【解析】分析:根据旋转的性质,找出图中三角形的关键处(旋转中心)按顺时针方向旋转90°后的形状即可选择答案.
详解:根据旋转的性质可知,绕O点顺时针旋转90°得到的图形是 .
故选B.
点睛:本题考查了旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
8.D
【解析】直接利用旋转的性质结合等边三角形的性质进而分析得出答案,
如图所示:菱形M绕点D经过顺时针旋转60°变换能得到菱形N,
故选D.
9. 一个点 一个方向 角度
【解析】在平面内,将一个图形绕着一个定点沿一个方向转动一个角度的图形变换称为旋转,
故答案为:一个点,一个方向,角度.
10. C 240°
【解析】由图可知旋转中心是点C,旋转角度为360°-120°=240°.
点睛:本题主要考查旋转的性质,能正确地识图是解决问题的关键.
11.15°
【解析】
【分析】
根据旋转的性质得到BD=CB,由等腰三角形的性质得到∠DCB=∠BDC,根据三角形的外角的性质即可得到结论.
【详解】
∵△ABC绕着顶点B顺时针旋转150°得△EBD, ∴BD=CB, ∴∠DCB=∠BDC 又∵∠DBE=∠ABC=30°,∠DBE=∠DCB+∠BDC 故∠BDC=∠DBE=15°, 故答案是:15°.
【点睛】
考查了旋转的性质,等腰三角形的性质,熟练掌握旋转的性质(图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等)是解题的关键.
12.π
【解析】分析:三角形旋转以后,B点的路径是一个圆弧,再用弧长公式,计算B走过的路径,此时圆弧的半径是OB长,利用特殊三角形求OB.
详解:
解:∵在直角△OAB中,∠AOB=30°,AB=2,
∴OB=AB=2,
∵将△OAB绕点O逆时针旋转90°得到△OA1B1,
∴∠BOB1=90°,
∴点B走过的路径长为π
故答案为π
点睛:(1)30°角的直角三角形,三边比为1:2:,需要熟练掌握,
(2)弧长公式=.
13.把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
【解析】观察图形可知把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.
故答案为:把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.
14.4
【解析】分析:根据旋转后AC的中点恰好与D点重合,利用旋转的性质得到直角三角形ACD中,∠ACD=30°,再由旋转后矩形与已知矩形全等及矩形的性质得到∠DAE为30°,进而得到∠EAC=∠ECA,利用等角对等边得到AE=CE,设AE=CE=x,表示出AD与DE,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出EC的长,即可求出三角形AEC面积.
详解:∵旋转后AC的中点恰好与D点重合,即AD=AC′=AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,∴∠DAE=30°,
∴∠EAC=∠ACD=30°,∴AE=CE.
在Rt△ADE中,设AE=EC=x,
则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=×6=2,
根据勾股定理得:x2=(6﹣x)2+(2)2,
解得:x=4,∴EC=4,
则S△AEC=EC?AD=4.
故答案为:4.
点睛:本题考查了旋转的性质,含30度直角三角形的性质,勾股定理以及等腰三角形的性质的运用,熟练掌握性质及定理是解答本题的关键.
15.5
【解析】【分析】如图,连接AC、A′C,AA′,由矩形的性质和勾股定理求出AC长,由矩形的性质得出E是AC的中点,F是A′C的中点,证出EF是△ACA′的中位线,由三角形中位线定理得出EF=AA′,由等腰直角三角形的性质得出AA′=AC,即可得出结果.
【详解】如图,连接AC、A′C,AA′,
∵矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′,
∴∠ACA′=90°,∠ABC=90°,
∴AC=,AC=BD=A′C=B′D′,
AC与BD互相平分,A′C与B′D′互相平分,
∵点E、F分别是BD、B′D′的中点,
∴E是AC的中点,F是A′C的中点,
∵∠ACA′=90°,∴△ACA′是等腰直角三角形,
∴AA′=AC==10,
∴EF=AA′=5,
故答案为:5.
【点睛】本题考查了矩形的性质、旋转的性质、勾股定理、等腰直角三角形的判定与性质,三角形的中位线定理,熟练掌握矩形的性质,由三角形的中位线定理求出EF长是解决问题的关键.
16.(1)△ABC≌△ADE;(2)30°
【解析】由旋转的性质和三角形的性质即可解答.
解:(1)∵△ABC绕其顶点A顺时针旋转30°后得△ADE,∴△ABC≌△ADE.
(2)旋转角相等,即∠BAD=∠EAC=30°.
17.(1)它的旋转中心是表盘中心;(2)45分钟旋转的角度是270°.
【解析】【分析】(1)由旋转定义可得;(2)由于时针旋转一周为12小时,则时针每小时旋转的度数=360°÷12=30°,分针旋转一周为60分,则分针每分旋转的度数=360°÷60=6°,从而使问题得以解决.
【详解】
解:(1)它的旋转中心是表盘中心.
(2)分针一周要60分钟,正好旋转了360°,而45分钟旋转的角度是: ×360°=270°.
【点睛】本题考核知识点:旋转的定义,钟面角.解答本题的关键是了解时针每小时旋转的度数、分针每分钟旋转的度数.
18.38°.
【解析】分析:
如下图所示,设AC与A′B′的交点为O,则由已知条件易得∠A′OC=90°,∠ACA′=38°,由此可得∠A′=52°,由旋转的性质可得∠A=52°,结合∠ACB=90°即可得到∠ABC=38°.
详解:
∵Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,
∴∠ACA′=38°,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′OC=90°,
∴∠A′=90°-38°=52°,
∴∠A=52°,
又∵在Rt△ABC中,∠ACB=90°,
∴∠ABC=180°-90°-52°=38°.
点睛:“由旋转的性质得到∠ACA′=38°,结合AC⊥A′B′得到∠A′=52°=∠A”是解答本题的关键.
19.86°.
【解析】试题分析:由菱形的性质有BC=CD,∠BCD=∠A=110°,根据旋转的性质知CE=CF,∠ECF=∠BCD=110°,于是得到∠BCE=∠DCF=110°﹣∠DCE,根据三角形的判定证得△BCE≌△DCF,根据三角形的性质即可得到结论.
试题解析:解:∵菱形ABCD,∴BC=CD,∠BCD=∠A=110°,由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,∴∠BCE=∠DCF=110°﹣∠DCE,在△BCE和△DCF中,∵BC=CD,∠BCE=∠DCF,CE=CF,∴△BCE≌△DCF,∴∠F=∠E=86°.
点睛:本题主要考查了菱形的性质,旋转的性质,三角形的性质和判定,由旋转的性质得到CE=CF,∠ECF=∠BCD是解题的关键.
20.(1)A,90°;(2)3;(3)BE⊥DF,理由见解析.
【解析】(1)(2)利用旋转的定义和性质即可得出答案;(3)利用旋转证出△ABE≌△ADF,再通过全等三角形的性质、三角形内角和即可证出.
解:(1)旋转中心为点A,旋转角度为90°;
(2)DE=AD-AE=7-4=3;
(3)BE⊥DF.理由如下:
延长BE与DF交于点M
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴∠ABE=∠ADF,
∵∠ADF+∠F=180°-90°=90°,
∴∠ABE+∠F=90°,
即∠BMF=90°,∴BE⊥DF.
21.证明见解析;.
【解析】【分析】由题意可知:,,由于,从而可得,根据SAS即可证明≌;
由≌可知:,,从而可求出的度数.
【详解】由题意可知:,,
,
,
,
,
在与中,
,
≌;
,,
,
由可知:,
,
,
.
【点睛】本题考查了旋转的性质、全等三角形的判定与性质,解题的关键是熟练运用旋转的性质以及全等三角形的判定与性质.
同课章节目录
