3.3 垂径定理同步课时作业(1)
图片预览



文档简介
3.3 垂径定理同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
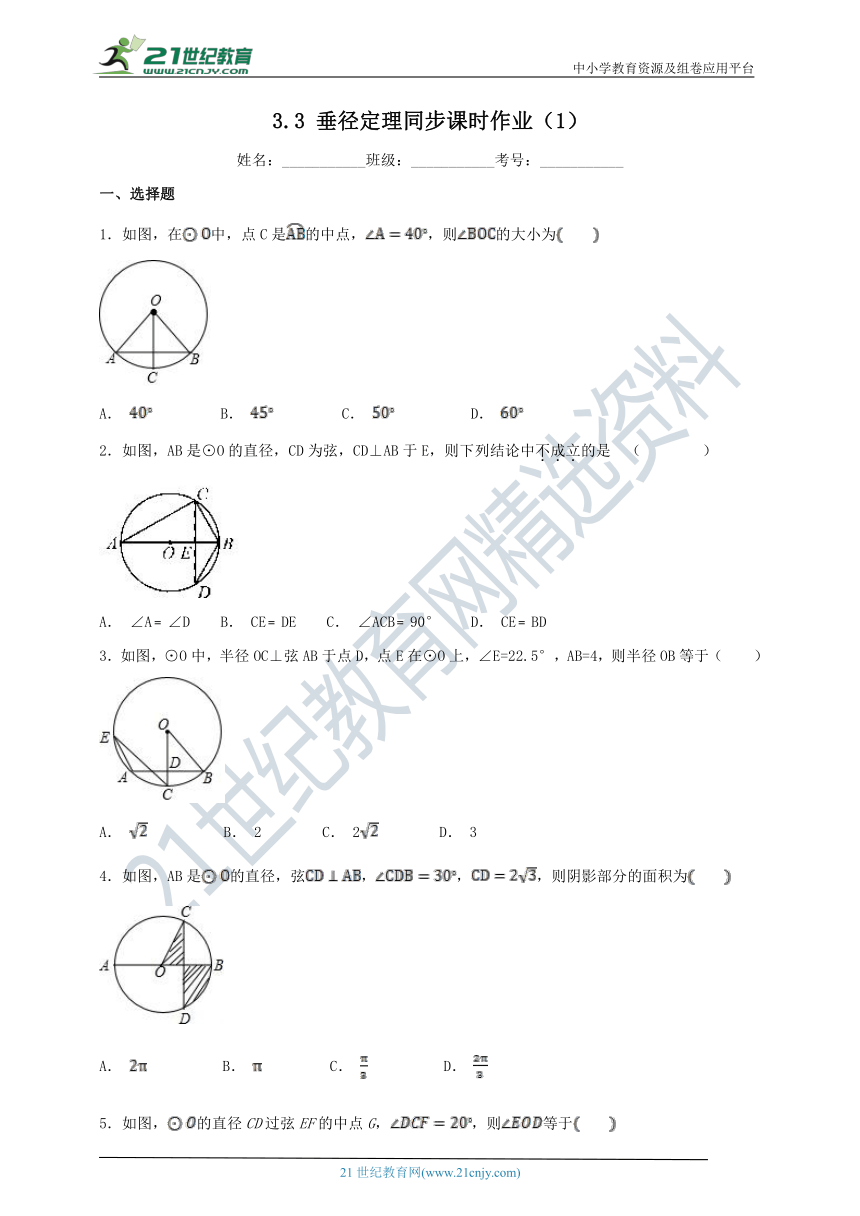
1.如图,在中,点C是的中点,,则的大小为
A. B. C. D.
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是 ( )
A. ∠A﹦∠D B. CE﹦DE C. ∠ACB﹦90° D. CE﹦BD
3.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A. B. 2 C. 2 D. 3
4.如图,AB是的直径,弦,,,则阴影部分的面积为
A. B. C. D.
5.如图,的直径CD过弦EF的中点G,,则等于
A. B. C. D.
6.如图,AB是⊙O的直径,AB⊥CD于点E,若CD=8,AE=2,则OE长为( )
A. B. C. D.
7.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为( )
A. B. C. D.
8.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A. 13寸 B. 20寸 C. 26寸 D. 28寸
二、填空题
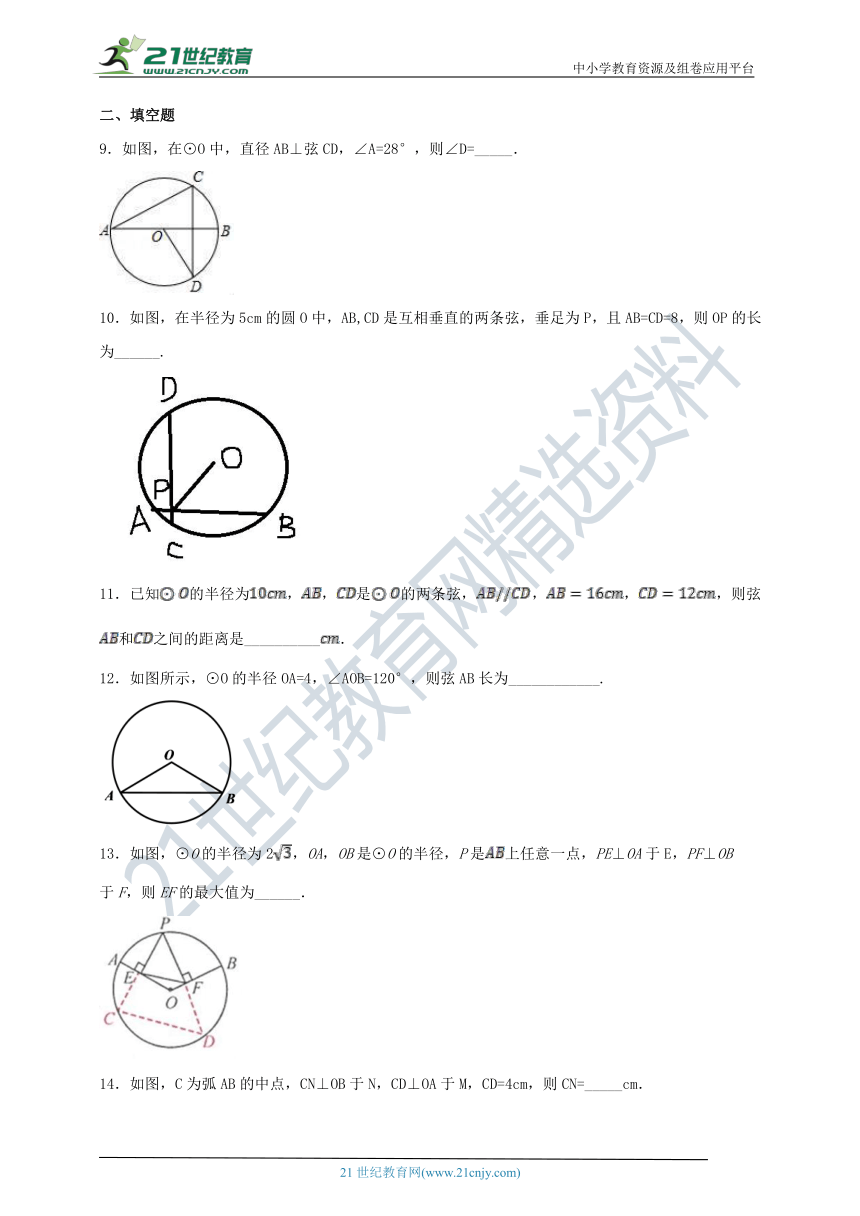
9.如图,在⊙O中,直径AB⊥弦CD,∠A=28°,则∠D=_____.
10.如图,在半径为5cm的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为______.
11.已知的半径为,,是的两条弦,,,,则弦和之间的距离是__________.
12.如图所示,⊙O的半径OA=4,∠AOB=120°,则弦AB长为____________.?
13.如图,⊙O的半径为2,OA,OB是⊙O的半径,P是上任意一点,PE⊥OA于E,PF⊥OB
于F,则EF的最大值为______.
14.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=_____cm.
15.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升______cm.
三、解答题
16.如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于P,求证:.
17.如图,已知AB是⊙O的直径,CD是弦,AE⊥CD,垂足为E,BF⊥CD,垂足为F,且AE=3 cm,BF=5 cm,若⊙O的半径为5 cm,求CD的长.
18.如图,一拱桥所在弧所对的圆心角为120°(即∠AOB=120°),半径为5 m,一艘6 m宽的船装载一集装箱,已知箱顶宽3.2 m,离水面AB高2 m,问此船能过桥洞吗?请说明理由.
19.如图,在⊙O中,AB为直径,且AB⊥CD,垂足为E,CD=,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连结CF,当∠FCD=∠DOB时,直接写出EF的长,并在图中标出F点的具体位置.
20.如图,的半径为5,弦于E,.
求证:;
若于F,于G,试说明四边形OFEG是正方形.
21.如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
参考答案
1.C
【解析】
【分析】
先根据等腰三角形的性质求出∠B=∠A=,再根据三角形的内角和求出∠AOB=,然后由同圆或等圆中相等的弧所对的圆心角相等可得==°.
【详解】
解:∵OA=OB,
∴∠B=∠A=,
∴∠AOB=.
∵点C是的中点,
∴=
∴==°.
故选C.
【点睛】
本题考查了圆心角定理,正确理解圆心角定理是解题的关键.
2.D
【解析】【分析】根据垂径定理,直径所对的角是直角,以及同弧所对的圆周角相等,即可判断.
【详解】∵AB是⊙O的直径,CD为弦,CD⊥AB于E.∴CE=DE.故B成立;
A、根据同弧所对的圆周角相等,得到∠A=∠D,故该选项正确;
C、根据直径所对的圆周角是直角即可得到,故该选项正确;
D、CE=DE,而△BED是直角三角形,则DE<BD,则该项不成立.
故选:D
【点睛】本题主要考查了垂径定理的基本内容,以及直径所对的圆周角是直角.
3.C
【解析】
【分析】
直接利用垂径定理进而结合圆周角定理得出△ODB是等腰直角三角形,进而得出答案.
【详解】
解:∵半径OC⊥弦AB于点D,
∴,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=4,
∴DB=OD=2,
则半径OB等于:.
故选:C.
【点睛】
此题主要考查了垂径定理和圆周角定理,正确得出△ODB是等腰直角三角形是解题关键.
4.D
【解析】
【分析】
要求阴影部分的面积,由图可知,阴影部分的面积等于扇形COB的面积,根据已知条件可以得到扇形COB的面积,本题得以解决.
【详解】
,
,
又弦,,
,
,
故选D.
【点睛】
本题考查了圆周角定理、垂径定理、扇形面积的计算,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
5.C
【解析】
【分析】
根据垂径定理得出弧弧DE,求出弧DE的度数,即可求出答案.
【详解】
解:的直径CD过弦EF的中点G,,
弧弧DE,且弧的度数是,
,
故选:C.
【点睛】
本题考查了圆周角定理,垂径定理的应用,注意:圆心角的度数等于它所对的弧的度数.
6.A
【解析】
【分析】
由垂径定理得,CE= =4,OC=OE+2,由勾股定理得OC2=OE2+CE2,即:(OE+2)2=42+OE2,
再求OE.
【详解】
连接OC,
因为AB是⊙O的直径,AB⊥CD,
所以,CE= =4,OC=OE+2,
在Rt△OCE中,勾股定理得
OC2=OE2+CE2,
即:(OE+2)2=42+OE2,
解得OE=3.
故选:A
【点睛】
本题考核知识点:垂径定理.解题关键点:理解运用垂径定理.
7.B
【解析】【分析】连接OD,由垂径定理得出AB⊥CD,由三角函数求出BH=3,由勾股定理得出DH==4,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
【详解】连接OD,如图所示:
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=∠BHD=90°,
∵sin∠CDB=,BD=5,
∴BH=3,
∴DH==4,
设OH=x,则OD=OB=x+3,
在Rt△ODH中,由勾股定理得:x2+42=(x+3)2,
解得:x=,
∴OH=,
∴AH=OA+OH=+3+=,
故选B.
【点睛】本题考查了垂径定理、勾股定理以及三角函数等知识,正确添加辅助线,熟练应用垂径定理、灵活运用数形结合思想是解题的关键.
8.C
【解析】分析:设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r-1,OA=r,则有r2=52+(r-1)2,解方程即可.
详解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r-1,OA=r,
则有r2=52+(r-1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
点睛:本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题
9.34°
【解析】分析:首先根据垂径定理得出∠BOD的度数,然后根据三角形内角和定理得出∠D的度数.
详解:∵直径AB⊥弦CD, ∴∠BOD=2∠A=56°, ∴∠D=90°-56°=34°.
点睛:本题主要考查的是圆的垂径定理,属于基础题型.求出∠BOD的度数是解题的关键.
10.3
【解析】
【分析】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB,先证四边形OEPF是正方形,得OP=OE,根据垂径定理,BE=AB=4,根据勾股定理:OB=5,BE=4,则OE=3,所以OP=3.
【详解】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB
∵AB⊥CD
∴四边形OEPF是矩形(有3个角是直角的四边形是矩形)
∵AB=CD
∴OE=OF(弦相等,弦心距相等)
∴四边形OEPF是正方形(邻边相等的矩形是正方形)
∴OP=OE(正方形对角线等于倍的边长)
∵OE⊥AB
∴BE=AB=4(垂径定理)
根据勾股定理:OB=5,BE=4
则OE=3
∴OP=3
故答案为:3
【点睛】
本题考核知识点:勾股定理、垂径定理.解题关键点:灵活运用垂径定理和勾股定理.
11.2或14
【解析】分析:分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
详解:①当弦AB和CD在圆心同侧时,如图,
∵AB=16cm,CD=12cm,
∴AE=8cm,CF=6cm,
∵OA=OC=10cm,
∴EO=6cm,OF=8cm,
∴EF=OF-OE=2cm;
②当弦AB和CD在圆心异侧时,如图,
∵AB=16cm,CD=12cm,
∴AF=8cm,CE=6cm,
∵OA=OC=10cm,
∴OF=6cm,OE=8cm,
∴EF=OF+OE=14cm.
∴AB与CD之间的距离为14cm或2cm.
故答案为:2或14.
点睛:本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.
12.4
【解析】
【详解】
如图,作OC垂直弦AB于点C,
∴AC=BC,
∵∠AOB=120°,
∴∠AOC=60°,即∠OAC=30°,
又∵OA=4,
∴OC=OA=2,
∴AB=2AC=2=2=4.
故答案为4.
13.2
【解析】
【分析】
延长PE、PF分别交圆于G、H,根据垂径定理得到PE=EG,PF=FH,得到EF=GH,根据圆的最长的弦是直径解答即可.
【详解】
延长PE、PF分别交圆于G、H,如图所示:
∵PE⊥OA、PF⊥OB, ∴PE=EG,PF=FH ∴EF是△PGH的中位线 ∴EF=GH ∵GH是⊙O的弦 ∴GH的最大值为2OA=2×2=4, ∴EF的最大值为×4=2. 故答案为:2.
【点睛】
考查的是垂径定理、三角形中位线定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14.2
【解析】分析:根据圆心角、弧、弦之间关系求出根据垂径定理得出 根据角平分线性质得出 代入求出即可
详解:∵CD⊥OA,
即OM⊥CD,
由垂径定理得:CD=2CM=4cm,
连接OC,
∵C为弧AB的中点,
∴=,
∴∠AOC=∠BOC,
∵CN⊥OB,CD⊥OA
∴CM=CN=2cm,
故答案为:2.
点睛:圆心角、弧、弦的关系, 角平分线的性质, 垂径定理等,比较基础,熟练掌握各个知识点是解题的关键.
15.10或70
【解析】
【分析】
分水位在圆心下以及圆心上两种情况,画出符合题意的图形进行求解即可得.
【详解】
如图,作半径于C,连接OB,
由垂径定理得:=AB=×60=30cm,
在中,,
当水位上升到圆心以下时??水面宽80cm时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为30cm或70cm,
故答案为:10或70.
【点睛】
本题考查了垂径定理的应用,掌握垂径定理、灵活运用分类讨论的思想是解题的关键.
16.证明见解析
【解析】试题分析:连接OP,根据角平分线的性质以及等腰三角形的性质得出∠DCP=∠P,从而得出CD和OP平行,最后根据垂径定理的逆定理得出答案.
试题解析:连结OP,∵OC=OP,∴∠OCP=∠P,又∠DCP=∠OCP,∴∠DCP=∠P,
∴CD∥OP,∵CD⊥AB,∴OP⊥AB,∴AP=BP
17.6cm
【解析】试题分析:过点O作OH⊥EF,连接OC,首先根据梯形中位线的性质得出OH的长度,然后根据垂径定理得出CH的长度,从而得出CD的长度.
试题解析:过点O作OH⊥EF,连接OC,根据题意可得:OH=(AE+BF)=4cm,
根据Rt△OCH的勾股定理可得:CH=3cm,∴CD=2CH=6cm.
18.能
【解析】试题分析:先根据垂径定理找出圆心O,连接OA,OB,OE,过点OF作OH⊥EF于点H,由∠AOB可得出∠OAB的度数,根据直角三角形的性质得出OK的长,再根据勾股定理得出EH的长,进而得出CD的长与3.2m相比较即可.
试题解析:如图所示,连接OE,过点O作OH⊥EF于点H,
∵∠AOB=120°OA=5m, ∴∠OAB=30°,OK=2.5m,则OH=2.5+2=4.5m,
∵OE=5m, ∴在Rt△OEH中,EH=,
∴EF=2EH=, ∴此船能过桥洞.
点睛:本题主要考查的就是垂径定理的实际应用问题,属于中等难度的题型.在解决这种问题的时候,首先找出圆心,然后根据垂径定理求出未知数的一个量,然后与题目中给出的一个量进行比较大小,从而得出答案.在这种问题的时候,二次函数的实际应用中也会出现,我们一定要分清具体运用哪个知识点来进行求解.
19.(1)r=3;(2)见解析
【解析】分析:(1)、根据垂径定理得出计算出圆的半径;(2)、根据圆心角和圆周角的关系得出∠BCD=∠BOD,作点B关于CD的对称点F,点F即为所求,根据EF=BE得出答案.
详解:解:(1)、∵AB为直径,AB⊥CD, ∴DE=CD=.
在Rt△ODE中, ∵OD=r,OE=5﹣r,DE=, ∴r2=(5﹣r)2+()2,解得r=3;
(2)、如图,连接CB.
∵∠BCD=∠BOD, 作点B关于CD的对称点F,点F即为所求.
∴EF=EB=OB﹣OE=3﹣2=1.
点睛:本题主要考查的就是垂径定理的应用以及圆周角和圆心角之间的关系,属于中等题型.在圆的解答题里面,垂径定理的应用非常广泛,熟练掌握垂径定理是解题的关键.
20.(1)详见解析;(2)四边形OFEG是正方形.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由判断,再得到,从而判断;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到,,则利用得到,然后根据正方形的判定方法可判断四边形OFEG是正方形.
【详解】
(1)证明:,
,
,即,
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
,,,
四边形OFEG是矩形,,.
,
.
,
,
≌,
.
矩形OFEG是正方形
【点睛】
本题考查了圆心角、弧、弦的关系,解题的关键是:熟练掌握垂径定理和圆心角、弧、弦的关系.
21.(1)画图见解析;(2)CE=
【解析】【分析】(1)以点A为圆心,以任意长为半径画弧,分别与AB、AC有交点,再分别以这两个交点为圆心,以大于这两点距离的一半为半径画弧,两弧交于一点,过点A与这点作射线,与圆交于点E ,据此作图即可;
(2)连接OE交BC于点F,连接OC、CE,由AE平分∠BAC,可推导得出OE⊥BC,然后在Rt△OFC中,由勾股定理可求得FC的长,在Rt△EFC中,由勾股定理即可求得CE的长.
【详解】(1)如图所示,射线AE就是所求作的角平分线;
(2)连接OE交BC于点F,连接OC、CE,
∵AE平分∠BAC,
∴,
∴OE⊥BC,EF=3,∴OF=5-3=2,
在Rt△OFC中,由勾股定理可得FC==,
在Rt△EFC中,由勾股定理可得CE==.
【点睛】本题考查了尺规作图——作角平分线,垂径定理等,熟练掌握角平分线的作图方法、推导得出OE⊥BC是解题的关键.
3.3 垂径定理同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.如图,在中,点C是的中点,,则的大小为
A. B. C. D.
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是 ( )
A. ∠A﹦∠D B. CE﹦DE C. ∠ACB﹦90° D. CE﹦BD
3.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A. B. 2 C. 2 D. 3
4.如图,AB是的直径,弦,,,则阴影部分的面积为
A. B. C. D.
5.如图,的直径CD过弦EF的中点G,,则等于
A. B. C. D.
6.如图,AB是⊙O的直径,AB⊥CD于点E,若CD=8,AE=2,则OE长为( )
A. B. C. D.
7.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为( )
A. B. C. D.
8.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A. 13寸 B. 20寸 C. 26寸 D. 28寸
二、填空题
9.如图,在⊙O中,直径AB⊥弦CD,∠A=28°,则∠D=_____.
10.如图,在半径为5cm的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为______.
11.已知的半径为,,是的两条弦,,,,则弦和之间的距离是__________.
12.如图所示,⊙O的半径OA=4,∠AOB=120°,则弦AB长为____________.?
13.如图,⊙O的半径为2,OA,OB是⊙O的半径,P是上任意一点,PE⊥OA于E,PF⊥OB
于F,则EF的最大值为______.
14.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=_____cm.
15.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升______cm.
三、解答题
16.如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于P,求证:.
17.如图,已知AB是⊙O的直径,CD是弦,AE⊥CD,垂足为E,BF⊥CD,垂足为F,且AE=3 cm,BF=5 cm,若⊙O的半径为5 cm,求CD的长.
18.如图,一拱桥所在弧所对的圆心角为120°(即∠AOB=120°),半径为5 m,一艘6 m宽的船装载一集装箱,已知箱顶宽3.2 m,离水面AB高2 m,问此船能过桥洞吗?请说明理由.
19.如图,在⊙O中,AB为直径,且AB⊥CD,垂足为E,CD=,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连结CF,当∠FCD=∠DOB时,直接写出EF的长,并在图中标出F点的具体位置.
20.如图,的半径为5,弦于E,.
求证:;
若于F,于G,试说明四边形OFEG是正方形.
21.如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
参考答案
1.C
【解析】
【分析】
先根据等腰三角形的性质求出∠B=∠A=,再根据三角形的内角和求出∠AOB=,然后由同圆或等圆中相等的弧所对的圆心角相等可得==°.
【详解】
解:∵OA=OB,
∴∠B=∠A=,
∴∠AOB=.
∵点C是的中点,
∴=
∴==°.
故选C.
【点睛】
本题考查了圆心角定理,正确理解圆心角定理是解题的关键.
2.D
【解析】【分析】根据垂径定理,直径所对的角是直角,以及同弧所对的圆周角相等,即可判断.
【详解】∵AB是⊙O的直径,CD为弦,CD⊥AB于E.∴CE=DE.故B成立;
A、根据同弧所对的圆周角相等,得到∠A=∠D,故该选项正确;
C、根据直径所对的圆周角是直角即可得到,故该选项正确;
D、CE=DE,而△BED是直角三角形,则DE<BD,则该项不成立.
故选:D
【点睛】本题主要考查了垂径定理的基本内容,以及直径所对的圆周角是直角.
3.C
【解析】
【分析】
直接利用垂径定理进而结合圆周角定理得出△ODB是等腰直角三角形,进而得出答案.
【详解】
解:∵半径OC⊥弦AB于点D,
∴,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=4,
∴DB=OD=2,
则半径OB等于:.
故选:C.
【点睛】
此题主要考查了垂径定理和圆周角定理,正确得出△ODB是等腰直角三角形是解题关键.
4.D
【解析】
【分析】
要求阴影部分的面积,由图可知,阴影部分的面积等于扇形COB的面积,根据已知条件可以得到扇形COB的面积,本题得以解决.
【详解】
,
,
又弦,,
,
,
故选D.
【点睛】
本题考查了圆周角定理、垂径定理、扇形面积的计算,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
5.C
【解析】
【分析】
根据垂径定理得出弧弧DE,求出弧DE的度数,即可求出答案.
【详解】
解:的直径CD过弦EF的中点G,,
弧弧DE,且弧的度数是,
,
故选:C.
【点睛】
本题考查了圆周角定理,垂径定理的应用,注意:圆心角的度数等于它所对的弧的度数.
6.A
【解析】
【分析】
由垂径定理得,CE= =4,OC=OE+2,由勾股定理得OC2=OE2+CE2,即:(OE+2)2=42+OE2,
再求OE.
【详解】
连接OC,
因为AB是⊙O的直径,AB⊥CD,
所以,CE= =4,OC=OE+2,
在Rt△OCE中,勾股定理得
OC2=OE2+CE2,
即:(OE+2)2=42+OE2,
解得OE=3.
故选:A
【点睛】
本题考核知识点:垂径定理.解题关键点:理解运用垂径定理.
7.B
【解析】【分析】连接OD,由垂径定理得出AB⊥CD,由三角函数求出BH=3,由勾股定理得出DH==4,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
【详解】连接OD,如图所示:
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=∠BHD=90°,
∵sin∠CDB=,BD=5,
∴BH=3,
∴DH==4,
设OH=x,则OD=OB=x+3,
在Rt△ODH中,由勾股定理得:x2+42=(x+3)2,
解得:x=,
∴OH=,
∴AH=OA+OH=+3+=,
故选B.
【点睛】本题考查了垂径定理、勾股定理以及三角函数等知识,正确添加辅助线,熟练应用垂径定理、灵活运用数形结合思想是解题的关键.
8.C
【解析】分析:设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r-1,OA=r,则有r2=52+(r-1)2,解方程即可.
详解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r-1,OA=r,
则有r2=52+(r-1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
点睛:本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题
9.34°
【解析】分析:首先根据垂径定理得出∠BOD的度数,然后根据三角形内角和定理得出∠D的度数.
详解:∵直径AB⊥弦CD, ∴∠BOD=2∠A=56°, ∴∠D=90°-56°=34°.
点睛:本题主要考查的是圆的垂径定理,属于基础题型.求出∠BOD的度数是解题的关键.
10.3
【解析】
【分析】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB,先证四边形OEPF是正方形,得OP=OE,根据垂径定理,BE=AB=4,根据勾股定理:OB=5,BE=4,则OE=3,所以OP=3.
【详解】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB
∵AB⊥CD
∴四边形OEPF是矩形(有3个角是直角的四边形是矩形)
∵AB=CD
∴OE=OF(弦相等,弦心距相等)
∴四边形OEPF是正方形(邻边相等的矩形是正方形)
∴OP=OE(正方形对角线等于倍的边长)
∵OE⊥AB
∴BE=AB=4(垂径定理)
根据勾股定理:OB=5,BE=4
则OE=3
∴OP=3
故答案为:3
【点睛】
本题考核知识点:勾股定理、垂径定理.解题关键点:灵活运用垂径定理和勾股定理.
11.2或14
【解析】分析:分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
详解:①当弦AB和CD在圆心同侧时,如图,
∵AB=16cm,CD=12cm,
∴AE=8cm,CF=6cm,
∵OA=OC=10cm,
∴EO=6cm,OF=8cm,
∴EF=OF-OE=2cm;
②当弦AB和CD在圆心异侧时,如图,
∵AB=16cm,CD=12cm,
∴AF=8cm,CE=6cm,
∵OA=OC=10cm,
∴OF=6cm,OE=8cm,
∴EF=OF+OE=14cm.
∴AB与CD之间的距离为14cm或2cm.
故答案为:2或14.
点睛:本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.
12.4
【解析】
【详解】
如图,作OC垂直弦AB于点C,
∴AC=BC,
∵∠AOB=120°,
∴∠AOC=60°,即∠OAC=30°,
又∵OA=4,
∴OC=OA=2,
∴AB=2AC=2=2=4.
故答案为4.
13.2
【解析】
【分析】
延长PE、PF分别交圆于G、H,根据垂径定理得到PE=EG,PF=FH,得到EF=GH,根据圆的最长的弦是直径解答即可.
【详解】
延长PE、PF分别交圆于G、H,如图所示:
∵PE⊥OA、PF⊥OB, ∴PE=EG,PF=FH ∴EF是△PGH的中位线 ∴EF=GH ∵GH是⊙O的弦 ∴GH的最大值为2OA=2×2=4, ∴EF的最大值为×4=2. 故答案为:2.
【点睛】
考查的是垂径定理、三角形中位线定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14.2
【解析】分析:根据圆心角、弧、弦之间关系求出根据垂径定理得出 根据角平分线性质得出 代入求出即可
详解:∵CD⊥OA,
即OM⊥CD,
由垂径定理得:CD=2CM=4cm,
连接OC,
∵C为弧AB的中点,
∴=,
∴∠AOC=∠BOC,
∵CN⊥OB,CD⊥OA
∴CM=CN=2cm,
故答案为:2.
点睛:圆心角、弧、弦的关系, 角平分线的性质, 垂径定理等,比较基础,熟练掌握各个知识点是解题的关键.
15.10或70
【解析】
【分析】
分水位在圆心下以及圆心上两种情况,画出符合题意的图形进行求解即可得.
【详解】
如图,作半径于C,连接OB,
由垂径定理得:=AB=×60=30cm,
在中,,
当水位上升到圆心以下时??水面宽80cm时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为30cm或70cm,
故答案为:10或70.
【点睛】
本题考查了垂径定理的应用,掌握垂径定理、灵活运用分类讨论的思想是解题的关键.
16.证明见解析
【解析】试题分析:连接OP,根据角平分线的性质以及等腰三角形的性质得出∠DCP=∠P,从而得出CD和OP平行,最后根据垂径定理的逆定理得出答案.
试题解析:连结OP,∵OC=OP,∴∠OCP=∠P,又∠DCP=∠OCP,∴∠DCP=∠P,
∴CD∥OP,∵CD⊥AB,∴OP⊥AB,∴AP=BP
17.6cm
【解析】试题分析:过点O作OH⊥EF,连接OC,首先根据梯形中位线的性质得出OH的长度,然后根据垂径定理得出CH的长度,从而得出CD的长度.
试题解析:过点O作OH⊥EF,连接OC,根据题意可得:OH=(AE+BF)=4cm,
根据Rt△OCH的勾股定理可得:CH=3cm,∴CD=2CH=6cm.
18.能
【解析】试题分析:先根据垂径定理找出圆心O,连接OA,OB,OE,过点OF作OH⊥EF于点H,由∠AOB可得出∠OAB的度数,根据直角三角形的性质得出OK的长,再根据勾股定理得出EH的长,进而得出CD的长与3.2m相比较即可.
试题解析:如图所示,连接OE,过点O作OH⊥EF于点H,
∵∠AOB=120°OA=5m, ∴∠OAB=30°,OK=2.5m,则OH=2.5+2=4.5m,
∵OE=5m, ∴在Rt△OEH中,EH=,
∴EF=2EH=, ∴此船能过桥洞.
点睛:本题主要考查的就是垂径定理的实际应用问题,属于中等难度的题型.在解决这种问题的时候,首先找出圆心,然后根据垂径定理求出未知数的一个量,然后与题目中给出的一个量进行比较大小,从而得出答案.在这种问题的时候,二次函数的实际应用中也会出现,我们一定要分清具体运用哪个知识点来进行求解.
19.(1)r=3;(2)见解析
【解析】分析:(1)、根据垂径定理得出计算出圆的半径;(2)、根据圆心角和圆周角的关系得出∠BCD=∠BOD,作点B关于CD的对称点F,点F即为所求,根据EF=BE得出答案.
详解:解:(1)、∵AB为直径,AB⊥CD, ∴DE=CD=.
在Rt△ODE中, ∵OD=r,OE=5﹣r,DE=, ∴r2=(5﹣r)2+()2,解得r=3;
(2)、如图,连接CB.
∵∠BCD=∠BOD, 作点B关于CD的对称点F,点F即为所求.
∴EF=EB=OB﹣OE=3﹣2=1.
点睛:本题主要考查的就是垂径定理的应用以及圆周角和圆心角之间的关系,属于中等题型.在圆的解答题里面,垂径定理的应用非常广泛,熟练掌握垂径定理是解题的关键.
20.(1)详见解析;(2)四边形OFEG是正方形.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由判断,再得到,从而判断;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到,,则利用得到,然后根据正方形的判定方法可判断四边形OFEG是正方形.
【详解】
(1)证明:,
,
,即,
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
,,,
四边形OFEG是矩形,,.
,
.
,
,
≌,
.
矩形OFEG是正方形
【点睛】
本题考查了圆心角、弧、弦的关系,解题的关键是:熟练掌握垂径定理和圆心角、弧、弦的关系.
21.(1)画图见解析;(2)CE=
【解析】【分析】(1)以点A为圆心,以任意长为半径画弧,分别与AB、AC有交点,再分别以这两个交点为圆心,以大于这两点距离的一半为半径画弧,两弧交于一点,过点A与这点作射线,与圆交于点E ,据此作图即可;
(2)连接OE交BC于点F,连接OC、CE,由AE平分∠BAC,可推导得出OE⊥BC,然后在Rt△OFC中,由勾股定理可求得FC的长,在Rt△EFC中,由勾股定理即可求得CE的长.
【详解】(1)如图所示,射线AE就是所求作的角平分线;
(2)连接OE交BC于点F,连接OC、CE,
∵AE平分∠BAC,
∴,
∴OE⊥BC,EF=3,∴OF=5-3=2,
在Rt△OFC中,由勾股定理可得FC==,
在Rt△EFC中,由勾股定理可得CE==.
【点睛】本题考查了尺规作图——作角平分线,垂径定理等,熟练掌握角平分线的作图方法、推导得出OE⊥BC是解题的关键.
姓名:___________班级:___________考号:___________
一、选择题
1.如图,在中,点C是的中点,,则的大小为
A. B. C. D.
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是 ( )
A. ∠A﹦∠D B. CE﹦DE C. ∠ACB﹦90° D. CE﹦BD
3.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A. B. 2 C. 2 D. 3
4.如图,AB是的直径,弦,,,则阴影部分的面积为
A. B. C. D.
5.如图,的直径CD过弦EF的中点G,,则等于
A. B. C. D.
6.如图,AB是⊙O的直径,AB⊥CD于点E,若CD=8,AE=2,则OE长为( )
A. B. C. D.
7.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为( )
A. B. C. D.
8.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A. 13寸 B. 20寸 C. 26寸 D. 28寸
二、填空题
9.如图,在⊙O中,直径AB⊥弦CD,∠A=28°,则∠D=_____.
10.如图,在半径为5cm的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为______.
11.已知的半径为,,是的两条弦,,,,则弦和之间的距离是__________.
12.如图所示,⊙O的半径OA=4,∠AOB=120°,则弦AB长为____________.?
13.如图,⊙O的半径为2,OA,OB是⊙O的半径,P是上任意一点,PE⊥OA于E,PF⊥OB
于F,则EF的最大值为______.
14.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=_____cm.
15.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升______cm.
三、解答题
16.如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于P,求证:.
17.如图,已知AB是⊙O的直径,CD是弦,AE⊥CD,垂足为E,BF⊥CD,垂足为F,且AE=3 cm,BF=5 cm,若⊙O的半径为5 cm,求CD的长.
18.如图,一拱桥所在弧所对的圆心角为120°(即∠AOB=120°),半径为5 m,一艘6 m宽的船装载一集装箱,已知箱顶宽3.2 m,离水面AB高2 m,问此船能过桥洞吗?请说明理由.
19.如图,在⊙O中,AB为直径,且AB⊥CD,垂足为E,CD=,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连结CF,当∠FCD=∠DOB时,直接写出EF的长,并在图中标出F点的具体位置.
20.如图,的半径为5,弦于E,.
求证:;
若于F,于G,试说明四边形OFEG是正方形.
21.如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
参考答案
1.C
【解析】
【分析】
先根据等腰三角形的性质求出∠B=∠A=,再根据三角形的内角和求出∠AOB=,然后由同圆或等圆中相等的弧所对的圆心角相等可得==°.
【详解】
解:∵OA=OB,
∴∠B=∠A=,
∴∠AOB=.
∵点C是的中点,
∴=
∴==°.
故选C.
【点睛】
本题考查了圆心角定理,正确理解圆心角定理是解题的关键.
2.D
【解析】【分析】根据垂径定理,直径所对的角是直角,以及同弧所对的圆周角相等,即可判断.
【详解】∵AB是⊙O的直径,CD为弦,CD⊥AB于E.∴CE=DE.故B成立;
A、根据同弧所对的圆周角相等,得到∠A=∠D,故该选项正确;
C、根据直径所对的圆周角是直角即可得到,故该选项正确;
D、CE=DE,而△BED是直角三角形,则DE<BD,则该项不成立.
故选:D
【点睛】本题主要考查了垂径定理的基本内容,以及直径所对的圆周角是直角.
3.C
【解析】
【分析】
直接利用垂径定理进而结合圆周角定理得出△ODB是等腰直角三角形,进而得出答案.
【详解】
解:∵半径OC⊥弦AB于点D,
∴,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=4,
∴DB=OD=2,
则半径OB等于:.
故选:C.
【点睛】
此题主要考查了垂径定理和圆周角定理,正确得出△ODB是等腰直角三角形是解题关键.
4.D
【解析】
【分析】
要求阴影部分的面积,由图可知,阴影部分的面积等于扇形COB的面积,根据已知条件可以得到扇形COB的面积,本题得以解决.
【详解】
,
,
又弦,,
,
,
故选D.
【点睛】
本题考查了圆周角定理、垂径定理、扇形面积的计算,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
5.C
【解析】
【分析】
根据垂径定理得出弧弧DE,求出弧DE的度数,即可求出答案.
【详解】
解:的直径CD过弦EF的中点G,,
弧弧DE,且弧的度数是,
,
故选:C.
【点睛】
本题考查了圆周角定理,垂径定理的应用,注意:圆心角的度数等于它所对的弧的度数.
6.A
【解析】
【分析】
由垂径定理得,CE= =4,OC=OE+2,由勾股定理得OC2=OE2+CE2,即:(OE+2)2=42+OE2,
再求OE.
【详解】
连接OC,
因为AB是⊙O的直径,AB⊥CD,
所以,CE= =4,OC=OE+2,
在Rt△OCE中,勾股定理得
OC2=OE2+CE2,
即:(OE+2)2=42+OE2,
解得OE=3.
故选:A
【点睛】
本题考核知识点:垂径定理.解题关键点:理解运用垂径定理.
7.B
【解析】【分析】连接OD,由垂径定理得出AB⊥CD,由三角函数求出BH=3,由勾股定理得出DH==4,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
【详解】连接OD,如图所示:
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=∠BHD=90°,
∵sin∠CDB=,BD=5,
∴BH=3,
∴DH==4,
设OH=x,则OD=OB=x+3,
在Rt△ODH中,由勾股定理得:x2+42=(x+3)2,
解得:x=,
∴OH=,
∴AH=OA+OH=+3+=,
故选B.
【点睛】本题考查了垂径定理、勾股定理以及三角函数等知识,正确添加辅助线,熟练应用垂径定理、灵活运用数形结合思想是解题的关键.
8.C
【解析】分析:设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r-1,OA=r,则有r2=52+(r-1)2,解方程即可.
详解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r-1,OA=r,
则有r2=52+(r-1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
点睛:本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题
9.34°
【解析】分析:首先根据垂径定理得出∠BOD的度数,然后根据三角形内角和定理得出∠D的度数.
详解:∵直径AB⊥弦CD, ∴∠BOD=2∠A=56°, ∴∠D=90°-56°=34°.
点睛:本题主要考查的是圆的垂径定理,属于基础题型.求出∠BOD的度数是解题的关键.
10.3
【解析】
【分析】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB,先证四边形OEPF是正方形,得OP=OE,根据垂径定理,BE=AB=4,根据勾股定理:OB=5,BE=4,则OE=3,所以OP=3.
【详解】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB
∵AB⊥CD
∴四边形OEPF是矩形(有3个角是直角的四边形是矩形)
∵AB=CD
∴OE=OF(弦相等,弦心距相等)
∴四边形OEPF是正方形(邻边相等的矩形是正方形)
∴OP=OE(正方形对角线等于倍的边长)
∵OE⊥AB
∴BE=AB=4(垂径定理)
根据勾股定理:OB=5,BE=4
则OE=3
∴OP=3
故答案为:3
【点睛】
本题考核知识点:勾股定理、垂径定理.解题关键点:灵活运用垂径定理和勾股定理.
11.2或14
【解析】分析:分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
详解:①当弦AB和CD在圆心同侧时,如图,
∵AB=16cm,CD=12cm,
∴AE=8cm,CF=6cm,
∵OA=OC=10cm,
∴EO=6cm,OF=8cm,
∴EF=OF-OE=2cm;
②当弦AB和CD在圆心异侧时,如图,
∵AB=16cm,CD=12cm,
∴AF=8cm,CE=6cm,
∵OA=OC=10cm,
∴OF=6cm,OE=8cm,
∴EF=OF+OE=14cm.
∴AB与CD之间的距离为14cm或2cm.
故答案为:2或14.
点睛:本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.
12.4
【解析】
【详解】
如图,作OC垂直弦AB于点C,
∴AC=BC,
∵∠AOB=120°,
∴∠AOC=60°,即∠OAC=30°,
又∵OA=4,
∴OC=OA=2,
∴AB=2AC=2=2=4.
故答案为4.
13.2
【解析】
【分析】
延长PE、PF分别交圆于G、H,根据垂径定理得到PE=EG,PF=FH,得到EF=GH,根据圆的最长的弦是直径解答即可.
【详解】
延长PE、PF分别交圆于G、H,如图所示:
∵PE⊥OA、PF⊥OB, ∴PE=EG,PF=FH ∴EF是△PGH的中位线 ∴EF=GH ∵GH是⊙O的弦 ∴GH的最大值为2OA=2×2=4, ∴EF的最大值为×4=2. 故答案为:2.
【点睛】
考查的是垂径定理、三角形中位线定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14.2
【解析】分析:根据圆心角、弧、弦之间关系求出根据垂径定理得出 根据角平分线性质得出 代入求出即可
详解:∵CD⊥OA,
即OM⊥CD,
由垂径定理得:CD=2CM=4cm,
连接OC,
∵C为弧AB的中点,
∴=,
∴∠AOC=∠BOC,
∵CN⊥OB,CD⊥OA
∴CM=CN=2cm,
故答案为:2.
点睛:圆心角、弧、弦的关系, 角平分线的性质, 垂径定理等,比较基础,熟练掌握各个知识点是解题的关键.
15.10或70
【解析】
【分析】
分水位在圆心下以及圆心上两种情况,画出符合题意的图形进行求解即可得.
【详解】
如图,作半径于C,连接OB,
由垂径定理得:=AB=×60=30cm,
在中,,
当水位上升到圆心以下时??水面宽80cm时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为30cm或70cm,
故答案为:10或70.
【点睛】
本题考查了垂径定理的应用,掌握垂径定理、灵活运用分类讨论的思想是解题的关键.
16.证明见解析
【解析】试题分析:连接OP,根据角平分线的性质以及等腰三角形的性质得出∠DCP=∠P,从而得出CD和OP平行,最后根据垂径定理的逆定理得出答案.
试题解析:连结OP,∵OC=OP,∴∠OCP=∠P,又∠DCP=∠OCP,∴∠DCP=∠P,
∴CD∥OP,∵CD⊥AB,∴OP⊥AB,∴AP=BP
17.6cm
【解析】试题分析:过点O作OH⊥EF,连接OC,首先根据梯形中位线的性质得出OH的长度,然后根据垂径定理得出CH的长度,从而得出CD的长度.
试题解析:过点O作OH⊥EF,连接OC,根据题意可得:OH=(AE+BF)=4cm,
根据Rt△OCH的勾股定理可得:CH=3cm,∴CD=2CH=6cm.
18.能
【解析】试题分析:先根据垂径定理找出圆心O,连接OA,OB,OE,过点OF作OH⊥EF于点H,由∠AOB可得出∠OAB的度数,根据直角三角形的性质得出OK的长,再根据勾股定理得出EH的长,进而得出CD的长与3.2m相比较即可.
试题解析:如图所示,连接OE,过点O作OH⊥EF于点H,
∵∠AOB=120°OA=5m, ∴∠OAB=30°,OK=2.5m,则OH=2.5+2=4.5m,
∵OE=5m, ∴在Rt△OEH中,EH=,
∴EF=2EH=, ∴此船能过桥洞.
点睛:本题主要考查的就是垂径定理的实际应用问题,属于中等难度的题型.在解决这种问题的时候,首先找出圆心,然后根据垂径定理求出未知数的一个量,然后与题目中给出的一个量进行比较大小,从而得出答案.在这种问题的时候,二次函数的实际应用中也会出现,我们一定要分清具体运用哪个知识点来进行求解.
19.(1)r=3;(2)见解析
【解析】分析:(1)、根据垂径定理得出计算出圆的半径;(2)、根据圆心角和圆周角的关系得出∠BCD=∠BOD,作点B关于CD的对称点F,点F即为所求,根据EF=BE得出答案.
详解:解:(1)、∵AB为直径,AB⊥CD, ∴DE=CD=.
在Rt△ODE中, ∵OD=r,OE=5﹣r,DE=, ∴r2=(5﹣r)2+()2,解得r=3;
(2)、如图,连接CB.
∵∠BCD=∠BOD, 作点B关于CD的对称点F,点F即为所求.
∴EF=EB=OB﹣OE=3﹣2=1.
点睛:本题主要考查的就是垂径定理的应用以及圆周角和圆心角之间的关系,属于中等题型.在圆的解答题里面,垂径定理的应用非常广泛,熟练掌握垂径定理是解题的关键.
20.(1)详见解析;(2)四边形OFEG是正方形.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由判断,再得到,从而判断;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到,,则利用得到,然后根据正方形的判定方法可判断四边形OFEG是正方形.
【详解】
(1)证明:,
,
,即,
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
,,,
四边形OFEG是矩形,,.
,
.
,
,
≌,
.
矩形OFEG是正方形
【点睛】
本题考查了圆心角、弧、弦的关系,解题的关键是:熟练掌握垂径定理和圆心角、弧、弦的关系.
21.(1)画图见解析;(2)CE=
【解析】【分析】(1)以点A为圆心,以任意长为半径画弧,分别与AB、AC有交点,再分别以这两个交点为圆心,以大于这两点距离的一半为半径画弧,两弧交于一点,过点A与这点作射线,与圆交于点E ,据此作图即可;
(2)连接OE交BC于点F,连接OC、CE,由AE平分∠BAC,可推导得出OE⊥BC,然后在Rt△OFC中,由勾股定理可求得FC的长,在Rt△EFC中,由勾股定理即可求得CE的长.
【详解】(1)如图所示,射线AE就是所求作的角平分线;
(2)连接OE交BC于点F,连接OC、CE,
∵AE平分∠BAC,
∴,
∴OE⊥BC,EF=3,∴OF=5-3=2,
在Rt△OFC中,由勾股定理可得FC==,
在Rt△EFC中,由勾股定理可得CE==.
【点睛】本题考查了尺规作图——作角平分线,垂径定理等,熟练掌握角平分线的作图方法、推导得出OE⊥BC是解题的关键.
3.3 垂径定理同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.如图,在中,点C是的中点,,则的大小为
A. B. C. D.
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是 ( )
A. ∠A﹦∠D B. CE﹦DE C. ∠ACB﹦90° D. CE﹦BD
3.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A. B. 2 C. 2 D. 3
4.如图,AB是的直径,弦,,,则阴影部分的面积为
A. B. C. D.
5.如图,的直径CD过弦EF的中点G,,则等于
A. B. C. D.
6.如图,AB是⊙O的直径,AB⊥CD于点E,若CD=8,AE=2,则OE长为( )
A. B. C. D.
7.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为( )
A. B. C. D.
8.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A. 13寸 B. 20寸 C. 26寸 D. 28寸
二、填空题
9.如图,在⊙O中,直径AB⊥弦CD,∠A=28°,则∠D=_____.
10.如图,在半径为5cm的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为______.
11.已知的半径为,,是的两条弦,,,,则弦和之间的距离是__________.
12.如图所示,⊙O的半径OA=4,∠AOB=120°,则弦AB长为____________.?
13.如图,⊙O的半径为2,OA,OB是⊙O的半径,P是上任意一点,PE⊥OA于E,PF⊥OB
于F,则EF的最大值为______.
14.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=_____cm.
15.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升______cm.
三、解答题
16.如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于P,求证:.
17.如图,已知AB是⊙O的直径,CD是弦,AE⊥CD,垂足为E,BF⊥CD,垂足为F,且AE=3 cm,BF=5 cm,若⊙O的半径为5 cm,求CD的长.
18.如图,一拱桥所在弧所对的圆心角为120°(即∠AOB=120°),半径为5 m,一艘6 m宽的船装载一集装箱,已知箱顶宽3.2 m,离水面AB高2 m,问此船能过桥洞吗?请说明理由.
19.如图,在⊙O中,AB为直径,且AB⊥CD,垂足为E,CD=,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连结CF,当∠FCD=∠DOB时,直接写出EF的长,并在图中标出F点的具体位置.
20.如图,的半径为5,弦于E,.
求证:;
若于F,于G,试说明四边形OFEG是正方形.
21.如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
参考答案
1.C
【解析】
【分析】
先根据等腰三角形的性质求出∠B=∠A=,再根据三角形的内角和求出∠AOB=,然后由同圆或等圆中相等的弧所对的圆心角相等可得==°.
【详解】
解:∵OA=OB,
∴∠B=∠A=,
∴∠AOB=.
∵点C是的中点,
∴=
∴==°.
故选C.
【点睛】
本题考查了圆心角定理,正确理解圆心角定理是解题的关键.
2.D
【解析】【分析】根据垂径定理,直径所对的角是直角,以及同弧所对的圆周角相等,即可判断.
【详解】∵AB是⊙O的直径,CD为弦,CD⊥AB于E.∴CE=DE.故B成立;
A、根据同弧所对的圆周角相等,得到∠A=∠D,故该选项正确;
C、根据直径所对的圆周角是直角即可得到,故该选项正确;
D、CE=DE,而△BED是直角三角形,则DE<BD,则该项不成立.
故选:D
【点睛】本题主要考查了垂径定理的基本内容,以及直径所对的圆周角是直角.
3.C
【解析】
【分析】
直接利用垂径定理进而结合圆周角定理得出△ODB是等腰直角三角形,进而得出答案.
【详解】
解:∵半径OC⊥弦AB于点D,
∴,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=4,
∴DB=OD=2,
则半径OB等于:.
故选:C.
【点睛】
此题主要考查了垂径定理和圆周角定理,正确得出△ODB是等腰直角三角形是解题关键.
4.D
【解析】
【分析】
要求阴影部分的面积,由图可知,阴影部分的面积等于扇形COB的面积,根据已知条件可以得到扇形COB的面积,本题得以解决.
【详解】
,
,
又弦,,
,
,
故选D.
【点睛】
本题考查了圆周角定理、垂径定理、扇形面积的计算,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
5.C
【解析】
【分析】
根据垂径定理得出弧弧DE,求出弧DE的度数,即可求出答案.
【详解】
解:的直径CD过弦EF的中点G,,
弧弧DE,且弧的度数是,
,
故选:C.
【点睛】
本题考查了圆周角定理,垂径定理的应用,注意:圆心角的度数等于它所对的弧的度数.
6.A
【解析】
【分析】
由垂径定理得,CE= =4,OC=OE+2,由勾股定理得OC2=OE2+CE2,即:(OE+2)2=42+OE2,
再求OE.
【详解】
连接OC,
因为AB是⊙O的直径,AB⊥CD,
所以,CE= =4,OC=OE+2,
在Rt△OCE中,勾股定理得
OC2=OE2+CE2,
即:(OE+2)2=42+OE2,
解得OE=3.
故选:A
【点睛】
本题考核知识点:垂径定理.解题关键点:理解运用垂径定理.
7.B
【解析】【分析】连接OD,由垂径定理得出AB⊥CD,由三角函数求出BH=3,由勾股定理得出DH==4,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
【详解】连接OD,如图所示:
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=∠BHD=90°,
∵sin∠CDB=,BD=5,
∴BH=3,
∴DH==4,
设OH=x,则OD=OB=x+3,
在Rt△ODH中,由勾股定理得:x2+42=(x+3)2,
解得:x=,
∴OH=,
∴AH=OA+OH=+3+=,
故选B.
【点睛】本题考查了垂径定理、勾股定理以及三角函数等知识,正确添加辅助线,熟练应用垂径定理、灵活运用数形结合思想是解题的关键.
8.C
【解析】分析:设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r-1,OA=r,则有r2=52+(r-1)2,解方程即可.
详解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r-1,OA=r,
则有r2=52+(r-1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
点睛:本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题
9.34°
【解析】分析:首先根据垂径定理得出∠BOD的度数,然后根据三角形内角和定理得出∠D的度数.
详解:∵直径AB⊥弦CD, ∴∠BOD=2∠A=56°, ∴∠D=90°-56°=34°.
点睛:本题主要考查的是圆的垂径定理,属于基础题型.求出∠BOD的度数是解题的关键.
10.3
【解析】
【分析】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB,先证四边形OEPF是正方形,得OP=OE,根据垂径定理,BE=AB=4,根据勾股定理:OB=5,BE=4,则OE=3,所以OP=3.
【详解】
过O点作OE⊥AB于E,OF⊥CD于F,连接OB
∵AB⊥CD
∴四边形OEPF是矩形(有3个角是直角的四边形是矩形)
∵AB=CD
∴OE=OF(弦相等,弦心距相等)
∴四边形OEPF是正方形(邻边相等的矩形是正方形)
∴OP=OE(正方形对角线等于倍的边长)
∵OE⊥AB
∴BE=AB=4(垂径定理)
根据勾股定理:OB=5,BE=4
则OE=3
∴OP=3
故答案为:3
【点睛】
本题考核知识点:勾股定理、垂径定理.解题关键点:灵活运用垂径定理和勾股定理.
11.2或14
【解析】分析:分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
详解:①当弦AB和CD在圆心同侧时,如图,
∵AB=16cm,CD=12cm,
∴AE=8cm,CF=6cm,
∵OA=OC=10cm,
∴EO=6cm,OF=8cm,
∴EF=OF-OE=2cm;
②当弦AB和CD在圆心异侧时,如图,
∵AB=16cm,CD=12cm,
∴AF=8cm,CE=6cm,
∵OA=OC=10cm,
∴OF=6cm,OE=8cm,
∴EF=OF+OE=14cm.
∴AB与CD之间的距离为14cm或2cm.
故答案为:2或14.
点睛:本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.
12.4
【解析】
【详解】
如图,作OC垂直弦AB于点C,
∴AC=BC,
∵∠AOB=120°,
∴∠AOC=60°,即∠OAC=30°,
又∵OA=4,
∴OC=OA=2,
∴AB=2AC=2=2=4.
故答案为4.
13.2
【解析】
【分析】
延长PE、PF分别交圆于G、H,根据垂径定理得到PE=EG,PF=FH,得到EF=GH,根据圆的最长的弦是直径解答即可.
【详解】
延长PE、PF分别交圆于G、H,如图所示:
∵PE⊥OA、PF⊥OB, ∴PE=EG,PF=FH ∴EF是△PGH的中位线 ∴EF=GH ∵GH是⊙O的弦 ∴GH的最大值为2OA=2×2=4, ∴EF的最大值为×4=2. 故答案为:2.
【点睛】
考查的是垂径定理、三角形中位线定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14.2
【解析】分析:根据圆心角、弧、弦之间关系求出根据垂径定理得出 根据角平分线性质得出 代入求出即可
详解:∵CD⊥OA,
即OM⊥CD,
由垂径定理得:CD=2CM=4cm,
连接OC,
∵C为弧AB的中点,
∴=,
∴∠AOC=∠BOC,
∵CN⊥OB,CD⊥OA
∴CM=CN=2cm,
故答案为:2.
点睛:圆心角、弧、弦的关系, 角平分线的性质, 垂径定理等,比较基础,熟练掌握各个知识点是解题的关键.
15.10或70
【解析】
【分析】
分水位在圆心下以及圆心上两种情况,画出符合题意的图形进行求解即可得.
【详解】
如图,作半径于C,连接OB,
由垂径定理得:=AB=×60=30cm,
在中,,
当水位上升到圆心以下时??水面宽80cm时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为30cm或70cm,
故答案为:10或70.
【点睛】
本题考查了垂径定理的应用,掌握垂径定理、灵活运用分类讨论的思想是解题的关键.
16.证明见解析
【解析】试题分析:连接OP,根据角平分线的性质以及等腰三角形的性质得出∠DCP=∠P,从而得出CD和OP平行,最后根据垂径定理的逆定理得出答案.
试题解析:连结OP,∵OC=OP,∴∠OCP=∠P,又∠DCP=∠OCP,∴∠DCP=∠P,
∴CD∥OP,∵CD⊥AB,∴OP⊥AB,∴AP=BP
17.6cm
【解析】试题分析:过点O作OH⊥EF,连接OC,首先根据梯形中位线的性质得出OH的长度,然后根据垂径定理得出CH的长度,从而得出CD的长度.
试题解析:过点O作OH⊥EF,连接OC,根据题意可得:OH=(AE+BF)=4cm,
根据Rt△OCH的勾股定理可得:CH=3cm,∴CD=2CH=6cm.
18.能
【解析】试题分析:先根据垂径定理找出圆心O,连接OA,OB,OE,过点OF作OH⊥EF于点H,由∠AOB可得出∠OAB的度数,根据直角三角形的性质得出OK的长,再根据勾股定理得出EH的长,进而得出CD的长与3.2m相比较即可.
试题解析:如图所示,连接OE,过点O作OH⊥EF于点H,
∵∠AOB=120°OA=5m, ∴∠OAB=30°,OK=2.5m,则OH=2.5+2=4.5m,
∵OE=5m, ∴在Rt△OEH中,EH=,
∴EF=2EH=, ∴此船能过桥洞.
点睛:本题主要考查的就是垂径定理的实际应用问题,属于中等难度的题型.在解决这种问题的时候,首先找出圆心,然后根据垂径定理求出未知数的一个量,然后与题目中给出的一个量进行比较大小,从而得出答案.在这种问题的时候,二次函数的实际应用中也会出现,我们一定要分清具体运用哪个知识点来进行求解.
19.(1)r=3;(2)见解析
【解析】分析:(1)、根据垂径定理得出计算出圆的半径;(2)、根据圆心角和圆周角的关系得出∠BCD=∠BOD,作点B关于CD的对称点F,点F即为所求,根据EF=BE得出答案.
详解:解:(1)、∵AB为直径,AB⊥CD, ∴DE=CD=.
在Rt△ODE中, ∵OD=r,OE=5﹣r,DE=, ∴r2=(5﹣r)2+()2,解得r=3;
(2)、如图,连接CB.
∵∠BCD=∠BOD, 作点B关于CD的对称点F,点F即为所求.
∴EF=EB=OB﹣OE=3﹣2=1.
点睛:本题主要考查的就是垂径定理的应用以及圆周角和圆心角之间的关系,属于中等题型.在圆的解答题里面,垂径定理的应用非常广泛,熟练掌握垂径定理是解题的关键.
20.(1)详见解析;(2)四边形OFEG是正方形.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由判断,再得到,从而判断;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到,,则利用得到,然后根据正方形的判定方法可判断四边形OFEG是正方形.
【详解】
(1)证明:,
,
,即,
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
,,,
四边形OFEG是矩形,,.
,
.
,
,
≌,
.
矩形OFEG是正方形
【点睛】
本题考查了圆心角、弧、弦的关系,解题的关键是:熟练掌握垂径定理和圆心角、弧、弦的关系.
21.(1)画图见解析;(2)CE=
【解析】【分析】(1)以点A为圆心,以任意长为半径画弧,分别与AB、AC有交点,再分别以这两个交点为圆心,以大于这两点距离的一半为半径画弧,两弧交于一点,过点A与这点作射线,与圆交于点E ,据此作图即可;
(2)连接OE交BC于点F,连接OC、CE,由AE平分∠BAC,可推导得出OE⊥BC,然后在Rt△OFC中,由勾股定理可求得FC的长,在Rt△EFC中,由勾股定理即可求得CE的长.
【详解】(1)如图所示,射线AE就是所求作的角平分线;
(2)连接OE交BC于点F,连接OC、CE,
∵AE平分∠BAC,
∴,
∴OE⊥BC,EF=3,∴OF=5-3=2,
在Rt△OFC中,由勾股定理可得FC==,
在Rt△EFC中,由勾股定理可得CE==.
【点睛】本题考查了尺规作图——作角平分线,垂径定理等,熟练掌握角平分线的作图方法、推导得出OE⊥BC是解题的关键.
同课章节目录
