3.3 垂径定理同步课时作业(2)
图片预览




文档简介
3.3 垂径定理同步课时作业(2)
姓名:___________班级:___________考号:___________
一、选择题
1.下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,其中是假命题的是( )
A. ①②?③④ B. ①③?②④ C. ①④?②③ D. ②③?①④
3.如图,CD是⊙O的直径,弦AB⊥CD于点E,连接BC,BD,下列结论中不一定正确的是( )
A. AE=BE B. C. OE=DE D. ∠DBC=90°
4.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
A. 10cm B. 10cm C. 10cm D. 8cm
5.如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F,已知BC=8,DE=2,则⊙O的半径为( )
A. 8 B. 5 C. 2.5 D. 6
6.如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
A. AE的垂直平分线与AC的垂直平分线的交点 B. AB的垂直平分线与AC的垂直平分线的交点
C. AE的垂直平分线与BC的垂直平分线的交点 D. AB的垂直平分线与BC的垂直平分线的交点
7.如图,⊙的直径, 是圆上任一点(、除外),的平分线交⊙于,弦过、的中点、,则的长是( )
A. B. C. D.
8.如图, 是半圆的直径, 为弦, 于,过点作交半圆于点,过点作于,若,则的长为( )
A. B. C. D.
9.如图,圆O过点B、C,圆心O在正△ABC的内部,AB=2, OC=1,则圆O的半径为( )
A. ?????B. 2???? ? C. ?? D.
二、填空题
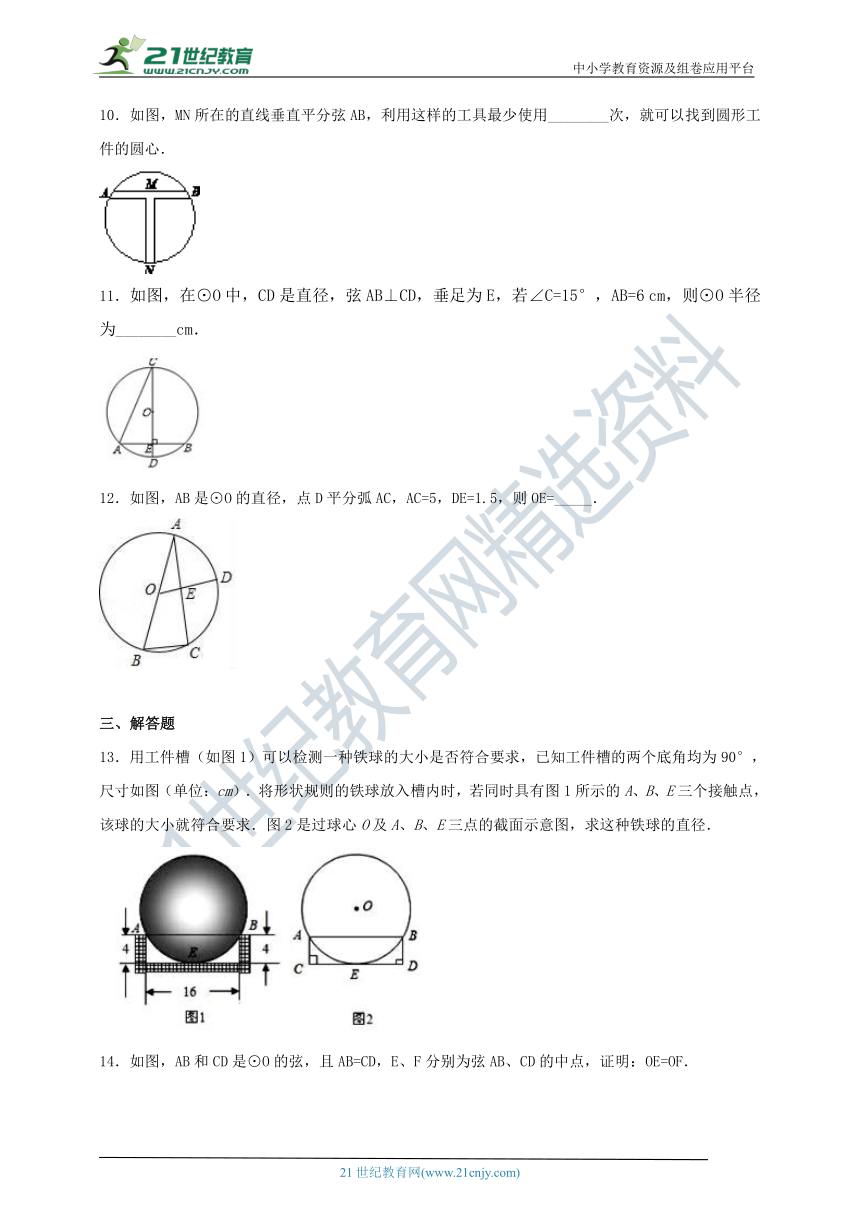
10.如图,MN所在的直线垂直平分弦AB,利用这样的工具最少使用________次,就可以找到圆形工件的圆心.
11.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=6 cm,则⊙O半径为________cm.
12.如图,AB是⊙O的直径,点D平分弧AC,AC=5,DE=1.5,则OE=_____.
三、解答题
13.用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.
14.如图,AB和CD是⊙O的弦,且AB=CD,E、F分别为弦AB、CD的中点,证明:OE=OF.
15.如图所示,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F.若CF⊥AD,AB=2,求CD的长.
16.如图,AB是半圆的直径,0是圆心,C是半圆上一点,D是弧AC的中点,0D交弦AC于E,连接BE.若AC=8,DE=2,求BE的长度.
参考答案
1.B
【解析】试题解析:(l)垂直于弦的直径平分弦,故本选项错误;
(2)平分弦(不是直径)的直径必垂直于弦,并且平分弦所对的两条弧,故本选项错误;
(3)垂直于弦且平分弦的直线必过圆心,故本选项错误;
(4)弦所对的两条弧的中点连线垂直平分弦.故本选项正确;
其中正确的命题有1个.
故选A.
2.B
【解析】试题分析:垂直与弦的直径平分弦,并且平分弦所对的弧;连接弦所对的两条弧的中点的直线垂直与弦,且经过圆心;垂直平分弦的直线必过圆心,且平分弦所对的弧,故本题选B.
3.C
【解析】∵CD⊥AB,CD是⊙O的直径,AB是弦,
∴AE=BE,弧 AD=弧BD,∠DBC=90°,
∴AD=BD,
∴A、B、D正确.
无法说明OE=DE,故C不一定正确.
故选C.
4.B
【解析】根据垂径定理及推论,作弦心距,构造直角三角形,根据勾股定理求解.
解:如图,过点O作OH⊥EF交EF于H.
设OF=xcm, 由题意知,⊙O和BC相切,则H,O,G三点在一条直线上. ∵EF=CD=16 根据垂定定理得HF=8, 在RtΔOHF中,
OF2=OH2+HF2,
x2=82+(16-x)2解得x=10 故选B.
“点睛”解本题的关键是作辅助线弦心距,构造直角三角形,这个直角三角形的斜边是半径,另两条边分别为弦心距和弦的一半,再根据解直角三角形解题.
5.B
【解析】分析:设⊙O的半径为x,根据垂径定理的逆定理可得OD⊥BC,DC=BC=4,在Rt△ODC中,根据勾股定理列出方程,解方程求得x的值,即可得⊙O的半径的长.
详解:
设⊙O的半径为x,
∵E点是的中点,O点是圆心,
∴OD⊥BC,DC=BC=4,
在Rt△ODC中,OD=x﹣2,
∴OD2+DC2=OC2
∴(x﹣2)2+42=x2
∴x=5,即⊙O的半径为5;
故选B.
点睛:本题考查了垂径定理的推论:过圆心平分弧的直径垂直平分弦(不是直径).也考查了勾股定理和方程思想.
6.C
【解析】连接AD,作AE的中垂线交AD于O,连接OE,
∵AB=AC,D是边BC的中点,∴AD⊥BC,∴AD是BC的中垂线,
∵BC是圆的切线,∴AD必过圆心,
∵AE是圆的弦,∴AE的中垂线必过圆心,
∴该圆的圆心是线段AE的中垂线与线段BC的中垂线的交点,故选C.
7.A
【解析】∵是的角平分线,
∴,
∴弧弧,
∴,
又∵是直径,
∴,即为等腰直角三角形.
连接,交于点,则,
∵, 是, 的中点,
∴,
∴, ,
连接根据勾股定理,得
, .
故答案为: .
故选.
8.C
【解析】∵, ,
∴,
∵, ,
∴,
∵,
∴,
∴, ,
∴,
在和中,
,
∴≌,
∴.
故选.
9.D
【解析】试题解析:延长CO交AB于点D,连接OA,OB.
∵△ABC为正三角形, ∴CA=CB,∵CO=CO,OA=OB, ∴△ACO≌△BCO, ∴∠ACO=∠BCO,∵CA=CB, ∴CD⊥AB, ∵AB=2, ∴AD=, ∴CD=3, ∵OC=1, ∴OD=2, ∴OA=, 故选D.
10.2
【解析】分析:根据垂径定理的推论可得,MN所在直线是直径的位置,而两个直径的交点即为圆心,故最少使用2次就可以找到圆形工件的圆心.
详解:如图所示,
根据垂径定理的推论,两个直径的交点即为圆心. 故利用这样的工具最少使用2.次.
故答案为:2.
点睛:此题主要考查垂径定理的推论:弦的垂直平分线经过圆心,并且平分这条弦所对的弧.
11.6
【解析】试题解析:连接OA,如图所示
则∠AOE=2∠C=30°,
∵AB⊥CD,
∴AE=BE=AB=3cm,
∴OA=2OE=6cm,
即⊙O半径为6cm.
12.
【解析】分析:根据平分弦所对一条弧的直径,垂直平分弦,可得OE⊥AC,AE=AC,设OE=x,在Rt△OAE中根据勾股定理列出方程求解即可.
详解:∵点D平分弧AC,OD为半径,
∴OE⊥AC,AE=AC=2.5,
设OE=x,则OA=OD=1.5+x,
在Rt△OAE中由勾股定理得:
2.52+x2=(1.5+x)2,
解得:x=,
即OE=.
故答案为:.
点睛:本题主要考查了垂径定理的推论:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.根据推论构造出直角三角形是解决此题的关键.
13.20㎝.
【解析】试题分析:连接OA、OE,设OE与AB交于点P,根据题意得出四边形ABCD为矩形,根据垂径定理得出PA=8cm,PE=4cm,然后根据Rt△AOP的勾股定理求出OA的值,从而得出圆的直径.
试题解析:连接OA、OE,设OE与AB交于点P,如图
∵AC=BD,AC⊥CD,BD⊥CD
∴四边形ACDB是矩形
∵CD=16cm,PE=4cm
∴PA=8cm,BP=8cm,
在Rt△OAP中,由勾股定理得OA2=PA2+OP2
即OA2=82+(OA﹣4)2
解得:OA=10.
答:这种铁球的直径为20cm.
14.证明见解析.
【解析】试题分析: 根据平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧得到OE⊥AB,AE=BE,OF⊥CD,CF=DF,由于AB=CD,则AE=CF,然后根据“HL”可判断Rt△AEO≌Rt△COF,于是得到OE=OF.
试题解析:
证明:连结OA、OC,如图,
∵E、F分别为弦AB、CD的中点,
∴OE⊥AB,AE=BE,OF⊥CD,CF=DF,
∵AB=CD,
∴AE=CF,
在Rt△AEO和Rt△COF中,
,
∴Rt△AEO≌Rt△COF(HL),
∴OE=OF.
15..
【解析】试题分析:由AB⊥CD,CF⊥AD,根据垂径定理判定△ACD为等边三角形,然后根据边角关系求出DE的长,进而求出CD的长.
解:连接AC
∵AB⊥CD
∴CE=DE(垂径分弦)
∴AB垂直平分CD
∴AC=AD,
∵CF⊥AD, ∴AF=DF(垂径分弦),
∴CF垂直平分AD,
∴AC=CD,
∴AC=AD=CD,
∴△ACD为等边三角形,
∴∠DCF=∠ACD=30°,
∵CO=AO=AB=1,
∴DE=CE=CO×=;
∴CD=2DE=.
点睛:本题主要考查了圆中的垂径定理的应用,解直角三角形以及等边三角形的性质;根据题意由垂径定理判定△ACD为等边三角形是解题的关键;本题中用到了圆与三角形的性质,属于中等题型.
16.
【解析】试题分析:连接BC,设OD=OA=x,在Rt△AEO中,根据 求出x的值,在Rt△ABC中求出BC的长度,再Rt△CBE中求BE的长度;
试题解析:
解:如图,连接BC
D是弧AC的中点
OD垂直平分AC
EA=EC=
设OD=OA=x,则OE=x-2,
即,
解得x=5
AB=2OA=10
答:BE的长度为.
姓名:___________班级:___________考号:___________
一、选择题
1.下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,其中是假命题的是( )
A. ①②?③④ B. ①③?②④ C. ①④?②③ D. ②③?①④
3.如图,CD是⊙O的直径,弦AB⊥CD于点E,连接BC,BD,下列结论中不一定正确的是( )
A. AE=BE B. C. OE=DE D. ∠DBC=90°
4.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
A. 10cm B. 10cm C. 10cm D. 8cm
5.如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F,已知BC=8,DE=2,则⊙O的半径为( )
A. 8 B. 5 C. 2.5 D. 6
6.如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
A. AE的垂直平分线与AC的垂直平分线的交点 B. AB的垂直平分线与AC的垂直平分线的交点
C. AE的垂直平分线与BC的垂直平分线的交点 D. AB的垂直平分线与BC的垂直平分线的交点
7.如图,⊙的直径, 是圆上任一点(、除外),的平分线交⊙于,弦过、的中点、,则的长是( )
A. B. C. D.
8.如图, 是半圆的直径, 为弦, 于,过点作交半圆于点,过点作于,若,则的长为( )
A. B. C. D.
9.如图,圆O过点B、C,圆心O在正△ABC的内部,AB=2, OC=1,则圆O的半径为( )
A. ?????B. 2???? ? C. ?? D.
二、填空题
10.如图,MN所在的直线垂直平分弦AB,利用这样的工具最少使用________次,就可以找到圆形工件的圆心.
11.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=6 cm,则⊙O半径为________cm.
12.如图,AB是⊙O的直径,点D平分弧AC,AC=5,DE=1.5,则OE=_____.
三、解答题
13.用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.
14.如图,AB和CD是⊙O的弦,且AB=CD,E、F分别为弦AB、CD的中点,证明:OE=OF.
15.如图所示,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F.若CF⊥AD,AB=2,求CD的长.
16.如图,AB是半圆的直径,0是圆心,C是半圆上一点,D是弧AC的中点,0D交弦AC于E,连接BE.若AC=8,DE=2,求BE的长度.
参考答案
1.B
【解析】试题解析:(l)垂直于弦的直径平分弦,故本选项错误;
(2)平分弦(不是直径)的直径必垂直于弦,并且平分弦所对的两条弧,故本选项错误;
(3)垂直于弦且平分弦的直线必过圆心,故本选项错误;
(4)弦所对的两条弧的中点连线垂直平分弦.故本选项正确;
其中正确的命题有1个.
故选A.
2.B
【解析】试题分析:垂直与弦的直径平分弦,并且平分弦所对的弧;连接弦所对的两条弧的中点的直线垂直与弦,且经过圆心;垂直平分弦的直线必过圆心,且平分弦所对的弧,故本题选B.
3.C
【解析】∵CD⊥AB,CD是⊙O的直径,AB是弦,
∴AE=BE,弧 AD=弧BD,∠DBC=90°,
∴AD=BD,
∴A、B、D正确.
无法说明OE=DE,故C不一定正确.
故选C.
4.B
【解析】根据垂径定理及推论,作弦心距,构造直角三角形,根据勾股定理求解.
解:如图,过点O作OH⊥EF交EF于H.
设OF=xcm, 由题意知,⊙O和BC相切,则H,O,G三点在一条直线上. ∵EF=CD=16 根据垂定定理得HF=8, 在RtΔOHF中,
OF2=OH2+HF2,
x2=82+(16-x)2解得x=10 故选B.
“点睛”解本题的关键是作辅助线弦心距,构造直角三角形,这个直角三角形的斜边是半径,另两条边分别为弦心距和弦的一半,再根据解直角三角形解题.
5.B
【解析】分析:设⊙O的半径为x,根据垂径定理的逆定理可得OD⊥BC,DC=BC=4,在Rt△ODC中,根据勾股定理列出方程,解方程求得x的值,即可得⊙O的半径的长.
详解:
设⊙O的半径为x,
∵E点是的中点,O点是圆心,
∴OD⊥BC,DC=BC=4,
在Rt△ODC中,OD=x﹣2,
∴OD2+DC2=OC2
∴(x﹣2)2+42=x2
∴x=5,即⊙O的半径为5;
故选B.
点睛:本题考查了垂径定理的推论:过圆心平分弧的直径垂直平分弦(不是直径).也考查了勾股定理和方程思想.
6.C
【解析】连接AD,作AE的中垂线交AD于O,连接OE,
∵AB=AC,D是边BC的中点,∴AD⊥BC,∴AD是BC的中垂线,
∵BC是圆的切线,∴AD必过圆心,
∵AE是圆的弦,∴AE的中垂线必过圆心,
∴该圆的圆心是线段AE的中垂线与线段BC的中垂线的交点,故选C.
7.A
【解析】∵是的角平分线,
∴,
∴弧弧,
∴,
又∵是直径,
∴,即为等腰直角三角形.
连接,交于点,则,
∵, 是, 的中点,
∴,
∴, ,
连接根据勾股定理,得
, .
故答案为: .
故选.
8.C
【解析】∵, ,
∴,
∵, ,
∴,
∵,
∴,
∴, ,
∴,
在和中,
,
∴≌,
∴.
故选.
9.D
【解析】试题解析:延长CO交AB于点D,连接OA,OB.
∵△ABC为正三角形, ∴CA=CB,∵CO=CO,OA=OB, ∴△ACO≌△BCO, ∴∠ACO=∠BCO,∵CA=CB, ∴CD⊥AB, ∵AB=2, ∴AD=, ∴CD=3, ∵OC=1, ∴OD=2, ∴OA=, 故选D.
10.2
【解析】分析:根据垂径定理的推论可得,MN所在直线是直径的位置,而两个直径的交点即为圆心,故最少使用2次就可以找到圆形工件的圆心.
详解:如图所示,
根据垂径定理的推论,两个直径的交点即为圆心. 故利用这样的工具最少使用2.次.
故答案为:2.
点睛:此题主要考查垂径定理的推论:弦的垂直平分线经过圆心,并且平分这条弦所对的弧.
11.6
【解析】试题解析:连接OA,如图所示
则∠AOE=2∠C=30°,
∵AB⊥CD,
∴AE=BE=AB=3cm,
∴OA=2OE=6cm,
即⊙O半径为6cm.
12.
【解析】分析:根据平分弦所对一条弧的直径,垂直平分弦,可得OE⊥AC,AE=AC,设OE=x,在Rt△OAE中根据勾股定理列出方程求解即可.
详解:∵点D平分弧AC,OD为半径,
∴OE⊥AC,AE=AC=2.5,
设OE=x,则OA=OD=1.5+x,
在Rt△OAE中由勾股定理得:
2.52+x2=(1.5+x)2,
解得:x=,
即OE=.
故答案为:.
点睛:本题主要考查了垂径定理的推论:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.根据推论构造出直角三角形是解决此题的关键.
13.20㎝.
【解析】试题分析:连接OA、OE,设OE与AB交于点P,根据题意得出四边形ABCD为矩形,根据垂径定理得出PA=8cm,PE=4cm,然后根据Rt△AOP的勾股定理求出OA的值,从而得出圆的直径.
试题解析:连接OA、OE,设OE与AB交于点P,如图
∵AC=BD,AC⊥CD,BD⊥CD
∴四边形ACDB是矩形
∵CD=16cm,PE=4cm
∴PA=8cm,BP=8cm,
在Rt△OAP中,由勾股定理得OA2=PA2+OP2
即OA2=82+(OA﹣4)2
解得:OA=10.
答:这种铁球的直径为20cm.
14.证明见解析.
【解析】试题分析: 根据平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧得到OE⊥AB,AE=BE,OF⊥CD,CF=DF,由于AB=CD,则AE=CF,然后根据“HL”可判断Rt△AEO≌Rt△COF,于是得到OE=OF.
试题解析:
证明:连结OA、OC,如图,
∵E、F分别为弦AB、CD的中点,
∴OE⊥AB,AE=BE,OF⊥CD,CF=DF,
∵AB=CD,
∴AE=CF,
在Rt△AEO和Rt△COF中,
,
∴Rt△AEO≌Rt△COF(HL),
∴OE=OF.
15..
【解析】试题分析:由AB⊥CD,CF⊥AD,根据垂径定理判定△ACD为等边三角形,然后根据边角关系求出DE的长,进而求出CD的长.
解:连接AC
∵AB⊥CD
∴CE=DE(垂径分弦)
∴AB垂直平分CD
∴AC=AD,
∵CF⊥AD, ∴AF=DF(垂径分弦),
∴CF垂直平分AD,
∴AC=CD,
∴AC=AD=CD,
∴△ACD为等边三角形,
∴∠DCF=∠ACD=30°,
∵CO=AO=AB=1,
∴DE=CE=CO×=;
∴CD=2DE=.
点睛:本题主要考查了圆中的垂径定理的应用,解直角三角形以及等边三角形的性质;根据题意由垂径定理判定△ACD为等边三角形是解题的关键;本题中用到了圆与三角形的性质,属于中等题型.
16.
【解析】试题分析:连接BC,设OD=OA=x,在Rt△AEO中,根据 求出x的值,在Rt△ABC中求出BC的长度,再Rt△CBE中求BE的长度;
试题解析:
解:如图,连接BC
D是弧AC的中点
OD垂直平分AC
EA=EC=
设OD=OA=x,则OE=x-2,
即,
解得x=5
AB=2OA=10
答:BE的长度为.
同课章节目录
