3.4 圆心角同步课时作业(1)
图片预览




文档简介
3.4 圆心角同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.下列语句中正确的是( )
A. 长度相等的两条弧是等弧 B. 平分弦的直径垂直于弦
C. 相等的圆心角所对的弧相等 D. 经过圆心的每一条直线都是圆的对称轴
2.如图,已知AB是☉O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE=( )
A. 40° B. 60° C. 80° D. 120°
3.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. = B. > C. < D. 不能确定
4.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A. 6 B. 8 C. 5 D. 5
5.如图,在半径为R的⊙O中,和度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).
A. R B. C. 2R D. 3R
6.如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )
A. OE=OF B. 弧AC=弧BD C. AC=CD=DB D. CD∥AB
7.如图,AB是⊙O的直径, ,∠COD=38°,则∠AEO的度数是( )
A. 52° B. 57° C. 66° D. 78°
8.如图,AB和CD是⊙O的两条直径,弦DE∥AB,若∠DOE=40°的弧,则∠BOC=( )
A. 110° B. 80° C. 40° D. 70°
二、填空题
9.如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是BC弧的中点,则∠ACD=?________.
?
10.如图,⊙O中,已知弧AB=弧BC,且弧AB:弧AmC=3:4,则∠AOC=________度.
11.如图,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=35°,则∠AOE=________?°.
12.如图,⊙经过五边形的四个顶点,若, , ,则的度数为__________.
13.如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC的度数为______°.
14.如图,已知AB是⊙O的直径,C、D、E、F、G是上的点,且有,则∠OCG=___.
15.如图,MN是⊙O的直径,OM=2,点A在⊙O上, ,B为弧AN的中点, P是直径MN上一动点,则PA+PB的最小值为 ______________.
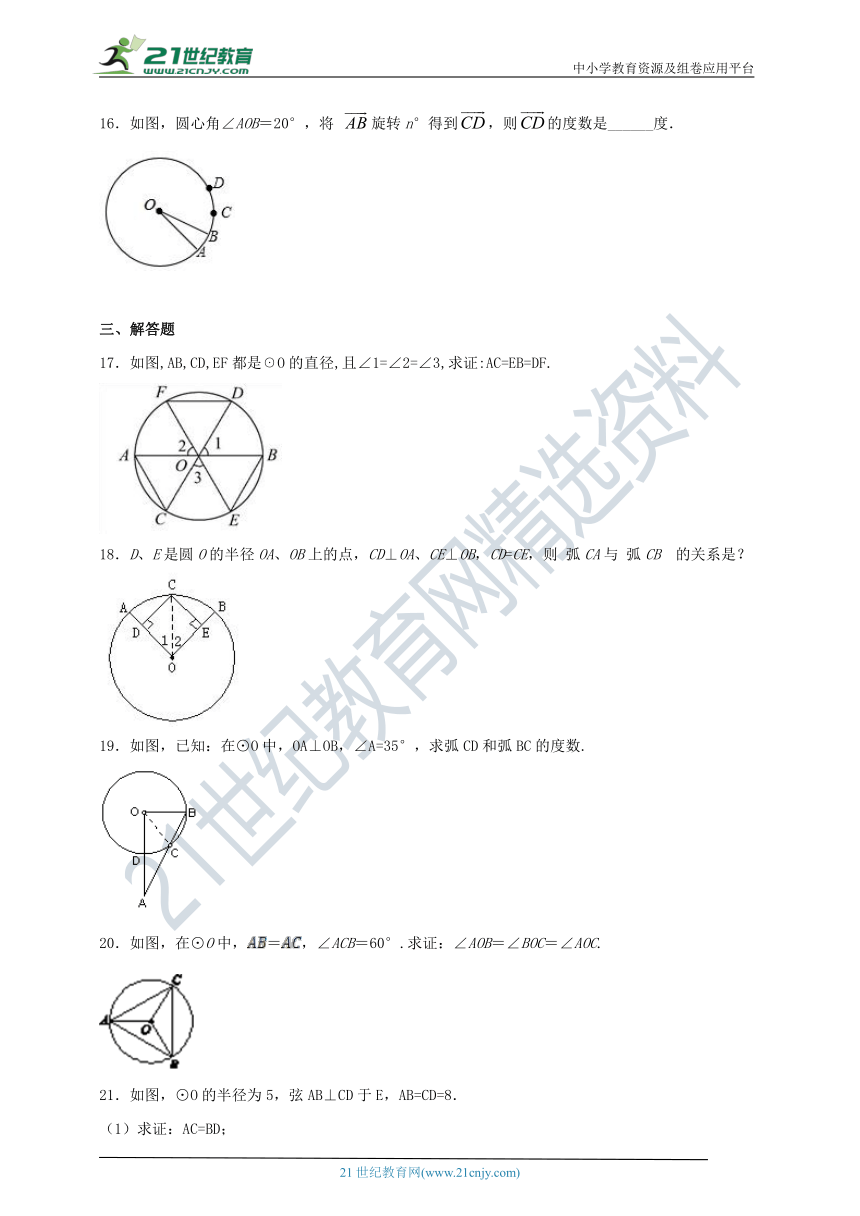
16.如图,圆心角∠AOB=20°,将 旋转n°得到,则的度数是______度.
三、解答题
17.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
18.D、E是圆O的半径OA、OB上的点,CD⊥OA、CE⊥OB,CD=CE,则 弧CA与 弧CB?的关系是?
19.如图,已知:在⊙O中,OA⊥OB,∠A=35°,求弧CD和弧BC的度数.
20.如图,在⊙O中,=,∠ACB=60°.求证:∠AOB=∠BOC=∠AOC.
21.如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
22.如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
参考答案
1.D
【解析】分析:根据垂径定理及逆定理以及圆的性质来进行判定分析即可得出答案.
详解:A、在同圆或等圆中,长度相等的两条弧是等弧;B、平分弦(不是直径)的直径垂直于弦;C、在同圆或等圆中,相等的圆心角所对的弧相等;D、经过圆心的每一条直线都是圆的对称轴;故选D.
点睛:本题主要考查的是圆的一些基本性质,属于基础题型.理解圆的性质是解决这个问题的关键.
2.B
【解析】
【分析】
根据等弧所对的圆心角相等求得∠EOD=∠COD=∠BOC,从而可求得∠AOE的度数.
【详解】
∵D、C是劣弧EB的三等分点,∠BOC=40°?,
∴∠EOD=∠COD=∠BOC=40°?,
∴∠AOE=60°.?
故选B.
【点睛】
本题考查了同弧所对的圆心角相等.由D,C是劣弧EB的三等分点求得∠EOD=∠COD=∠BOC是解答本题的关键.
3.D
【解析】分析:根据在同圆和等圆中相等的弦所对的弧相等分析,从而得到答案.
详解:在同圆和等圆中相等的弦所对的弧才会相等,要注意同圆和等圆的条件,本题是两个不同的圆,所以无法判断两弦所对的弧的大小,
故选D.
点睛:本题考查了在同圆和等圆中相等的弦所对的弧相等的理解及运用,解题的关键是不要忽视在同圆或等圆中这一前提条件.
4.B
【解析】【分析】延长AO交⊙O于点E,连接BE,由∠AOB+∠BOE=∠AOB+∠COD知∠BOE=∠COD,据此可得BE=CD=6,在Rt△ABE中利用勾股定理求解可得.
【详解】如图,延长AO交⊙O于点E,连接BE,
则∠AOB+∠BOE=180°,
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6,
∵AE为⊙O的直径,
∴∠ABE=90°,
∴AB==8,
故选B.
【点睛】本题考查了弧、弦、圆心角的关系,圆周角定理等,正确添加辅助线以及熟练应用相关的性质与定理是解题的关键.
5.A
【解析】分析:如解答图,作辅助线,构造三个等腰三角形△OAB,△OCD与△OCE;证明△COE≌△OAB,则有OE=AB;利用等腰三角形性质证明DE=OE,因此CD-AB=CD-DE=CE=R.
详解:连接OA、OB,则△OAB为等腰三角形,顶角为36°,底角为72°;
连接OC、OD,则△OCD为等腰三角形,顶角为108°,底角为36°.
在CD上取一点E,使得CE=OC,连接OE,则△OCE为等腰三角形,顶角为36°,底角为72°.在△COE与△OAB中,CO=AO=R,∠OCE=∠AOB=36°,CE=OB=R,
∴△COE≌△OAB(SAS), ∴OE=AB. ∵∠EOD=∠OEC-∠ODC=72°-36°=36°,
∴∠EOD=∠ODE, ∴DE=OE, ∴CD-AB=CD-OE=CD-DE=CE=R. 故选A.
点睛:此题考查了圆心角、弧、弦的关系、全等三角形、等腰三角形等知识,解题关键是添加辅助线,构造等腰三角形.
6.C
【解析】【分析】连接OA,OB,可以利用SAS判定△OAE≌△OBF,根据全等三角形的对应边相等,可得到OE=OF,判断A选项正确;由全等三角形的对应角相等,可得到∠AOE=∠BOF,即∠AOC=∠BOD,根据圆心角、弧、弦的关系定理得出,判断B选项正确;连结AD,由,根据圆周角定理得出∠BAD=∠ADC,则CD∥AB,判断D选项正确;由∠BOD=∠AOC不一定等于∠COD,得出不一定等于那么AC=BD不一定等于CD,判断C选项不正确.
【详解】连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.
在△OAE与△OBF中,,
∴△OAE≌△OBF(SAS),
∴OE=OF,故A选项正确;
∠AOE=∠BOF,即∠AOC=∠BOD,
∴,故B选项正确;
连结AD,
∵,
∴∠BAD=∠ADC,
∴CD∥AB,故D选项正确;
∵∠BOD=∠AOC不一定等于∠COD,
∴不一定等于,
∴AC=BD不一定等于CD,
故C选项不正确,
故选C.
【点睛】本题考查了全等三角形的判定与性质,圆心角、弧、弦的关系定理,圆周角定理,平行线的判定,准确作出辅助线利用数形结合思想是解题的关键.
7.B
【解析】∵,
∴∠BOC=∠DOE=∠COD=38°,
∴∠BOE=∠BOC+∠DOE+∠COD=114°,
∴∠AOE=180°-∠BOE=66°,
∵OA=OE,
∴∠AEO=(180°-∠AOE)÷2=57°,
故选B.
8.A
【解析】连接OE,如图所示:
∵弧DE为40°的弧, ∴∠DOE=40°. ∵OD=OE, ∴∠ODE= =70°. ∵弦DE∥AB, ∴∠AOC=∠ODE=70°, ∴∠BOC=180°-∠AOC=180°-70°=110°. 故选A.
【点睛】本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.
9.125°
【解析】分析: 连接OD,由∠AOC=40°,可得出∠BOC,再由D是BC弧的中点,可得出∠COD,从而得出∠ACD即可.
详解: 连接OD,
∵AB是⊙O的直径,∠AOC=40°,
∴∠BOC=140°,∠ACO=(180°-40°)÷2=70°,
∵D是BC弧的中点,
∴∠COD=70°,
∴∠OCD=(180°-70°)÷2=55°,
∴∠ACD=∠ACO+∠OCD=70°+55°=125°,
故答案为:125°.
点睛: 本题考查了圆心角、弧、弦的关系,等腰三角形的性质.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
10.144
【解析】【分析】根据在同圆中等弧对的圆心角相等进行分析即可.
【详解】∵弧AB=弧BC,且弧AB:弧AmC=3:4,
∴弧ABC:弧AmC=6:4,
∴∠AOC的度数为(360°÷10)×4=144°,
故答案为:144.
【点睛】本题考查了圆心角、弧、弦的关系,熟知在同圆中等弧对的圆心角相等,一个周角为360度是解题的关键.
11.75
【解析】∵,∠COD=35°,
∴∠BOC=∠DOE=∠COD=35°,
∴∠AOE=180°-∠BOC-∠COD-∠DOE=75°,
故答案为:75°.
【点睛】本题考查了弧、弦、圆心角的关系,在同圆或等圆中,相等的弧所对的圆心角也相等,熟知相关性质是解题的关键.
12.
【解析】解:∵OA=OB,OC=OD,∴∠OBA=∠A=65°,∠OCD=∠D=60°,
∴∠AOB=180°﹣2×65°=50°,∠COD=180°﹣2×60°=60°,∴∠BOC=∠AOD﹣∠AOB﹣∠COD=150°﹣50°﹣60°=40°,∴弧BC的度数为40°.故答案为:40.
点睛:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.
13.50
【解析】解:连接OA、OD,∵AB=CD,∴ ,∴ ,∴AC=BD,在△APC和△DPB中,∵∠PAC=∠PDB,∠APC=∠DPB,AC=BD,∴△APC≌△DPB,∴PA=PD,在△AOP和△DOP中,∵PA=PD,OA=OD,OP=OP,∴△AOP≌△DOP,∴∠APO=∠DPO=65°,∴∠APD=130°,∴∠APC=50°.故答案为:50.
点睛:本题考查的是圆心角、弧、弦的关系和全等三角形的判定和性质,正确作出辅助线、灵活运用相关的性质和判定定理是解题的关键.
14.30°.
【解析】解:∵=====,
∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG,
∵AB是⊙O的直径,
∴∠AOB=180°,∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG=30°,
∴∠COG=∠COD+∠DOE+∠EOF+∠FOG=120°,
∵OC=OG,∴∠OCG=∠OGC=(180°-120°)=30°.
故答案为30°.
15.
【解析】如图,作点A关于MN的对称点A′,连接A′B交MN于点P,连接AP、OB、OA、OA′,则此时AP+BP的值最小=A′B,
∵∠AMN=30°,A′、A关于MN对称,点B是的中点,
∴∠BON=30°,∠A′ON=∠AON=60°,
∴∠A′OB=30°+60°=90°,
又∵OA′=OB=OM=2,
∴A′B=,即AP+BP的值最小=.
故答案为: .
16.20
【解析】弦AB=弦CD,所以的度数还是20°.
点睛:
圆心角定理: 圆心角的度数等于它所对的弧的度数. (1)等弧对等圆心角 (2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角. (3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧. (4)圆心角的度数和它们对的弧的度数相等.
17.证明见解析
【解析】试题分析:根据三个圆心角相等得到其对顶角相等,然后根据相等的圆心角所对的弧相等,所对的弦也相等即可证得结论.
在☉O中,∵∠1=∠2=∠3,
又∵AB,CD,EF都是☉O的直径,
∴∠FOD=∠AOC=∠BOE.
∴==,
∴AC=EB=DF.
18.相等.
【解析】试题分析: 首先根据到角的两边的距离相等的点在角的平分线上,可证明平分进而得到至此即可得到与的关系.
试题解析:连
平分
∠1=∠2
点睛:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等;
19.的度数为70°, 的度数为20°.
【解析】
【分析】
连接OC,求出∠B度数,根据等腰三角形性质求出∠BOC,根据OA⊥OB可得∠AOC即可.
【详解】
解:连结OC,
在Rt△AOB中,∠A=35°,
∴∠B=55°,又∵OC=OB,
∴∠COB=180°-2∠B=70°,
∴的度数为70°,
∠COD=90°-∠COB=90°-70°=20°,
∴ 的度数为20°.
【点睛】
本题考查了圆心角、弧、弦之间的关系,等腰三角形性质,三角形内角和定理,正确作出辅助线是解题的关键.
20.证明见解析
【解析】分析: 根据弧相等,则对应的弦相等从而证明AB=AC,则△ABC易证是等边三角形,然后根据同圆中弦相等,则对应的圆心角相等即可证得.
详解:
∵=,
∴AB=AC,
∴△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC.
点睛: 本题考查了圆心角、弧、弦的关系以及等边三角形的判定,正确理解圆心角、弧、弦的关系是关键.
21.(1)证明见解析;(2)四边形OFEG是正方形,理由见解析.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由AB=CD判断,再得到,从而判断AC=BD;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到CF=DF,AG=BG,则利用CD=AB得到AG=DF,然后根据正方形的判定方法可判断四边形OFEG是正方形;
【详解】
(1)证明:∵AB=CD,
∴,
∴,即,
∴AC=BD
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
∵AB⊥CD,OF⊥CD,OG⊥AB,
∴四边形OFEG是矩形,DF=CD,AG=AB.
∵AB=CD,
∴DF=AG.
∵OD=OA,
∴OD=OA,
∴△OFD≌△OGA,
∴OF=OG.
∴矩形OFEG是正方形
【点睛】
本题考查了圆的综合题:熟练掌握垂径定理和圆心角、弧、弦的关系;掌握正方形的判定方法.
22.(1)证明见解析;(2)π.
【解析】
【分析】
(1)根据BC是⊙O的直径,AD⊥BC,弧AB=弧AE,推出∠AGB=∠CAD,即可推得FA=FG.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据弧AB=弧AE,求出∠EOC=60°,即可求出弧EC的长度是多少.
【详解】
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵=,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵=,
∴∠AOE=60°.
∴∠EOC=60°.
∴的长为2π×(2+2)×=π.
【点睛】
此题主要考查了圆周角定理和应用,弧、弦、圆心角的关系,弧长的计算方法,等边三角形的判定与性质,要熟练掌握.推出∠AGB=∠CAD是解(1)的关键,推出∠AOB=60°是解答(2)的关键.
3.4 圆心角同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.下列语句中正确的是( )
A. 长度相等的两条弧是等弧 B. 平分弦的直径垂直于弦
C. 相等的圆心角所对的弧相等 D. 经过圆心的每一条直线都是圆的对称轴
2.如图,已知AB是☉O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE=( )
A. 40° B. 60° C. 80° D. 120°
3.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. = B. > C. < D. 不能确定
4.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A. 6 B. 8 C. 5 D. 5
5.如图,在半径为R的⊙O中,和度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).
A. R B. C. 2R D. 3R
6.如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )
A. OE=OF B. 弧AC=弧BD C. AC=CD=DB D. CD∥AB
7.如图,AB是⊙O的直径, ,∠COD=38°,则∠AEO的度数是( )
A. 52° B. 57° C. 66° D. 78°
8.如图,AB和CD是⊙O的两条直径,弦DE∥AB,若∠DOE=40°的弧,则∠BOC=( )
A. 110° B. 80° C. 40° D. 70°
二、填空题
9.如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是BC弧的中点,则∠ACD=?________.
?
10.如图,⊙O中,已知弧AB=弧BC,且弧AB:弧AmC=3:4,则∠AOC=________度.
11.如图,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=35°,则∠AOE=________?°.
12.如图,⊙经过五边形的四个顶点,若, , ,则的度数为__________.
13.如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC的度数为______°.
14.如图,已知AB是⊙O的直径,C、D、E、F、G是上的点,且有,则∠OCG=___.
15.如图,MN是⊙O的直径,OM=2,点A在⊙O上, ,B为弧AN的中点, P是直径MN上一动点,则PA+PB的最小值为 ______________.
16.如图,圆心角∠AOB=20°,将 旋转n°得到,则的度数是______度.
三、解答题
17.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
18.D、E是圆O的半径OA、OB上的点,CD⊥OA、CE⊥OB,CD=CE,则 弧CA与 弧CB?的关系是?
19.如图,已知:在⊙O中,OA⊥OB,∠A=35°,求弧CD和弧BC的度数.
20.如图,在⊙O中,=,∠ACB=60°.求证:∠AOB=∠BOC=∠AOC.
21.如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
22.如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
参考答案
1.D
【解析】分析:根据垂径定理及逆定理以及圆的性质来进行判定分析即可得出答案.
详解:A、在同圆或等圆中,长度相等的两条弧是等弧;B、平分弦(不是直径)的直径垂直于弦;C、在同圆或等圆中,相等的圆心角所对的弧相等;D、经过圆心的每一条直线都是圆的对称轴;故选D.
点睛:本题主要考查的是圆的一些基本性质,属于基础题型.理解圆的性质是解决这个问题的关键.
2.B
【解析】
【分析】
根据等弧所对的圆心角相等求得∠EOD=∠COD=∠BOC,从而可求得∠AOE的度数.
【详解】
∵D、C是劣弧EB的三等分点,∠BOC=40°?,
∴∠EOD=∠COD=∠BOC=40°?,
∴∠AOE=60°.?
故选B.
【点睛】
本题考查了同弧所对的圆心角相等.由D,C是劣弧EB的三等分点求得∠EOD=∠COD=∠BOC是解答本题的关键.
3.D
【解析】分析:根据在同圆和等圆中相等的弦所对的弧相等分析,从而得到答案.
详解:在同圆和等圆中相等的弦所对的弧才会相等,要注意同圆和等圆的条件,本题是两个不同的圆,所以无法判断两弦所对的弧的大小,
故选D.
点睛:本题考查了在同圆和等圆中相等的弦所对的弧相等的理解及运用,解题的关键是不要忽视在同圆或等圆中这一前提条件.
4.B
【解析】【分析】延长AO交⊙O于点E,连接BE,由∠AOB+∠BOE=∠AOB+∠COD知∠BOE=∠COD,据此可得BE=CD=6,在Rt△ABE中利用勾股定理求解可得.
【详解】如图,延长AO交⊙O于点E,连接BE,
则∠AOB+∠BOE=180°,
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6,
∵AE为⊙O的直径,
∴∠ABE=90°,
∴AB==8,
故选B.
【点睛】本题考查了弧、弦、圆心角的关系,圆周角定理等,正确添加辅助线以及熟练应用相关的性质与定理是解题的关键.
5.A
【解析】分析:如解答图,作辅助线,构造三个等腰三角形△OAB,△OCD与△OCE;证明△COE≌△OAB,则有OE=AB;利用等腰三角形性质证明DE=OE,因此CD-AB=CD-DE=CE=R.
详解:连接OA、OB,则△OAB为等腰三角形,顶角为36°,底角为72°;
连接OC、OD,则△OCD为等腰三角形,顶角为108°,底角为36°.
在CD上取一点E,使得CE=OC,连接OE,则△OCE为等腰三角形,顶角为36°,底角为72°.在△COE与△OAB中,CO=AO=R,∠OCE=∠AOB=36°,CE=OB=R,
∴△COE≌△OAB(SAS), ∴OE=AB. ∵∠EOD=∠OEC-∠ODC=72°-36°=36°,
∴∠EOD=∠ODE, ∴DE=OE, ∴CD-AB=CD-OE=CD-DE=CE=R. 故选A.
点睛:此题考查了圆心角、弧、弦的关系、全等三角形、等腰三角形等知识,解题关键是添加辅助线,构造等腰三角形.
6.C
【解析】【分析】连接OA,OB,可以利用SAS判定△OAE≌△OBF,根据全等三角形的对应边相等,可得到OE=OF,判断A选项正确;由全等三角形的对应角相等,可得到∠AOE=∠BOF,即∠AOC=∠BOD,根据圆心角、弧、弦的关系定理得出,判断B选项正确;连结AD,由,根据圆周角定理得出∠BAD=∠ADC,则CD∥AB,判断D选项正确;由∠BOD=∠AOC不一定等于∠COD,得出不一定等于那么AC=BD不一定等于CD,判断C选项不正确.
【详解】连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.
在△OAE与△OBF中,,
∴△OAE≌△OBF(SAS),
∴OE=OF,故A选项正确;
∠AOE=∠BOF,即∠AOC=∠BOD,
∴,故B选项正确;
连结AD,
∵,
∴∠BAD=∠ADC,
∴CD∥AB,故D选项正确;
∵∠BOD=∠AOC不一定等于∠COD,
∴不一定等于,
∴AC=BD不一定等于CD,
故C选项不正确,
故选C.
【点睛】本题考查了全等三角形的判定与性质,圆心角、弧、弦的关系定理,圆周角定理,平行线的判定,准确作出辅助线利用数形结合思想是解题的关键.
7.B
【解析】∵,
∴∠BOC=∠DOE=∠COD=38°,
∴∠BOE=∠BOC+∠DOE+∠COD=114°,
∴∠AOE=180°-∠BOE=66°,
∵OA=OE,
∴∠AEO=(180°-∠AOE)÷2=57°,
故选B.
8.A
【解析】连接OE,如图所示:
∵弧DE为40°的弧, ∴∠DOE=40°. ∵OD=OE, ∴∠ODE= =70°. ∵弦DE∥AB, ∴∠AOC=∠ODE=70°, ∴∠BOC=180°-∠AOC=180°-70°=110°. 故选A.
【点睛】本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.
9.125°
【解析】分析: 连接OD,由∠AOC=40°,可得出∠BOC,再由D是BC弧的中点,可得出∠COD,从而得出∠ACD即可.
详解: 连接OD,
∵AB是⊙O的直径,∠AOC=40°,
∴∠BOC=140°,∠ACO=(180°-40°)÷2=70°,
∵D是BC弧的中点,
∴∠COD=70°,
∴∠OCD=(180°-70°)÷2=55°,
∴∠ACD=∠ACO+∠OCD=70°+55°=125°,
故答案为:125°.
点睛: 本题考查了圆心角、弧、弦的关系,等腰三角形的性质.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
10.144
【解析】【分析】根据在同圆中等弧对的圆心角相等进行分析即可.
【详解】∵弧AB=弧BC,且弧AB:弧AmC=3:4,
∴弧ABC:弧AmC=6:4,
∴∠AOC的度数为(360°÷10)×4=144°,
故答案为:144.
【点睛】本题考查了圆心角、弧、弦的关系,熟知在同圆中等弧对的圆心角相等,一个周角为360度是解题的关键.
11.75
【解析】∵,∠COD=35°,
∴∠BOC=∠DOE=∠COD=35°,
∴∠AOE=180°-∠BOC-∠COD-∠DOE=75°,
故答案为:75°.
【点睛】本题考查了弧、弦、圆心角的关系,在同圆或等圆中,相等的弧所对的圆心角也相等,熟知相关性质是解题的关键.
12.
【解析】解:∵OA=OB,OC=OD,∴∠OBA=∠A=65°,∠OCD=∠D=60°,
∴∠AOB=180°﹣2×65°=50°,∠COD=180°﹣2×60°=60°,∴∠BOC=∠AOD﹣∠AOB﹣∠COD=150°﹣50°﹣60°=40°,∴弧BC的度数为40°.故答案为:40.
点睛:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.
13.50
【解析】解:连接OA、OD,∵AB=CD,∴ ,∴ ,∴AC=BD,在△APC和△DPB中,∵∠PAC=∠PDB,∠APC=∠DPB,AC=BD,∴△APC≌△DPB,∴PA=PD,在△AOP和△DOP中,∵PA=PD,OA=OD,OP=OP,∴△AOP≌△DOP,∴∠APO=∠DPO=65°,∴∠APD=130°,∴∠APC=50°.故答案为:50.
点睛:本题考查的是圆心角、弧、弦的关系和全等三角形的判定和性质,正确作出辅助线、灵活运用相关的性质和判定定理是解题的关键.
14.30°.
【解析】解:∵=====,
∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG,
∵AB是⊙O的直径,
∴∠AOB=180°,∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG=30°,
∴∠COG=∠COD+∠DOE+∠EOF+∠FOG=120°,
∵OC=OG,∴∠OCG=∠OGC=(180°-120°)=30°.
故答案为30°.
15.
【解析】如图,作点A关于MN的对称点A′,连接A′B交MN于点P,连接AP、OB、OA、OA′,则此时AP+BP的值最小=A′B,
∵∠AMN=30°,A′、A关于MN对称,点B是的中点,
∴∠BON=30°,∠A′ON=∠AON=60°,
∴∠A′OB=30°+60°=90°,
又∵OA′=OB=OM=2,
∴A′B=,即AP+BP的值最小=.
故答案为: .
16.20
【解析】弦AB=弦CD,所以的度数还是20°.
点睛:
圆心角定理: 圆心角的度数等于它所对的弧的度数. (1)等弧对等圆心角 (2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角. (3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧. (4)圆心角的度数和它们对的弧的度数相等.
17.证明见解析
【解析】试题分析:根据三个圆心角相等得到其对顶角相等,然后根据相等的圆心角所对的弧相等,所对的弦也相等即可证得结论.
在☉O中,∵∠1=∠2=∠3,
又∵AB,CD,EF都是☉O的直径,
∴∠FOD=∠AOC=∠BOE.
∴==,
∴AC=EB=DF.
18.相等.
【解析】试题分析: 首先根据到角的两边的距离相等的点在角的平分线上,可证明平分进而得到至此即可得到与的关系.
试题解析:连
平分
∠1=∠2
点睛:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等;
19.的度数为70°, 的度数为20°.
【解析】
【分析】
连接OC,求出∠B度数,根据等腰三角形性质求出∠BOC,根据OA⊥OB可得∠AOC即可.
【详解】
解:连结OC,
在Rt△AOB中,∠A=35°,
∴∠B=55°,又∵OC=OB,
∴∠COB=180°-2∠B=70°,
∴的度数为70°,
∠COD=90°-∠COB=90°-70°=20°,
∴ 的度数为20°.
【点睛】
本题考查了圆心角、弧、弦之间的关系,等腰三角形性质,三角形内角和定理,正确作出辅助线是解题的关键.
20.证明见解析
【解析】分析: 根据弧相等,则对应的弦相等从而证明AB=AC,则△ABC易证是等边三角形,然后根据同圆中弦相等,则对应的圆心角相等即可证得.
详解:
∵=,
∴AB=AC,
∴△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC.
点睛: 本题考查了圆心角、弧、弦的关系以及等边三角形的判定,正确理解圆心角、弧、弦的关系是关键.
21.(1)证明见解析;(2)四边形OFEG是正方形,理由见解析.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由AB=CD判断,再得到,从而判断AC=BD;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到CF=DF,AG=BG,则利用CD=AB得到AG=DF,然后根据正方形的判定方法可判断四边形OFEG是正方形;
【详解】
(1)证明:∵AB=CD,
∴,
∴,即,
∴AC=BD
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
∵AB⊥CD,OF⊥CD,OG⊥AB,
∴四边形OFEG是矩形,DF=CD,AG=AB.
∵AB=CD,
∴DF=AG.
∵OD=OA,
∴OD=OA,
∴△OFD≌△OGA,
∴OF=OG.
∴矩形OFEG是正方形
【点睛】
本题考查了圆的综合题:熟练掌握垂径定理和圆心角、弧、弦的关系;掌握正方形的判定方法.
22.(1)证明见解析;(2)π.
【解析】
【分析】
(1)根据BC是⊙O的直径,AD⊥BC,弧AB=弧AE,推出∠AGB=∠CAD,即可推得FA=FG.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据弧AB=弧AE,求出∠EOC=60°,即可求出弧EC的长度是多少.
【详解】
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵=,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵=,
∴∠AOE=60°.
∴∠EOC=60°.
∴的长为2π×(2+2)×=π.
【点睛】
此题主要考查了圆周角定理和应用,弧、弦、圆心角的关系,弧长的计算方法,等边三角形的判定与性质,要熟练掌握.推出∠AGB=∠CAD是解(1)的关键,推出∠AOB=60°是解答(2)的关键.
姓名:___________班级:___________考号:___________
一、选择题
1.下列语句中正确的是( )
A. 长度相等的两条弧是等弧 B. 平分弦的直径垂直于弦
C. 相等的圆心角所对的弧相等 D. 经过圆心的每一条直线都是圆的对称轴
2.如图,已知AB是☉O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE=( )
A. 40° B. 60° C. 80° D. 120°
3.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. = B. > C. < D. 不能确定
4.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A. 6 B. 8 C. 5 D. 5
5.如图,在半径为R的⊙O中,和度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).
A. R B. C. 2R D. 3R
6.如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )
A. OE=OF B. 弧AC=弧BD C. AC=CD=DB D. CD∥AB
7.如图,AB是⊙O的直径, ,∠COD=38°,则∠AEO的度数是( )
A. 52° B. 57° C. 66° D. 78°
8.如图,AB和CD是⊙O的两条直径,弦DE∥AB,若∠DOE=40°的弧,则∠BOC=( )
A. 110° B. 80° C. 40° D. 70°
二、填空题
9.如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是BC弧的中点,则∠ACD=?________.
?
10.如图,⊙O中,已知弧AB=弧BC,且弧AB:弧AmC=3:4,则∠AOC=________度.
11.如图,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=35°,则∠AOE=________?°.
12.如图,⊙经过五边形的四个顶点,若, , ,则的度数为__________.
13.如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC的度数为______°.
14.如图,已知AB是⊙O的直径,C、D、E、F、G是上的点,且有,则∠OCG=___.
15.如图,MN是⊙O的直径,OM=2,点A在⊙O上, ,B为弧AN的中点, P是直径MN上一动点,则PA+PB的最小值为 ______________.
16.如图,圆心角∠AOB=20°,将 旋转n°得到,则的度数是______度.
三、解答题
17.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
18.D、E是圆O的半径OA、OB上的点,CD⊥OA、CE⊥OB,CD=CE,则 弧CA与 弧CB?的关系是?
19.如图,已知:在⊙O中,OA⊥OB,∠A=35°,求弧CD和弧BC的度数.
20.如图,在⊙O中,=,∠ACB=60°.求证:∠AOB=∠BOC=∠AOC.
21.如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
22.如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
参考答案
1.D
【解析】分析:根据垂径定理及逆定理以及圆的性质来进行判定分析即可得出答案.
详解:A、在同圆或等圆中,长度相等的两条弧是等弧;B、平分弦(不是直径)的直径垂直于弦;C、在同圆或等圆中,相等的圆心角所对的弧相等;D、经过圆心的每一条直线都是圆的对称轴;故选D.
点睛:本题主要考查的是圆的一些基本性质,属于基础题型.理解圆的性质是解决这个问题的关键.
2.B
【解析】
【分析】
根据等弧所对的圆心角相等求得∠EOD=∠COD=∠BOC,从而可求得∠AOE的度数.
【详解】
∵D、C是劣弧EB的三等分点,∠BOC=40°?,
∴∠EOD=∠COD=∠BOC=40°?,
∴∠AOE=60°.?
故选B.
【点睛】
本题考查了同弧所对的圆心角相等.由D,C是劣弧EB的三等分点求得∠EOD=∠COD=∠BOC是解答本题的关键.
3.D
【解析】分析:根据在同圆和等圆中相等的弦所对的弧相等分析,从而得到答案.
详解:在同圆和等圆中相等的弦所对的弧才会相等,要注意同圆和等圆的条件,本题是两个不同的圆,所以无法判断两弦所对的弧的大小,
故选D.
点睛:本题考查了在同圆和等圆中相等的弦所对的弧相等的理解及运用,解题的关键是不要忽视在同圆或等圆中这一前提条件.
4.B
【解析】【分析】延长AO交⊙O于点E,连接BE,由∠AOB+∠BOE=∠AOB+∠COD知∠BOE=∠COD,据此可得BE=CD=6,在Rt△ABE中利用勾股定理求解可得.
【详解】如图,延长AO交⊙O于点E,连接BE,
则∠AOB+∠BOE=180°,
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6,
∵AE为⊙O的直径,
∴∠ABE=90°,
∴AB==8,
故选B.
【点睛】本题考查了弧、弦、圆心角的关系,圆周角定理等,正确添加辅助线以及熟练应用相关的性质与定理是解题的关键.
5.A
【解析】分析:如解答图,作辅助线,构造三个等腰三角形△OAB,△OCD与△OCE;证明△COE≌△OAB,则有OE=AB;利用等腰三角形性质证明DE=OE,因此CD-AB=CD-DE=CE=R.
详解:连接OA、OB,则△OAB为等腰三角形,顶角为36°,底角为72°;
连接OC、OD,则△OCD为等腰三角形,顶角为108°,底角为36°.
在CD上取一点E,使得CE=OC,连接OE,则△OCE为等腰三角形,顶角为36°,底角为72°.在△COE与△OAB中,CO=AO=R,∠OCE=∠AOB=36°,CE=OB=R,
∴△COE≌△OAB(SAS), ∴OE=AB. ∵∠EOD=∠OEC-∠ODC=72°-36°=36°,
∴∠EOD=∠ODE, ∴DE=OE, ∴CD-AB=CD-OE=CD-DE=CE=R. 故选A.
点睛:此题考查了圆心角、弧、弦的关系、全等三角形、等腰三角形等知识,解题关键是添加辅助线,构造等腰三角形.
6.C
【解析】【分析】连接OA,OB,可以利用SAS判定△OAE≌△OBF,根据全等三角形的对应边相等,可得到OE=OF,判断A选项正确;由全等三角形的对应角相等,可得到∠AOE=∠BOF,即∠AOC=∠BOD,根据圆心角、弧、弦的关系定理得出,判断B选项正确;连结AD,由,根据圆周角定理得出∠BAD=∠ADC,则CD∥AB,判断D选项正确;由∠BOD=∠AOC不一定等于∠COD,得出不一定等于那么AC=BD不一定等于CD,判断C选项不正确.
【详解】连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.
在△OAE与△OBF中,,
∴△OAE≌△OBF(SAS),
∴OE=OF,故A选项正确;
∠AOE=∠BOF,即∠AOC=∠BOD,
∴,故B选项正确;
连结AD,
∵,
∴∠BAD=∠ADC,
∴CD∥AB,故D选项正确;
∵∠BOD=∠AOC不一定等于∠COD,
∴不一定等于,
∴AC=BD不一定等于CD,
故C选项不正确,
故选C.
【点睛】本题考查了全等三角形的判定与性质,圆心角、弧、弦的关系定理,圆周角定理,平行线的判定,准确作出辅助线利用数形结合思想是解题的关键.
7.B
【解析】∵,
∴∠BOC=∠DOE=∠COD=38°,
∴∠BOE=∠BOC+∠DOE+∠COD=114°,
∴∠AOE=180°-∠BOE=66°,
∵OA=OE,
∴∠AEO=(180°-∠AOE)÷2=57°,
故选B.
8.A
【解析】连接OE,如图所示:
∵弧DE为40°的弧, ∴∠DOE=40°. ∵OD=OE, ∴∠ODE= =70°. ∵弦DE∥AB, ∴∠AOC=∠ODE=70°, ∴∠BOC=180°-∠AOC=180°-70°=110°. 故选A.
【点睛】本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.
9.125°
【解析】分析: 连接OD,由∠AOC=40°,可得出∠BOC,再由D是BC弧的中点,可得出∠COD,从而得出∠ACD即可.
详解: 连接OD,
∵AB是⊙O的直径,∠AOC=40°,
∴∠BOC=140°,∠ACO=(180°-40°)÷2=70°,
∵D是BC弧的中点,
∴∠COD=70°,
∴∠OCD=(180°-70°)÷2=55°,
∴∠ACD=∠ACO+∠OCD=70°+55°=125°,
故答案为:125°.
点睛: 本题考查了圆心角、弧、弦的关系,等腰三角形的性质.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
10.144
【解析】【分析】根据在同圆中等弧对的圆心角相等进行分析即可.
【详解】∵弧AB=弧BC,且弧AB:弧AmC=3:4,
∴弧ABC:弧AmC=6:4,
∴∠AOC的度数为(360°÷10)×4=144°,
故答案为:144.
【点睛】本题考查了圆心角、弧、弦的关系,熟知在同圆中等弧对的圆心角相等,一个周角为360度是解题的关键.
11.75
【解析】∵,∠COD=35°,
∴∠BOC=∠DOE=∠COD=35°,
∴∠AOE=180°-∠BOC-∠COD-∠DOE=75°,
故答案为:75°.
【点睛】本题考查了弧、弦、圆心角的关系,在同圆或等圆中,相等的弧所对的圆心角也相等,熟知相关性质是解题的关键.
12.
【解析】解:∵OA=OB,OC=OD,∴∠OBA=∠A=65°,∠OCD=∠D=60°,
∴∠AOB=180°﹣2×65°=50°,∠COD=180°﹣2×60°=60°,∴∠BOC=∠AOD﹣∠AOB﹣∠COD=150°﹣50°﹣60°=40°,∴弧BC的度数为40°.故答案为:40.
点睛:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.
13.50
【解析】解:连接OA、OD,∵AB=CD,∴ ,∴ ,∴AC=BD,在△APC和△DPB中,∵∠PAC=∠PDB,∠APC=∠DPB,AC=BD,∴△APC≌△DPB,∴PA=PD,在△AOP和△DOP中,∵PA=PD,OA=OD,OP=OP,∴△AOP≌△DOP,∴∠APO=∠DPO=65°,∴∠APD=130°,∴∠APC=50°.故答案为:50.
点睛:本题考查的是圆心角、弧、弦的关系和全等三角形的判定和性质,正确作出辅助线、灵活运用相关的性质和判定定理是解题的关键.
14.30°.
【解析】解:∵=====,
∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG,
∵AB是⊙O的直径,
∴∠AOB=180°,∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG=30°,
∴∠COG=∠COD+∠DOE+∠EOF+∠FOG=120°,
∵OC=OG,∴∠OCG=∠OGC=(180°-120°)=30°.
故答案为30°.
15.
【解析】如图,作点A关于MN的对称点A′,连接A′B交MN于点P,连接AP、OB、OA、OA′,则此时AP+BP的值最小=A′B,
∵∠AMN=30°,A′、A关于MN对称,点B是的中点,
∴∠BON=30°,∠A′ON=∠AON=60°,
∴∠A′OB=30°+60°=90°,
又∵OA′=OB=OM=2,
∴A′B=,即AP+BP的值最小=.
故答案为: .
16.20
【解析】弦AB=弦CD,所以的度数还是20°.
点睛:
圆心角定理: 圆心角的度数等于它所对的弧的度数. (1)等弧对等圆心角 (2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角. (3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧. (4)圆心角的度数和它们对的弧的度数相等.
17.证明见解析
【解析】试题分析:根据三个圆心角相等得到其对顶角相等,然后根据相等的圆心角所对的弧相等,所对的弦也相等即可证得结论.
在☉O中,∵∠1=∠2=∠3,
又∵AB,CD,EF都是☉O的直径,
∴∠FOD=∠AOC=∠BOE.
∴==,
∴AC=EB=DF.
18.相等.
【解析】试题分析: 首先根据到角的两边的距离相等的点在角的平分线上,可证明平分进而得到至此即可得到与的关系.
试题解析:连
平分
∠1=∠2
点睛:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等;
19.的度数为70°, 的度数为20°.
【解析】
【分析】
连接OC,求出∠B度数,根据等腰三角形性质求出∠BOC,根据OA⊥OB可得∠AOC即可.
【详解】
解:连结OC,
在Rt△AOB中,∠A=35°,
∴∠B=55°,又∵OC=OB,
∴∠COB=180°-2∠B=70°,
∴的度数为70°,
∠COD=90°-∠COB=90°-70°=20°,
∴ 的度数为20°.
【点睛】
本题考查了圆心角、弧、弦之间的关系,等腰三角形性质,三角形内角和定理,正确作出辅助线是解题的关键.
20.证明见解析
【解析】分析: 根据弧相等,则对应的弦相等从而证明AB=AC,则△ABC易证是等边三角形,然后根据同圆中弦相等,则对应的圆心角相等即可证得.
详解:
∵=,
∴AB=AC,
∴△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC.
点睛: 本题考查了圆心角、弧、弦的关系以及等边三角形的判定,正确理解圆心角、弧、弦的关系是关键.
21.(1)证明见解析;(2)四边形OFEG是正方形,理由见解析.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由AB=CD判断,再得到,从而判断AC=BD;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到CF=DF,AG=BG,则利用CD=AB得到AG=DF,然后根据正方形的判定方法可判断四边形OFEG是正方形;
【详解】
(1)证明:∵AB=CD,
∴,
∴,即,
∴AC=BD
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
∵AB⊥CD,OF⊥CD,OG⊥AB,
∴四边形OFEG是矩形,DF=CD,AG=AB.
∵AB=CD,
∴DF=AG.
∵OD=OA,
∴OD=OA,
∴△OFD≌△OGA,
∴OF=OG.
∴矩形OFEG是正方形
【点睛】
本题考查了圆的综合题:熟练掌握垂径定理和圆心角、弧、弦的关系;掌握正方形的判定方法.
22.(1)证明见解析;(2)π.
【解析】
【分析】
(1)根据BC是⊙O的直径,AD⊥BC,弧AB=弧AE,推出∠AGB=∠CAD,即可推得FA=FG.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据弧AB=弧AE,求出∠EOC=60°,即可求出弧EC的长度是多少.
【详解】
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵=,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵=,
∴∠AOE=60°.
∴∠EOC=60°.
∴的长为2π×(2+2)×=π.
【点睛】
此题主要考查了圆周角定理和应用,弧、弦、圆心角的关系,弧长的计算方法,等边三角形的判定与性质,要熟练掌握.推出∠AGB=∠CAD是解(1)的关键,推出∠AOB=60°是解答(2)的关键.
3.4 圆心角同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.下列语句中正确的是( )
A. 长度相等的两条弧是等弧 B. 平分弦的直径垂直于弦
C. 相等的圆心角所对的弧相等 D. 经过圆心的每一条直线都是圆的对称轴
2.如图,已知AB是☉O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE=( )
A. 40° B. 60° C. 80° D. 120°
3.已知AB、CD是两个不同圆的弦,如AB=CD,那么与的关系是( )
A. = B. > C. < D. 不能确定
4.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A. 6 B. 8 C. 5 D. 5
5.如图,在半径为R的⊙O中,和度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).
A. R B. C. 2R D. 3R
6.如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )
A. OE=OF B. 弧AC=弧BD C. AC=CD=DB D. CD∥AB
7.如图,AB是⊙O的直径, ,∠COD=38°,则∠AEO的度数是( )
A. 52° B. 57° C. 66° D. 78°
8.如图,AB和CD是⊙O的两条直径,弦DE∥AB,若∠DOE=40°的弧,则∠BOC=( )
A. 110° B. 80° C. 40° D. 70°
二、填空题
9.如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是BC弧的中点,则∠ACD=?________.
?
10.如图,⊙O中,已知弧AB=弧BC,且弧AB:弧AmC=3:4,则∠AOC=________度.
11.如图,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=35°,则∠AOE=________?°.
12.如图,⊙经过五边形的四个顶点,若, , ,则的度数为__________.
13.如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC的度数为______°.
14.如图,已知AB是⊙O的直径,C、D、E、F、G是上的点,且有,则∠OCG=___.
15.如图,MN是⊙O的直径,OM=2,点A在⊙O上, ,B为弧AN的中点, P是直径MN上一动点,则PA+PB的最小值为 ______________.
16.如图,圆心角∠AOB=20°,将 旋转n°得到,则的度数是______度.
三、解答题
17.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
18.D、E是圆O的半径OA、OB上的点,CD⊥OA、CE⊥OB,CD=CE,则 弧CA与 弧CB?的关系是?
19.如图,已知:在⊙O中,OA⊥OB,∠A=35°,求弧CD和弧BC的度数.
20.如图,在⊙O中,=,∠ACB=60°.求证:∠AOB=∠BOC=∠AOC.
21.如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
22.如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
参考答案
1.D
【解析】分析:根据垂径定理及逆定理以及圆的性质来进行判定分析即可得出答案.
详解:A、在同圆或等圆中,长度相等的两条弧是等弧;B、平分弦(不是直径)的直径垂直于弦;C、在同圆或等圆中,相等的圆心角所对的弧相等;D、经过圆心的每一条直线都是圆的对称轴;故选D.
点睛:本题主要考查的是圆的一些基本性质,属于基础题型.理解圆的性质是解决这个问题的关键.
2.B
【解析】
【分析】
根据等弧所对的圆心角相等求得∠EOD=∠COD=∠BOC,从而可求得∠AOE的度数.
【详解】
∵D、C是劣弧EB的三等分点,∠BOC=40°?,
∴∠EOD=∠COD=∠BOC=40°?,
∴∠AOE=60°.?
故选B.
【点睛】
本题考查了同弧所对的圆心角相等.由D,C是劣弧EB的三等分点求得∠EOD=∠COD=∠BOC是解答本题的关键.
3.D
【解析】分析:根据在同圆和等圆中相等的弦所对的弧相等分析,从而得到答案.
详解:在同圆和等圆中相等的弦所对的弧才会相等,要注意同圆和等圆的条件,本题是两个不同的圆,所以无法判断两弦所对的弧的大小,
故选D.
点睛:本题考查了在同圆和等圆中相等的弦所对的弧相等的理解及运用,解题的关键是不要忽视在同圆或等圆中这一前提条件.
4.B
【解析】【分析】延长AO交⊙O于点E,连接BE,由∠AOB+∠BOE=∠AOB+∠COD知∠BOE=∠COD,据此可得BE=CD=6,在Rt△ABE中利用勾股定理求解可得.
【详解】如图,延长AO交⊙O于点E,连接BE,
则∠AOB+∠BOE=180°,
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6,
∵AE为⊙O的直径,
∴∠ABE=90°,
∴AB==8,
故选B.
【点睛】本题考查了弧、弦、圆心角的关系,圆周角定理等,正确添加辅助线以及熟练应用相关的性质与定理是解题的关键.
5.A
【解析】分析:如解答图,作辅助线,构造三个等腰三角形△OAB,△OCD与△OCE;证明△COE≌△OAB,则有OE=AB;利用等腰三角形性质证明DE=OE,因此CD-AB=CD-DE=CE=R.
详解:连接OA、OB,则△OAB为等腰三角形,顶角为36°,底角为72°;
连接OC、OD,则△OCD为等腰三角形,顶角为108°,底角为36°.
在CD上取一点E,使得CE=OC,连接OE,则△OCE为等腰三角形,顶角为36°,底角为72°.在△COE与△OAB中,CO=AO=R,∠OCE=∠AOB=36°,CE=OB=R,
∴△COE≌△OAB(SAS), ∴OE=AB. ∵∠EOD=∠OEC-∠ODC=72°-36°=36°,
∴∠EOD=∠ODE, ∴DE=OE, ∴CD-AB=CD-OE=CD-DE=CE=R. 故选A.
点睛:此题考查了圆心角、弧、弦的关系、全等三角形、等腰三角形等知识,解题关键是添加辅助线,构造等腰三角形.
6.C
【解析】【分析】连接OA,OB,可以利用SAS判定△OAE≌△OBF,根据全等三角形的对应边相等,可得到OE=OF,判断A选项正确;由全等三角形的对应角相等,可得到∠AOE=∠BOF,即∠AOC=∠BOD,根据圆心角、弧、弦的关系定理得出,判断B选项正确;连结AD,由,根据圆周角定理得出∠BAD=∠ADC,则CD∥AB,判断D选项正确;由∠BOD=∠AOC不一定等于∠COD,得出不一定等于那么AC=BD不一定等于CD,判断C选项不正确.
【详解】连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.
在△OAE与△OBF中,,
∴△OAE≌△OBF(SAS),
∴OE=OF,故A选项正确;
∠AOE=∠BOF,即∠AOC=∠BOD,
∴,故B选项正确;
连结AD,
∵,
∴∠BAD=∠ADC,
∴CD∥AB,故D选项正确;
∵∠BOD=∠AOC不一定等于∠COD,
∴不一定等于,
∴AC=BD不一定等于CD,
故C选项不正确,
故选C.
【点睛】本题考查了全等三角形的判定与性质,圆心角、弧、弦的关系定理,圆周角定理,平行线的判定,准确作出辅助线利用数形结合思想是解题的关键.
7.B
【解析】∵,
∴∠BOC=∠DOE=∠COD=38°,
∴∠BOE=∠BOC+∠DOE+∠COD=114°,
∴∠AOE=180°-∠BOE=66°,
∵OA=OE,
∴∠AEO=(180°-∠AOE)÷2=57°,
故选B.
8.A
【解析】连接OE,如图所示:
∵弧DE为40°的弧, ∴∠DOE=40°. ∵OD=OE, ∴∠ODE= =70°. ∵弦DE∥AB, ∴∠AOC=∠ODE=70°, ∴∠BOC=180°-∠AOC=180°-70°=110°. 故选A.
【点睛】本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.
9.125°
【解析】分析: 连接OD,由∠AOC=40°,可得出∠BOC,再由D是BC弧的中点,可得出∠COD,从而得出∠ACD即可.
详解: 连接OD,
∵AB是⊙O的直径,∠AOC=40°,
∴∠BOC=140°,∠ACO=(180°-40°)÷2=70°,
∵D是BC弧的中点,
∴∠COD=70°,
∴∠OCD=(180°-70°)÷2=55°,
∴∠ACD=∠ACO+∠OCD=70°+55°=125°,
故答案为:125°.
点睛: 本题考查了圆心角、弧、弦的关系,等腰三角形的性质.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
10.144
【解析】【分析】根据在同圆中等弧对的圆心角相等进行分析即可.
【详解】∵弧AB=弧BC,且弧AB:弧AmC=3:4,
∴弧ABC:弧AmC=6:4,
∴∠AOC的度数为(360°÷10)×4=144°,
故答案为:144.
【点睛】本题考查了圆心角、弧、弦的关系,熟知在同圆中等弧对的圆心角相等,一个周角为360度是解题的关键.
11.75
【解析】∵,∠COD=35°,
∴∠BOC=∠DOE=∠COD=35°,
∴∠AOE=180°-∠BOC-∠COD-∠DOE=75°,
故答案为:75°.
【点睛】本题考查了弧、弦、圆心角的关系,在同圆或等圆中,相等的弧所对的圆心角也相等,熟知相关性质是解题的关键.
12.
【解析】解:∵OA=OB,OC=OD,∴∠OBA=∠A=65°,∠OCD=∠D=60°,
∴∠AOB=180°﹣2×65°=50°,∠COD=180°﹣2×60°=60°,∴∠BOC=∠AOD﹣∠AOB﹣∠COD=150°﹣50°﹣60°=40°,∴弧BC的度数为40°.故答案为:40.
点睛:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.
13.50
【解析】解:连接OA、OD,∵AB=CD,∴ ,∴ ,∴AC=BD,在△APC和△DPB中,∵∠PAC=∠PDB,∠APC=∠DPB,AC=BD,∴△APC≌△DPB,∴PA=PD,在△AOP和△DOP中,∵PA=PD,OA=OD,OP=OP,∴△AOP≌△DOP,∴∠APO=∠DPO=65°,∴∠APD=130°,∴∠APC=50°.故答案为:50.
点睛:本题考查的是圆心角、弧、弦的关系和全等三角形的判定和性质,正确作出辅助线、灵活运用相关的性质和判定定理是解题的关键.
14.30°.
【解析】解:∵=====,
∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG,
∵AB是⊙O的直径,
∴∠AOB=180°,∴∠AOC=∠COD=∠DOE=∠EOF=∠FOG=∠BOG=30°,
∴∠COG=∠COD+∠DOE+∠EOF+∠FOG=120°,
∵OC=OG,∴∠OCG=∠OGC=(180°-120°)=30°.
故答案为30°.
15.
【解析】如图,作点A关于MN的对称点A′,连接A′B交MN于点P,连接AP、OB、OA、OA′,则此时AP+BP的值最小=A′B,
∵∠AMN=30°,A′、A关于MN对称,点B是的中点,
∴∠BON=30°,∠A′ON=∠AON=60°,
∴∠A′OB=30°+60°=90°,
又∵OA′=OB=OM=2,
∴A′B=,即AP+BP的值最小=.
故答案为: .
16.20
【解析】弦AB=弦CD,所以的度数还是20°.
点睛:
圆心角定理: 圆心角的度数等于它所对的弧的度数. (1)等弧对等圆心角 (2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角. (3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧. (4)圆心角的度数和它们对的弧的度数相等.
17.证明见解析
【解析】试题分析:根据三个圆心角相等得到其对顶角相等,然后根据相等的圆心角所对的弧相等,所对的弦也相等即可证得结论.
在☉O中,∵∠1=∠2=∠3,
又∵AB,CD,EF都是☉O的直径,
∴∠FOD=∠AOC=∠BOE.
∴==,
∴AC=EB=DF.
18.相等.
【解析】试题分析: 首先根据到角的两边的距离相等的点在角的平分线上,可证明平分进而得到至此即可得到与的关系.
试题解析:连
平分
∠1=∠2
点睛:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等;
19.的度数为70°, 的度数为20°.
【解析】
【分析】
连接OC,求出∠B度数,根据等腰三角形性质求出∠BOC,根据OA⊥OB可得∠AOC即可.
【详解】
解:连结OC,
在Rt△AOB中,∠A=35°,
∴∠B=55°,又∵OC=OB,
∴∠COB=180°-2∠B=70°,
∴的度数为70°,
∠COD=90°-∠COB=90°-70°=20°,
∴ 的度数为20°.
【点睛】
本题考查了圆心角、弧、弦之间的关系,等腰三角形性质,三角形内角和定理,正确作出辅助线是解题的关键.
20.证明见解析
【解析】分析: 根据弧相等,则对应的弦相等从而证明AB=AC,则△ABC易证是等边三角形,然后根据同圆中弦相等,则对应的圆心角相等即可证得.
详解:
∵=,
∴AB=AC,
∴△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC.
点睛: 本题考查了圆心角、弧、弦的关系以及等边三角形的判定,正确理解圆心角、弧、弦的关系是关键.
21.(1)证明见解析;(2)四边形OFEG是正方形,理由见解析.
【解析】
【分析】
(1)根据圆心角、弧、弦的关系先由AB=CD判断,再得到,从而判断AC=BD;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到CF=DF,AG=BG,则利用CD=AB得到AG=DF,然后根据正方形的判定方法可判断四边形OFEG是正方形;
【详解】
(1)证明:∵AB=CD,
∴,
∴,即,
∴AC=BD
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
∵AB⊥CD,OF⊥CD,OG⊥AB,
∴四边形OFEG是矩形,DF=CD,AG=AB.
∵AB=CD,
∴DF=AG.
∵OD=OA,
∴OD=OA,
∴△OFD≌△OGA,
∴OF=OG.
∴矩形OFEG是正方形
【点睛】
本题考查了圆的综合题:熟练掌握垂径定理和圆心角、弧、弦的关系;掌握正方形的判定方法.
22.(1)证明见解析;(2)π.
【解析】
【分析】
(1)根据BC是⊙O的直径,AD⊥BC,弧AB=弧AE,推出∠AGB=∠CAD,即可推得FA=FG.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据弧AB=弧AE,求出∠EOC=60°,即可求出弧EC的长度是多少.
【详解】
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵=,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵=,
∴∠AOE=60°.
∴∠EOC=60°.
∴的长为2π×(2+2)×=π.
【点睛】
此题主要考查了圆周角定理和应用,弧、弦、圆心角的关系,弧长的计算方法,等边三角形的判定与性质,要熟练掌握.推出∠AGB=∠CAD是解(1)的关键,推出∠AOB=60°是解答(2)的关键.
同课章节目录
