3.5 圆周角同步课时作业（2）

3.5 圆周角同步课时作业（2）
姓名：___________班级：___________考号：___________
一、选择题
1．如图，BD是⊙O的直径，∠CBD=30° ，则∠A的度数为（ ）
A． 30° B． 45° C． 60° D． 75°
2．如图，在⊙O中，直径CD⊥弦AB，若∠C=30°，则∠BOD的度数是（　　）
A． 30° B． 40° C． 50° D． 60°
3．如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB=110°，则∠AED的度数为（　　）
A． 15° B． 20° C． 25° D． 30°
4．如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点．下列四个角中，一定与∠ACD互余的角是(　　)
A． ∠ADC B． ∠ABD C． ∠BAC D． ∠BAD
5．如图，OA，OC是⊙O的半径，点B在⊙O上，若AB∥OC，∠BCO=21°，则∠AOC的度数是（　　）
A． 42° B． 21° C． 84° D． 60°
6．如图，AB是⊙O的直径，CD是弦，且AB∥CD，若AB=8，∠ABC=30°，则弦AD的长为（　　）
A． B． C． D． 8
7．如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD，已知DE＝6，∠BAC＋∠EAD＝180°，则弦BC的长等于( )

A． B． C． 8 D． 6
8．如图，A，B，C，D是⊙O上的四个点，B是弧AC的中点，M是半径OD上任意一点．若∠BDC=40°，则∠AMB的度数不可能是（　　）
A． 45° B． 60° C． 75° D． 85°
二、填空题
9．如图，点A，B，C，D分别在⊙O上，，若∠AOB=40°，则∠ADC的大小是_____度．
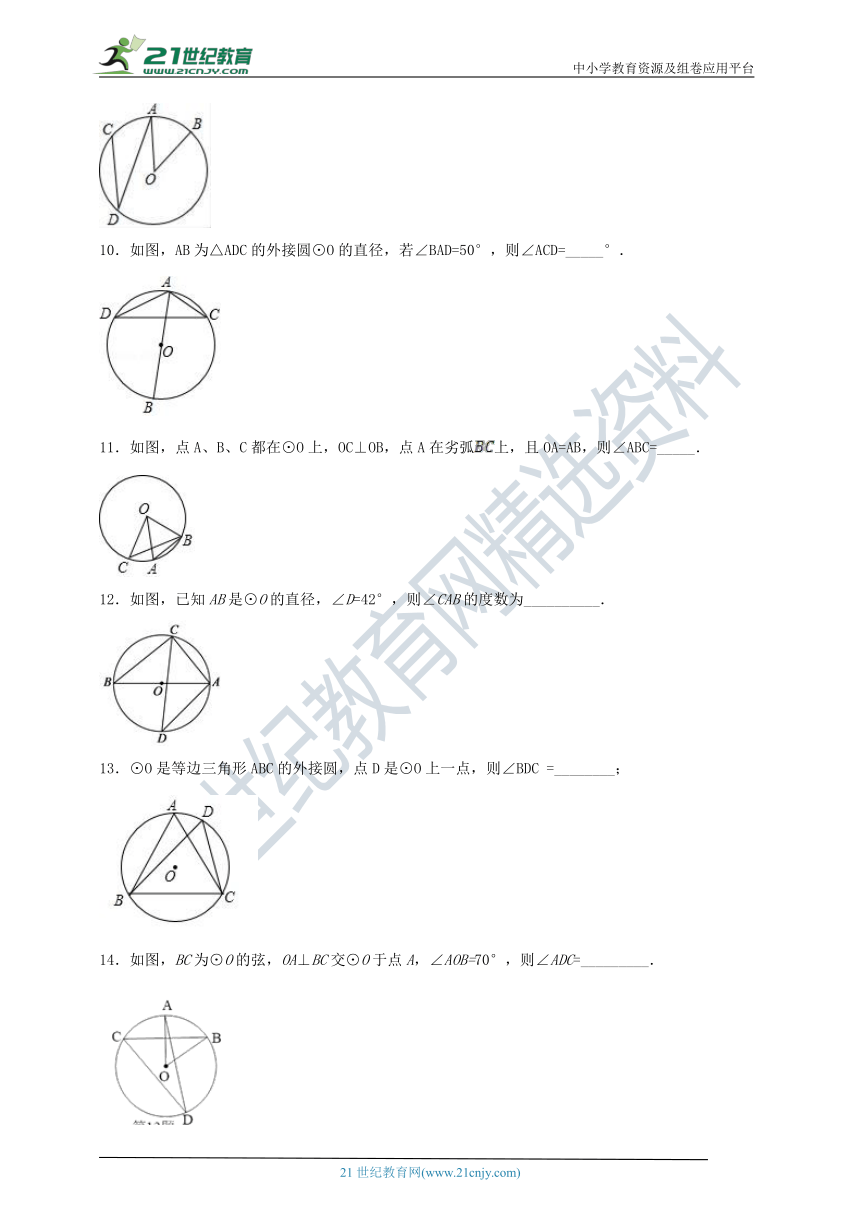
10．如图，AB为△ADC的外接圆⊙O的直径，若∠BAD=50°，则∠ACD=_____°．
11．如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA=AB，则∠ABC=_____．
12．如图，已知AB是⊙O的直径，∠D=42°，则∠CAB的度数为__________．
13．⊙O是等边三角形ABC的外接圆，点D是⊙O上一点，则∠BDC =________；
14．如图，BC为⊙O的弦，OA⊥BC交⊙O于点A，∠AOB=70°，则∠ADC=_________．
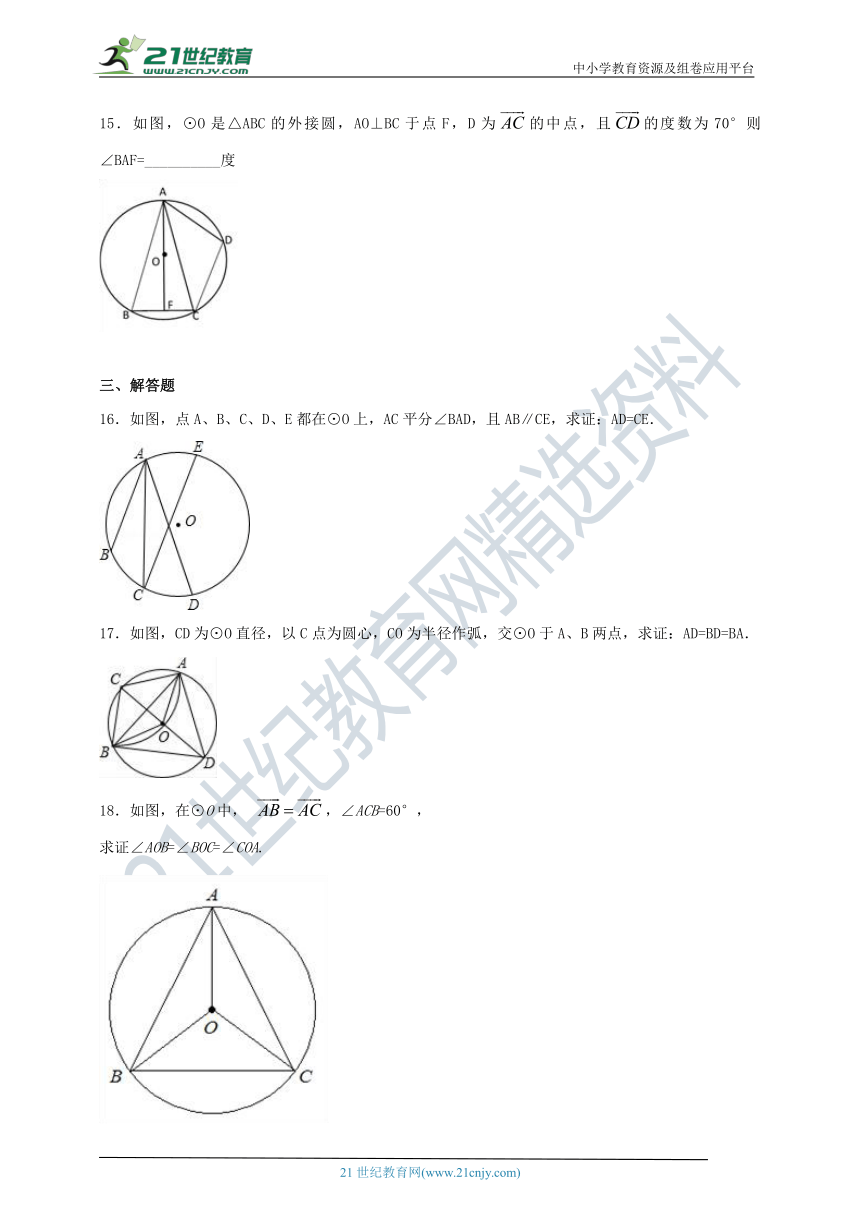
15．如图，⊙O是△ABC的外接圆，AO⊥BC于点F，D为的中点，且的度数为70°则∠BAF=__________度
三、解答题
16．如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：AD=CE．
17．如图，CD为⊙O直径，以C点为圆心，CO为半径作弧，交⊙O于A、B两点，求证：AD=BD=BA．
18．如图，在⊙O中， ，∠ACB=60°，
求证∠AOB=∠BOC=∠COA.
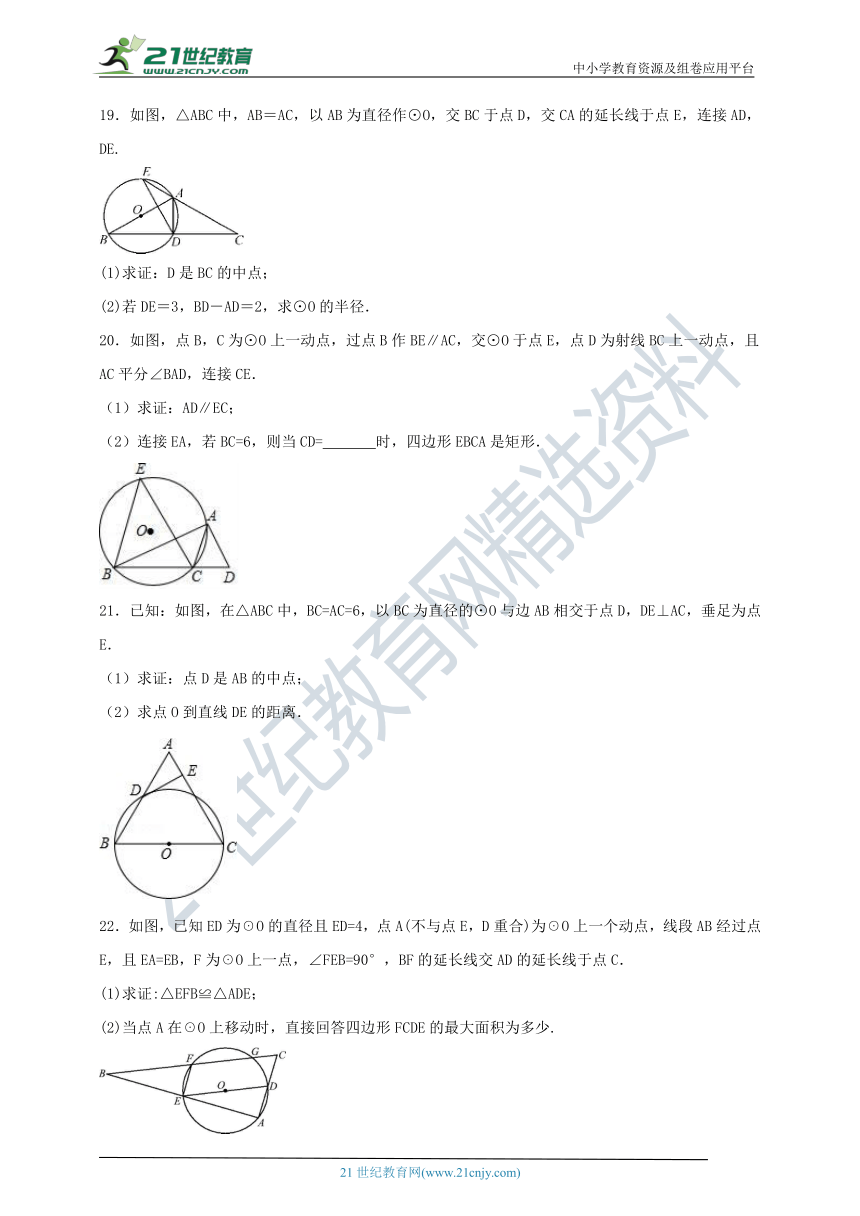
19．如图，△ABC中，AB＝AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD，DE.
(1)求证：D是BC的中点；
(2)若DE＝3，BD－AD＝2，求⊙O的半径．
20．如图，点B，C为⊙O上一动点，过点B作BE∥AC，交⊙O于点E，点D为射线BC上一动点，且AC平分∠BAD，连接CE．
（1）求证：AD∥EC；
（2）连接EA，若BC=6，则当CD=　 　时，四边形EBCA是矩形．
21．已知：如图，在△ABC中，BC=AC=6，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．
（1）求证：点D是AB的中点；
（2）求点O到直线DE的距离．
22．如图，已知ED为☉O的直径且ED=4，点A(不与点E，D重合)为☉O上一个动点，线段AB经过点E，且EA=EB，F为☉O上一点，∠FEB=90°，BF的延长线交AD的延长线于点C．
(1)求证:△EFB≌△ADE；
(2)当点A在☉O上移动时，直接回答四边形FCDE的最大面积为多少.
参考答案
1．C
【解析】
【分析】
先求出∠D的度数，再由圆周角定理即可得出结论．
【详解】
∵BD是⊙O的直径，∴∠BCD=90°．∵∠CBD=30°，∴∠D=90°﹣30°=60°，∴∠A=∠D=60°．
故选C．
【点睛】
本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
2．D
【解析】如图，连接AO，
∵∠C=30°，
∴∠AOD=60°，
∵直径CD⊥弦AB，
∴，
∴∠BOD=∠AOD =60°，
故选D．
3．B
【解析】试题解析：连接AC，如图，
∵AB为直径，
∴∠ACB=90°，
∴
∴
故选B．
点睛：在同圆或等圆中，同弧或等弧所对的圆周角相等.
4．D
【解析】∵∠ACD对的弧是，对的另一个圆周角是∠ABD，
∴∠ABD=∠ACD（同圆中，同弧所对的圆周角相等），
故选B.
5．A
【解析】分析：根据平行线的性质求出∠ABC的度数，然后直接根据圆周角定理即可得出结论．
详解：∵AB∥OC，
∴∠ABC＝∠BCO＝21°，
∵∠ABC与∠AOC是同弧所对的圆周角与圆心角，
∴∠AOC＝2∠ABC＝42°．
故选：A．
点睛：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
6．B
【解析】连接BD，
∵AB∥CD，
∴∠BAD=∠ADC，
∵∠ADC=∠ABC，∠ABC=30°，
∴∠ADC=30°，
∴∠BAD=30°，
∵AB是⊙O的直径，AB=8，
∴∠ADB=90°，∴BD=AB=4，
∴ AD==4，
故选B．
【点睛】本题考查了同弧所对的圆周角相等、直径所对的圆周角是直角等知识，准确识图、添加辅助线是解题的关键.
7．C
【解析】延长CA，交⊙A于点F，
∵∠BAC+∠BAF=180°，∠BAC+∠EAD=180°，∴∠BAF=∠DAE，∴BF=DE=6，∵CF是直径，∴∠ABF=90°，CF=2×5=10，∴BC=.
故选C.
【点睛】运用了圆周角定理、圆心角与弦的关系以及勾股定理．注意准确作出辅助线是解此题的关键．
8．D
【解析】解：∵B是弧AC的中点，∴∠AOB=2∠BDC=80°．又∵M是OD上一点，∴∠AMB≤∠AOB=80°．则不符合条件的只有85°．故选D．
点睛：本题考查了圆周角定理，正确理解圆周角定理求得∠AOB的度数是关键．
9．20
【解析】分析：直接利用圆周角定理求解．
详解：∵=，∴∠ADC=∠AOB=×40°=20°．
故答案为：20．
点睛：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
10．40
【解析】
【分析】
若要利用∠BAD的度数，需构建与其相等的圆周角；连接BD，由圆周角定理可知∠ACD=∠ABD，在Rt△ABD中，求出∠ABD的度数即可得答案．
【详解】
连接BD，如图，
∵AB为△ADC的外接圆⊙O的直径，
∴∠ADB=90°，
∴∠ABD=90°﹣∠BAD=90°﹣50°=40°，
∴∠ACD=∠ABD=40°，
故答案为：40．
【点睛】
本题考查了圆周角定理及其推论：同弧所对的圆周角相等；半圆（弧）和直径所对的圆周角是直角，正确添加辅助线是解题的关键.
11．15°
【解析】分析：根据等边三角形的判定和性质，再利用圆周角定理解答即可．
详解：∵OA=OB，OA=AB，
∴OA=OB=AB，
即△OAB是等边三角形，
∴∠AOB=60°，
∵OC⊥OB，
∴∠COB=90°，
∴∠COA=90°-60°=30°，
∴∠ABC=15°，
故答案为：15°
点睛：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
12．48°
【解析】分析：先根据圆周角定理求出∠B及∠ACB的度数，再由三角形内角和定理即可得出结论．
详解：∵AB是⊙O的直径，∠D=42°，
∴∠B=∠D=42°，∠ACB=90°，
∴∠CAB=90°-42°=48°．
故答案为：48°．
点睛：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等是解答此题的关键．
13．600
【解析】
【分析】
由等边三角形ABC的性质得到∠A=∠ABC=∠ACB=60°，再由圆周角定理即可得到结论．
【详解】
∵⊙O是等边三角形ABC的外接圆，∴∠A=∠ABC=∠ACB=60°，∴∠BDC=∠A=60°．故答案为：60°．
【点睛】
本题主要考查了圆周角定理和等边三角形的性质．解题的关键是熟练掌握圆周角定理．
14．35°；
【解析】∵A、B、C、D是⊙O上的四点，OA⊥BC，
∴弧AC=弧AB （垂径定理），
∴∠ADC= （等弧所对的圆周角是圆心角的一半）；
又∠AOB=70°，
∴∠ADC=35°．
故答案为：35°．
15．20°
【解析】
连结OC，如图，
∵D为的中点，
∴＝，
∵的度数为70，
∴的度数为140，
∴∠AOC＝140，
∴∠ABC＝∠AOC＝70，
∵AO⊥BC，
∴∠AFB＝90°，
∴∠BAF＝90°?70°＝20，
故答案为：20．
16．证明见解析
【解析】试题分析：欲证明AD=CE，只需证明即可．如图，根据平行线的性质和角平分线的定义易证得∠C=∠CAD，所以，则，故．
试题解析：如图，∵AB∥CE，
∴∠ACE=∠BAC．
又∵AC平分∠BAD，
∴∠BAC=∠DAC，
∴∠C=∠CAD，
∴，
∴，
∴，
∴AD=CE．
17．见解析
【解析】
【分析】
利用CA=CB=CO可判断△OBC和△OAC都是等边三角形，则∠BCO=∠ACO=60°，∠BOC=∠AOC=60°，根据圆周角定理得∠ADB=60°，即∠ACD=∠BCD=∠ADB，所以，然后根据圆心角、弧、弦的关系易得AD=BD=BA．
【详解】
证明：∵CA=CB=CO，
∴OB=BC=OC=OA=AC，
∴△OBC和△OAC都是等边三角形，
∴∠BCO=∠ACO=60°，∠BOC=∠AOC=60°，
∴∠AOB=120°，
∴∠ADB=60°，
∴∠ACD=∠BCD=∠ADB，
∴，
∴AD=BD=BA．
【点睛】
本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等边三角形的判定与性质．
18．详见解析.
【解析】试题分析：根据弧相等，则对应的弦相等从而证明AB=AC，则△ABC易证是等边三角形，然后根据同圆中弦相等，则对应的圆心角相等即可证得．
试题解析：证明：∵，
∴AB=AC，△ABC为等腰三角形（相等的弧所对的弦相等）
∵∠ACB=60°
∴△ABC为等边三角形，AB=BC=CA
∴∠AOB=∠BOC=∠COA（相等的弦所对的圆心角相等）
19．（1）详见解析；（2）.
【解析】
【分析】
（1）根据圆周角定理求得AD⊥BC，根据等腰三角形三线合一的性质即可证得结论；
（2）先求得∠E=∠C，根据等角对等边求得BD=DC=DE=3，进而求得AD=1，然后根据勾股定理求得AB，即可求得圆的半径.
【详解】
（1）证明：∵AB是圆O的直径，
∴AD⊥BC，
∵AB=AC，
∴BD=DC；
（2）解：∵AB=AC，
∠B=∠C，
∵∠B=∠E，
∴∠E=∠C，
∴BD=DC=DE=3，
∵BD-AD=2，
∴AD=1，
在RT△ABD中，AB=，
∴⊙O的半径为.
【点睛】
本题考查了圆周角定理，等腰三角形的判定和性质，勾股定理的应用，熟练掌握性质定理是解题的关键．
20．（1）见解析；（2）6
【解析】
【分析】
（1）欲证明AD∥EC，只要证明∠ACE=∠DAC即可；
（2）当四边形ACBE是矩形时，∠ACB=90°，根据等腰三角形的性质即可解决问题；
【详解】
（1）证明：∵AC平分∠BAD，
∴∠BAC=∠DAC，
∵∠E=∠BAC，
∴∠E=∠DAC
∵BE∥AC，
∴∠E=∠ACE，
∴∠ACE=∠DAC，
∴AD∥EC．
（2）当四边形ACBE是矩形时，∠ACB=90°，
∴∠ACB=∠ACD=90°，
∵∠BAC=∠DAC，
∴∠ABD=∠D，
∴AB=AD，
∴BC=CD=6，
故答案为6．
【点睛】
本题考查圆周角定理、矩形的性质、等腰三角形的判定和性质等知识，解题的关键是熟练掌握基本知识．
21．（1）证明见解析（2）3
【解析】
【分析】
（1）连接，由为直径可知，又因为，由等腰三角形的底边“三线合一”证明结论；
（2）连接，则为的中位线，，已知，即可知的长即为点到直线的距离.
【详解】
（1）如图，连接CD，
∵BC是⊙O的直径，
∴∠BDC=90°.
∴CD⊥AB，
又∵AC=BC，
∴AD=BD，即点D是AB的中点.
（2）如图，连接OD，
∵AD=BD，OB=OC，
∴DO是△ABC的中位线.
∴DO∥AC，OD=AC=3.
又∵DE⊥AC，
∴DE⊥DO.
∴点O到直线DE的距离为3．
【点睛】
此题考查了圆周角定理、等腰三角形的性质以及三角形中位线的性质.此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用.
22．(1)证明见解析；(2)四边形FCDE的最大面积是8.
【解析】
【分析】
（1）连接FA，根据垂直的定义得到EF⊥AB，得到BF=AF，推出BF=ED，根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到∠B=∠AED，得到DE∥BC，推出四边形形FCDE，得到E到BC的距离最大时，四边形FCDE的面积最大，即点A到DE的距离最大，推出当A为的中点时，于是得到结论．
【详解】
(1)连接FA,
∵∠FEB=90°,
∴EF⊥AB,
∵BE=AE,
∴BF=AF,
∵∠FEA=∠FEB=90°,
∴AF是☉O的直径,
∴AF=DE,
∴BF=ED,
在Rt△EFB与Rt△ADE中,
∴Rt△EFB≌Rt△ADE.
(2)∵Rt△EFB≌Rt△ADE,
∴∠B=∠AED,
∴DE∥BC,
∵ED为☉O的直径,
AC⊥AB,
∵EF⊥AB,
∴EF∥CD,
∴四边形FCDE是平行四边形,
∴E到BC的距离最大时,四边形FCDE的面积最大,即点A到DE的距离最大,
∴当A为的中点时,点A到DE的距离最大是2,
∴四边形FCDE的最大面积=4×2=8.
【点睛】
本题考查了圆周角定理，平行四边形的判定和性质，全等三角形的判定和性质，等腰三角形的性质，正确的作出辅助线是解题的关键．