3.7 正多边形同步课时作业
图片预览

文档简介
3.7 正多边形同步课时作业
姓名:___________班级:___________考号:___________
一、选择题
1.一个正六边形的半径为R,边心距为r,那么R与r的关系是( )
A. r=R B. r=R C. r=R D. r=R
2.半径为r的圆的内接正三角形的边长是( )
A. 2r B. C. D.
3.正三角形的边心距、半径和高的比是( )
A. 1:2:3 B. 1:: C. 1::3 D. 1:2:
4.如图,以正五边形ABCDE的对角线AC为边作正方形ACFG,使点B落在正方形ACFG外,则的大小为
A. B. C. D.
5.如图,雯雯开了一家品牌手机体验店,想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张.体验店平面图是长9米、宽7米的矩形,通道宽2米,桌子的边长为1米;摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,则体验区可以摆放桌子(?? )
A. 4张 B. 5张 C. 6张 D. 7张
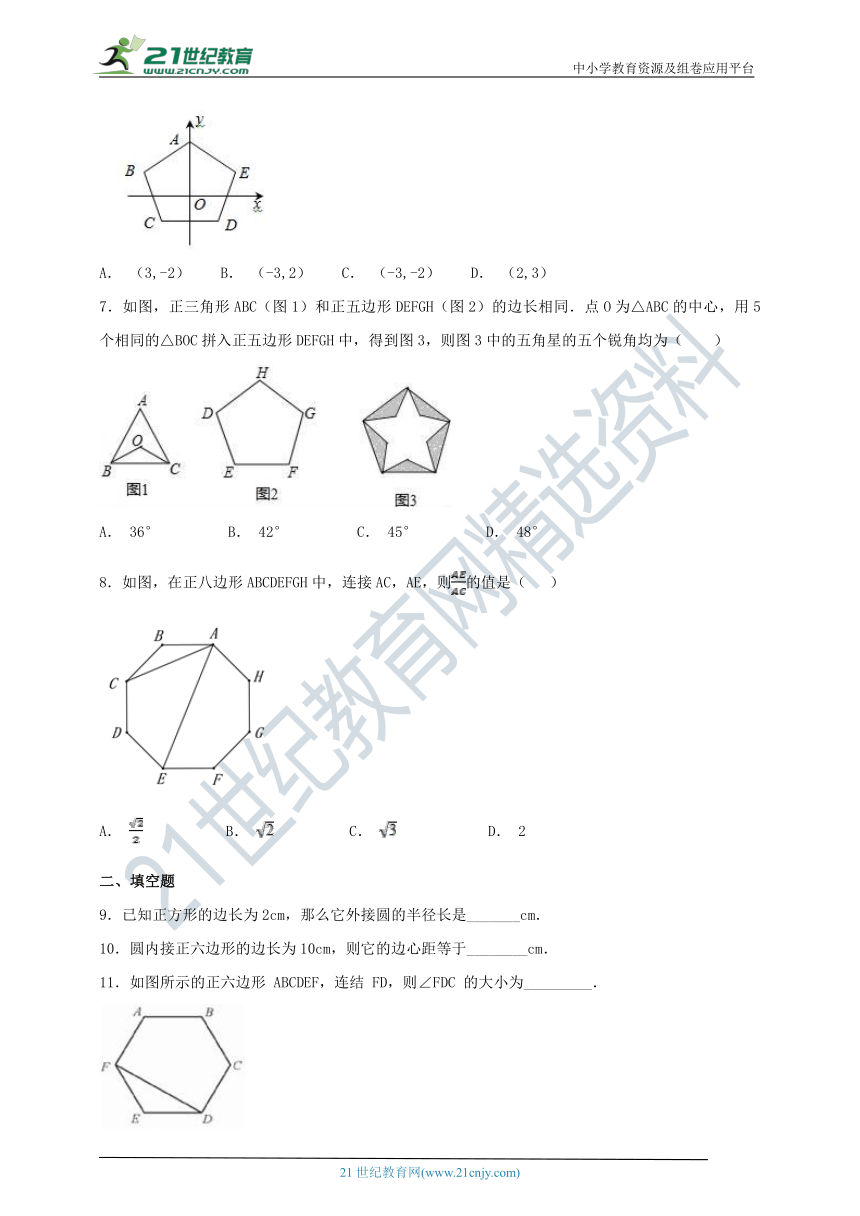
6.如图,正五边形ABCDE的顶点A在y轴上,边CD∥x轴,若点E坐标为(3,2),则点B的坐标为( )
A. (3,-2) B. (-3,2) C. (-3,-2) D. (2,3)
7.如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
A. 36° B. 42° C. 45° D. 48°
8.如图,在正八边形ABCDEFGH中,连接AC,AE,则的值是( )
A. B. C. D. 2
二、填空题
9.已知正方形的边长为2cm,那么它外接圆的半径长是_______cm.
10.圆内接正六边形的边长为10cm,则它的边心距等于________cm.
11.如图所示的正六边形 ABCDEF,连结 FD,则∠FDC 的大小为_________.
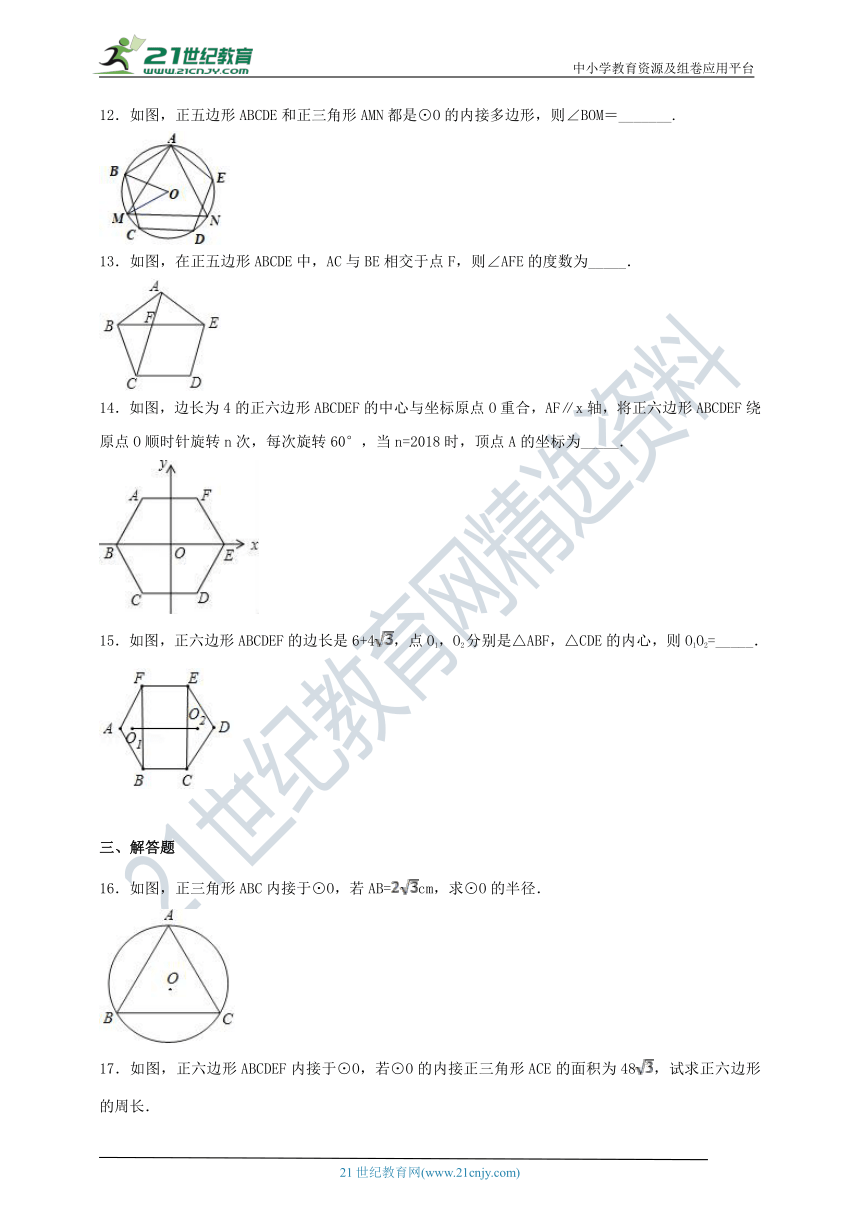
12.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=_______.
13.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为_____.
14.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2018时,顶点A的坐标为_____.
15.如图,正六边形ABCDEF的边长是6+4,点O1,O2分别是△ABF,△CDE的内心,则O1O2=_____.
三、解答题
16.如图,正三角形ABC内接于⊙O,若AB=cm,求⊙O的半径.
17.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48,试求正六边形的周长.
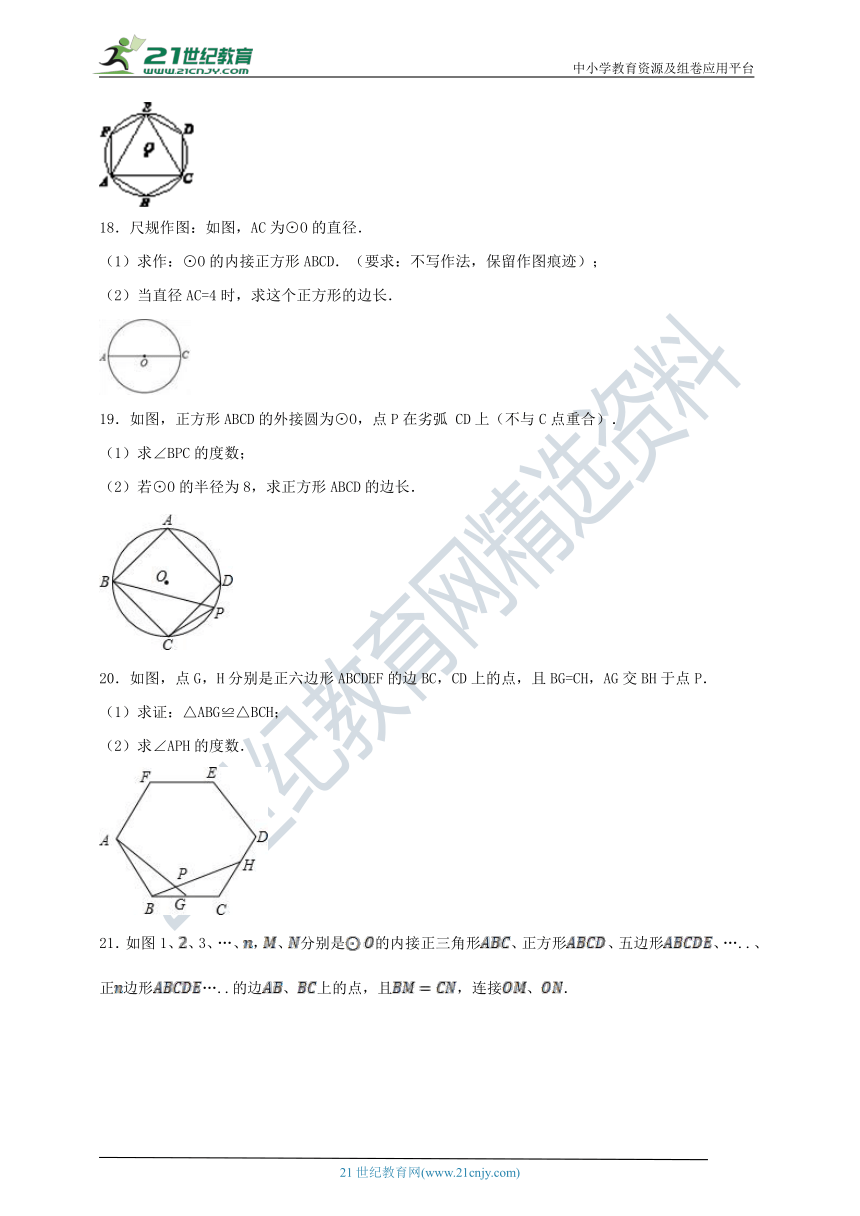
18.尺规作图:如图,AC为⊙O的直径.
(1)求作:⊙O的内接正方形ABCD.(要求:不写作法,保留作图痕迹);
(2)当直径AC=4时,求这个正方形的边长.
19.如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
20.如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
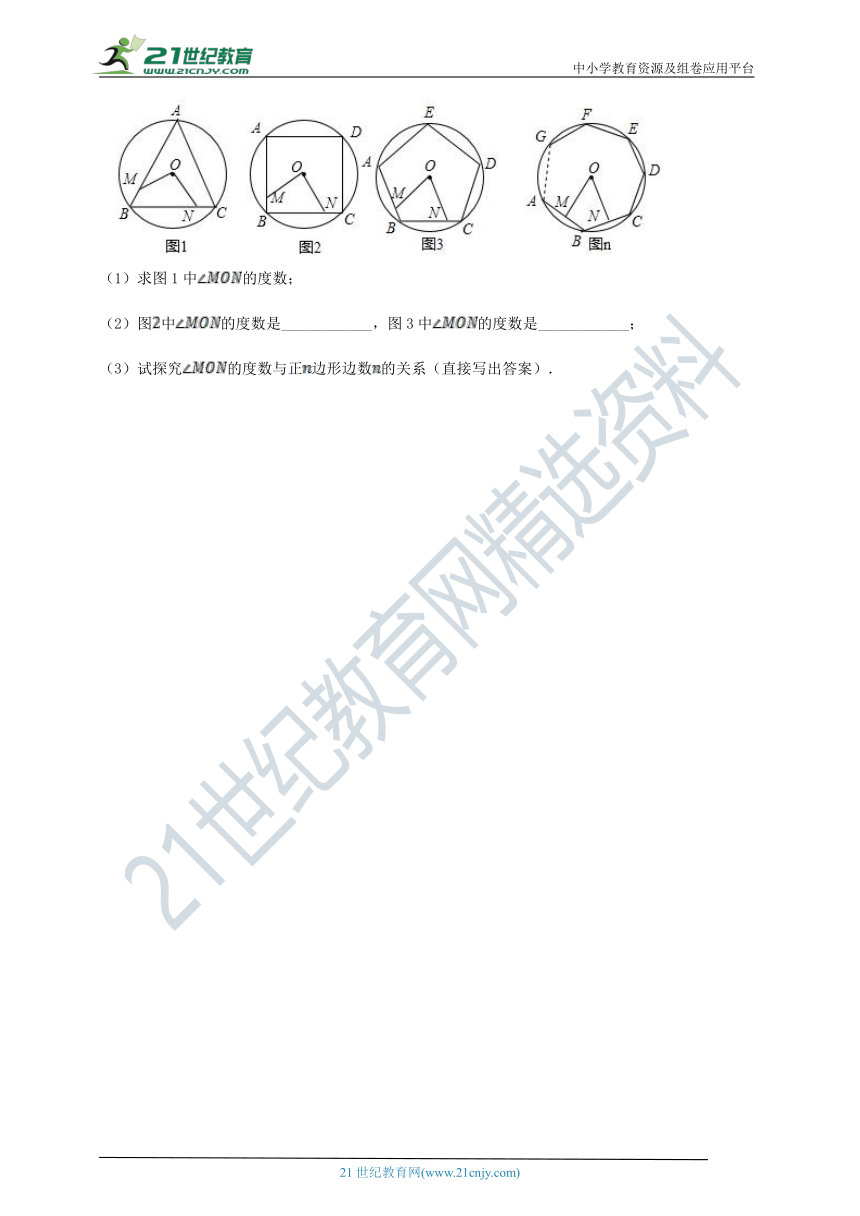
21.如图1、、3、…、,、分别是的内接正三角形、正方形、五边形、…..、正边形…..的边、上的点,且,连接、.
(1)求图1中的度数;
(2)图中的度数是____________,图3中的度数是____________;
(3)试探究的度数与正边形边数的关系(直接写出答案).
参考答案
1.A
【解析】
【分析】
求出正六边形的边心距(用R表示),根据“接近度”的定义即可解决问题.
【详解】
解:∵正六边形的半径为R,
∴边心距r=R,
故选:A.
【点睛】
本题考查正多边形与圆的共线,等边三角形高的计算,记住等边三角形的高h=a(a是等边三角形的边长),理解题意是解题的关键,属于中考常考题型.
2.B
【解析】
【分析】
根据题意画出图形,作出辅助线,利用垂径定理及勾股定理解答即可.
【详解】
如图所示,OB=OA=r;
,
∵△ABC是正三角形,
由于正三角形的中心就是圆的圆心,
且正三角形三线合一,
所以BO是∠ABC的平分线;
∠OBD=60°×=30°,
BD=r?cos30°=;
根据垂径定理,BC=2×=r.
故选B.
【点睛】
本题主要考查了正多边形和圆,正三角形的性质,熟练掌握等边三角形的性质是解题的关键,根据圆的内接正三角形的特点,求出内心到每个顶点的距离,可求出内接正三角形的边长.
3.A
【解析】【分析】如图,O为正△ABC的中心,AD为△ABC的边BC上的高,则OD为边心距,OA为半径,根据正三角形的性质以及含30度角的直角三角形的性质进行推导即可得.
【详解】如图,O为正△ABC的中心,AD为△ABC的边BC上的高,
则OD为边心距,OA为半径,
∴∠BAD=30°,
又∵AO=BO,
∴∠ABO=∠BAD=30°,
∴∠OBD=60°-30°=30°,
在Rt△OBD中,
BO=2DO,
即AO=2DO,
∴OD:OA:AD=1:2:3.
故选A.
【点睛】本题考查了等边三角形性质,正三角形的中心,含30度角的直角三角形等知识,根据题意画出图形,结合图形应用相关知识进行解答是关键.
4.A
【解析】
【分析】
首先根据正五边形的性质得出∠B=∠BAE=108°,AB=BC,利用等边对等角以及三角形内角和定理求出∠BAC=∠BCA=(180°-∠B)=36°,则∠CAE=∠BAE-∠BAC=72°.再根据正方形的性质得出∠CAG=90°,代入∠EAG=∠CAG-∠CAE即可求解.
【详解】
∵五边形ABCDE是正五边形,
∴∠B=∠BAE=180°-=108°,AB=BC,
∴∠BAC=∠BCA=(180°-∠B)=36°,
∴∠CAE=∠BAE-∠BAC=108°-36°=72°.
∵四边形ACFG是正方形,
∴∠CAG=90°,
∠EAG=∠CAG-∠CAE=90°-72°=18°.
故选A.
【点睛】
本题考查了正五边形、正方形的性质,等腰三角形的性质以及三角形内角和定理,求出∠CAE的度数是解题的关键.
5.A
【解析】分析:画出桌子的外接四边形是矩形,分别求出矩形的长和宽,再根据摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,求出每张桌子占的最大面积,用总面积除以每张桌子占的最大面积,就可求出结果.
详解:如图
根据题意可知:∠AEC=30°,CE=CD=1
AC=GF=BD
在Rt△AEC中,AE=CEcos30°=
AC=
∴AG=2AE=,AB=2AC+CD=1+1=2
∵摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,
一张桌子所占的总面积为3(+)≈10
体验区的总面积为7×7=49
49÷10≈4
体验区可以摆放桌子4张
故选:A
点睛:本题主要考查了正多边形的相关计算,作出正六边形的外接矩形是解题关键.
6.B
【解析】分析:由正五边形ABCDE的顶点A在y轴上,边CD∥x轴,得到B和E关于y轴对称,即可得到结论.
详解:∵正五边形ABCDE的顶点A在y轴上,边CD∥x轴,∴B和E关于y轴对称.
∵点E坐标为(3,2),∴点B坐标为(-3,2).故选B.
点睛:本题考查了正多边形的性质,解题的关键是得出B和E关于y轴对称.
7.D
【解析】分析:根据图1先求出正三角形ABC内大钝角的度数是120°,则两锐角的和等于60°,正五边形的内角和是540°,求出每一个内角的度数,然后解答即可.
详解:如图,图1先求出正三角形ABC内大钝角的度数是180°-30°×2=120°,
180°-120°=60°,
60°÷2=30°,
正五边形的每一个内角=(5-2)?180°÷5=108°,
∴图3中的五角星的五个锐角均为:108°-60°=48°.
故选:D.
点睛:本题主要考查了多边形的内角与外角的性质,仔细观察图形是解题的关键,难度中等.
8.B
【解析】【分析】连接AG、GE、EC,易知四边形ACEG为正方形,根据正方形的性质即可求解.
【详解】连接AG、GE、EC,
∵ABCDEFGH是正八边形,
∴AB=BC=CD=DE=EF=FG=GH=HA,∠B=∠BCD=∠D=∠F =∠H =135°,
∴△ABC≌△CDE≌△EFG≌△GHA(SAS),
∴AC=CE=EG=GA,∴四边形ACEG是菱形,
∵AB=BC,∠B=135°,
∴∠ACB=22.5°,
同理∠ECD=22.5°,
∴∠ACE=90°,
∴四边形ACEG为正方形,
∴,
故选B.
【点睛】本题考查了正多边形的性质,正确作出辅助线是关键.
9.
【解析】分析:运用正方形的性质,以及与外接圆的关系,可求出外接圆半径.
详解:∵正方形的边长为2,
由中心角只有四个可得出:
∴中心角是:
正方形的外接圆半径是:sin∠AOC
∵
∴
故答案为:
点睛:考查正多边形和圆,涉及垂径定理,解直角三角形,比较简单.
10..
【解析】试题解析:如图所示,连接OB、OC,过O作OG⊥BC于G,
∵此多边形是正六边形,
∴△OBC是等边三角形,
∴边心距
故答案为:
11.90°
【解析】分析:首先求得正六边形的内角的度数,根据等腰三角形的性质即可得到结论.
详解:∵在正六边形ABCDEF中,∠E=∠EDC=120°,
∵EF=DE,
∴∠EDF=∠EFD=30°,
∴∠FDC=90°,
故答案为:90°
点睛:此题考查了正多边形和圆.等腰三角形的性质,此题难度不大,注意数形结合思想的应用.
12.48°
【解析】分析:连接OA,分别求出正五边形ABCDE和正三角形AMN的中心角,结合图形计算即可.
详解:连接OA,
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠BOM=∠AOM-∠AOB=48°,
故答案为:48°.
点睛:本题考查的是正多边形与圆的有关计算,掌握正多边形的中心角的计算公式是解题的关键.
13.72°
【解析】
【分析】首先根据正五边形的性质得到AB=BC=AE,∠ABC=∠BAE=108°,然后利用三角形内角和定理得∠BAC=∠BCA=∠ABE=∠AEB=(180°?108°)÷2=36°,最后利用三角形的外角的性质得到∠AFE=∠BAC+∠ABE=72°.
【详解】∵五边形ABCDE为正五边形,
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BAC=∠BCA=∠ABE=∠AEB=(180°?108°)÷2=36°,
∴∠AFE=∠BAC+∠ABE=72°,
故答案为:72°.
【点睛】本题考查的是正多边形和圆,利用数形结合求解是解答此题的关键
14.(4,0).
【解析】分析:由正六边形的中心角是60°可知,将正六边形ABCDEF绕原点O顺时针旋转2018次时,点A所在的位置与点E点所在的位置重合.
详解:连接OA、OC、OD、OF,
∵六边形ABCDEF是正六边形,
∴∠AOF=∠FOE=∠EOD=∠DOC=∠COB=∠BOA=60°,
∵将正六边形ABCDEF绕原点O顺时针旋转,每次旋转60°,
∴点A旋转6次回到点A,
2018÷6=336…2,
∴正六边形ABCDEF绕原点O顺时针旋转2018次,与点E重合,
∴顶点A的坐标为(4,0),
故答案为(4,0).
点睛:此题主要考查了图形类探索与规律,正六边形的性质,坐标与图形的性质-旋转,此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
15.9+4
【解析】【分析】如图,设△AFB的内切圆的半径为r,过A作AM⊥BF于M,连接O1F、O1A、O1B,解直角三角形求出AM、FM、BM,根据三角形的面积求出r,即可求出答案.
【详解】如图,过A作AM⊥BF于M,连接O1F、O1A、O1B,
∵六边形ABCDEF是正六边形,
∴∠A==120°,AF=AB,
∴∠AFB=∠ABF=×(180°﹣120°)=30°,
∴△AFB边BF上的高AM=AF=×(6+4)=3+2,
FM=BM=AM=3+6,
∴BF=3+6+3+6=12+6,
设△AFB的内切圆的半径为r,
∵S△AFB=,
∴×(3+2)×(3+6)
=×(6+4)×r+×(6+4)×r+×(12+6)×r,
解得:r=,
即O1M=r=,
∴O1O2=2×+6+4=9+4,
故答案为:9+4.
【点睛】本题考查了正多边形和圆,解直角三角形,三角形面积公式,三角形的内接圆和内心等知识点,正确添加辅助线、求出△ABF的内切圆的半径是解此题的关键.
16.2cm
【解析】
【分析】
利用等边三角形的性质得出点O既是三角形内心也是外心,进而求出∠OBD=30°,BD=CD,再利用锐角函数关系得出BO即可.
【详解】
过点O作OD⊥BC于点D,连接BO,
∵正三角形ABC内接于⊙O,
∴点O即是三角形内心也是外心,
∴∠OBD=30°,BD=CD=BC=AB=,
∴cos30°===,
解得:BO=2,
即⊙O的半径为2cm.
【点睛】
考查了正多边形和圆,利用正多边形内外心的特殊关系得出∠OBD=30°,BD=CD是解题关键.
17.正六边形的周长为48.
【解析】【分析】连接OA,作OH⊥AC于点H,则∠OAH=30°. 连接OA,作OH⊥AC于点H,则∠OAH=30°. 由△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R,可求出周长.
【详解】解: 如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,AH=
=
而△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
【点睛】本题考核知识点:正多边形和圆.解题关键点:结合勾股定理求出边长.
18.(1)见解析;(2)2
【解析】试题分析:(1)过点O作出直径AC的垂线,进而得出答案;
(2)利用正方形的性质结合勾股定理得出正方形ABCD的边长.
试题解析:解:(1)如图所示:
(2)∵直径AC=4,∴OA=OB=2.∵正方形ABCD为⊙O的内接正方形,∴∠AOB=90°,∴AB==.
点睛:此题主要考查了复杂作图以及正多边形和圆,正确掌握正方形的性质是解题的关键.
19.(1)45°;(2)8
【解析】试题分析:(1)连接OB,OC,由正方形的性质知, 是等腰直角三角形,根据,由圆周角定理可以求出; (2)过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
试题解析:(1)连接OB,OC,
∵四边形ABCD为正方形,
∴∠BOC=90°,
∴∠P=∠BOC=45°;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴BE=,
∴BC=2BE=2×.
点睛:垂径定理:垂直于弦的直径平分弦并且平分弦所对的两条弧.
20.(1)证明见解析;(2)120°
【解析】试题分析:(1)根据正六边形的性质得到AB=BC,∠ABC=∠C=120°,由三角形全等的判定定理SAS即可证出△ABG≌△BCH; (2)由△ABG≌△BCH,得到∠BAG=∠HBC,然后根据三角形的内角和和对顶角的性质即可得到结果.
试题解析:(1)∵在正六边形ABCDEF中,
AB=BC,∠ABC=∠C=120°,
在△ABG与△BCH中
AB=BC,∠ABC=∠C=120°, BG=CH ,
∴△ABG≌△BCH;
(2)由(1)知:△ABG≌△BCH,
∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°.
21.(1);(2),;(3)
【解析】
试题分析:连接BO,CO那么,有:BM=CM, ∠OBM=∠OCN,BO=CO,利用SAS证明△OBM≌△OCN,同理可得,图1中的∠MON=∠BOC=120°,图2中心角等于360°÷4=90°,图3的中心角等于360°÷5=72°,所以,(1)120°,(2)90° 72°,(3)正n边形时, ∠MON=∠BOC=360°÷n, ∠MON是一定值,取特殊位置进行分析,对三个图取B与M重合,N与C重合,即可求出∠MON的值.
试题解析:(1)解法一:连接OB,OC,
∵正△ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,
∴∠BOM=∠OCN,
∴∠MON=∠BOC=120°.
解法二:连接OA,OB,
∵正△ABC内接于⊙O,
∴AB=AC,∠OAM=∠OBN=30°,∠AOB=120°,
又∵BM=CN,
∴AM=BN,
又∵OA=OB,
∴△AOM≌△BON,
∴∠AOM=∠BON,
∴∠AON=∠AOB=120°.
(2)90°, 72°.
(3)∠MON=.
姓名:___________班级:___________考号:___________
一、选择题
1.一个正六边形的半径为R,边心距为r,那么R与r的关系是( )
A. r=R B. r=R C. r=R D. r=R
2.半径为r的圆的内接正三角形的边长是( )
A. 2r B. C. D.
3.正三角形的边心距、半径和高的比是( )
A. 1:2:3 B. 1:: C. 1::3 D. 1:2:
4.如图,以正五边形ABCDE的对角线AC为边作正方形ACFG,使点B落在正方形ACFG外,则的大小为
A. B. C. D.
5.如图,雯雯开了一家品牌手机体验店,想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张.体验店平面图是长9米、宽7米的矩形,通道宽2米,桌子的边长为1米;摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,则体验区可以摆放桌子(?? )
A. 4张 B. 5张 C. 6张 D. 7张
6.如图,正五边形ABCDE的顶点A在y轴上,边CD∥x轴,若点E坐标为(3,2),则点B的坐标为( )
A. (3,-2) B. (-3,2) C. (-3,-2) D. (2,3)
7.如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
A. 36° B. 42° C. 45° D. 48°
8.如图,在正八边形ABCDEFGH中,连接AC,AE,则的值是( )
A. B. C. D. 2
二、填空题
9.已知正方形的边长为2cm,那么它外接圆的半径长是_______cm.
10.圆内接正六边形的边长为10cm,则它的边心距等于________cm.
11.如图所示的正六边形 ABCDEF,连结 FD,则∠FDC 的大小为_________.
12.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=_______.
13.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为_____.
14.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2018时,顶点A的坐标为_____.
15.如图,正六边形ABCDEF的边长是6+4,点O1,O2分别是△ABF,△CDE的内心,则O1O2=_____.
三、解答题
16.如图,正三角形ABC内接于⊙O,若AB=cm,求⊙O的半径.
17.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48,试求正六边形的周长.
18.尺规作图:如图,AC为⊙O的直径.
(1)求作:⊙O的内接正方形ABCD.(要求:不写作法,保留作图痕迹);
(2)当直径AC=4时,求这个正方形的边长.
19.如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
20.如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
21.如图1、、3、…、,、分别是的内接正三角形、正方形、五边形、…..、正边形…..的边、上的点,且,连接、.
(1)求图1中的度数;
(2)图中的度数是____________,图3中的度数是____________;
(3)试探究的度数与正边形边数的关系(直接写出答案).
参考答案
1.A
【解析】
【分析】
求出正六边形的边心距(用R表示),根据“接近度”的定义即可解决问题.
【详解】
解:∵正六边形的半径为R,
∴边心距r=R,
故选:A.
【点睛】
本题考查正多边形与圆的共线,等边三角形高的计算,记住等边三角形的高h=a(a是等边三角形的边长),理解题意是解题的关键,属于中考常考题型.
2.B
【解析】
【分析】
根据题意画出图形,作出辅助线,利用垂径定理及勾股定理解答即可.
【详解】
如图所示,OB=OA=r;
,
∵△ABC是正三角形,
由于正三角形的中心就是圆的圆心,
且正三角形三线合一,
所以BO是∠ABC的平分线;
∠OBD=60°×=30°,
BD=r?cos30°=;
根据垂径定理,BC=2×=r.
故选B.
【点睛】
本题主要考查了正多边形和圆,正三角形的性质,熟练掌握等边三角形的性质是解题的关键,根据圆的内接正三角形的特点,求出内心到每个顶点的距离,可求出内接正三角形的边长.
3.A
【解析】【分析】如图,O为正△ABC的中心,AD为△ABC的边BC上的高,则OD为边心距,OA为半径,根据正三角形的性质以及含30度角的直角三角形的性质进行推导即可得.
【详解】如图,O为正△ABC的中心,AD为△ABC的边BC上的高,
则OD为边心距,OA为半径,
∴∠BAD=30°,
又∵AO=BO,
∴∠ABO=∠BAD=30°,
∴∠OBD=60°-30°=30°,
在Rt△OBD中,
BO=2DO,
即AO=2DO,
∴OD:OA:AD=1:2:3.
故选A.
【点睛】本题考查了等边三角形性质,正三角形的中心,含30度角的直角三角形等知识,根据题意画出图形,结合图形应用相关知识进行解答是关键.
4.A
【解析】
【分析】
首先根据正五边形的性质得出∠B=∠BAE=108°,AB=BC,利用等边对等角以及三角形内角和定理求出∠BAC=∠BCA=(180°-∠B)=36°,则∠CAE=∠BAE-∠BAC=72°.再根据正方形的性质得出∠CAG=90°,代入∠EAG=∠CAG-∠CAE即可求解.
【详解】
∵五边形ABCDE是正五边形,
∴∠B=∠BAE=180°-=108°,AB=BC,
∴∠BAC=∠BCA=(180°-∠B)=36°,
∴∠CAE=∠BAE-∠BAC=108°-36°=72°.
∵四边形ACFG是正方形,
∴∠CAG=90°,
∠EAG=∠CAG-∠CAE=90°-72°=18°.
故选A.
【点睛】
本题考查了正五边形、正方形的性质,等腰三角形的性质以及三角形内角和定理,求出∠CAE的度数是解题的关键.
5.A
【解析】分析:画出桌子的外接四边形是矩形,分别求出矩形的长和宽,再根据摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,求出每张桌子占的最大面积,用总面积除以每张桌子占的最大面积,就可求出结果.
详解:如图
根据题意可知:∠AEC=30°,CE=CD=1
AC=GF=BD
在Rt△AEC中,AE=CEcos30°=
AC=
∴AG=2AE=,AB=2AC+CD=1+1=2
∵摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,
一张桌子所占的总面积为3(+)≈10
体验区的总面积为7×7=49
49÷10≈4
体验区可以摆放桌子4张
故选:A
点睛:本题主要考查了正多边形的相关计算,作出正六边形的外接矩形是解题关键.
6.B
【解析】分析:由正五边形ABCDE的顶点A在y轴上,边CD∥x轴,得到B和E关于y轴对称,即可得到结论.
详解:∵正五边形ABCDE的顶点A在y轴上,边CD∥x轴,∴B和E关于y轴对称.
∵点E坐标为(3,2),∴点B坐标为(-3,2).故选B.
点睛:本题考查了正多边形的性质,解题的关键是得出B和E关于y轴对称.
7.D
【解析】分析:根据图1先求出正三角形ABC内大钝角的度数是120°,则两锐角的和等于60°,正五边形的内角和是540°,求出每一个内角的度数,然后解答即可.
详解:如图,图1先求出正三角形ABC内大钝角的度数是180°-30°×2=120°,
180°-120°=60°,
60°÷2=30°,
正五边形的每一个内角=(5-2)?180°÷5=108°,
∴图3中的五角星的五个锐角均为:108°-60°=48°.
故选:D.
点睛:本题主要考查了多边形的内角与外角的性质,仔细观察图形是解题的关键,难度中等.
8.B
【解析】【分析】连接AG、GE、EC,易知四边形ACEG为正方形,根据正方形的性质即可求解.
【详解】连接AG、GE、EC,
∵ABCDEFGH是正八边形,
∴AB=BC=CD=DE=EF=FG=GH=HA,∠B=∠BCD=∠D=∠F =∠H =135°,
∴△ABC≌△CDE≌△EFG≌△GHA(SAS),
∴AC=CE=EG=GA,∴四边形ACEG是菱形,
∵AB=BC,∠B=135°,
∴∠ACB=22.5°,
同理∠ECD=22.5°,
∴∠ACE=90°,
∴四边形ACEG为正方形,
∴,
故选B.
【点睛】本题考查了正多边形的性质,正确作出辅助线是关键.
9.
【解析】分析:运用正方形的性质,以及与外接圆的关系,可求出外接圆半径.
详解:∵正方形的边长为2,
由中心角只有四个可得出:
∴中心角是:
正方形的外接圆半径是:sin∠AOC
∵
∴
故答案为:
点睛:考查正多边形和圆,涉及垂径定理,解直角三角形,比较简单.
10..
【解析】试题解析:如图所示,连接OB、OC,过O作OG⊥BC于G,
∵此多边形是正六边形,
∴△OBC是等边三角形,
∴边心距
故答案为:
11.90°
【解析】分析:首先求得正六边形的内角的度数,根据等腰三角形的性质即可得到结论.
详解:∵在正六边形ABCDEF中,∠E=∠EDC=120°,
∵EF=DE,
∴∠EDF=∠EFD=30°,
∴∠FDC=90°,
故答案为:90°
点睛:此题考查了正多边形和圆.等腰三角形的性质,此题难度不大,注意数形结合思想的应用.
12.48°
【解析】分析:连接OA,分别求出正五边形ABCDE和正三角形AMN的中心角,结合图形计算即可.
详解:连接OA,
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠BOM=∠AOM-∠AOB=48°,
故答案为:48°.
点睛:本题考查的是正多边形与圆的有关计算,掌握正多边形的中心角的计算公式是解题的关键.
13.72°
【解析】
【分析】首先根据正五边形的性质得到AB=BC=AE,∠ABC=∠BAE=108°,然后利用三角形内角和定理得∠BAC=∠BCA=∠ABE=∠AEB=(180°?108°)÷2=36°,最后利用三角形的外角的性质得到∠AFE=∠BAC+∠ABE=72°.
【详解】∵五边形ABCDE为正五边形,
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BAC=∠BCA=∠ABE=∠AEB=(180°?108°)÷2=36°,
∴∠AFE=∠BAC+∠ABE=72°,
故答案为:72°.
【点睛】本题考查的是正多边形和圆,利用数形结合求解是解答此题的关键
14.(4,0).
【解析】分析:由正六边形的中心角是60°可知,将正六边形ABCDEF绕原点O顺时针旋转2018次时,点A所在的位置与点E点所在的位置重合.
详解:连接OA、OC、OD、OF,
∵六边形ABCDEF是正六边形,
∴∠AOF=∠FOE=∠EOD=∠DOC=∠COB=∠BOA=60°,
∵将正六边形ABCDEF绕原点O顺时针旋转,每次旋转60°,
∴点A旋转6次回到点A,
2018÷6=336…2,
∴正六边形ABCDEF绕原点O顺时针旋转2018次,与点E重合,
∴顶点A的坐标为(4,0),
故答案为(4,0).
点睛:此题主要考查了图形类探索与规律,正六边形的性质,坐标与图形的性质-旋转,此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
15.9+4
【解析】【分析】如图,设△AFB的内切圆的半径为r,过A作AM⊥BF于M,连接O1F、O1A、O1B,解直角三角形求出AM、FM、BM,根据三角形的面积求出r,即可求出答案.
【详解】如图,过A作AM⊥BF于M,连接O1F、O1A、O1B,
∵六边形ABCDEF是正六边形,
∴∠A==120°,AF=AB,
∴∠AFB=∠ABF=×(180°﹣120°)=30°,
∴△AFB边BF上的高AM=AF=×(6+4)=3+2,
FM=BM=AM=3+6,
∴BF=3+6+3+6=12+6,
设△AFB的内切圆的半径为r,
∵S△AFB=,
∴×(3+2)×(3+6)
=×(6+4)×r+×(6+4)×r+×(12+6)×r,
解得:r=,
即O1M=r=,
∴O1O2=2×+6+4=9+4,
故答案为:9+4.
【点睛】本题考查了正多边形和圆,解直角三角形,三角形面积公式,三角形的内接圆和内心等知识点,正确添加辅助线、求出△ABF的内切圆的半径是解此题的关键.
16.2cm
【解析】
【分析】
利用等边三角形的性质得出点O既是三角形内心也是外心,进而求出∠OBD=30°,BD=CD,再利用锐角函数关系得出BO即可.
【详解】
过点O作OD⊥BC于点D,连接BO,
∵正三角形ABC内接于⊙O,
∴点O即是三角形内心也是外心,
∴∠OBD=30°,BD=CD=BC=AB=,
∴cos30°===,
解得:BO=2,
即⊙O的半径为2cm.
【点睛】
考查了正多边形和圆,利用正多边形内外心的特殊关系得出∠OBD=30°,BD=CD是解题关键.
17.正六边形的周长为48.
【解析】【分析】连接OA,作OH⊥AC于点H,则∠OAH=30°. 连接OA,作OH⊥AC于点H,则∠OAH=30°. 由△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R,可求出周长.
【详解】解: 如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,AH=
=
而△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
【点睛】本题考核知识点:正多边形和圆.解题关键点:结合勾股定理求出边长.
18.(1)见解析;(2)2
【解析】试题分析:(1)过点O作出直径AC的垂线,进而得出答案;
(2)利用正方形的性质结合勾股定理得出正方形ABCD的边长.
试题解析:解:(1)如图所示:
(2)∵直径AC=4,∴OA=OB=2.∵正方形ABCD为⊙O的内接正方形,∴∠AOB=90°,∴AB==.
点睛:此题主要考查了复杂作图以及正多边形和圆,正确掌握正方形的性质是解题的关键.
19.(1)45°;(2)8
【解析】试题分析:(1)连接OB,OC,由正方形的性质知, 是等腰直角三角形,根据,由圆周角定理可以求出; (2)过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
试题解析:(1)连接OB,OC,
∵四边形ABCD为正方形,
∴∠BOC=90°,
∴∠P=∠BOC=45°;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴BE=,
∴BC=2BE=2×.
点睛:垂径定理:垂直于弦的直径平分弦并且平分弦所对的两条弧.
20.(1)证明见解析;(2)120°
【解析】试题分析:(1)根据正六边形的性质得到AB=BC,∠ABC=∠C=120°,由三角形全等的判定定理SAS即可证出△ABG≌△BCH; (2)由△ABG≌△BCH,得到∠BAG=∠HBC,然后根据三角形的内角和和对顶角的性质即可得到结果.
试题解析:(1)∵在正六边形ABCDEF中,
AB=BC,∠ABC=∠C=120°,
在△ABG与△BCH中
AB=BC,∠ABC=∠C=120°, BG=CH ,
∴△ABG≌△BCH;
(2)由(1)知:△ABG≌△BCH,
∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°.
21.(1);(2),;(3)
【解析】
试题分析:连接BO,CO那么,有:BM=CM, ∠OBM=∠OCN,BO=CO,利用SAS证明△OBM≌△OCN,同理可得,图1中的∠MON=∠BOC=120°,图2中心角等于360°÷4=90°,图3的中心角等于360°÷5=72°,所以,(1)120°,(2)90° 72°,(3)正n边形时, ∠MON=∠BOC=360°÷n, ∠MON是一定值,取特殊位置进行分析,对三个图取B与M重合,N与C重合,即可求出∠MON的值.
试题解析:(1)解法一:连接OB,OC,
∵正△ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,
∴∠BOM=∠OCN,
∴∠MON=∠BOC=120°.
解法二:连接OA,OB,
∵正△ABC内接于⊙O,
∴AB=AC,∠OAM=∠OBN=30°,∠AOB=120°,
又∵BM=CN,
∴AM=BN,
又∵OA=OB,
∴△AOM≌△BON,
∴∠AOM=∠BON,
∴∠AON=∠AOB=120°.
(2)90°, 72°.
(3)∠MON=.
同课章节目录
