3.8 弧长及扇形的面积同步课时作业(2)
文档属性
| 名称 | 3.8 弧长及扇形的面积同步课时作业(2) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-12 15:01:15 | ||
图片预览



文档简介
3.8 弧长及扇形的面积同步课时作业(2)
姓名:___________班级:___________考号:___________
一、选择题
1.右图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
A. 5πcm2 B. 10πcm2 C. 15πcm2 D. 20πcm2
2.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
A. B. C. D.
3.如图,一张半径为1的圆形纸片在边长为的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
A. B. C. D.
4.如图,线段,分别以A、B为圆心,以AB的长为半径作弧,两弧交于C、D两点,则阴影部分的面积为
A. B. C. D.
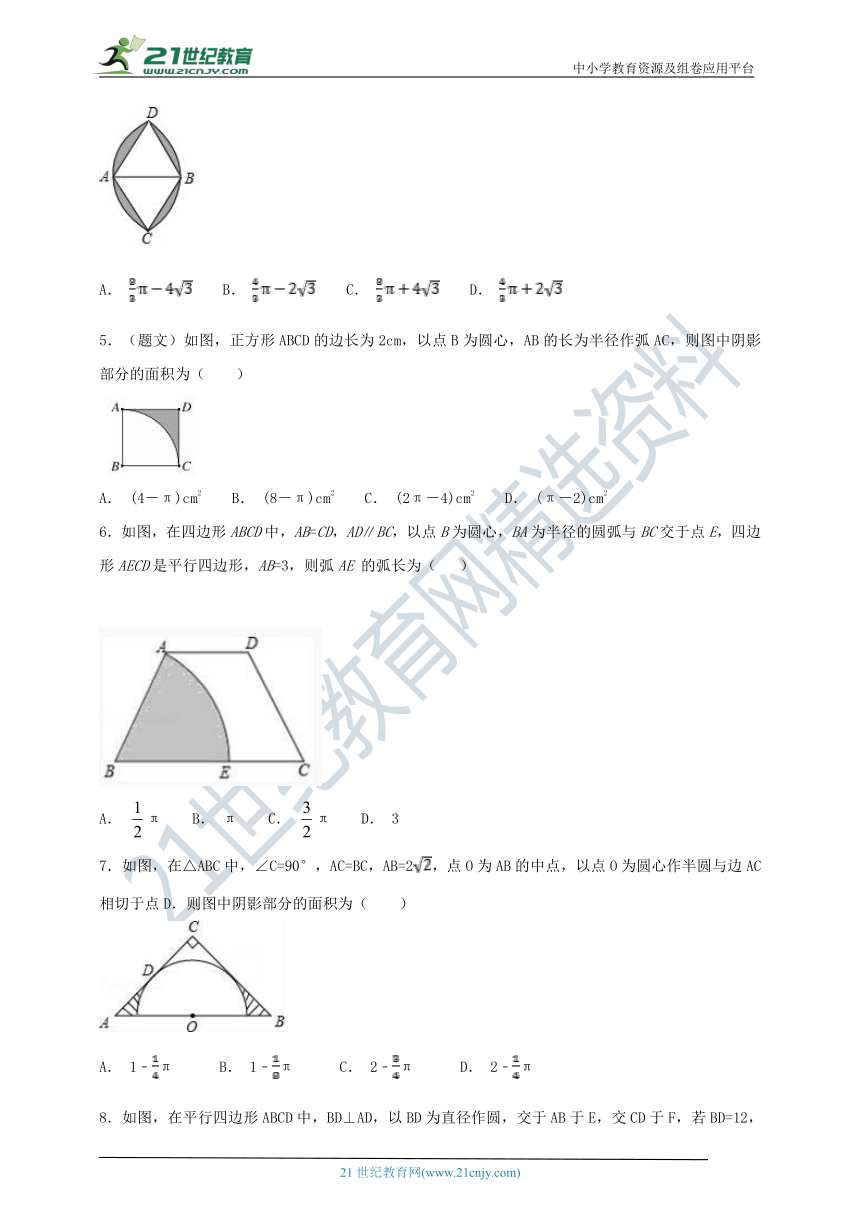
5.(题文)如图,正方形ABCD的边长为2cm,以点B为圆心,AB的长为半径作弧AC,则图中阴影部分的面积为( )
A. (4-π)cm2 B. (8-π)cm2 C. (2π-4)cm2 D. (π-2)cm2
6.如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=3,则弧AE 的弧长为( )
A. π B. π C. π D. 3
7.如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )
A. 1﹣π B. 1﹣π C. 2﹣π D. 2﹣π
8.如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为( )
A. 12 B. π C. D. π
9.如图,边长为1的正方形ABCD绕点A逆时针旋转后得到正方形,边与CD交于点O,则图中阴影部分的面积是
A. B. C. D.
二、填空题
10.如图,在矩形ABCD中,以AD为直径的半圆与边BC相切于点E,若AD=4,则图中的阴影部分的面积为 .
11.如图,在扇形AOB中,,,过点C作于点D,以CD为边向右作正方形CDEF,若,则阴影部分的面积是______结果保留.
12.如图是圆心角为 30°,半径分别是 1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为 S1、
S2、S3、…,则 S3=__________,Sn=__________.结果保留 π)
13.如图,将半径为2,圆心角为的扇形OAB绕点A逆时针旋转,点O,B的对应点分别为,,连接,则图中阴影部分的面积是______.
14.如图,在中,,,以AB中点D为圆心,作圆心角为的扇形DEF,点C恰好在弧EF上,则图中阴影部分面积为______.
15.如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是_____(结果保留π)
16.如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
三、解答题
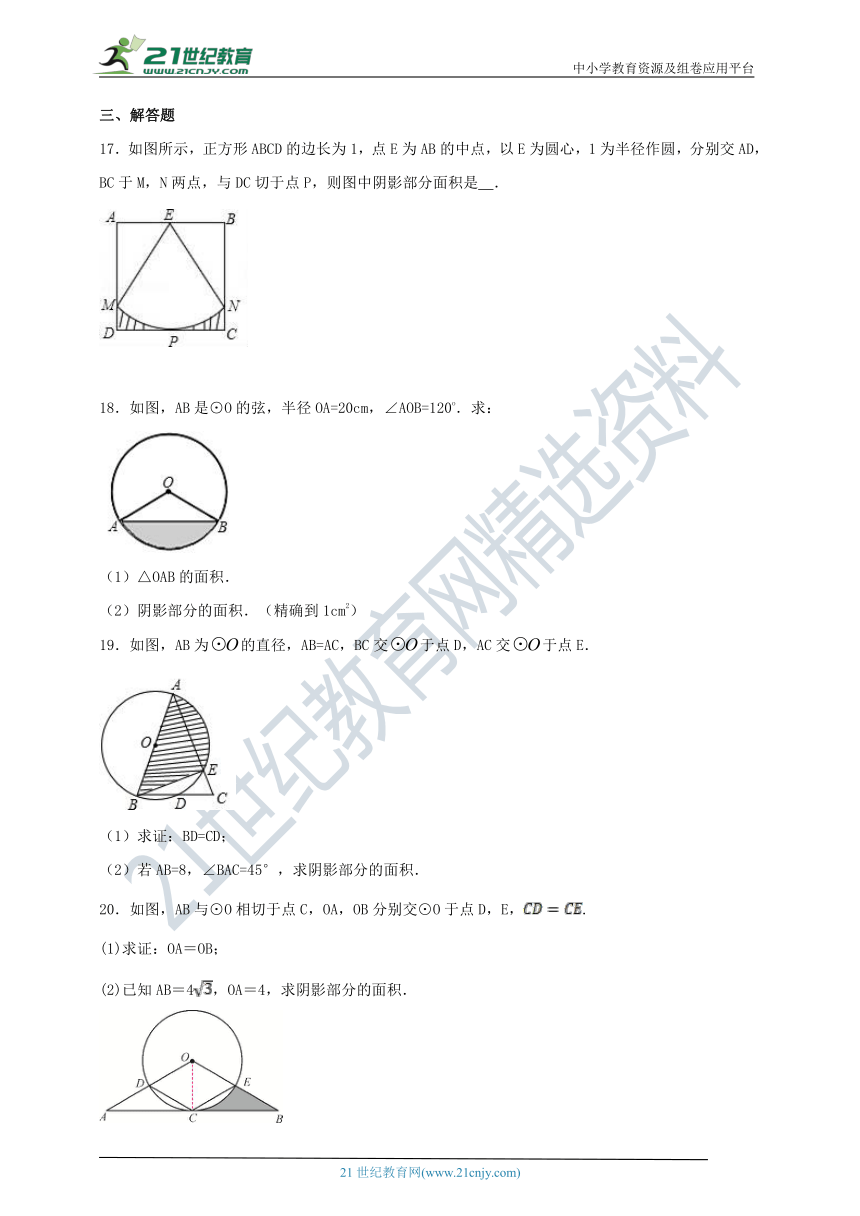
17.如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是 .
18.如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120o.求:
(1)△OAB的面积.
(2)阴影部分的面积.(精确到1cm2)
19.如图,AB为的直径,AB=AC,BC交于点D,AC交于点E.
(1)求证:BD=CD;
(2)若AB=8,∠BAC=45°,求阴影部分的面积.
20.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,.
(1)求证:OA=OB;
(2)已知AB=4,OA=4,求阴影部分的面积.
21.如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB= ,AC= ;
(2)画出在搬动此物体的整个过程中A点所经过的路径,并求出该路径的长度.
(3)设O、H分别为边AB、AC的中点,在将△ABC绕点B顺时针方向翻转到△A1BC1的位置这一过程中,求线段OH所扫过部分的面积.
22.如图,O是的内心,BO的延长线和的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.
求证:≌.
若,求阴影部分的面积.
参考答案
1.B
【解析】分析:根据已知条件得到四边形ABCD是矩形,求得图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD,根据等腰三角形的性质得到∠BAC=∠ABO=36°,由圆周角定理得到∠AOD=72°,于是得到结论.
详解:
:∵AC与BD是⊙O的两条直径, ∴∠ABC=∠ADC=∠DAB=∠BCD=90°, ∴四边形ABCD是矩形, ∴△ABO与△CDO的面积的和=△AOD与△BOC的面积的和, ∴图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD, ∵OA=OB, ∴∠BAC=∠ABO=36°, ∴∠AOD=72°, ∴图中阴影部分的面积=2×=10π.
故选B.
点睛:考查了扇形的面积、矩形的判定和性质和圆周角定理,熟练掌握扇形的面积公式 是解题的关键.
2.D.
【解析】
试题分析:在Rt△ACB中,AB==,∵BC是半圆的直径,∴∠CDB=90°,在等腰Rt△ACB中,CD垂直平分AB,CD=BD=,∴D为半圆的中点,
∴S阴影部分=S扇形ACB﹣S△ADC==.故选D.
考点:扇形面积的计算.
3.B
【解析】
试题分析:不能接触的面积等于边长为2的正方形的面积减去半径为1的圆的面积,即S=4-π.
考点:图形的面积计算
4.A
【解析】
【分析】
如图,弓形①的面积=S扇形ABD-S△ABD,只要求出弓形①的面积,然后乘以4即可.
【详解】
由题意可得,
,
和时等边三角形,
∴弓形①的面积=S扇形ABD-S△ABD=-×22=,
阴影部分的面积为:,
故选:A.
【点睛】
本题考查扇形面积的计算,等边三角形的判定与性质及割补法求图形的面积,解答本题的关键是明确题意,利用数形结合的思想解答.
5.A
【解析】【分析】根据:阴影面积=正方形面积-扇形面积可得. S扇形=.
【详解】S阴影=S正方形-S扇形=22-(cm2)
故选:A
【点睛】本题考核知识点:求扇形面积.解题关键点:求出正方形和扇形面积.
6.B
【解析】分析:先证明△ABE是等边三角形,从而可得∠B=60°,然后根据扇形的弧长计算公式计算即可.
详解: ∵四边形AECD是平行四边形,
∴AE=CD,
∵AB=BE=CD=3,
∴AB=BE=AE,
∴△ABE是等边三角形,
∴∠B=60°,
∴弧AE 的弧长= ,
故选B.
点睛:本题考查了平行四边形的性质、等边三角形的判定和性质、扇形的面积公式,熟练掌握扇形的面积公式是本题的关键,扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=nπR2360或S扇形=12lR(其中l为扇形的弧长).
7.A
【解析】
【分析】
连接OD,则OD⊥AC,△AOD为等腰直角三角形,根据等腰直角三角形性质得到OA=;OD=1,根据△AOD中的阴影面积=S△AOD-S扇形;进而可求阴影总面积.
【详解】
连接OD,则OD⊥AC,△AOD为等腰直角三角形, ∵AB=4,O是AB的中点, ∴OA=;OD=1,
∴△AOD中的阴影面积=×1×1-=-; 则图中阴影部分的面积是1-.
故选:A
【点睛】
本题考核知识点:扇形面积,等腰直角三角形. 解题关键点:掌握等腰直角三角形性质和扇形面积公式.
8.C
【解析】
【分析】
易得AD长,利用相应的三角函数可求得∠ABD的度数,进而求得∠EOD的度数,那么一个阴影部分的面积=S△ABD-S扇形DOE-S△BOE,算出后乘2即可.
【详解】
连接OE,OF. ∵BD=12,AD:AB=1:2, ∴AD=4 ,AB=8,∠ABD=30°, ∴S△ABD=×4×12=24,S扇形=
∵两个阴影的面积相等,
∴阴影面积= .
故选:C
【点睛】
本题主要是理解阴影面积等于三角形面积减扇形面积和三角形面积.
9.B
【解析】
【分析】
先根据正方形的边长,求得,进而得到,再根据,以及扇形的面积公式即可得出图中阴影部分的面积.
【详解】
如图,连结,
,
,
,
,D,在一条直线上,
四边形ABCD是正方形,
,,
,
,
,
,
,
图中阴影部分的面积.
故选B.
【点睛】
本题考查了旋转的性质,正方形性质,勾股定理以及扇形面积的计算等知识点的综合应用,解题关键在于利用旋转前、后的图形全等来进行计算.
10.8﹣2π.
【解析】
【分析】
由半圆的直径为4且与矩形一边BC相切可得矩形的宽AB=2,再根据阴影部分面积=矩形面积﹣半圆面积求解可得.
【详解】
解:∵半圆的直径AD=4,且与BC相切,
∴半径为2,AB=2,
∴图中的阴影部分的面积为4×2﹣?π?22=8﹣2π,
故答案为:8﹣2π.
【点睛】
本题主要考查切线的性质与矩形的性质,解题的关键是掌握矩形的性质、切线的性质及阴影部分面积的计算关系式.
11.
【解析】
【分析】
根据题意可知阴影部分的面积等于扇形OBC的面积与△ODC的面积之差,从而可以解答本题.
【详解】
连接OC,如图所示,
∵在扇形AOB中,∠AOB=90°,,
∴∠AOC=∠COB=45°,
∵四边形CDEF是正方形,OA=,
∴OC=,∠CDO=90°,
∴OD=CD=1,
∴阴影部分的面积是:,
故答案为:.
【点睛】
本题考查扇形面积的计算、正方形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
12.
【解析】
【分析】
分析:由图可知S1=,S2=×3,S3=×5,S4=×7,…Sn=×(2n-1).
【详解】
由图可知S1=,S2=×3,S3=×5=,由题意可得出通项公式:Sn=×(2n-1),即Sn=×(2n-1).
故答案为:(1). (2).
【点睛】
本题是一道规律性的题目,考查了扇形面积的计算,难度较大.
13.
【解析】
【分析】
连接,,根据旋转的性质得到,推出是等边三角形,得到,推出是等边三角形,得到,得到,根据图形的面积公式即可得到答案.
【详解】
连接,,
将半径为2,圆心角为的扇形OAB绕点A逆时针旋转,
,
是等边三角形,
,,
当中上,
,
,
是等边三角形,
,
,
,
,
图中阴影部分的面积,
故答案是:.
【点睛】
考查了扇形面积的计算,等边三角形的判定和性质,旋转的性质,正确的作出辅助线是解题的关键.
14.
【解析】
【分析】
根据题意作出合适的辅助线,可知阴影部分的面积等于扇形DEF的面积与四边形DNCM的面积之差,再根据题目中的数据即可解答本题.
【详解】
连接CD,如右图所示, 在中,,, , 以AB中点D为圆心,作圆心角为的扇形DEF,点C恰好在弧EF上, ,,, , ,, , 在和中, , ≌, 与的面积之和等于与的面积之和, 四边形DNCM的面积等于的面积, 阴影部分的面积是:, 故答案为:.
【点睛】
本题考查扇形面积的计算、等腰直角三角形,解答本题的关键是明确题意,利用数形结合的思想解答.
15.8﹣2π
【解析】
【分析】
根据S阴=S△ABD-S扇形BAE计算即可;
【详解】
S阴=S△ABD-S扇形BAE=×4×4-=8-2π,
故答案为8-2π.
【点睛】
本题考查扇形的面积的计算,正方形的性质等知识,解题的关键是学会用分割法求阴影部分面积.
16.
【解析】分析:过O′作O′M⊥OA于M,解直角三角形求出旋转角的度数,根据图形得出阴影部分的面积S=S扇形OAO′+S△O′AC′-S△OAC-S扇形CAC′=S扇形OAO′-S扇形CAC′,分别求出即可.
详解:过O′作O′M⊥OA于M,则∠O′MA=90°,
∵点O′的坐标是(1,),
∴O′M=,OM=1,
∵AO=2,
∴AM=2-1=1,
∴tan∠O′AM=,
∴∠O′AM=60°,
即旋转角为60°,
∴∠CAC′=∠OAO′=60°,
∵把△OAC绕点A按顺时针方向旋转到△O′AC′,
∴S△OAC=S△O′AC′,
∴阴影部分的面积S=S扇形OAO′+S△O′AC′-S△OAC-S扇形CAC′=S扇形OAO′-S扇形CAC′
=
=,
故答案为:.
点睛:本题考查了解直角三角形,旋转的性质、扇形的面积计算等知识点,能把求不规则图形的面积转化成求出规则图形的面积是解此题的关键.
17.
【解析】
试题分析:∵AE=BE,∠A=∠B,EM=EN,
∴Rt△MAE≌Rt△NBE,
由勾股定理得,AM=BN==,∵AE:ME=1:2,
∴∠AEM=∠BEN=60°,∴∠MEN=60°,
则阴影部分的面积=S正方形﹣2S△AME﹣S扇形EMN
=1﹣2×AM?AE﹣
=.
考点:正方形的性质;切线的性质;扇形面积的计算.
18.(1)100cm2;(2)227cm2.
【解析】
试题分析:(1)过O作OC⊥AB于C,由垂直定理得出AB=2AC,求出∠A=∠B=30°,推出OA=2OC,求出OC,在Rt△ACO中,由勾股定理求出AC,求出AB,根据三角形的面积公式求出即可;
(2)根据S阴影=S扇形AOB-S△AOB即可得出结论.
试题解析:(1)过O作OC⊥AB于C,
∵OC过O,
∴AB=2AC,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∴OA=2OC,
∴OC=10cm,
在Rt△ACO中,由勾股定理得:AC2+OC2=OA2,
即AC2+102=202,
AC=10,
∴AB=2AC=20,
∴S△AOB=×AB×OC=×20×10=100cm2;
(2)S阴影=S扇形AOB-S△AOB
=-100
=-100
≈×3-100×1.73
=400-173
=227cm2.
考点:1.垂径定理;2.勾股定理;4.扇形面积的计算.
19.(1)证明见解析;(2)8+4π.
【解析】
试题分析:(1)利用圆周角定以及等腰三角形的性质得出即可;
(2)首先得出∠BOE=90°,BO=EO=4,∠AOE=90°,进而求出S阴=S△BOE+S扇形OAE的值.
试题解析:(1)连结AD,
∵AB为⊙O直径,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD;
(2)连结OE,
∵AB=8,∠BAC=45°,
∴∠BOE=90°,BO=EO=4,∠AOE=90°,
∴S阴=S△BOE+S扇形OAE=8+4π.
考点:1.扇形面积的计算;2.等腰三角形的性质;3.圆周角定理.
20.(1)证明见解析;(2)S阴=2π.
【解析】
【分析】
(1)根据切线性质和等弧对等角性质可证△AOC≌△BOC(ASA).得AO=BO.(2)先求圆的半径,根据S阴=S△BOC- S扇COE可得.
【详解】
(1)证明:连接OC,则OC⊥AB.
∵=,
∴∠AOC=∠BOC.
在△AOC和△BOC中,
∴△AOC≌△BOC(ASA).
∴AO=BO.
(2)由(1)可得AC=BC=AB=2,
在Rt△AOC中,OC=2,
∴∠AOC=∠BOC=60°.
∴S△BOC=BC·OC=×2×2=2,S扇COE==π.
∴S阴=2-π.
【点睛】
本题考核知识点:切线,扇形面积. 解题关键点:熟记切线性质和扇形面积公式.
21.(1)2米,米
【解析】
试题分析:(1)根据直角三角形的三边关系,30°的角所对的直角边是斜边的一半,可以直接确定AB、AC.
(2)根据要求画出路径,再用弧长公式求解路径的长度.
(3)OH扫过的面积=扇形BHH′的面积﹣扇形BOO′的面积,由此即可计算.
试题解析:(1)∵∠CAB=30°,BC=1米
∴AB=2米,AC=米.
故答案为2米,米.
(2)A点经过的路径如图1中所示,
∵∠ABA1=180°﹣60°=120°,A1A2=AC=米
∴A点所经过的路径长=?π?2+=π+≈5.9(米).
(3)如图2中,
由题意△BOH≌△BO′H′,
∴OH扫过的面积=扇形BHH′的面积﹣扇形BOO′的面积=﹣=π.
考点:轨迹;勾股定理;三角形中位线定理;作图—基本作图;作图-平移变换.
22.(1)证明见解析(2)
【解析】
【分析】
由点O为三角形的内心,得到BO与CO都为角平分线,再由四边形AOCD为平行四边形,得到对边平行且相等,进而利用AAS得到三角形全等;
由三角形全等得到对应边相等,对应角相等,确定出三角形ABC为等边三角形,可得出内心与外心重合,即,阴影部分面积等于扇形AOB面积减去三角形AOB面积,求出即可.
【详解】
是的内心,
,,
,
,
由,,
,
在和中,
,
≌;
由得,,,
,
,
是等边三角形,
是的内心也是外心,
,
设E为BD与AC的交点,BE垂直平分AC,
在中,,,
,
,
.
【点睛】
此题考查了三角形内心与外心,全等三角形的判定与性质,平行四边形的性质,扇形面积的计算,熟练掌握各自的性质是解本题的关键.
姓名:___________班级:___________考号:___________
一、选择题
1.右图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
A. 5πcm2 B. 10πcm2 C. 15πcm2 D. 20πcm2
2.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
A. B. C. D.
3.如图,一张半径为1的圆形纸片在边长为的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
A. B. C. D.
4.如图,线段,分别以A、B为圆心,以AB的长为半径作弧,两弧交于C、D两点,则阴影部分的面积为
A. B. C. D.
5.(题文)如图,正方形ABCD的边长为2cm,以点B为圆心,AB的长为半径作弧AC,则图中阴影部分的面积为( )
A. (4-π)cm2 B. (8-π)cm2 C. (2π-4)cm2 D. (π-2)cm2
6.如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=3,则弧AE 的弧长为( )
A. π B. π C. π D. 3
7.如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )
A. 1﹣π B. 1﹣π C. 2﹣π D. 2﹣π
8.如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为( )
A. 12 B. π C. D. π
9.如图,边长为1的正方形ABCD绕点A逆时针旋转后得到正方形,边与CD交于点O,则图中阴影部分的面积是
A. B. C. D.
二、填空题
10.如图,在矩形ABCD中,以AD为直径的半圆与边BC相切于点E,若AD=4,则图中的阴影部分的面积为 .
11.如图,在扇形AOB中,,,过点C作于点D,以CD为边向右作正方形CDEF,若,则阴影部分的面积是______结果保留.
12.如图是圆心角为 30°,半径分别是 1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为 S1、
S2、S3、…,则 S3=__________,Sn=__________.结果保留 π)
13.如图,将半径为2,圆心角为的扇形OAB绕点A逆时针旋转,点O,B的对应点分别为,,连接,则图中阴影部分的面积是______.
14.如图,在中,,,以AB中点D为圆心,作圆心角为的扇形DEF,点C恰好在弧EF上,则图中阴影部分面积为______.
15.如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是_____(结果保留π)
16.如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
三、解答题
17.如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是 .
18.如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120o.求:
(1)△OAB的面积.
(2)阴影部分的面积.(精确到1cm2)
19.如图,AB为的直径,AB=AC,BC交于点D,AC交于点E.
(1)求证:BD=CD;
(2)若AB=8,∠BAC=45°,求阴影部分的面积.
20.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,.
(1)求证:OA=OB;
(2)已知AB=4,OA=4,求阴影部分的面积.
21.如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB= ,AC= ;
(2)画出在搬动此物体的整个过程中A点所经过的路径,并求出该路径的长度.
(3)设O、H分别为边AB、AC的中点,在将△ABC绕点B顺时针方向翻转到△A1BC1的位置这一过程中,求线段OH所扫过部分的面积.
22.如图,O是的内心,BO的延长线和的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.
求证:≌.
若,求阴影部分的面积.
参考答案
1.B
【解析】分析:根据已知条件得到四边形ABCD是矩形,求得图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD,根据等腰三角形的性质得到∠BAC=∠ABO=36°,由圆周角定理得到∠AOD=72°,于是得到结论.
详解:
:∵AC与BD是⊙O的两条直径, ∴∠ABC=∠ADC=∠DAB=∠BCD=90°, ∴四边形ABCD是矩形, ∴△ABO与△CDO的面积的和=△AOD与△BOC的面积的和, ∴图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD, ∵OA=OB, ∴∠BAC=∠ABO=36°, ∴∠AOD=72°, ∴图中阴影部分的面积=2×=10π.
故选B.
点睛:考查了扇形的面积、矩形的判定和性质和圆周角定理,熟练掌握扇形的面积公式 是解题的关键.
2.D.
【解析】
试题分析:在Rt△ACB中,AB==,∵BC是半圆的直径,∴∠CDB=90°,在等腰Rt△ACB中,CD垂直平分AB,CD=BD=,∴D为半圆的中点,
∴S阴影部分=S扇形ACB﹣S△ADC==.故选D.
考点:扇形面积的计算.
3.B
【解析】
试题分析:不能接触的面积等于边长为2的正方形的面积减去半径为1的圆的面积,即S=4-π.
考点:图形的面积计算
4.A
【解析】
【分析】
如图,弓形①的面积=S扇形ABD-S△ABD,只要求出弓形①的面积,然后乘以4即可.
【详解】
由题意可得,
,
和时等边三角形,
∴弓形①的面积=S扇形ABD-S△ABD=-×22=,
阴影部分的面积为:,
故选:A.
【点睛】
本题考查扇形面积的计算,等边三角形的判定与性质及割补法求图形的面积,解答本题的关键是明确题意,利用数形结合的思想解答.
5.A
【解析】【分析】根据:阴影面积=正方形面积-扇形面积可得. S扇形=.
【详解】S阴影=S正方形-S扇形=22-(cm2)
故选:A
【点睛】本题考核知识点:求扇形面积.解题关键点:求出正方形和扇形面积.
6.B
【解析】分析:先证明△ABE是等边三角形,从而可得∠B=60°,然后根据扇形的弧长计算公式计算即可.
详解: ∵四边形AECD是平行四边形,
∴AE=CD,
∵AB=BE=CD=3,
∴AB=BE=AE,
∴△ABE是等边三角形,
∴∠B=60°,
∴弧AE 的弧长= ,
故选B.
点睛:本题考查了平行四边形的性质、等边三角形的判定和性质、扇形的面积公式,熟练掌握扇形的面积公式是本题的关键,扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=nπR2360或S扇形=12lR(其中l为扇形的弧长).
7.A
【解析】
【分析】
连接OD,则OD⊥AC,△AOD为等腰直角三角形,根据等腰直角三角形性质得到OA=;OD=1,根据△AOD中的阴影面积=S△AOD-S扇形;进而可求阴影总面积.
【详解】
连接OD,则OD⊥AC,△AOD为等腰直角三角形, ∵AB=4,O是AB的中点, ∴OA=;OD=1,
∴△AOD中的阴影面积=×1×1-=-; 则图中阴影部分的面积是1-.
故选:A
【点睛】
本题考核知识点:扇形面积,等腰直角三角形. 解题关键点:掌握等腰直角三角形性质和扇形面积公式.
8.C
【解析】
【分析】
易得AD长,利用相应的三角函数可求得∠ABD的度数,进而求得∠EOD的度数,那么一个阴影部分的面积=S△ABD-S扇形DOE-S△BOE,算出后乘2即可.
【详解】
连接OE,OF. ∵BD=12,AD:AB=1:2, ∴AD=4 ,AB=8,∠ABD=30°, ∴S△ABD=×4×12=24,S扇形=
∵两个阴影的面积相等,
∴阴影面积= .
故选:C
【点睛】
本题主要是理解阴影面积等于三角形面积减扇形面积和三角形面积.
9.B
【解析】
【分析】
先根据正方形的边长,求得,进而得到,再根据,以及扇形的面积公式即可得出图中阴影部分的面积.
【详解】
如图,连结,
,
,
,
,D,在一条直线上,
四边形ABCD是正方形,
,,
,
,
,
,
,
图中阴影部分的面积.
故选B.
【点睛】
本题考查了旋转的性质,正方形性质,勾股定理以及扇形面积的计算等知识点的综合应用,解题关键在于利用旋转前、后的图形全等来进行计算.
10.8﹣2π.
【解析】
【分析】
由半圆的直径为4且与矩形一边BC相切可得矩形的宽AB=2,再根据阴影部分面积=矩形面积﹣半圆面积求解可得.
【详解】
解:∵半圆的直径AD=4,且与BC相切,
∴半径为2,AB=2,
∴图中的阴影部分的面积为4×2﹣?π?22=8﹣2π,
故答案为:8﹣2π.
【点睛】
本题主要考查切线的性质与矩形的性质,解题的关键是掌握矩形的性质、切线的性质及阴影部分面积的计算关系式.
11.
【解析】
【分析】
根据题意可知阴影部分的面积等于扇形OBC的面积与△ODC的面积之差,从而可以解答本题.
【详解】
连接OC,如图所示,
∵在扇形AOB中,∠AOB=90°,,
∴∠AOC=∠COB=45°,
∵四边形CDEF是正方形,OA=,
∴OC=,∠CDO=90°,
∴OD=CD=1,
∴阴影部分的面积是:,
故答案为:.
【点睛】
本题考查扇形面积的计算、正方形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
12.
【解析】
【分析】
分析:由图可知S1=,S2=×3,S3=×5,S4=×7,…Sn=×(2n-1).
【详解】
由图可知S1=,S2=×3,S3=×5=,由题意可得出通项公式:Sn=×(2n-1),即Sn=×(2n-1).
故答案为:(1). (2).
【点睛】
本题是一道规律性的题目,考查了扇形面积的计算,难度较大.
13.
【解析】
【分析】
连接,,根据旋转的性质得到,推出是等边三角形,得到,推出是等边三角形,得到,得到,根据图形的面积公式即可得到答案.
【详解】
连接,,
将半径为2,圆心角为的扇形OAB绕点A逆时针旋转,
,
是等边三角形,
,,
当中上,
,
,
是等边三角形,
,
,
,
,
图中阴影部分的面积,
故答案是:.
【点睛】
考查了扇形面积的计算,等边三角形的判定和性质,旋转的性质,正确的作出辅助线是解题的关键.
14.
【解析】
【分析】
根据题意作出合适的辅助线,可知阴影部分的面积等于扇形DEF的面积与四边形DNCM的面积之差,再根据题目中的数据即可解答本题.
【详解】
连接CD,如右图所示, 在中,,, , 以AB中点D为圆心,作圆心角为的扇形DEF,点C恰好在弧EF上, ,,, , ,, , 在和中, , ≌, 与的面积之和等于与的面积之和, 四边形DNCM的面积等于的面积, 阴影部分的面积是:, 故答案为:.
【点睛】
本题考查扇形面积的计算、等腰直角三角形,解答本题的关键是明确题意,利用数形结合的思想解答.
15.8﹣2π
【解析】
【分析】
根据S阴=S△ABD-S扇形BAE计算即可;
【详解】
S阴=S△ABD-S扇形BAE=×4×4-=8-2π,
故答案为8-2π.
【点睛】
本题考查扇形的面积的计算,正方形的性质等知识,解题的关键是学会用分割法求阴影部分面积.
16.
【解析】分析:过O′作O′M⊥OA于M,解直角三角形求出旋转角的度数,根据图形得出阴影部分的面积S=S扇形OAO′+S△O′AC′-S△OAC-S扇形CAC′=S扇形OAO′-S扇形CAC′,分别求出即可.
详解:过O′作O′M⊥OA于M,则∠O′MA=90°,
∵点O′的坐标是(1,),
∴O′M=,OM=1,
∵AO=2,
∴AM=2-1=1,
∴tan∠O′AM=,
∴∠O′AM=60°,
即旋转角为60°,
∴∠CAC′=∠OAO′=60°,
∵把△OAC绕点A按顺时针方向旋转到△O′AC′,
∴S△OAC=S△O′AC′,
∴阴影部分的面积S=S扇形OAO′+S△O′AC′-S△OAC-S扇形CAC′=S扇形OAO′-S扇形CAC′
=
=,
故答案为:.
点睛:本题考查了解直角三角形,旋转的性质、扇形的面积计算等知识点,能把求不规则图形的面积转化成求出规则图形的面积是解此题的关键.
17.
【解析】
试题分析:∵AE=BE,∠A=∠B,EM=EN,
∴Rt△MAE≌Rt△NBE,
由勾股定理得,AM=BN==,∵AE:ME=1:2,
∴∠AEM=∠BEN=60°,∴∠MEN=60°,
则阴影部分的面积=S正方形﹣2S△AME﹣S扇形EMN
=1﹣2×AM?AE﹣
=.
考点:正方形的性质;切线的性质;扇形面积的计算.
18.(1)100cm2;(2)227cm2.
【解析】
试题分析:(1)过O作OC⊥AB于C,由垂直定理得出AB=2AC,求出∠A=∠B=30°,推出OA=2OC,求出OC,在Rt△ACO中,由勾股定理求出AC,求出AB,根据三角形的面积公式求出即可;
(2)根据S阴影=S扇形AOB-S△AOB即可得出结论.
试题解析:(1)过O作OC⊥AB于C,
∵OC过O,
∴AB=2AC,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∴OA=2OC,
∴OC=10cm,
在Rt△ACO中,由勾股定理得:AC2+OC2=OA2,
即AC2+102=202,
AC=10,
∴AB=2AC=20,
∴S△AOB=×AB×OC=×20×10=100cm2;
(2)S阴影=S扇形AOB-S△AOB
=-100
=-100
≈×3-100×1.73
=400-173
=227cm2.
考点:1.垂径定理;2.勾股定理;4.扇形面积的计算.
19.(1)证明见解析;(2)8+4π.
【解析】
试题分析:(1)利用圆周角定以及等腰三角形的性质得出即可;
(2)首先得出∠BOE=90°,BO=EO=4,∠AOE=90°,进而求出S阴=S△BOE+S扇形OAE的值.
试题解析:(1)连结AD,
∵AB为⊙O直径,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD;
(2)连结OE,
∵AB=8,∠BAC=45°,
∴∠BOE=90°,BO=EO=4,∠AOE=90°,
∴S阴=S△BOE+S扇形OAE=8+4π.
考点:1.扇形面积的计算;2.等腰三角形的性质;3.圆周角定理.
20.(1)证明见解析;(2)S阴=2π.
【解析】
【分析】
(1)根据切线性质和等弧对等角性质可证△AOC≌△BOC(ASA).得AO=BO.(2)先求圆的半径,根据S阴=S△BOC- S扇COE可得.
【详解】
(1)证明:连接OC,则OC⊥AB.
∵=,
∴∠AOC=∠BOC.
在△AOC和△BOC中,
∴△AOC≌△BOC(ASA).
∴AO=BO.
(2)由(1)可得AC=BC=AB=2,
在Rt△AOC中,OC=2,
∴∠AOC=∠BOC=60°.
∴S△BOC=BC·OC=×2×2=2,S扇COE==π.
∴S阴=2-π.
【点睛】
本题考核知识点:切线,扇形面积. 解题关键点:熟记切线性质和扇形面积公式.
21.(1)2米,米
【解析】
试题分析:(1)根据直角三角形的三边关系,30°的角所对的直角边是斜边的一半,可以直接确定AB、AC.
(2)根据要求画出路径,再用弧长公式求解路径的长度.
(3)OH扫过的面积=扇形BHH′的面积﹣扇形BOO′的面积,由此即可计算.
试题解析:(1)∵∠CAB=30°,BC=1米
∴AB=2米,AC=米.
故答案为2米,米.
(2)A点经过的路径如图1中所示,
∵∠ABA1=180°﹣60°=120°,A1A2=AC=米
∴A点所经过的路径长=?π?2+=π+≈5.9(米).
(3)如图2中,
由题意△BOH≌△BO′H′,
∴OH扫过的面积=扇形BHH′的面积﹣扇形BOO′的面积=﹣=π.
考点:轨迹;勾股定理;三角形中位线定理;作图—基本作图;作图-平移变换.
22.(1)证明见解析(2)
【解析】
【分析】
由点O为三角形的内心,得到BO与CO都为角平分线,再由四边形AOCD为平行四边形,得到对边平行且相等,进而利用AAS得到三角形全等;
由三角形全等得到对应边相等,对应角相等,确定出三角形ABC为等边三角形,可得出内心与外心重合,即,阴影部分面积等于扇形AOB面积减去三角形AOB面积,求出即可.
【详解】
是的内心,
,,
,
,
由,,
,
在和中,
,
≌;
由得,,,
,
,
是等边三角形,
是的内心也是外心,
,
设E为BD与AC的交点,BE垂直平分AC,
在中,,,
,
,
.
【点睛】
此题考查了三角形内心与外心,全等三角形的判定与性质,平行四边形的性质,扇形面积的计算,熟练掌握各自的性质是解本题的关键.
同课章节目录
