2.1 图形的轴对称同步课时作业

2.1 图形的轴对称同步课时作业
姓名：___________班级：___________考号：___________
一、选择题
1．下面有四个图案，其中不是轴对称图形的是(　 　)
A． B． C． D．
2．如图，将一个矩形纸片ABCD，沿着BE折叠，使C、D两点分别落在点、处若，则的度数为　　
A． B． C． D．
3．下列说法中错误的是（　　）
A． 两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B． 关于某直线对称的两个图形全等
C． 面积相等的两个四边形对称
D． 轴对称指的是两个图形沿着某一条直线对折后能完全重合
4．如图所示的方格纸，已有两个小正方形被涂黑，再将图中其余小正方形涂黑一个，使整个被涂黑的图案构成一个轴对称图形，那么涂法共有（　　）种．
A． 6 B． 5 C． 4 D． 3
5．如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（　　）
A． B． 1 C． D． 2
6．如图，将△ABC沿DE，EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠DOF=142°，则∠C的度数为（　　）
A． 38° B． 39° C． 42° D． 48°
7．如图，在△ABC 中，AB=AC，∠C=70°，△AB′C′与△ABC 关于直线 EF对称，∠CAF=10°，连接 BB′，则∠ABB′的度数是（ ）
A． 30° B． 35° C． 40° D． 45°
8．一张正方形纸片按图中方式经过两次对折，并在如图3位置上剪去一个小正方形，打开后是（　　）
A． B． C． D．
二、填空题
9．角是轴对称图形,它的对称轴是____,线段是轴对称图形,它的对称轴是____.
10．有些字母是轴对称图形，在E，H，I，M，N这5个字母中，是轴对称图形的是__________.
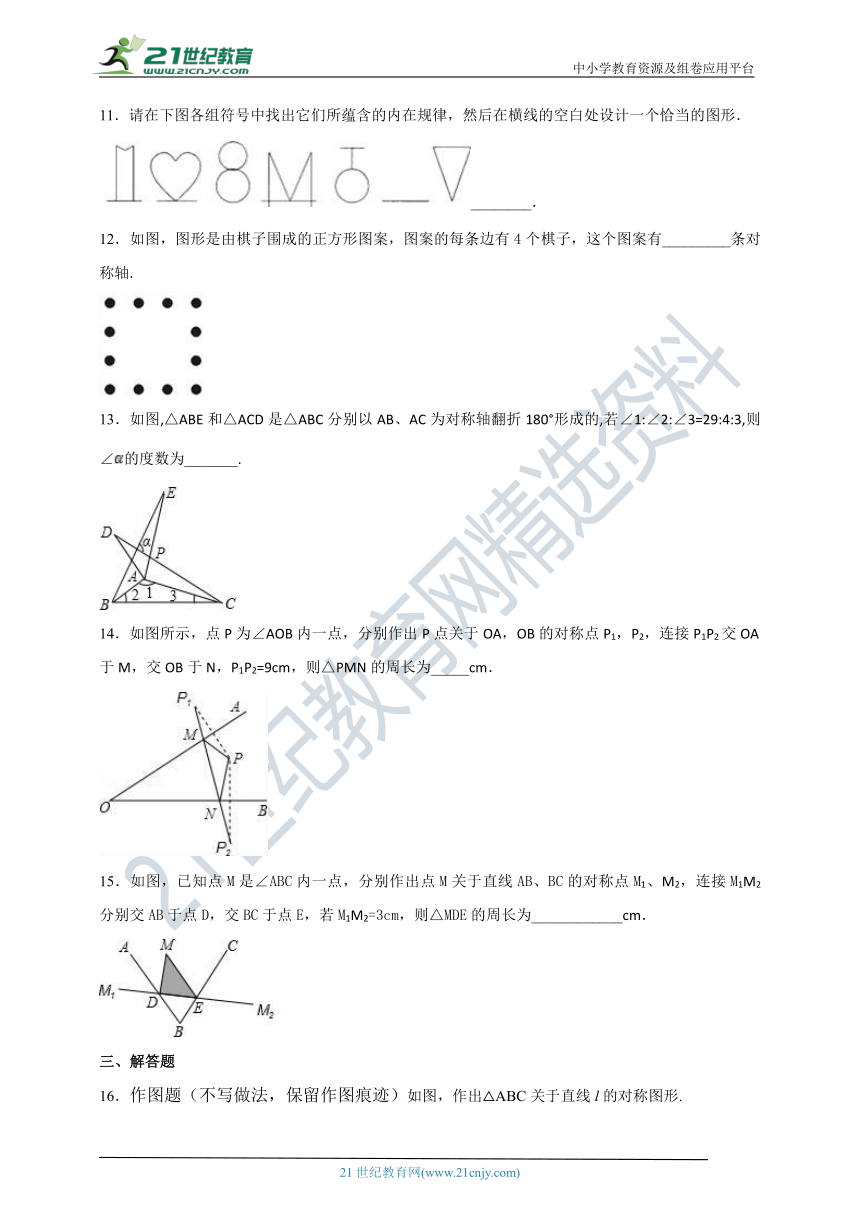
11．请在下图各组符号中找出它们所蕴含的内在规律，然后在横线的空白处设计一个恰当的图形．
________．
12．如图，图形是由棋子围成的正方形图案，图案的每条边有4个棋子，这个图案有_________条对称轴.
13．如图,△ABE和△ACD是△ABC分别以AB、AC为对称轴翻折180°形成的,若∠1:∠2:∠3=29:4:3,则∠的度数为_______.
14．如图所示，点P为∠AOB内一点，分别作出P点关于OA，OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=9cm，则△PMN的周长为_____cm．
15．如图，已知点M是∠ABC内一点，分别作出点M关于直线AB、BC的对称点M1、M2，连接M1M2分别交AB于点D，交BC于点E，若M1M2=3cm，则△MDE的周长为____________cm．
三、解答题
16．作图题（不写做法，保留作图痕迹）如图，作出△ABC关于直线l的对称图形.
17．如图，∠A=90°，E为BC上一点，A点和E点关于BD对称，B点、C点关于DE对称，求∠ABC和∠C的度数．
18．如图所示，在图形中标出点A、B、C关于直线l的对称点D、E、F。若M为AB的中点，在图中标出它的对称点N。若AB=10，AB边上的高为4，则△DEF的面积为多少？
19．已知如图，点P在内，请按要求完成以下问题．
分别作P关于OA、OB的对称点M、N，连结MN分别交OA、OB于E、F；
若的周长为20，求MN的长．
20．如图，在正方形网格中，点A、B、C、M、N都在格点上（不写作法）
(1)作△ABC关于直线MN对称的△A’B’C’：
(2)将△ABC向上平移两个单位得△A1B1C1，画出△A1B1C1；
(3)在直线MN上找一点P，使AP+CP的值最小．
(4)若网格中最小正方形的边长为1，直接写出△ABC的面积．
参考答案
1．A
【解析】
【分析】
定义：如果一个图形沿着一条直线对折后两部分完全重合，那么这样的图形就叫做轴对称图形.
【详解】
根据轴对称图形的定义可知，A选项明显不是轴对称图形.
【点睛】
理解轴对称图形的定义是解题的关键.
2．B
【解析】
【分析】
根据折叠前后对应角相等即可得出答案．
【详解】
设∠ABE=x，根据折叠前后角相等可知，∠C1BE=∠CBE=50°+x，所以50°+x+x=90°，解得x=20°．
故选：B
【点睛】
本题考核知识点：轴对称. 解题关键点：理解折叠的意义.
3．C
【解析】
【分析】
认真阅读各选项提供的已知条件，根据轴对称图形的定义与性质进行逐一验证，答案可得．
【详解】
根据轴对称的性质，两个对称的图形对应点连线的垂直平分线就是它们的对称轴，故A正确；
根据轴对称的性质，关于某直线对称的两个图形全等，故B正确；
根据面积相等的两个四边形不一定全等，故不一定轴对称，故C错误；
根据轴对称的概念，可知轴对称指的是两个图形沿着某一条直线对折后能完全重合，故D正确．故选：C．
【点睛】
本题考查轴对称的性质；如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形．折痕所在的这条直线叫做对称轴．找着每个选项正误的具体原因是正确解答本题的关键．
4．A
【解析】
【分析】
根据轴对称图形的概念，选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，如图：
【详解】
根据轴对称图形的概念，选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，如图：
可以选择的位置有以下几种：1处，2处，3处，4处，5处，6处，选择的位置共有6处．
故选：A
【点睛】
本题考核知识点：轴对称图形. 解题关键点：理解轴对称图形的定义.
5．B
【解析】分析：先作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值．然后证明四边形ABNM′为平行四边形，即可求出MP+NP=M′N=AB=1．
详解：如图
，
作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值，最小值为M′N的长．
∵菱形ABCD关于AC对称，M是AB边上的中点，
∴M′是AD的中点，
又∵N是BC边上的中点，
∴AM′∥BN，AM′=BN，
∴四边形ABNM′是平行四边形，
∴M′N=AB=1，
∴MP+NP=M′N=1，即MP+NP的最小值为1，
故选：B．
点睛：本题考查的是轴对称-最短路线问题及菱形的性质，熟知两点之间线段最短的知识是解答此题的关键．
6．A
【解析】
分析：根据翻折的性质得出∠A=∠DOE，∠B=∠FOE，进而得出∠DOF=∠A+∠B，利用三角形内角和解答即可．
详解：∵将△ABC沿DE，EF翻折，∴∠A=∠DOE，∠B=∠FOE，∴∠DOF=∠DOE+∠EOF=∠A+∠B=142°，∴∠C=180°﹣∠A﹣∠B=180°﹣142°=38°．
故选A．
点睛：本题考查了三角形内角和定理、翻折的性质等知识，解题的关键是灵活运用这些知识解决问题，学会把条件转化的思想，属于中考常考题型．
7．C
【解析】
【分析】
由轴对称图形的性质可得△BAC≌△B′AC′，进而结合三角形内角和定理即可得出答案．
【详解】
如图，连接 BB′
∵△AB′C′与△ABC 关于直线 EF 对称，
∴△BAC≌△B′AC′，
∵AB=AC，∠C=70°，
∴∠ABC=∠AC′B′=∠AB′C′=70°，
∴∠BAC=∠B′AC′=40°，
∵∠CAF=10°，
∴∠C′AF=10°，
∴∠BAB′=40°+10°+10°+40°=100°，
∴∠ABB′=∠AB′B=40°，
故选C．
【点睛】
本题考查了轴对称图形的性质以及等腰三角形的性质，正确得出∠BAC的度数是解题关键．
8．D
【解析】
【分析】
由平面图形的折叠及图形的对称性展开图解题．
【详解】
动手操作或由图形的对称性，因剪去的小正方形紧靠对折线，可得打开后是D．
故选D．
【点睛】
本题主要考查了剪纸问题，关键是根据折叠方法亲手做一做，这样可以直观的得到答案．
9． 角平分线所在的直线 线段的垂直平分线和线段自身所在的直线
【解析】
【分析】
根据轴对称图形的概念求解．
【详解】
角是轴对称图形，它的对称轴是：角的平分线所在直线．线段是轴对称图形，它的对称轴是：线段的垂直平分线或线段本身所在的直线；
故答案是：线段的垂直平分线或线段本身所在的直线；角的平分线所在直线．
【点睛】
考查轴对称图形的概念，注意掌握轴对称的关键是寻找对称轴，两边图象折叠后可重合．
10．E，H，I，M
【解析】试题解析：根据轴对称图形的定义，可知都是轴对称图形.
故答案为：
点睛：若存在沿某条直线折叠可使左右重合，则其是轴对称图形，否则不是.
11．
【解析】试题解析：从图中可以发现所有的图形都是轴对称图形，而且图形从左到右分别是1?7的数字，
所以画一个轴对称图形且数字为6即可.
故答案为：
12．4
【解析】解：作为一个正方形，其对称轴只有四条．故答案为：4．
13．70°
【解析】
【分析】
根据轴对称的性质可得∠ACB=∠ACD，∠ABC=∠EBA，再根据三角形的内角和等于180°列式计算即可∠2+∠3的度数，然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠α．
【详解】
解：由题可得，∠ACB=∠ACD，∠ABC=∠EBA，
∵∠1：∠2：∠3=29：4：3，
∴∠2+∠3=180°×=35°，
∴∠α=∠EBC+∠DCB=2（∠2+∠3）=2×35°=70°，
故答案为：70°．
【点睛】
本题考查轴对称的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，三角形的内角和定理，熟记性质并表示出∠α是解题的关键．
14．9
【解析】
【分析】
P点关于OA的对称是点P1,P点关于OB的对称点P2,故有PM=P1M,PN=P2N,继而可得: △PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2.
【详解】
∵P点关于OA的对称是点P1,P点关于OB的对称点P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=9,
故答案为:9.
【点睛】
本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等．
15．3
【解析】分析：根据对称轴的意义，可以求出EM=EM2，DM1=DM，M1M2=3cm，可以求出△MDE的周长．
详解：∵点M关于直线AB，BC的对称点M1，M2，∴EM=EM2，DM1=DM，∴△MDE的周长=DE+EM+DM=M1M2=3（cm），∴△MDE的周长=3cm．
故答案为：3．
点睛：本题考查了轴对称的性质与运用，对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．
16．作图见解析.
【解析】分析：分别作出点A、B、C关于直线l的对称点A′、B′、C′，然后顺次连接即可．
详解：△ABC关于直线l的对称图形△A′B′C′如图所示．
点睛：本题考查了轴对称的知识点，熟练掌握轴对称点的作法是解题的关键．
17．∠ABC =60°，∠C=30°．
【解析】试题分析：根据轴对称的性质，可知图中有两组全等的三角形，再由全等三角形的对应角相等，可知，再根据三角形内角和定理即可求得所求角的度数.
试题解析：
∵A点和E点关于BD对称，
∴∠ABD=∠EBD，即∠ABC=2∠ABD=2∠EBD．
又B点、C点关于DE对称，
∴∠DBE=∠C，∠ABC=2∠C．
∵∠A=90°，∴∠ABC+∠C=2∠C+∠C=3∠C=90°．
∴∠C=30°，
∴∠ABC=2∠C=60°．
18．△DEF的面积是20
【解析】试题分析：根据轴对称的性质，可知两个三角形全等，所以对应边相等，再由题中给出条件易得所求三角形的面积.
试题解析：如图所示，
∵AB=10，∴DE=AB=10，
∴.
答：△DEF的面积是20．
19．(1)见解析;(2)20cm.
【解析】
【分析】
(1)根据轴对称的特点画出对应点，并连线；（2）根据轴对称性质可知：，，的周长.
【详解】
解：如图所示： 点P与点M关于AO对称，点P与点N关于BO对称，，，的周长，．
【点睛】
本题考核知识点：轴对称.解题关键点：理解轴对称的性质.
20．(1)作图见解析；（2）作图见解析；（）作图见解析；（4）3.
【解析】
【分析】
（1）首先确定A、B、C三点关于MN对称的对称点位置，再连接即可.
（2）首先确定A1、B1、C1三点，再连接即可.
（3）连结AC′或CA′与MN交于点P，则点P为所找的点.
（4）利用三角形AB为底边，再确定高，即可求出面积．
【详解】
（1）如图，△A′B′C′为所作的图形.
（2）如图，△A1B1C1为所画的图形.
（3）连结AC′或CA′与MN交于点P，则点P为所找的点.
（4） ×3×2=3.
【点睛】
此题主要考查了作图--轴对称变换，几何图形都可看做是有点组成，我们在画一个图形的轴对称图形时，也就是确定一些特殊点的对称点．