2.6 直角三角形同步课时作业（1）

2.6 直角三角形同步课时作业（1）
姓名：___________班级：___________考号：___________
一、选择题
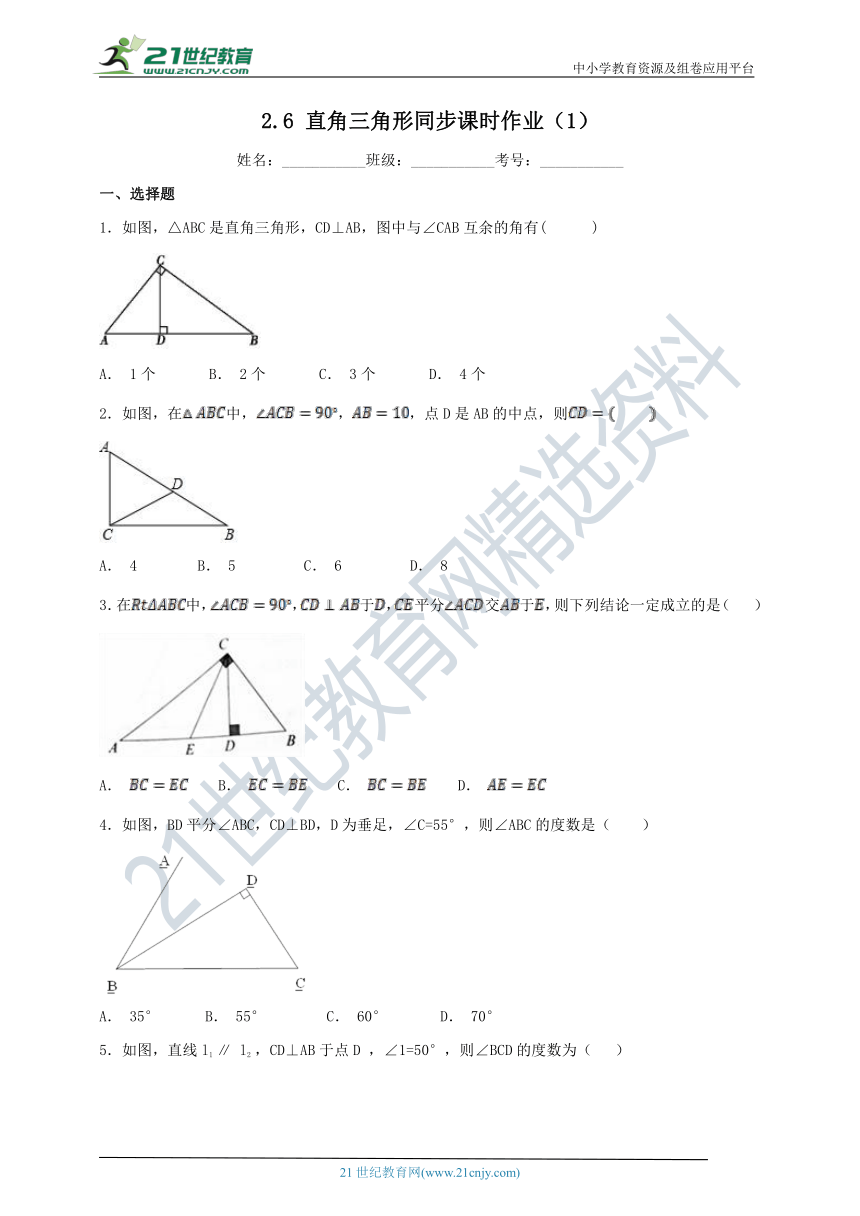
1．如图，△ABC是直角三角形，CD⊥AB，图中与∠CAB互余的角有(　 　)
A． 1个 B． 2个 C． 3个 D． 4个
2．如图，在中，，，点D是AB的中点，则　　
A． 4 B． 5 C． 6 D． 8
3．在中，，于，平分交于，则下列结论一定成立的是（ ）
A． B． C． D．
4．如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是（　　）
A． 35° B． 55° C． 60° D． 70°
5．如图，直线l1 ∥ l2 ，CD⊥AB于点D ，∠1=50°，则∠BCD的度数为（ ）
A． 40° B． 45° C． 50° D． 30°
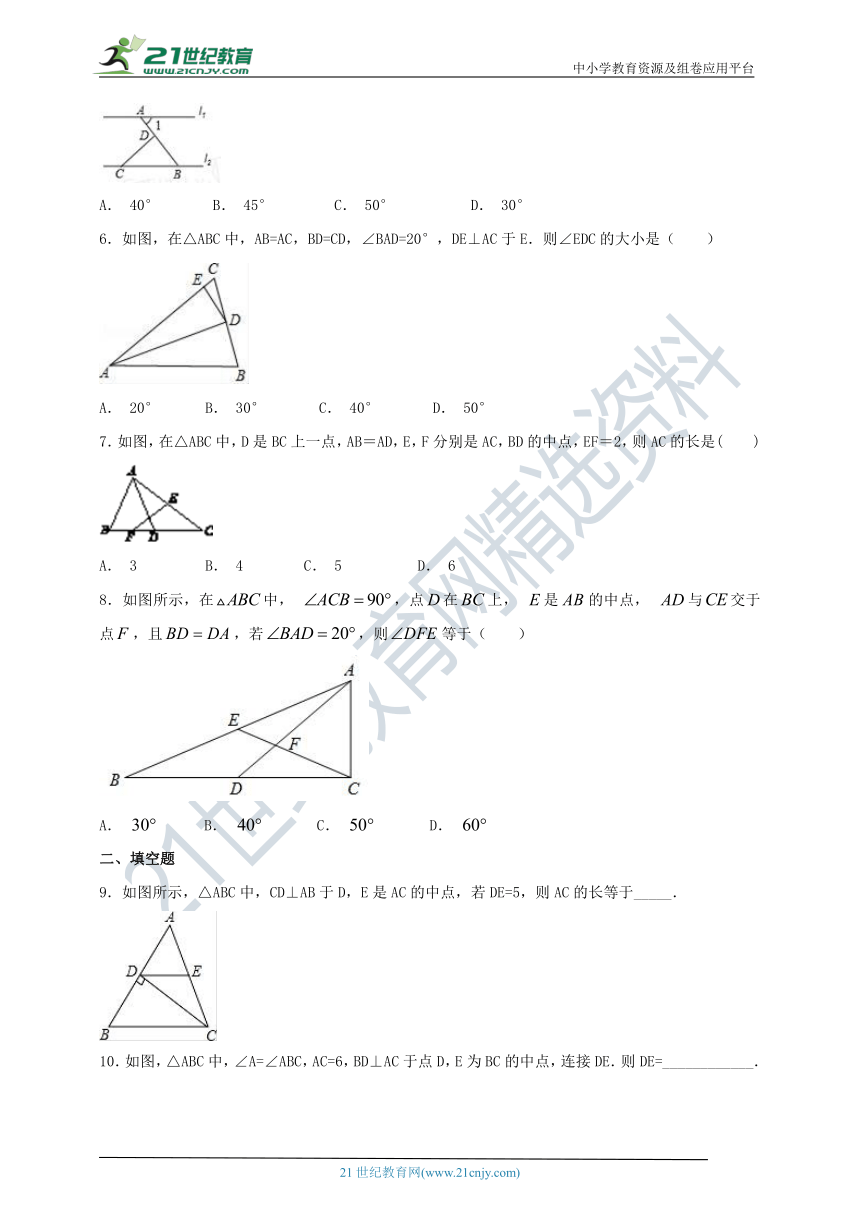
6．如图，在△ABC中，AB=AC，BD=CD，∠BAD=20°，DE⊥AC于E．则∠EDC的大小是（　　）
A． 20° B． 30° C． 40° D． 50°
7．如图，在△ABC中，D是BC上一点，AB＝AD，E，F分别是AC，BD的中点，EF＝2，则AC的长是(　　)
A． 3 B． 4 C． 5 D． 6
8．如图所示，在中， ，点在上， 是的中点， 与交于点，且，若，则等于（　　）
A． B． C． D．
二、填空题
9．如图所示，△ABC中，CD⊥AB于D，E是AC的中点，若DE=5，则AC的长等于_____．
10．如图，△ABC中，∠A=∠ABC，AC=6，BD⊥AC于点D，E为BC的中点，连接DE．则DE=____________．
11．在Rt△ABC中，∠ACB＝90°，CA＝CB，如果斜边AB＝10cm，那么斜边上的高CD＝_______cm．
12．在中，，比大则______．
13．如图，△ABC中，∠B=∠C，FD⊥BC于D，DE⊥AB于E，∠AFD=158°，则∠EDF等于_____度．
14．14．如图，在△ABC中，AB=AC，BC=6，AF⊥BC于点F，BE⊥AC于点E，且点D是AB的中点，△DEF的周长是11，则AB=______．
三、解答题
15．如图，在Rt△ABC中，∠BAC=90°，AD是BC边上的中线，ED⊥BC于D，交BA延长线于点E，若∠E=35°，求∠BDA的度数．
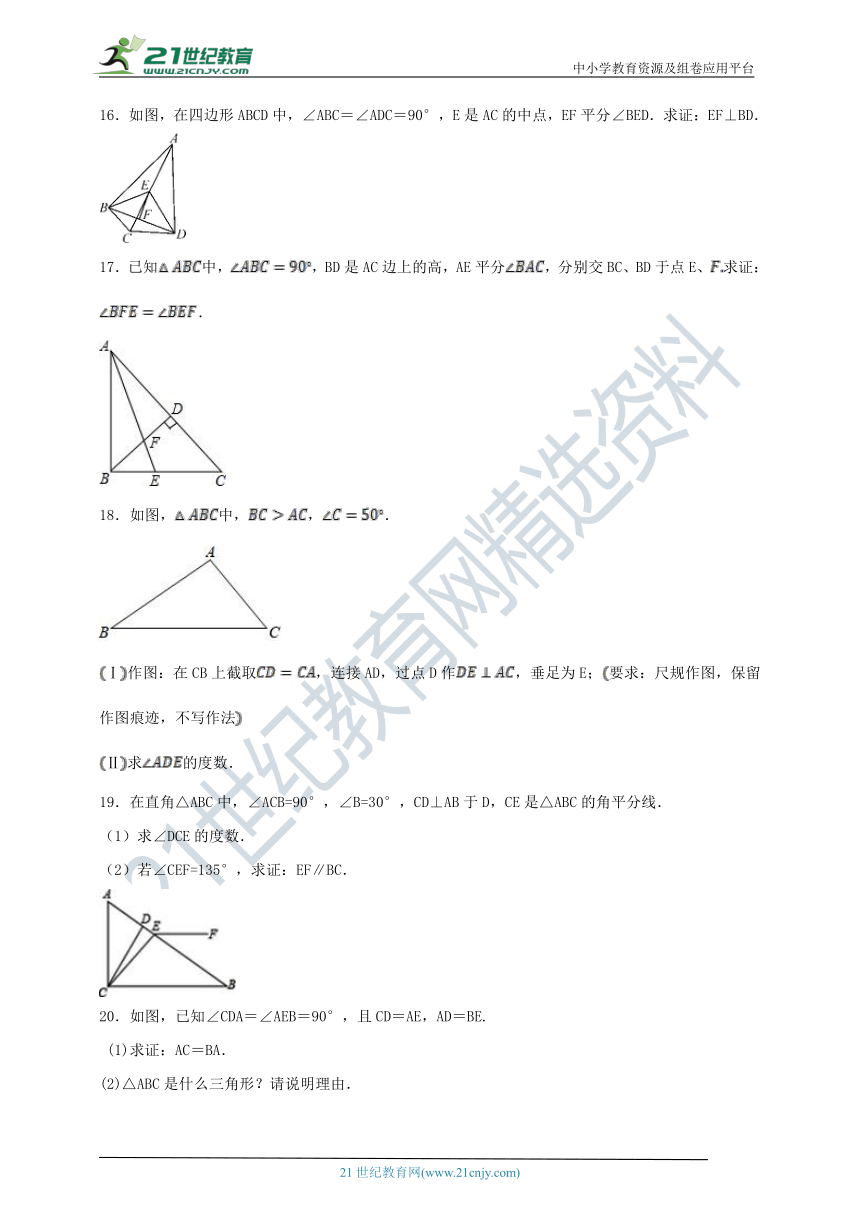
16．如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，E是AC的中点，EF平分∠BED．求证：EF⊥BD．
17．已知中，，BD是AC边上的高，AE平分，分别交BC、BD于点E、求证：．
18．如图，中，，．
Ⅰ作图：在CB上截取，连接AD，过点D作，垂足为E；要求：尺规作图，保留作图痕迹，不写作法
Ⅱ求的度数．
19．在直角△ABC中，∠ACB=90°，∠B=30°，CD⊥AB于D，CE是△ABC的角平分线．
（1）求∠DCE的度数．
（2）若∠CEF=135°，求证：EF∥BC．
20．如图，已知∠CDA＝∠AEB＝90°，且CD＝AE，AD＝BE.
(1)求证：AC＝BA．
(2)△ABC是什么三角形？请说明理由．
(3)如果AM⊥BC，那么AM＝BC吗？请说明理由．
21．如图①，在△ABC中，AE平分∠BAC，∠C＞∠B，F是AE上一点，且FD⊥BC于D点．
(1)试猜想∠EFD，∠B，∠C的关系，并说明理由；
(2)如图②，当点F在AE的延长线上时，其余条件不变，(1)中的结论还成立吗？说明理由．
①　　　　　　　　②
参考答案
1．B
【解析】分析: 根据互余的两个角的和等于90°写出与∠A的和等于90°的角即可．
详解: ∵CD是Rt△ABC斜边上的高，
∴∠A+∠B=90°，∠A+∠ACD=90°，
∴与∠A互余的角有∠B和∠ACD共2个．
故选B．
点睛:本题考查了余角的定义及数形结合的数学思想，熟练掌握互余的两个角的和等于90°是解答本题的关键.
2．B
【解析】
【分析】
根据直角三角形中，斜边上的中线等于斜边的一半解答即可．
【详解】
，点D为AB的中点，
．
故选：B．
【点睛】
本题考查直角三角形的性质，掌握在直角三角形中斜边上的中线等于斜边的一半是解题的关键．
3．C
【解析】分析：根据同角的余角相等可得出∠BCD=∠A，根据角平分线的定义可得出∠ACE=∠DCE，再结合∠BEC=∠A+∠ACE、∠BCE=∠BCD+∠DCE即可得出∠BEC=∠BCE，利用等角对等边即可得出BC=BE，此题得解．
详解：∵∠ACB=90°，CD⊥AB，
∴∠ACD+∠BCD=90°，∠ACD+∠A=90°，
∴∠BCD=∠A．
∵CE平分∠ACD，
∴∠ACE=∠DCE．
又∵∠BEC=∠A+∠ACE，∠BCE=∠BCD+∠DCE，
∴∠BEC=∠BCE，
∴BC=BE．
故选C．
点睛：本题考查了直角三角形的性质、三角形外角的性质、余角、角平分线的定义以及等腰三角形的判定，通过角的计算找出∠BEC=∠BCE是解题的关键．
4．D
【解析】
【分析】
根据直角三角形两锐角互余求出∠CBD，再根据角平分线的定义求解即可得答案.
【详解】
∵CD⊥BD，∠C=55°，
∴∠CBD=90°-55°=35°，
∵BD平分∠ABC，
∴∠ABC=2∠CBD=2×35°=70°，
故选D．
【点睛】
本题考查了直角三角形两锐角互余的性质，角平分线的定义，熟记性质是解题的关键．
5．A
【解析】【分析】先依据平行线的性质可求得∠ABC的度数，然后在直角三角形CBD中可求得∠BCD的度数．
【详解】∵l1∥l2，
∴∠ABC=∠1=50°，
∵CD⊥AB于点D，
∴∠CDB=90°，
∴∠BCD+∠DBC=90°，即∠BCD+50°=90°，
∴∠BCD=40°，
故选A．
【点睛】本题主要考查的是平行线的性质、垂线的定义、直角三角形两锐角互余的性质，掌握相关知识是解题的关键．
6．A
【解析】∵AB=AC，BD=CD，∠BAD=20°，∴∠CAD=∠BAD=20°，AD⊥BC，∴∠ADC=90°，∵DE⊥AC，∴∠ADE=90°﹣∠CAD=70°，∴∠EDC=∠ADC﹣∠ADE=90°﹣70°=20°，故选A．
7．B
【解析】
【分析】
连结AF．由AB=AD，F是BD的中点，根据等腰三角形三线合一的性质得出AF⊥BD．再根据直角三角形斜边上的中线等于斜边的一半求得AC=2EF=4.
【详解】
解：如图，连结AF．
∵AB=AD，F是BD的中点，
∴AF⊥BD．
∵在Rt△ACF中，∠AFC=90°，E是AC的中点，EF=2，
∴AC=2EF=4．
故选：B.
【点睛】
本题考查了直角三角形斜边上的中线的性质：在直角三角形中，斜边上的中线等于斜边的一半．利用等腰三角形三线合一的性质得出AF⊥BD是解题的关键.
8．D
【解析】∵，
∴，
∴，
又∵在中， 是中点，
∴，
∴，
∴，
∴在四边形中， ，
故选．
9．10
【解析】
【分析】
根据直角三角形斜边上的中线是斜边的一半可以解答本题．
【详解】
∵△ABC中，CD⊥AB于D，E是AC的中点，
∴∠CDA=90°，△ADC是直角三角形，
∴AC=2DE，
∵DE=5，
∴AC=10，
故答案为：10．
【点睛】
本题考查直角三角形斜边上的中线，解答本题的关键是明确题意，利用数形结合的思想解答．
10．3
【解析】因为∠A=∠ABC，所以CA=CB，因为BD⊥AC，所以∠BDC=90°.
因为E为CB的中点，所以BC=2DE，所以6=2DE，则DE=3.
故本题应填3.
11．5
【解析】∵∠ACB=90°，CA=CB，∴△ABC是等腰直角三角形，∵AB=10cm，∴斜边上的高CD=AB=5cm．故答案为：5．
12．35°
【解析】
【分析】
根据直角三角形两锐角互余可得，然后解方程组即可．
【详解】
解：，
，
比大，
，
得，，
．
故答案为：．
【点睛】
本题考查了三角形的内角和，直角三角形两锐角互余的性质，熟记性质并列出关于、的两个方程是解题的关键．
13．68
【解析】∵∠B=∠C，
∴∠BDE=∠CFD=180°﹣158°=22°，
∵FD⊥BC于D，DE⊥AB于E，
∴∠EDF=∠C=90°﹣22°=68°，
故答案为：68．
14．8
【解析】∵AB=AC， AF⊥BC，∴∠AFB=90°，BF=CF，又∵BE⊥AC，∴∠BEC=∠BEA=90°，∴EF= BC=3，又∵D为AB中点，∴DE=DF= AB，∵DE+DF+EF=11，∴DE+DF=8，∴AB=8.
15．70°．
【解析】【分析】在直角△EBD中，利用直角三角形两锐角互余求得∠B的度数，根据直角三角形斜边中线等于斜边的一半，可得AD=BD，从而得∠BAD=∠B=55°，再根据三角形内角和定理即可求得.
【详解】∵ED⊥BC，∴∠BDE=90°，
又∵∠E=35°，
∴∠B=90°-∠E=55°，
∵在Rt△ABC中，∠BAC=90°，AD是BC边上的中线，
∴AD=BD，
∴∠BAD=∠B=55°，
∴∠BDA=180°-∠B-∠BAD=70°．
【点睛】本题考查了直角三角形的性质，三角形内角和定理等，熟练掌握直角三角形斜边中线等于斜边一半是解题的关键.
16．见解析
【解析】
【分析】
根据直角三角形斜边上的中线等于斜边的一半可得BE=AC，DE=AC，从而得到BE=DE，再根据等腰三角形三线合一的性质证明．
【详解】
证明：∵∠ABC＝∠ADC＝90°，
∴△ABC和△ADC都是直角三角形．
又∵E是AC的中点，
∴BE＝DE＝AC.
又∵EF平分∠BED，
∴EF⊥BD.
【点睛】
本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，熟记性质是解题的关键．
17．详见解析.
【解析】
【分析】
根据角平分线的定义可得，再根据等角的余角相等求出，然后根据对顶角相等可得，等量代换即可得解．
【详解】
证明：平分，
，
，，
，
，
对顶角相等，
.
【点睛】
本题考查了直角三角形的性质，等角的余角相等的性质，熟记各性质并准确识图是解题的关键．
18．（1）详见解析；（2）
【解析】
【分析】
Ⅰ以C为圆心CA为半径画弧交CB于D，作即可；
Ⅱ先由等腰三角形的性质求出，再在在中根据直角三角形两锐角互余计算即可；
【详解】
解：Ⅰ如图，点D就是所求作的点，线段AD，DE就是所要作的线段．
Ⅱ，
，
在中，
．
【点睛】
本题考查作图复杂作图，等腰三角形的性质，直角三角形两锐角互余，解题的关键是熟练掌握基本知识，属于中考常考题型
19．（1）15°（2）证明见解析
【解析】
【分析】
（1）由图示知∠DCE=∠DCB-∠ECB，由∠B=30°，CD⊥AB于D，利用内角和定理，求出∠DCB的度数，又由角平分线定义得∠ECB=∠ACB，则∠DCE的度数可求；（2）根据∠CEF+∠ECB=180°，由同旁内角互补，两直线平行可以证明EF∥BC．
【详解】
（1）∵∠B=30°，CD⊥AB于D，
∴∠DCB=90°-∠B=60°，
∵CE平分∠ACB，∠ACB=90°，
∴∠ECB=∠ACB=45°，
∴∠DCE=∠DCB-∠ECB=60°-45°=15°；
（2）∵∠CEF=135°，∠ECB=∠ACB=45°，
∴∠CEF+∠ECB=180°，
∴EF∥BC．
【点睛】
本题考查了直角三角形的性质、角的和差、平行线的判定等，熟练掌握相关的性质与定理是解题的关键.
20．(1)见解析；(2)△ABC是等腰直角三角形．理由见解析；(3)AM＝BC.理由见解析.
【解析】分析：（1）AC=AB，可通过证明△ADC≌△AEB得到；?
（2）△ABC是等腰直角三角形，由（1）可知△ABC是等腰三角形，再证明∠CAB=90°即可；?
（3）?AM＝BC，根据等腰三角形的性质：三线合一证明即可．
详解：(1)在△ACD和△BAE中，
∵CD＝AE，∠CDA＝∠AEB＝90°，AD＝BE，
∴△ACD≌△BAE(SAS)．∴AC＝BA.
(2)△ABC是等腰直角三角形．理由如下：
由(1)知△ACD≌△BAE，
∴AC＝BA，∠CAD＝∠ABE，
∴∠BAC＝180°－∠CAD－∠BAE＝180°－∠ABE－∠BAE＝180°－90°＝90°.
∴△ABC为等腰直角三角形．
(3)AM＝BC.理由如下：
∵△ABC为等腰直角三角形，且AM⊥BC，
∴BM＝CM，∴AM＝BC.
点睛：本题考查了全等三角形的判定和性质、等腰三角形的判定和性质,直角三角形斜边中线的性质，证明△ACD≌△BAE是解答本题的关键.
21．(1)∠EFD＝∠C－∠B.（2）成立，理由见解析.
【分析】先根据AE平分∠BAC推出∠BAE=∠BAC=[180°-（∠B+∠C）]，再根据外角的定义求出∠FED=∠B+∠BAE，然后利用直角三角形的性质求出∠EFD=90°-∠FED．
【详解】
解：(1)∠EFD＝∠C－∠B.
理由如下：由AE是∠BAC的平分线知∠BAE＝∠BAC.
由三角形外角的性质知∠FED＝∠B＋∠BAC，
故∠B＋∠BAC＋∠EFD＝90°①.
在△ABC中，由三角形内角和定理得
∠B＋∠BAC＋∠C＝180°，
即∠C＋∠B＋∠BAC＝90°②.
②－①，得∠EFD＝∠C－∠B.
(2)成立．
理由如下：由对顶角相等和三角形的外角性质知：∠FED＝∠AEC＝∠B＋∠BAC，
故∠B＋∠BAC＋∠EFD＝90°①.
在△ABC中，由三角形内角和定理得：
∠B＋∠BAC＋∠C＝180°，即∠B＋∠BAC＋∠C＝90°②.②－①，得∠EFD＝∠C－∠B.
【点睛】
此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质，命题时经常将多个知识点联系在一起进行考查，这样更能训练学生的解题能力．