2.7 探索勾股定理(2)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 2.7 探索勾股定理(2)(知识清单+经典例题+夯实基础+提优训练+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 343.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-14 19:52:32 | ||
图片预览


文档简介
浙江版八年级数学上册第2章特殊三角形2.7探索勾股定理
第1课时 探索勾股定理(1)2
【知识清单】
1、运用拼图的方法验证勾股定理,关键是利用不同的方法表示 .
2、勾股定理是 三角形特有的性质,其余三角形不具有此性质.
【经典例题】
例题1,如图,在△ABC中,∠C=90°,∠BAC=3∠B, BC=1m,则AC的长为________m.
【分析】本题考查的是直角三角形的性质、三角形内角与外角的关系,根据知识点作出解答.
【解答】如图,作∠BAD=∠B,AD交BC于D,
∴BD=AD,
∵∠BAC=3∠B,∠BAC+∠B=90°,
∴3∠B+∠B=90°,
∴∠B=22.5°.
∴∠B=∠BAD=22.5°.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=22.5°+22.5°=45°.
∵∠C=90°,
∴∠DAC=90°-∠ADC=90°-45°=45°.
∴DC=AC.
设DC=x,则BD=,
在Rt△ADC中,,
∴.
∵BD=AD,
∴.
解得,.
∴.
【点评】本题是一道综合性的题目,需要同学们把直角三角形的性质和三角形内角与外角的关系结合起来解答.
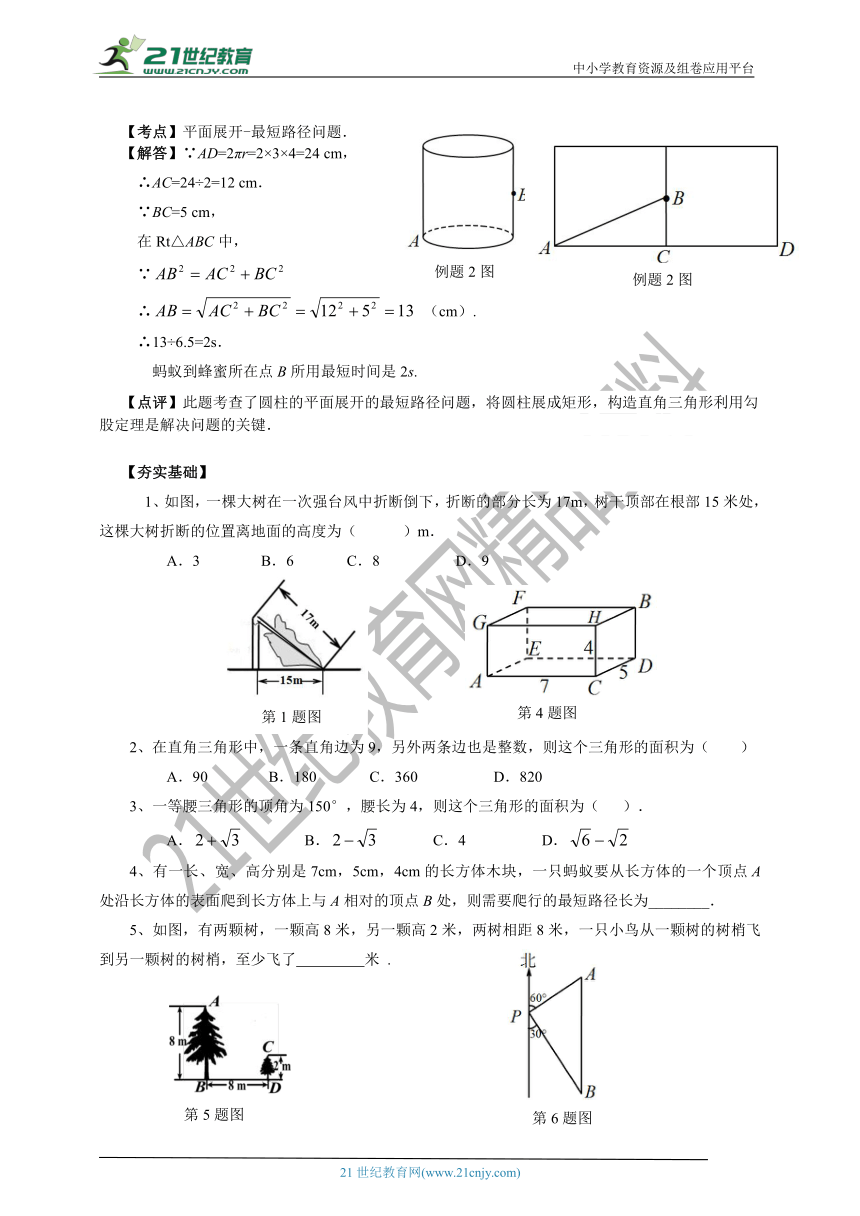
例题1,如图,圆柱的高为10cm,底面半径为4cm,点B离地面5cm,点B处有一滴蜂蜜,一只蚂蚁以6.5cm/s的速度从底面上的点A处绕曲面到达点B吃蜂蜜,蚂蚁到蜂蜜所在点B所用最短时间是多少?(π取3)如图,AB就是蚂蚁爬的最短路径.
【分析】先将图形展开,根据两点之间,线段最短,利用根据勾股定理即可得出结论.
【考点】平面展开-最短路径问题.
【解答】∵AD=2πr=2×3×4=24 cm,
∴AC=24÷2=12 cm.
∵BC=5 cm,
在Rt△ABC中,
∵
∴ (cm).
∴13÷6.5=2s.
蚂蚁到蜂蜜所在点B所用最短时间是2s.
【点评】此题考查了圆柱的平面展开的最短路径问题,将圆柱展成矩形,构造直角三角形利用勾股定理是解决问题的关键.
【夯实基础】
1、如图,一棵大树在一次强台风中折断倒下,折断的部分长为17m,树干顶部在根部15米处,这棵大树折断的位置离地面的高度为( )m.
A.3 B.6 C.8 D.9
2、在直角三角形中,一条直角边为9,另外两条边也是整数,则这个三角形的面积为( )
A.90 B.180 C.360 D.820
3、一等腰三角形的顶角为150°,腰长为4,则这个三角形的面积为( ).
A. B. C.4 D.
4、有一长、宽、高分别是7cm,5cm,4cm的长方体木块,一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上与A相对的顶点B处,则需要爬行的最短路径长为________.
5、如图,有两颗树,一颗高8米,另一颗高2米,两树相距8米,一只小鸟从一颗树的树梢飞到另一颗树的树梢,至少飞了 米 .
6、一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为40海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处.求此时轮船所在的B处与灯塔P的距离 海里(结果保留根号).
7、若直角三角形的两条边长为3cm、4cm,则斜边的中线长为________.
8、如图,将长方形(四个角都是直角,对边相等)ABCD沿AF折叠,使点B落在DC边的点E处,已知AB=15cm,BC=12cm,求FC的长.
【提优特训】
9、在边长为4的等边ΔABC中,BD是AC边的高,
E、F分别为BD和AB上的动点(点F不与点A、
B重合,点E不与点B、D重合),则EF+EA的
最小值为( )
A.4 B.3 C. D.2
10、在ΔABC中,∠A︰∠B︰∠C=3︰2︰1,a、b、c分别为∠A,∠B,∠C的对边,
则a︰b︰c等于( )
A.︰︰ B.︰︰ C.︰︰ D.︰︰
11、如图是飞机的悬梯侧面视图如图所示,其中AB=20米,BC=12米,∠C=90°,悬梯的宽度为4米,因重要的外事活动要求铺设红色地毯,则在AB段楼梯所铺地毯的面积应为( )米2.
A.144 B.128 C.112 D.80
12、如图,已知△ABC是直角三角形,分别以其三边为直径作半圆,则图中阴影部分的面积与△ABC的面积关系为 (填“>”“=”“<”).
13、如图,如果以第一个正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的边长为,按上述方法所作的正方形的边长依次为a2,a3,…,an(n为正整数),那么第n个正方形的边长an等于 .
14、如图①是直角边分别为a、b,斜边为c的直角三角形,用四个图①的三角形拼成图②的正方形,请你根据图②的图形验证勾股定理.
15、如图,在Rt△ABC中,∠ACB=90°,AC=8,
BC=6,将△ABC扩充为等腰三角形ABD,且扩充
部分是以4为直角边的直角三角形,求CD的长.
16、如图,在四边形ABDC中,AB=AC=15cm,∠A=60°,
∠ACD=150°,已知四边形ABDC的周长为75cm,
求四边形ABCD的面积.
17、如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?
【中考链接】
18、2018陕西6、如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为
A. B. C. D.
19、2018?泸州8.(3分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
20、2018青岛6.(3分)如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕现交于点F.已知EF=,则BC的长是( )
A. B. C.3 D.
参考答案
知识清单1、相同面积 2、直角三角形5、
1、C 2、B 3、C 4、 5、10 6、 7、2.5或2 9、C 10、D 11、C
12、= 13、 18、C 19、D 20、B
8、解:在 Rt△ADE中,∠D=90°,AD=BC=12 cm,AE=AB=15,
∴,
∴ (cm).
∴EC=DC-DE=15-9=6(cm).?
设:FC=xcm,则FB=(12-x)cm、EF=(12-x)cm?,
在 Rt△EFC中,EF2=EC2+FC2?,
∴(12-x)2=62+x2?,
解得,x=4.5.
∴FC的长为4.5cm.
14、解答: 根据图形②可知:4个直角三角形面积的和
+正方形EFGH的面积=正方形ABCD的面积,
即.
所以.
15、解:分三种情况:
(1)当AD=AB时,
如图①所示:
则CD=BC=6;
(2)当AD=BD时,
如图②所示:
设CD=x,则AD=x+6,
在Rt△ADC中,由勾股定理得:
,即,
解得:,
;
(3)当BD=AB时,
如图③所示:
在Rt△ABC中,,
∴BD=AB=10,
∴CD=10-6=4;
综上所述:CD的长为6或或4.
16、解答:连接BC,
∵AB=AD=15cm,∠A=60°,
∴△ABD是等边三角形.
∴AB=BC=AC=15 cm,
∵∠ACD=150°
∴∠BCD=150°-60°=90°,
∴△BCD是直角三角形,
又∵四边形ABDC的周长为75cm,
∴BD+DC=75-AC-AB=75-15-15=45cm,
设CD=x,则BD=45-x,
根据勾股定理得到
即
解得: cm
∴,.
四边形ABCD的面积.
17、解答:设BD高为x,则从B点爬到D点再沿直线DA到A点,走的总路程为x+AD,其中.
而从B点到A点经过路程(20+10)m=30m,
根据路程相同列出方程,
,
两边平方得:,
整理得:80x=400,
解得:x=5,
所以这棵树的高度为10+5=15m.
故答案为:15m.
第1课时 探索勾股定理(1)2
【知识清单】
1、运用拼图的方法验证勾股定理,关键是利用不同的方法表示 .
2、勾股定理是 三角形特有的性质,其余三角形不具有此性质.
【经典例题】
例题1,如图,在△ABC中,∠C=90°,∠BAC=3∠B, BC=1m,则AC的长为________m.
【分析】本题考查的是直角三角形的性质、三角形内角与外角的关系,根据知识点作出解答.
【解答】如图,作∠BAD=∠B,AD交BC于D,
∴BD=AD,
∵∠BAC=3∠B,∠BAC+∠B=90°,
∴3∠B+∠B=90°,
∴∠B=22.5°.
∴∠B=∠BAD=22.5°.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=22.5°+22.5°=45°.
∵∠C=90°,
∴∠DAC=90°-∠ADC=90°-45°=45°.
∴DC=AC.
设DC=x,则BD=,
在Rt△ADC中,,
∴.
∵BD=AD,
∴.
解得,.
∴.
【点评】本题是一道综合性的题目,需要同学们把直角三角形的性质和三角形内角与外角的关系结合起来解答.
例题1,如图,圆柱的高为10cm,底面半径为4cm,点B离地面5cm,点B处有一滴蜂蜜,一只蚂蚁以6.5cm/s的速度从底面上的点A处绕曲面到达点B吃蜂蜜,蚂蚁到蜂蜜所在点B所用最短时间是多少?(π取3)如图,AB就是蚂蚁爬的最短路径.
【分析】先将图形展开,根据两点之间,线段最短,利用根据勾股定理即可得出结论.
【考点】平面展开-最短路径问题.
【解答】∵AD=2πr=2×3×4=24 cm,
∴AC=24÷2=12 cm.
∵BC=5 cm,
在Rt△ABC中,
∵
∴ (cm).
∴13÷6.5=2s.
蚂蚁到蜂蜜所在点B所用最短时间是2s.
【点评】此题考查了圆柱的平面展开的最短路径问题,将圆柱展成矩形,构造直角三角形利用勾股定理是解决问题的关键.
【夯实基础】
1、如图,一棵大树在一次强台风中折断倒下,折断的部分长为17m,树干顶部在根部15米处,这棵大树折断的位置离地面的高度为( )m.
A.3 B.6 C.8 D.9
2、在直角三角形中,一条直角边为9,另外两条边也是整数,则这个三角形的面积为( )
A.90 B.180 C.360 D.820
3、一等腰三角形的顶角为150°,腰长为4,则这个三角形的面积为( ).
A. B. C.4 D.
4、有一长、宽、高分别是7cm,5cm,4cm的长方体木块,一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上与A相对的顶点B处,则需要爬行的最短路径长为________.
5、如图,有两颗树,一颗高8米,另一颗高2米,两树相距8米,一只小鸟从一颗树的树梢飞到另一颗树的树梢,至少飞了 米 .
6、一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为40海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处.求此时轮船所在的B处与灯塔P的距离 海里(结果保留根号).
7、若直角三角形的两条边长为3cm、4cm,则斜边的中线长为________.
8、如图,将长方形(四个角都是直角,对边相等)ABCD沿AF折叠,使点B落在DC边的点E处,已知AB=15cm,BC=12cm,求FC的长.
【提优特训】
9、在边长为4的等边ΔABC中,BD是AC边的高,
E、F分别为BD和AB上的动点(点F不与点A、
B重合,点E不与点B、D重合),则EF+EA的
最小值为( )
A.4 B.3 C. D.2
10、在ΔABC中,∠A︰∠B︰∠C=3︰2︰1,a、b、c分别为∠A,∠B,∠C的对边,
则a︰b︰c等于( )
A.︰︰ B.︰︰ C.︰︰ D.︰︰
11、如图是飞机的悬梯侧面视图如图所示,其中AB=20米,BC=12米,∠C=90°,悬梯的宽度为4米,因重要的外事活动要求铺设红色地毯,则在AB段楼梯所铺地毯的面积应为( )米2.
A.144 B.128 C.112 D.80
12、如图,已知△ABC是直角三角形,分别以其三边为直径作半圆,则图中阴影部分的面积与△ABC的面积关系为 (填“>”“=”“<”).
13、如图,如果以第一个正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的边长为,按上述方法所作的正方形的边长依次为a2,a3,…,an(n为正整数),那么第n个正方形的边长an等于 .
14、如图①是直角边分别为a、b,斜边为c的直角三角形,用四个图①的三角形拼成图②的正方形,请你根据图②的图形验证勾股定理.
15、如图,在Rt△ABC中,∠ACB=90°,AC=8,
BC=6,将△ABC扩充为等腰三角形ABD,且扩充
部分是以4为直角边的直角三角形,求CD的长.
16、如图,在四边形ABDC中,AB=AC=15cm,∠A=60°,
∠ACD=150°,已知四边形ABDC的周长为75cm,
求四边形ABCD的面积.
17、如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?
【中考链接】
18、2018陕西6、如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为
A. B. C. D.
19、2018?泸州8.(3分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
20、2018青岛6.(3分)如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕现交于点F.已知EF=,则BC的长是( )
A. B. C.3 D.
参考答案
知识清单1、相同面积 2、直角三角形5、
1、C 2、B 3、C 4、 5、10 6、 7、2.5或2 9、C 10、D 11、C
12、= 13、 18、C 19、D 20、B
8、解:在 Rt△ADE中,∠D=90°,AD=BC=12 cm,AE=AB=15,
∴,
∴ (cm).
∴EC=DC-DE=15-9=6(cm).?
设:FC=xcm,则FB=(12-x)cm、EF=(12-x)cm?,
在 Rt△EFC中,EF2=EC2+FC2?,
∴(12-x)2=62+x2?,
解得,x=4.5.
∴FC的长为4.5cm.
14、解答: 根据图形②可知:4个直角三角形面积的和
+正方形EFGH的面积=正方形ABCD的面积,
即.
所以.
15、解:分三种情况:
(1)当AD=AB时,
如图①所示:
则CD=BC=6;
(2)当AD=BD时,
如图②所示:
设CD=x,则AD=x+6,
在Rt△ADC中,由勾股定理得:
,即,
解得:,
;
(3)当BD=AB时,
如图③所示:
在Rt△ABC中,,
∴BD=AB=10,
∴CD=10-6=4;
综上所述:CD的长为6或或4.
16、解答:连接BC,
∵AB=AD=15cm,∠A=60°,
∴△ABD是等边三角形.
∴AB=BC=AC=15 cm,
∵∠ACD=150°
∴∠BCD=150°-60°=90°,
∴△BCD是直角三角形,
又∵四边形ABDC的周长为75cm,
∴BD+DC=75-AC-AB=75-15-15=45cm,
设CD=x,则BD=45-x,
根据勾股定理得到
即
解得: cm
∴,.
四边形ABCD的面积.
17、解答:设BD高为x,则从B点爬到D点再沿直线DA到A点,走的总路程为x+AD,其中.
而从B点到A点经过路程(20+10)m=30m,
根据路程相同列出方程,
,
两边平方得:,
整理得:80x=400,
解得:x=5,
所以这棵树的高度为10+5=15m.
故答案为:15m.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
