第2章 有理数的运算单元测试卷B(含解析)
文档属性
| 名称 | 第2章 有理数的运算单元测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-15 07:49:39 | ||
图片预览




文档简介
第二章有理数的运算单元测试卷B
一.选择题(共10小题,3*10=30)
1.如图,在一个由6个圆圈组成的三角形里,把1到6这6个数分别填入图的圆圈中,要求三角形的每条边上的三个数的和S都相等,那么S的最大值是( )
?
A.9 B.10 C.12 D.13
2.m是有理数,则m+|m|( )
A.可以是负数 B.不可能是负数
C.一定是正数 D.可是正数也可是负数
3.下列说法正确的有( )①所有的有理数都能用数轴上的点表示;②符号不同的两个数互为相反数;③有理数分为正数和负数;④两数相减,差一定小于被减数;⑤两数相加,和一定大于任何一个加数.
A.4个 B.2个 C.1个 D.3个
4.99,这个运算应用了( )
A.加法交换律 B.乘法结合律
C.乘法交换律、乘法结合律 D.乘法分配律
5.下列算式中,与相等的是( )
A. B.5 C.5 D.5
6.若(x﹣2)2与|5+y|互为相反数,则yx的值( )
A.2 B.﹣10 C.10 D.25
7.一台机器有大、小齿轮用同一转送带连接,若大小齿轮的齿数分别为12和36个,大齿轮每分钟2.5×103转,则小齿轮10小时转( )
A.1.5×106转 B.5×105转 C.4.5×106转 D.15×106转
8.近似数35.04万精确到( )
A.百位 B.百分位 C.万位 D.个位
9.若S=15+195+1995+19995+….+,则S的末四位数字的和为( )
A.10 B.14 C.18 D.20
10.梵帝冈是世界上最小的国家,它的面积仅有0.44千米2,相当于天安门广场的面积.请你估计一下,梵帝冈的百万分之一大约相当于( )
A.一间教室地面的面积 B.一个操场的面积
C.一只铅笔盒盒面的面积 D.一张课桌面的面积
二.填空题(共8小题,3*8=24)
11.某冬天中午的温度是5℃,下午上升到7℃,由于冷空气南下,到夜间又下降了9℃,则这天夜间的温度是 ℃.
12.已知|x|=3,|y|=8,且xy<0,则x+y的值等于 .
13.把40,44,45,63,65,78,99,105平均分成两组,并且使这两组数的乘积相等,直接写出分组情况: .
14.计算:+++…+= .
15.定义一种新运算:1!=1,2!=1×2,3!=1×2×3,4!=1×2×3×4,……计算:= .
16.有一个运算程序,可以使:a⊕b=n(n为常数)时,得(a+1)⊕b=n+1,a⊕(b+1)=n﹣2,现在已知1⊕1=2,那么3⊕3= .
17.若定义一种新的运算“△”,规定有理数a△b=a﹣b,如2△3=2﹣3=1,则(﹣2)△(﹣3)= .
18.所有分母不超过2003的正的真分数的和等于 .
三.解答题(共8小题,66分)
19.(8分)阅读下列内容,并完成相关问题:
小明说:“我定义了一种新的运算,叫?(加乘)运算.”然后他写出了一些按照?(加乘)运算的运算法则进行运算的算式:
(+4)?(+2)=+6;(﹣4)?(﹣3)=+7;
(﹣5)?(+3)=﹣8;(+6)?(﹣7)=﹣13;
(+8)?0=8;0?(﹣9)=9.
小亮看了这些算式后说:“我知道你定义的?(加乘)运算的运算法则了.”
聪明的你也明白了吗?
(1)归纳?(加乘)运算的运算法则:
两数进行?(加乘)运算时, .
特别地,0和任何数进行?(加乘)运算,或任何数和0进行?(加乘)运算, .
(2)计算:[(﹣2)?(+3)]?[(﹣12)?0](括号的作用与它在有理数运算中的作用一致)
(3)我们知道加法有交换律和结合律,这两种运算律在有理数的?(加乘)运算中还适用吗?请你任选一个运算律,判断它在?(加乘)运算中是否适用,并举例验证.(举一个例子即可)”
20.(8分)计算题:
(1)﹣(+3.7)+(+)﹣(﹣1.7)
(2)﹣27÷2×
(3)(﹣+﹣)×(﹣24)
(4)﹣24+|3﹣4|﹣2×(﹣1)2006.
21.(6分)若“*”是一种新的运算符号,并且规定a*b=.例如:3*5=,求[2*(﹣2)]*(﹣3)的值.
22.(10分)观察下列每对数在数轴上的对应点间的距离,并回答下列问题:
4与﹣2,3与5,﹣2与﹣6,﹣4与3
(1)你能发现所得距离与这两个数的差的绝对值有什么关系吗?
(2)若数轴上的点A表示的数为x,点B表示的数为﹣1,则A与B两点间的距离可以表示为什么?
(3)结合数轴求|x﹣2|+|x+3|的最小值,并求出取得最小值时x的取值范围;
(4)求满足|x+1|+|x+4|>3的x的取值范围.
23.(8分)有一些分别标有6,12,18,24,…一这些数的卡片,后一张卡片上的数比前一张卡片上的数大6,小明拿了三张相邻的卡片,且这三张卡片上的数字之和为342.
(1)小明拿到了哪三张卡片?
(2)你能拿到相邻的三张卡片,使得这三张卡片上的数之和是86吗?请说明理由.
24.(8分)实数a,b,c在数轴上的位置如图所示,化简|c|﹣|a|+|﹣b|+|﹣a|.
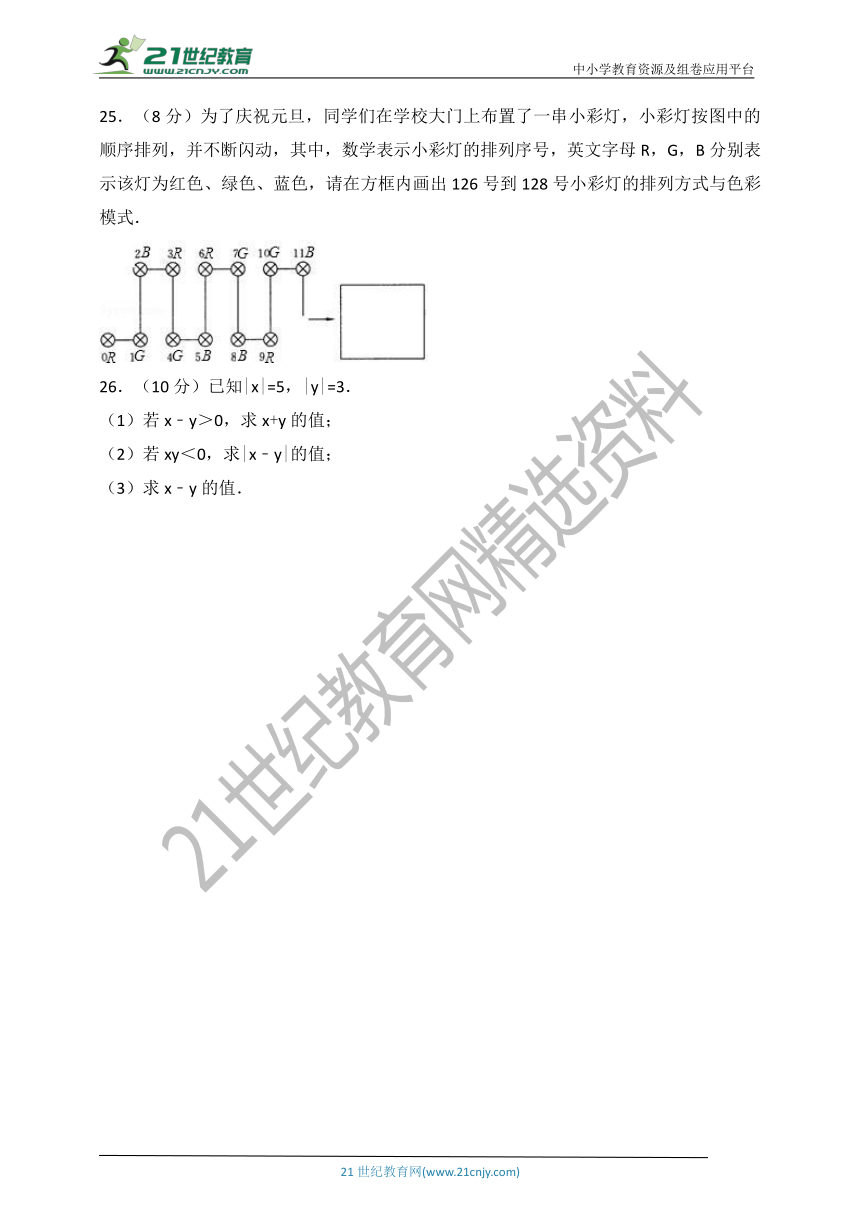
25.(8分)为了庆祝元旦,同学们在学校大门上布置了一串小彩灯,小彩灯按图中的顺序排列,并不断闪动,其中,数学表示小彩灯的排列序号,英文字母R,G,B分别表示该灯为红色、绿色、蓝色,请在方框内画出126号到128号小彩灯的排列方式与色彩模式.
26.(10分)已知|x|=5,|y|=3.
(1)若x﹣y>0,求x+y的值;
(2)若xy<0,求|x﹣y|的值;
(3)求x﹣y的值.
参考答案与试题解析
1.解:由图可知S=3+4+5=12.
故选:C.
2.解:当m>0时,m+|m|>0,
当m=0时,m+|m|=0,
当m<0时,m+|m|=0,
故选:B.
3.解:①所有的有理数都能用数轴上的点表示,说法正确;
②只有符号不同的两个数叫做互为相反数,故此选项错误;
③有理数分为正数和负数、零,故此选项错误;
④两数相减,差一定小于被减数,两负数相减的不同,故此选项错误;
⑤两数相加,和一定大于任何一个加数,异号两数相加,则不同,故此选项错误.
故选:C.
4.解:99,这个运算应用了乘法的分配律,
故选:D.
5.解:A、5×=≠,选项错误;
B、5÷=5×=≠,选项错误;
C、5+=5,选项正确;
D、5﹣=4≠,选项错误.
故选:C.
6.解:∵(x﹣2)2与|5+y|互为相反数,
∴(x﹣2)2+|5+y|=0,
∴x﹣2=0,5+y=0,
解得x=2,y=﹣5,
所以,yx=(﹣5)2=25.
故选:D.
7.解:小齿轮10小时转60×2.5×103×10×(36÷12)=4.5×106转.故选C.
8.解:∵35.04万末尾数字4表示4百,
∴近似数35.04万精确到百位.
故选:A.
9.解:15=20﹣5,195=200﹣5,1995=2000﹣5,…,199…5=2×102011﹣5,
故S=15+195+1995+19995+….+=20+200+2000+…+2×1099﹣2011×5,
22220﹣2011×5=12165,
S的末四位数字为12165,
则S的末四位数字的和为1+2+1+6+5=14.
故选:B.
10.解:∵梵蒂冈的国土面积只有0.44平方千米,
∴它的百万分之一为0.44平方千米×10﹣6=4.4×105平方米×10﹣6=0.44平方米,
所以它的百万分之一大约相当于一张课桌面的面积.
故选:D.
11.解:根据题意得:7﹣9=﹣2(℃).
故答案是:﹣2.
12.解:根据题意得:x=﹣3,y=8,此时x+y=5;x=3,y=﹣8,此时x+y=﹣5,
故答案为:±5
13.解:偶数组:40=2×2×2×5,44=2×2×11,78=2×3×13;
奇数组:45=3×3×5,63=3×3×7,65=5×13,99=3×3×11,105=3×5×7,
(1)先看偶数组,40第一组,44和78第二组(因为40分解出3个2;44有2个2,78有1个2);
(2)44中含有11,则99为第一组;78中含有13,则65为第一组;另外两个分解出含有5的数是45,105,其中105为第二组,
答:第一组有40,99,65,63;第二组为44,78,45,105.
故答案为:40,99,65,63;44,78,45,105.
14.解:原式=(1﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣+﹣)
=(﹣﹣)=,
故答案为:
15.解:根据题意知==99×100=9900,
故答案为:9900.
16.解:现在已知1⊕1=2,求3⊕3,
相当于a增加2,b增加2,结果就是在2的基础上增加2,减少4,即2+2﹣4=0.
17.解:(﹣2)△(﹣3),
=(﹣2)﹣(﹣3),
=﹣2+3,
=1.
故答案为:1.
18.解:依题意有+++…+++…+,
=+1++2+…+1001,
=(+1001)×2002÷2,
=1002501.5.
故答案为:1002501.5.
19.解:(1)归纳?(加乘)运算的运算法则:
两数进行?(加乘)运算时,同号得正、异号得负,并把绝对值相加.
特别地,0和任何数进行?(加乘)运算,或任何数和0进行?(加乘)运算,都得这个数的绝对值,
故答案为:同号得正、异号得负,并把绝对值相加;都得这个数的绝对值.
(2)原式=(﹣5)?12=﹣17;
(3)加法的交换律仍然适用,
例如:(﹣3)?(﹣5)=8,(﹣5)?(﹣3)=8,
所以(﹣3)?(﹣5)=(﹣5)?(﹣3),
故加法的交换律仍然适用.
20.解:(1)原式=+﹣3.7+1.7=1﹣2=﹣1;
(2)原式=﹣27××=﹣;
(3)原式=﹣2+20﹣12+9=24;
(4)原式=﹣16+1﹣2=﹣17.
21.解:原式=*(﹣3)
=0*(﹣3)
=
=﹣.
22.解:(1)所得距离与这两个数的差的绝对值相等;
(2)数轴上的点A表示的数为x,点B表示的数为﹣1,则A与B两点间的距离可以表示为|x+1|;
(3)结合数轴可得|x﹣2|+|x+3|的最小值为5(﹣3≤x≤2);
(4)利用数轴可知|x+1|+|x+4|>3的x的取值范围x<﹣1或x>﹣4;
23.解:(1)设小明拿到的三张相邻的卡片,中间的那张对应的数字为x,
(x﹣6)+x+(x+6)=342,
解得,x=114
∴x﹣6=114﹣6=108,x+6=114+6=120,
即小明拿到的三张相邻的卡片对应的数字是108,114,120;
(2)不能拿到相邻的三张卡片,使得这三张卡片上的数之和是86,
理由:三张相邻的卡片,中间的那张对应的数字为x,
(x﹣6)+x+(x+6)=86,
解得,x=,
由题意可知,卡片上的数字都是整数,故不能拿到相邻的三张卡片,使得这三张卡片上的数之和是86.
24.解:由题意得:b<c<﹣1<0<1<a,
∴原式=﹣c﹣a﹣b+a
=﹣c﹣b.
25.解:小彩灯的排列方式是3个一循环,126÷4的余数是2,
所以126号的位置与2号的位置一样;
色彩模式是3个﹣循环,126÷3=42,能整除,
所以126号的色彩与0号的色彩一样.
如图所示.
26.解:∵|x|=5,
∴x=5或﹣5,
∵|y|=3,
∴y=3或﹣3,
(1)当x﹣y>0时,x=5,y=3或x=5,y=﹣3,
此时x+y=5+3=8或x+y=5+(﹣3)=2,
即x+y的值为:8或2;
(2)当xy<0,
x=5,y=﹣3或x=﹣5,y=3,
此时|x﹣y|=8或|x﹣y|=8,
即|x﹣y|的值为:8;
(3)①x=5时,y=3时,x﹣y=5﹣3=2;
②x=5时,y=﹣3时,x﹣y=5+3=8;
③x=﹣5时,y=3时,x﹣y=﹣5﹣3=﹣8;
④x=﹣5时,y=﹣3时,x﹣y=﹣5+3=﹣2,
综上:x﹣y=±2或±
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
