2.7 探索勾股定理(4)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 2.7 探索勾股定理(4)(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 274.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-21 00:00:00 | ||
图片预览



文档简介
浙江版八年级数学上册第2章特殊三角形2.7探索勾股定理
第2课时 探索勾股定理(2)
【知识清单】
1、勾股定理的逆定理:
如果三角形的三边长a,b,c满足 ,那么这个三角形就是直角三角形.
2、勾股定理的应用:
(1)勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两较短的平方和与较长边的平方作比较;若它们相等时,以a,b,c为三边的三角形是直角三角形;若时,以a,b,c为三边的三角形是钝角三角形;若,时,以a,b,c为三边的三角形是锐角三角形.
(2)定理中a,b,c及只是一种表现形式,不可认为是唯一的,如若三角形三边长a,b,c满足,那么以a,b,c为三边的三角形是直角三角形,这时b为斜边.
(3)描述勾股定理的逆定理时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形.
3、勾股数:?
?①能够构成直角三角形的三边长的三个正整数称为勾股数,即中, a,b,c为正整数,则a,b,c为一组勾股数;
②记住常见的勾股数可以提高解题的速度,3、4、5;6、8、10;5、12、13;7、24、25等;
③用含字母的代数式表示几组勾股数:
;(n≥2,n为正整数);
(n为正整数);
(m>n,m、n均为正整数).
例题1,已知ΔABC的三边a,b,c满足以下条件,试判断ΔABC的形状.
(1)a=2 , b=,c= (2)
【分析】已知三条边判断一个三角形是否为直角三角形的一般步骤如下:(1)确定最长的边;(2)分别计算出最长边的平方与另外两边的平方和;(3)相等则是直角三角形,不等则不是直角三角形.
【解答】(1)∵,
∴ΔABC是直角三角形.
(2)∵,
即,
∴
∴ΔABC是直角三角形.
【点评】本题考查直角三角形勾股定理的逆定理;判定三角形的形状除了用角以外,还可以用有三角形的三边平方来判定,关键分清三角形中最长的边.
例题2, 如图,在四边形ABCD中,∠D=90°,AB=24,BC=26,CD=8,AD=6,求阴影部分的面积.
【分析】先连接AC,在△ADC中利用勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ABC是直角三角形,再根据S阴影部分=S△ABC-S△ADC进行解答即可.
【考点】勾股定理的逆定理、勾股定理.
【解答】连接AC.
在△ADC中,
∵∠D=90°,
∴(勾股定理).
由CD=8,AD=6,
得
在△ABC中,
∵AB=24,BC=26,
∴,
∴∠CAB=90°(勾股定理的逆定理).
因此,
【点评】本题考查的是勾股定理及其逆定理和三角形的面积,根据勾股定理的逆定理判断出△ABC是直角三角形是解答此题的关键.
【夯实基础】
1、以下列各组数为边长,能构成直角三角形的是( )
A.2,4,5 B., , C.15,25,20 D.8,9,10
2、将直角三角形各边缩小相同的倍数,得到三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.任意三角形
3、已知,则以a、b、c为三边长的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4、已知ΔABC中,∠A,∠B,∠C所对的边分别是a,b,c,下列条件的三角形不是直角三角形的是( )
A.a=3b,c=2b B.a︰b︰c=11︰60︰61 C.∠C-∠A=∠B, D.
5、有四根木棒,长度分别为6,8,15,17,若取其中三根木棒组成三角形,有 种取法,其中,能构成直角三角形的是 .
6、三边长为a,b,c满足a+b=15, ab=14.5, c=14,那么此三角形的形状为______.
7、已知△ABC的三边分别为k2-1,2k,k2+1(k>1),则△ABC是 .
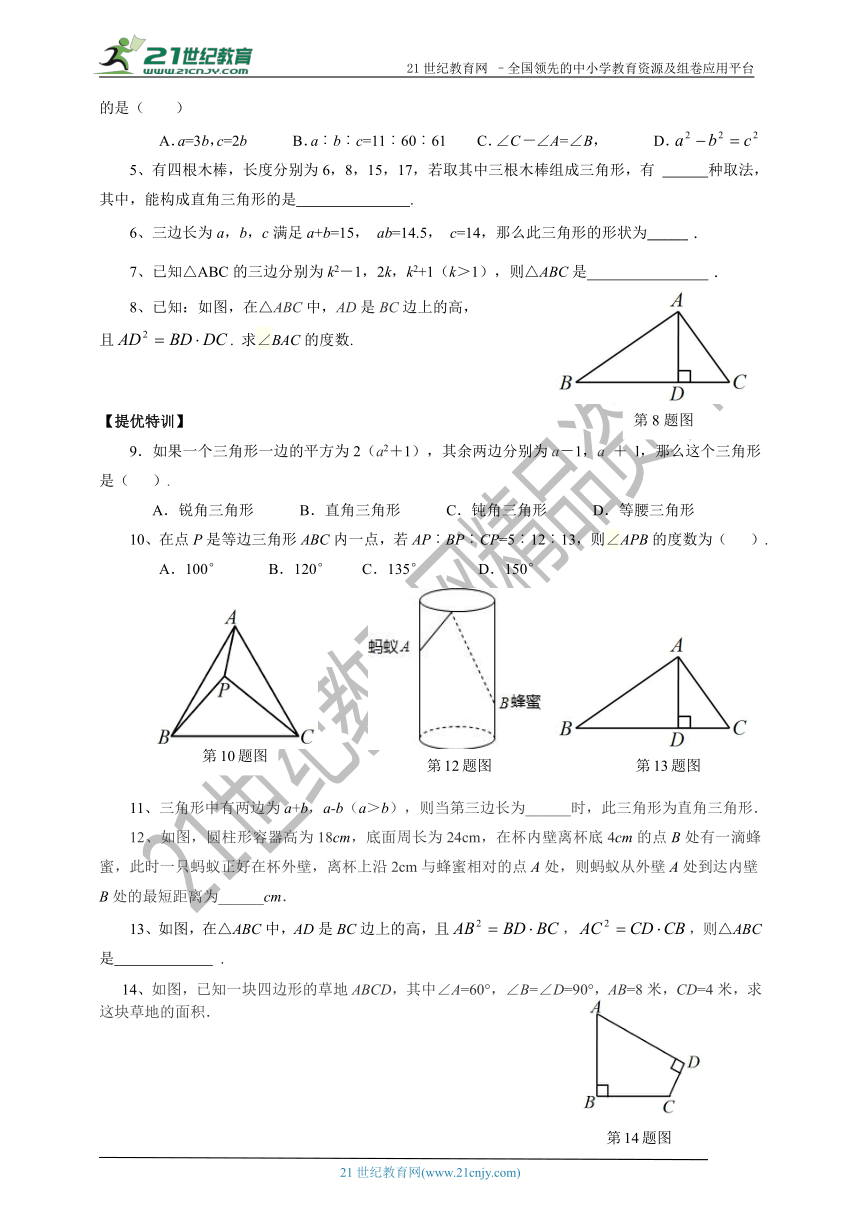
8、已知:如图,在△ABC中,AD是BC边上的高,
且.?求∠BAC的度数.
【提优特训】
9.如果一个三角形一边的平方为2(a2+1),其余两边分别为a-1,a + l,那么这个三角形是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10、在点P是等边三角形ABC内一点,若AP︰BP︰CP=5︰12︰13,则∠APB的度数为( ).
A.100° B.120° C.135° D.150°
11、三角形中有两边为a+b,a-b(a>b),则当第三边长为______时,此三角形为直角三角形.
12、如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为______cm.
13、如图,在△ABC中,AD是BC边上的高,且,,则△ABC是 .
14、如图,已知一块四边形的草地ABCD,其中∠A=60°,∠B=∠D=90°,AB=8米,CD=4米,求这块草地的面积.
15、如图,已知正方形ABCD的边长为8,E为AB中点,F为AD上的一点,且,试判断△EFC的形状.
16、给出一组式子:
①32+42=52,
②52+122=132,
③72+242=252,
④92+402=412,
…
(1)你能发现关于上述式子的一些规律吗?
(2)请你运用规律,或者通过试验的方法,给出第五个式子.
(3)请你根据以上的探究的规律,写出第n个等式,并证明它的正确性.
17、已知a、b、c,是ΔABC的三边,且满足,试判定ΔABC的形状.
【中考链接】
18、2018天津18. 如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上.(1)∠ACB的大小为__________(度);
(2)在如图所示的网格中,P是BC边上任意一点.A为中心,取旋转角等于∠ACB,把点P逆时针旋转,点P的对应点为.当最短时,请用无刻度的直尺,画出点,并简要说明
点的位置是如何找到的(不要求证明)__________.
【答案】 (1).90°; (2). 见解析
19、2018杭州临安22.(6分)阅读下列题目的解题过程:
已知a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状.
20、2018南通17.(3分)如图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B'C,则在旋转过程中点A、C′两点间的最大距离是 .
21、2018湖南湘潭15.(3分)《九章算术》是我国古代最重要的数学著作之一,在“匀股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为 .
参考答案
1、C 2、A 3、B 4、A 5、2, 8,15,17 6、直角三角形 7、直角三角形 9、直角三角形 10、D 11、 12、20 13、直角三角形
8、证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴在Rt△ABD中,根据勾股定理,得,
在Rt△ADC中,根据勾股定理,得,
∴
.
∴△ABC是直角三角形.
∴∠BAC=90°是直角三角形.
14、解答:延长AD,BC,交于点E,
在Rt△ABE中,∠A=60°,AB=8,
∴∠E=30°,AE=2AB=16,
∴.
在Rt△DCE中,∠E=30°,CD=4,
∴CE=2CD=8,
∴.
则
15、解答:△EFC为直角三角形.
∵正方形ABCD的边长为8,
∴AE=EB=4,=2,FD=6,DC=BC=8,
在Rt△AEF中,;
在Rt△DFC中,;
在Rt△EBC中,
∴
∴△EFC是直角三角形.
16、解答:(1)①这些式子每个都呈(a、b、c为正整数)的形式,每个等式中的三个底数都正好组成一组勾股数;②每个等式中a是奇数,a的值等于序数的2倍加1,b为偶数,b的值等于(a-1)乘以序数加1,c奇数c=b+1.④各个式子中,a的取值依次为3,5,7,9,11,是连续增大的奇数.
(2)猜想:第5个式子为112+602=612
(3)第一个数为(2n+1),第二个数为(2n+1-1)(n+1)=2n(n+1),第三个数为2n(n+1)+1
其等式为.
证明:
.
17、解:,
∴ .
∴.
∴.
∴a=9,b=12,c=15.
,
∴.
∴三角形ABC是直角三角形.
18、【解析】分析:(1)利用勾股定理即可解决问题;
(2)如图,取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G;取格点F,连接FG交TC延长线于点,则点即为所求.
详解:(1)∵每个小正方形的边长为1,
∴
∵,
∴ .
∴ΔABC是直角三角形,且∠C=90°.
故答案为90;
(2)如图,即为所求.
点睛:本题考查作图-应用与设计、勾股定理等知识,解题的关键是利用数形结合的思想解决问题,学会用转化的思想思考问题.
19、解:∵a2c2﹣b2c2=a4﹣b4 (A)
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2) (B)
∴c2=a2+b2 (C)
∴△ABC是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: C ;
(2)错误的原因为: 没有考虑a=b的情况 ;
(3)本题正确的结论为: △ABC是等腰三角形或直角三角形 .
【分析】(1)根据题目中的书写步骤可以解答本题;
(2)根据题目中B到C可知没有考虑a=b的情况;
(3)根据题意可以写出正确的结论.
【解答】解:(1)由题目中的解答步骤可得,
错误步骤的代号为:C,
故答案为:C;
(2)错误的原因为:没有考虑a=b的情况,
故答案为:没有考虑a=b的情况;
(3)本题正确的结论为:△ABC是等腰三角形或直角三角形,
故答案为:△ABC是等腰三角形或直角三角形.
【点评】本题考查因式分解的应用、勾股定理的逆定理,解答本题的关键是明确题意,写出相应的结论,注意考虑问题要全面.
20、【分析】连接OA,AC′,如图,易得OC=2,
再利用勾股定理计算出OA=,接着利用
旋转的性质得OC′=OC=2,根据三角形三边的
关系得到AC′≤OA+OC′(当且仅当点A、O、C′
共线时,取等号),从而得到AC′的最大值.
【解答】解:连接OA,AC′,如图,
∵点O是BC中点,
∴OC=BC=2,
在Rt△AOC中,OA==,
∵△ABC绕点O旋转得△A′B'C′,
∴OC′=OC=2,
∵AC′≤OA+OC′(当且仅当点A、O、C′共线时,取等号),
∴AC′的最大值为2+,
即在旋转过程中点A、C′两点间的最大距离是2+.
故答案为2+.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
21、【分析】设AC=x,可知AB=10﹣x,再根据勾股定理即可得出结论.
【解答】解:设AC=x,
∵AC+AB=10,
∴AB=10﹣x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10﹣x)2.
故答案为:x2+32=(10﹣x)2.
【点评】本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
第2课时 探索勾股定理(2)
【知识清单】
1、勾股定理的逆定理:
如果三角形的三边长a,b,c满足 ,那么这个三角形就是直角三角形.
2、勾股定理的应用:
(1)勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两较短的平方和与较长边的平方作比较;若它们相等时,以a,b,c为三边的三角形是直角三角形;若时,以a,b,c为三边的三角形是钝角三角形;若,时,以a,b,c为三边的三角形是锐角三角形.
(2)定理中a,b,c及只是一种表现形式,不可认为是唯一的,如若三角形三边长a,b,c满足,那么以a,b,c为三边的三角形是直角三角形,这时b为斜边.
(3)描述勾股定理的逆定理时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形.
3、勾股数:?
?①能够构成直角三角形的三边长的三个正整数称为勾股数,即中, a,b,c为正整数,则a,b,c为一组勾股数;
②记住常见的勾股数可以提高解题的速度,3、4、5;6、8、10;5、12、13;7、24、25等;
③用含字母的代数式表示几组勾股数:
;(n≥2,n为正整数);
(n为正整数);
(m>n,m、n均为正整数).
例题1,已知ΔABC的三边a,b,c满足以下条件,试判断ΔABC的形状.
(1)a=2 , b=,c= (2)
【分析】已知三条边判断一个三角形是否为直角三角形的一般步骤如下:(1)确定最长的边;(2)分别计算出最长边的平方与另外两边的平方和;(3)相等则是直角三角形,不等则不是直角三角形.
【解答】(1)∵,
∴ΔABC是直角三角形.
(2)∵,
即,
∴
∴ΔABC是直角三角形.
【点评】本题考查直角三角形勾股定理的逆定理;判定三角形的形状除了用角以外,还可以用有三角形的三边平方来判定,关键分清三角形中最长的边.
例题2, 如图,在四边形ABCD中,∠D=90°,AB=24,BC=26,CD=8,AD=6,求阴影部分的面积.
【分析】先连接AC,在△ADC中利用勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ABC是直角三角形,再根据S阴影部分=S△ABC-S△ADC进行解答即可.
【考点】勾股定理的逆定理、勾股定理.
【解答】连接AC.
在△ADC中,
∵∠D=90°,
∴(勾股定理).
由CD=8,AD=6,
得
在△ABC中,
∵AB=24,BC=26,
∴,
∴∠CAB=90°(勾股定理的逆定理).
因此,
【点评】本题考查的是勾股定理及其逆定理和三角形的面积,根据勾股定理的逆定理判断出△ABC是直角三角形是解答此题的关键.
【夯实基础】
1、以下列各组数为边长,能构成直角三角形的是( )
A.2,4,5 B., , C.15,25,20 D.8,9,10
2、将直角三角形各边缩小相同的倍数,得到三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.任意三角形
3、已知,则以a、b、c为三边长的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4、已知ΔABC中,∠A,∠B,∠C所对的边分别是a,b,c,下列条件的三角形不是直角三角形的是( )
A.a=3b,c=2b B.a︰b︰c=11︰60︰61 C.∠C-∠A=∠B, D.
5、有四根木棒,长度分别为6,8,15,17,若取其中三根木棒组成三角形,有 种取法,其中,能构成直角三角形的是 .
6、三边长为a,b,c满足a+b=15, ab=14.5, c=14,那么此三角形的形状为______.
7、已知△ABC的三边分别为k2-1,2k,k2+1(k>1),则△ABC是 .
8、已知:如图,在△ABC中,AD是BC边上的高,
且.?求∠BAC的度数.
【提优特训】
9.如果一个三角形一边的平方为2(a2+1),其余两边分别为a-1,a + l,那么这个三角形是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10、在点P是等边三角形ABC内一点,若AP︰BP︰CP=5︰12︰13,则∠APB的度数为( ).
A.100° B.120° C.135° D.150°
11、三角形中有两边为a+b,a-b(a>b),则当第三边长为______时,此三角形为直角三角形.
12、如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为______cm.
13、如图,在△ABC中,AD是BC边上的高,且,,则△ABC是 .
14、如图,已知一块四边形的草地ABCD,其中∠A=60°,∠B=∠D=90°,AB=8米,CD=4米,求这块草地的面积.
15、如图,已知正方形ABCD的边长为8,E为AB中点,F为AD上的一点,且,试判断△EFC的形状.
16、给出一组式子:
①32+42=52,
②52+122=132,
③72+242=252,
④92+402=412,
…
(1)你能发现关于上述式子的一些规律吗?
(2)请你运用规律,或者通过试验的方法,给出第五个式子.
(3)请你根据以上的探究的规律,写出第n个等式,并证明它的正确性.
17、已知a、b、c,是ΔABC的三边,且满足,试判定ΔABC的形状.
【中考链接】
18、2018天津18. 如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上.(1)∠ACB的大小为__________(度);
(2)在如图所示的网格中,P是BC边上任意一点.A为中心,取旋转角等于∠ACB,把点P逆时针旋转,点P的对应点为.当最短时,请用无刻度的直尺,画出点,并简要说明
点的位置是如何找到的(不要求证明)__________.
【答案】 (1).90°; (2). 见解析
19、2018杭州临安22.(6分)阅读下列题目的解题过程:
已知a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状.
20、2018南通17.(3分)如图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B'C,则在旋转过程中点A、C′两点间的最大距离是 .
21、2018湖南湘潭15.(3分)《九章算术》是我国古代最重要的数学著作之一,在“匀股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为 .
参考答案
1、C 2、A 3、B 4、A 5、2, 8,15,17 6、直角三角形 7、直角三角形 9、直角三角形 10、D 11、 12、20 13、直角三角形
8、证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴在Rt△ABD中,根据勾股定理,得,
在Rt△ADC中,根据勾股定理,得,
∴
.
∴△ABC是直角三角形.
∴∠BAC=90°是直角三角形.
14、解答:延长AD,BC,交于点E,
在Rt△ABE中,∠A=60°,AB=8,
∴∠E=30°,AE=2AB=16,
∴.
在Rt△DCE中,∠E=30°,CD=4,
∴CE=2CD=8,
∴.
则
15、解答:△EFC为直角三角形.
∵正方形ABCD的边长为8,
∴AE=EB=4,=2,FD=6,DC=BC=8,
在Rt△AEF中,;
在Rt△DFC中,;
在Rt△EBC中,
∴
∴△EFC是直角三角形.
16、解答:(1)①这些式子每个都呈(a、b、c为正整数)的形式,每个等式中的三个底数都正好组成一组勾股数;②每个等式中a是奇数,a的值等于序数的2倍加1,b为偶数,b的值等于(a-1)乘以序数加1,c奇数c=b+1.④各个式子中,a的取值依次为3,5,7,9,11,是连续增大的奇数.
(2)猜想:第5个式子为112+602=612
(3)第一个数为(2n+1),第二个数为(2n+1-1)(n+1)=2n(n+1),第三个数为2n(n+1)+1
其等式为.
证明:
.
17、解:,
∴ .
∴.
∴.
∴a=9,b=12,c=15.
,
∴.
∴三角形ABC是直角三角形.
18、【解析】分析:(1)利用勾股定理即可解决问题;
(2)如图,取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G;取格点F,连接FG交TC延长线于点,则点即为所求.
详解:(1)∵每个小正方形的边长为1,
∴
∵,
∴ .
∴ΔABC是直角三角形,且∠C=90°.
故答案为90;
(2)如图,即为所求.
点睛:本题考查作图-应用与设计、勾股定理等知识,解题的关键是利用数形结合的思想解决问题,学会用转化的思想思考问题.
19、解:∵a2c2﹣b2c2=a4﹣b4 (A)
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2) (B)
∴c2=a2+b2 (C)
∴△ABC是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: C ;
(2)错误的原因为: 没有考虑a=b的情况 ;
(3)本题正确的结论为: △ABC是等腰三角形或直角三角形 .
【分析】(1)根据题目中的书写步骤可以解答本题;
(2)根据题目中B到C可知没有考虑a=b的情况;
(3)根据题意可以写出正确的结论.
【解答】解:(1)由题目中的解答步骤可得,
错误步骤的代号为:C,
故答案为:C;
(2)错误的原因为:没有考虑a=b的情况,
故答案为:没有考虑a=b的情况;
(3)本题正确的结论为:△ABC是等腰三角形或直角三角形,
故答案为:△ABC是等腰三角形或直角三角形.
【点评】本题考查因式分解的应用、勾股定理的逆定理,解答本题的关键是明确题意,写出相应的结论,注意考虑问题要全面.
20、【分析】连接OA,AC′,如图,易得OC=2,
再利用勾股定理计算出OA=,接着利用
旋转的性质得OC′=OC=2,根据三角形三边的
关系得到AC′≤OA+OC′(当且仅当点A、O、C′
共线时,取等号),从而得到AC′的最大值.
【解答】解:连接OA,AC′,如图,
∵点O是BC中点,
∴OC=BC=2,
在Rt△AOC中,OA==,
∵△ABC绕点O旋转得△A′B'C′,
∴OC′=OC=2,
∵AC′≤OA+OC′(当且仅当点A、O、C′共线时,取等号),
∴AC′的最大值为2+,
即在旋转过程中点A、C′两点间的最大距离是2+.
故答案为2+.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
21、【分析】设AC=x,可知AB=10﹣x,再根据勾股定理即可得出结论.
【解答】解:设AC=x,
∵AC+AB=10,
∴AB=10﹣x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10﹣x)2.
故答案为:x2+32=(10﹣x)2.
【点评】本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
