2018年秋九年级数学上册复习课一1.1-1.3二次函数图象及性质同步测试(新版)浙教版
文档属性
| 名称 | 2018年秋九年级数学上册复习课一1.1-1.3二次函数图象及性质同步测试(新版)浙教版 |  | |
| 格式 | zip | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-09 12:02:27 | ||
图片预览


文档简介
复习课一 (1.1-1.3)
【知识点1】二次函数定义:形如y=ax2+bx+c(a≠0)的函数.
1.若二次函数y=(m-2)x2+m2-4的图象过原点,则m的值为________.
【知识点2】用待定系数法求二次函数的解析式.
2.已知抛物线过A(-2,0),B(1,0)和C(0,2)三点.
(1)求这条抛物线的表达式;
(2)在这条抛物线上是否存在点P,使∠AOP=45°,若存在,请求出点P的坐标;若不存在,请说明理由.
【知识点3】二次函数的增减性与最值.
3.抛物线y=ax2+4x+a-2有最大值为1,则a=________.
4.已知函数y=-x2+bx+c的部分图象如图所示,则b=________,c=________,当x________时,y随x的增大而减小.
第4题图
5.已知抛物线y=-(x+1)2上的两点A(x1,y1)和B(x2,y2),如果x1<x2<-1,那么下列结论一定成立的是( )
A.y1<y2<0 B.0<y1<y2 C.0<y2<y1 D.y2<y1<0
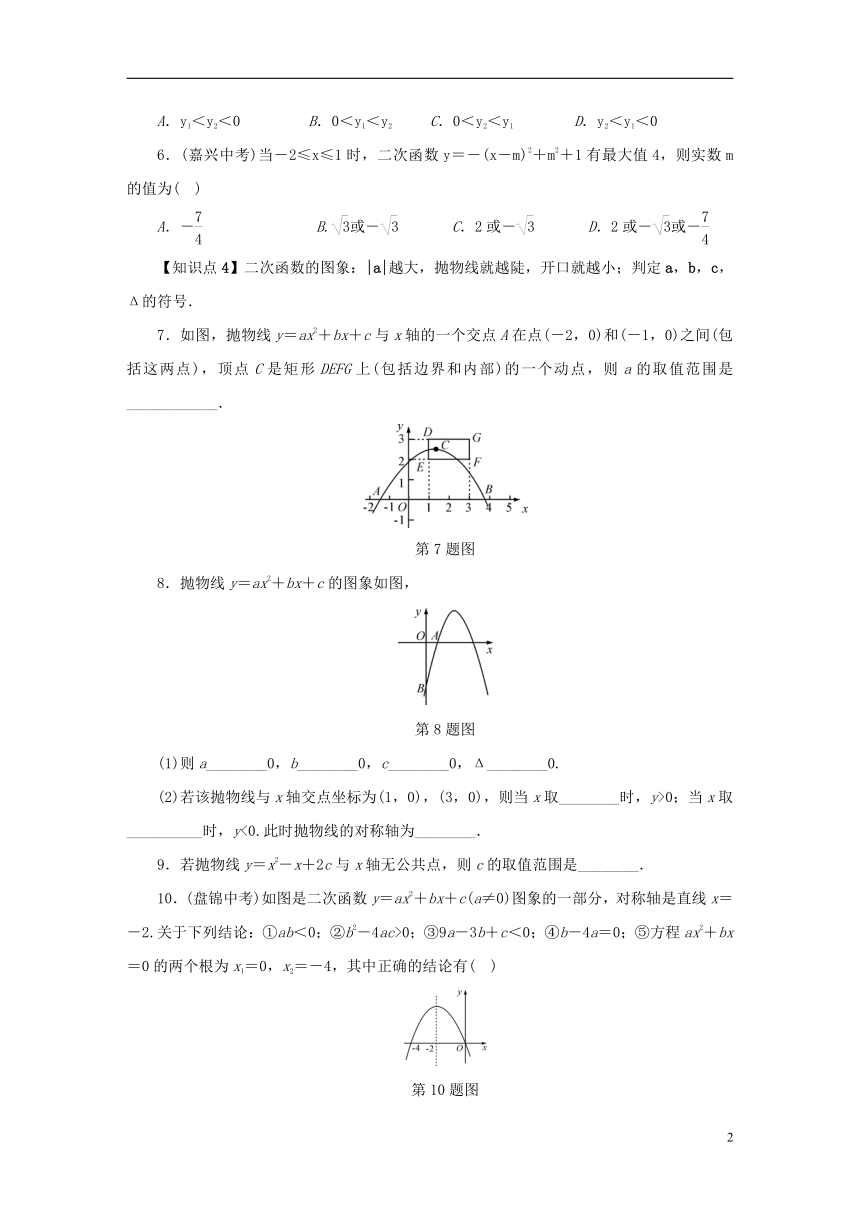
6.(嘉兴中考)当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )
A.- B.或- C.2或- D.2或-或-
【知识点4】二次函数的图象:|a|越大,抛物线就越陡,开口就越小;判定a,b,c,Δ的符号.
7.如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则a的取值范围是____________.
第7题图
抛物线y=ax2+bx+c的图象如图,
第8题图
(1)则a________0,b________0,c________0,Δ________0.
(2)若该抛物线与x轴交点坐标为(1,0),(3,0),则当x取________时,y>0;当x取__________时,y<0.此时抛物线的对称轴为________.
9.若抛物线y=x2-x+2c与x轴无公共点,则c的取值范围是________.
10.(盘锦中考)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
第10题图
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
11.(遵义中考)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图所示,其中正确的是( )
12.(宁波中考)二次函数y=a(x-4)2-4(a≠0)的图象在2A.1 B.-1 C.2 D.-2
13.如图,设抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于C点,点P为该抛物线第四象限上的一点,当△PBC面积最大时,求点P的坐标.
第13题图
14.如图,设抛物线y=x2-2x-3向上平移k(k>0)个单位后所得新抛物线与x轴交于D、E两点,顶点为M点,当k为何值时,△MDE为直角三角形?
第14题图
【知识点5】抛物线的图形变换.
15.将二次函数y=-2(x-1)2-1的图象:①沿x轴翻折得到________________;②沿y轴翻折得到________________;③绕原点旋转180°得到________________.
16.如图1,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).
第16题图
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图2中阴影部分).
复习课一 (1.1-1.3)
-2
2.(1)设抛物线的表达式为y=ax2+bx+c.∵抛物线过A(-2,0),B(1,0)和C(0,2)三点.∴ 解得∴y=-x2-x+2;
第2题图
设存在点P(x,y)使∠AOP=45°,由点A在x轴的负半轴上,点O为原点,可知x<0.如图,过点P作PM⊥AO于点M,由∠POA=45°知,OM=PM,∴当点P在第二象限时,y=-x.由点P在抛物线上,得-x=-x2-x+2,解得x=±(正值舍去).∴x=-,y=-x=,∴点P1.当点P在第三象限时,y=x,得x=-x2-x+2,解得x1=-1(舍去),x2=--1.∴y=x=--1.∴点P2.∴存在点P使∠AOP=45°,点P的坐标为或.
3.-1
4.2 3 ≥1
5-6.AC
7.-≤a≤-
8.(1)< > < > (2)13 直线x=2
9.c>
10-12.BDA
过P作PH⊥x轴于H,交BC于点Q,由题意易求点B坐标为(3,0),点C坐标为(0,-3),∴直线BC的解析式为y=x-3.设P(x,x2-2x-3).则PQ=yQ-yP=(x-3)-(x2-2x-3)=-x2+3x=-+,又S△PBC=×PQ×OB=×PQ,∴当x=时,△PBC面积最大,此时P.
过M作MF⊥x轴于F,则点M(1,-4+k),∵△MDE为直角三角形,∴∠DME=90°,又根据轴对称性,MD=ME,∴MF=EF=DF=4-k,∴E(5-k,0),设新抛物线为y=(x-1)2-4+k,过E(5-k,0),有0=(4-k)2-4+k=(4-k)(3-k),∴k=4(舍去)或k=3,故当k=3时,△MDE为直角三角形.
y=2(x-1)2+1 y=-2(x+1)2-1 y=2(x+1)2+1
16.(1)∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),∴解得∴抛物线的函数表达式为y=x2-4x+3;
第16题图
(2)∵y=x2-4x+3=(x-2)2-1,∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2; (3)如图,∵抛物线的顶点坐标为(2,-1),∴PP′=1,阴影部分的面积等于平行四边形A′APP′的面积,∵平行四边形A′APP′的面积=1×2=2,∴阴影部分的面积S=2.
【知识点1】二次函数定义:形如y=ax2+bx+c(a≠0)的函数.
1.若二次函数y=(m-2)x2+m2-4的图象过原点,则m的值为________.
【知识点2】用待定系数法求二次函数的解析式.
2.已知抛物线过A(-2,0),B(1,0)和C(0,2)三点.
(1)求这条抛物线的表达式;
(2)在这条抛物线上是否存在点P,使∠AOP=45°,若存在,请求出点P的坐标;若不存在,请说明理由.
【知识点3】二次函数的增减性与最值.
3.抛物线y=ax2+4x+a-2有最大值为1,则a=________.
4.已知函数y=-x2+bx+c的部分图象如图所示,则b=________,c=________,当x________时,y随x的增大而减小.
第4题图
5.已知抛物线y=-(x+1)2上的两点A(x1,y1)和B(x2,y2),如果x1<x2<-1,那么下列结论一定成立的是( )
A.y1<y2<0 B.0<y1<y2 C.0<y2<y1 D.y2<y1<0
6.(嘉兴中考)当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )
A.- B.或- C.2或- D.2或-或-
【知识点4】二次函数的图象:|a|越大,抛物线就越陡,开口就越小;判定a,b,c,Δ的符号.
7.如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则a的取值范围是____________.
第7题图
抛物线y=ax2+bx+c的图象如图,
第8题图
(1)则a________0,b________0,c________0,Δ________0.
(2)若该抛物线与x轴交点坐标为(1,0),(3,0),则当x取________时,y>0;当x取__________时,y<0.此时抛物线的对称轴为________.
9.若抛物线y=x2-x+2c与x轴无公共点,则c的取值范围是________.
10.(盘锦中考)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
第10题图
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
11.(遵义中考)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图所示,其中正确的是( )
12.(宁波中考)二次函数y=a(x-4)2-4(a≠0)的图象在2
13.如图,设抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于C点,点P为该抛物线第四象限上的一点,当△PBC面积最大时,求点P的坐标.
第13题图
14.如图,设抛物线y=x2-2x-3向上平移k(k>0)个单位后所得新抛物线与x轴交于D、E两点,顶点为M点,当k为何值时,△MDE为直角三角形?
第14题图
【知识点5】抛物线的图形变换.
15.将二次函数y=-2(x-1)2-1的图象:①沿x轴翻折得到________________;②沿y轴翻折得到________________;③绕原点旋转180°得到________________.
16.如图1,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).
第16题图
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图2中阴影部分).
复习课一 (1.1-1.3)
-2
2.(1)设抛物线的表达式为y=ax2+bx+c.∵抛物线过A(-2,0),B(1,0)和C(0,2)三点.∴ 解得∴y=-x2-x+2;
第2题图
设存在点P(x,y)使∠AOP=45°,由点A在x轴的负半轴上,点O为原点,可知x<0.如图,过点P作PM⊥AO于点M,由∠POA=45°知,OM=PM,∴当点P在第二象限时,y=-x.由点P在抛物线上,得-x=-x2-x+2,解得x=±(正值舍去).∴x=-,y=-x=,∴点P1.当点P在第三象限时,y=x,得x=-x2-x+2,解得x1=-1(舍去),x2=--1.∴y=x=--1.∴点P2.∴存在点P使∠AOP=45°,点P的坐标为或.
3.-1
4.2 3 ≥1
5-6.AC
7.-≤a≤-
8.(1)< > < > (2)1
9.c>
10-12.BDA
过P作PH⊥x轴于H,交BC于点Q,由题意易求点B坐标为(3,0),点C坐标为(0,-3),∴直线BC的解析式为y=x-3.设P(x,x2-2x-3).则PQ=yQ-yP=(x-3)-(x2-2x-3)=-x2+3x=-+,又S△PBC=×PQ×OB=×PQ,∴当x=时,△PBC面积最大,此时P.
过M作MF⊥x轴于F,则点M(1,-4+k),∵△MDE为直角三角形,∴∠DME=90°,又根据轴对称性,MD=ME,∴MF=EF=DF=4-k,∴E(5-k,0),设新抛物线为y=(x-1)2-4+k,过E(5-k,0),有0=(4-k)2-4+k=(4-k)(3-k),∴k=4(舍去)或k=3,故当k=3时,△MDE为直角三角形.
y=2(x-1)2+1 y=-2(x+1)2-1 y=2(x+1)2+1
16.(1)∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),∴解得∴抛物线的函数表达式为y=x2-4x+3;
第16题图
(2)∵y=x2-4x+3=(x-2)2-1,∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2; (3)如图,∵抛物线的顶点坐标为(2,-1),∴PP′=1,阴影部分的面积等于平行四边形A′APP′的面积,∵平行四边形A′APP′的面积=1×2=2,∴阴影部分的面积S=2.
同课章节目录
