2018年秋九年级数学上册复习课二3.1-3.6圆 同步测试(新版)浙教版
文档属性
| 名称 | 2018年秋九年级数学上册复习课二3.1-3.6圆 同步测试(新版)浙教版 | 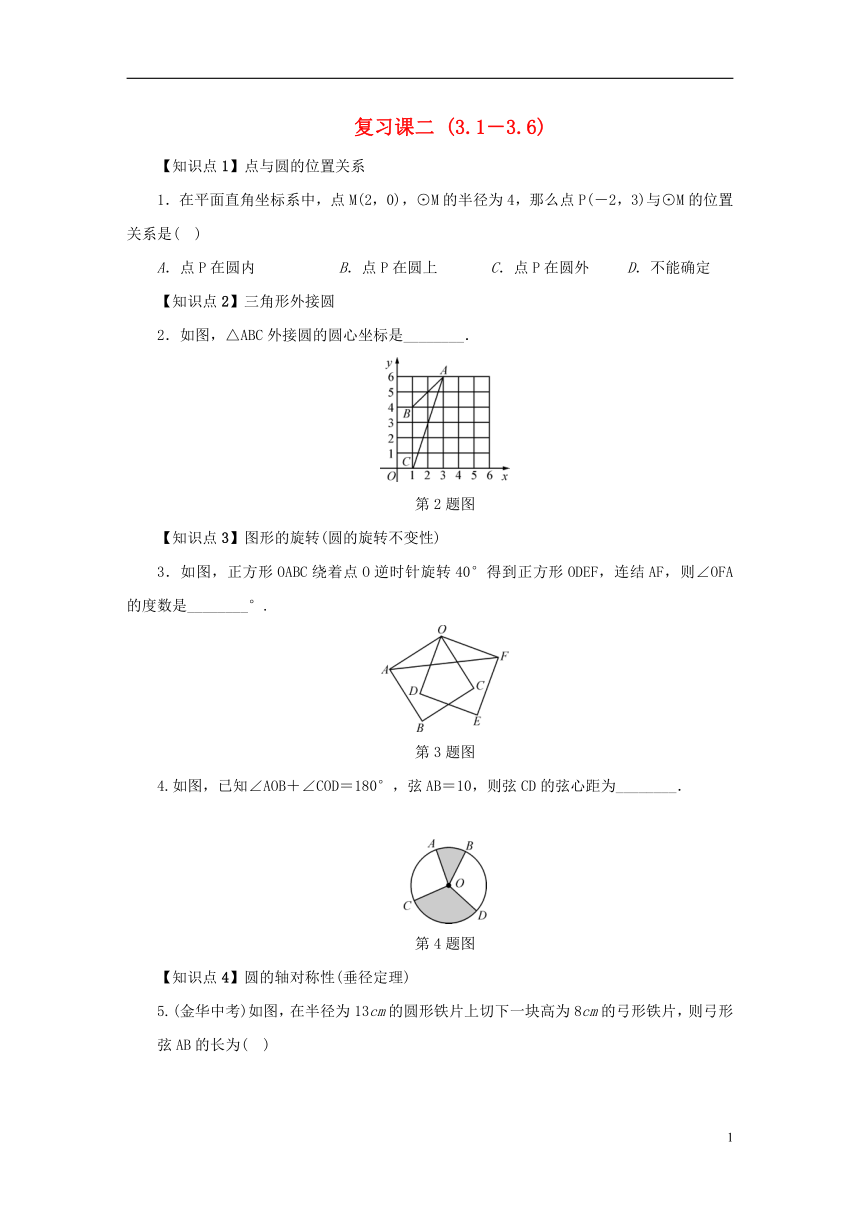 | |
| 格式 | zip | ||
| 文件大小 | 283.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-09 12:08:06 | ||
图片预览



文档简介
复习课二 (3.1-3.6)
【知识点1】点与圆的位置关系
1.在平面直角坐标系中,点M(2,0),⊙M的半径为4,那么点P(-2,3)与⊙M的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
【知识点2】三角形外接圆
2.如图,△ABC外接圆的圆心坐标是________.
第2题图
【知识点3】图形的旋转(圆的旋转不变性)
3.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连结AF,则∠OFA的度数是________°.
第3题图
4.如图,已知∠AOB+∠COD=180°,弦AB=10,则弦CD的弦心距为________.
第4题图
【知识点4】圆的轴对称性(垂径定理)
5.(金华中考)如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
第5题图
A.10cm B.16cm C.24cm D.26cm
6.(陕西中考)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是________.
第6题图
7.如图,已知AB为⊙O的直径且AB=10,弦AC=6,AD平分∠BAC,求AD的长.
第7题图
8.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图1,若BC为⊙O的直径,AB=6,求BD,AD的长;
(2)如图2,若∠CAB=60°,求BD的长.
第8题图
9.(安徽中考)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
第9题图
【知识点5】圆中的角(圆心角,圆周角)
10.(宜昌中考)如图,四边形ABCD内接⊙O,AC平分∠BAD,则下列结论正确的是(B)
A.AB=AD B.BC=CD
C.= D.∠BCA=∠DCA
第10题图
11.(梧州中考)如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连结AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
第11题图
A.20° B.30° C.40° D.70°
(凉山州中考)如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
第12题图
A.80° B.100° C.110° D.130°
13.(兰州中考)已知△ABC的边BC=4cm,⊙O是其外接圆,且半径也为4cm,则∠A的度数是________.
14.(漳州中考)如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为________.
第14题图
15.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB.延长DA与⊙O的另一个交点为E,连结AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长.
第15题图
【知识点6】圆内接四边形
16.(黄石中考)如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
第16题图
A. B. C. D.
17.已知:如图,四边形ABCD内接于⊙O,DB=DC.求证:AD平分∠EAC.
第17题图
复习课二 (3.1-3.6)
1.C 2.(5,2) 3.25 4.5 5.C
6.3
第7题图
连结BC、OD、BD,OD交CB于E,如图,∵AB为半圆O的直径,∴∠ACB=∠ADB=90°,在Rt△ACB中,∵AB=10,AC=6,∴BC==8,∵AD平分∠BAC,∴∠CAD=∠BAD,∴弧CD=弧BD,∴OD垂直平分BC,∴OE=AC=3,BE=BC=4,∴DE=OD-OE=2,在Rt△BDE中,BD==2,在Rt△ADB中,AD==4. 证法二:连结BD并延长交AC的延长线于点G,易证△ADB≌△ADG,由S△ABG=×AG×BC=×BG×AD,求得AD的长. 证法三:连结BD,DC,过D作DM⊥AB于点M,DN⊥AC于点N.易证△BDM≌△CDN,可得AB+AC=2AM=16,∴AM=8,BM=2,OM=3,∴DM=4,AD=4.
(1)如图1,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.∵在直角△CAB中,BC=10,AB=6,∴由勾股定理得到:AC===8.∵AD平分∠CAB,∴=,∴CD=BD.在直角△BDC中,BC=10,CD2+BD2=BC2,∴易得BD=CD=5;过B作BH⊥AD于点H,在△ABH中,AB=6,∠BAD=45°,∴AH=BH=3,在△BDH中,BD=5,BH=3,∴DH=4,∴AD=7. (2)如图2,连结OB,OD.∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=∠CAB=30°,∴∠DOB=2∠DAB=60°.又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5,∴BD=5.
第8题图
9.(1)连结OQ,如图1,∵PQ∥AB,OP⊥PQ,∴OP⊥AB,在Rt△OBP中,∠B=30°,OB=AB=3,易求得OP=,在Rt△OPQ中,∵OP=,OQ=3,∴PQ==; (2)连结OQ,如图2,在Rt△OPQ中,PQ==,当OP的长最小时,PQ的长最大,此时OP⊥BC,则OP=OB=,∴PQ长的最大值为=.
第9题图
10-12.BAD
13.30°或150°
14.61°
(1)∵AB为⊙O的直径,∴∠ACB=90°.∴AC⊥BC.∵DC=CB,∴AD=AB.∴∠B=∠D; (2)设BC=x,则AC=x-2.在Rt△ABC中,AC2+BC2=AB2,∴(x-2)2+x2=42,解得x1=1+,x2=1-(舍去).∵∠B=∠E,∠B=∠D,∴∠D=∠E.∴CD=CE.∵CD=CB,∴CE=CB=1+.
D
证明:∵DB=DC,∴∠DBC=∠DCB,又∠DBC=∠DAC,∠EAD=∠DCB,∴∠EAD=∠DAC,即AD平分∠EAC.
【知识点1】点与圆的位置关系
1.在平面直角坐标系中,点M(2,0),⊙M的半径为4,那么点P(-2,3)与⊙M的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
【知识点2】三角形外接圆
2.如图,△ABC外接圆的圆心坐标是________.
第2题图
【知识点3】图形的旋转(圆的旋转不变性)
3.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连结AF,则∠OFA的度数是________°.
第3题图
4.如图,已知∠AOB+∠COD=180°,弦AB=10,则弦CD的弦心距为________.
第4题图
【知识点4】圆的轴对称性(垂径定理)
5.(金华中考)如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
第5题图
A.10cm B.16cm C.24cm D.26cm
6.(陕西中考)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是________.
第6题图
7.如图,已知AB为⊙O的直径且AB=10,弦AC=6,AD平分∠BAC,求AD的长.
第7题图
8.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图1,若BC为⊙O的直径,AB=6,求BD,AD的长;
(2)如图2,若∠CAB=60°,求BD的长.
第8题图
9.(安徽中考)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
第9题图
【知识点5】圆中的角(圆心角,圆周角)
10.(宜昌中考)如图,四边形ABCD内接⊙O,AC平分∠BAD,则下列结论正确的是(B)
A.AB=AD B.BC=CD
C.= D.∠BCA=∠DCA
第10题图
11.(梧州中考)如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连结AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
第11题图
A.20° B.30° C.40° D.70°
(凉山州中考)如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
第12题图
A.80° B.100° C.110° D.130°
13.(兰州中考)已知△ABC的边BC=4cm,⊙O是其外接圆,且半径也为4cm,则∠A的度数是________.
14.(漳州中考)如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为________.
第14题图
15.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB.延长DA与⊙O的另一个交点为E,连结AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长.
第15题图
【知识点6】圆内接四边形
16.(黄石中考)如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
第16题图
A. B. C. D.
17.已知:如图,四边形ABCD内接于⊙O,DB=DC.求证:AD平分∠EAC.
第17题图
复习课二 (3.1-3.6)
1.C 2.(5,2) 3.25 4.5 5.C
6.3
第7题图
连结BC、OD、BD,OD交CB于E,如图,∵AB为半圆O的直径,∴∠ACB=∠ADB=90°,在Rt△ACB中,∵AB=10,AC=6,∴BC==8,∵AD平分∠BAC,∴∠CAD=∠BAD,∴弧CD=弧BD,∴OD垂直平分BC,∴OE=AC=3,BE=BC=4,∴DE=OD-OE=2,在Rt△BDE中,BD==2,在Rt△ADB中,AD==4. 证法二:连结BD并延长交AC的延长线于点G,易证△ADB≌△ADG,由S△ABG=×AG×BC=×BG×AD,求得AD的长. 证法三:连结BD,DC,过D作DM⊥AB于点M,DN⊥AC于点N.易证△BDM≌△CDN,可得AB+AC=2AM=16,∴AM=8,BM=2,OM=3,∴DM=4,AD=4.
(1)如图1,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.∵在直角△CAB中,BC=10,AB=6,∴由勾股定理得到:AC===8.∵AD平分∠CAB,∴=,∴CD=BD.在直角△BDC中,BC=10,CD2+BD2=BC2,∴易得BD=CD=5;过B作BH⊥AD于点H,在△ABH中,AB=6,∠BAD=45°,∴AH=BH=3,在△BDH中,BD=5,BH=3,∴DH=4,∴AD=7. (2)如图2,连结OB,OD.∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=∠CAB=30°,∴∠DOB=2∠DAB=60°.又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5,∴BD=5.
第8题图
9.(1)连结OQ,如图1,∵PQ∥AB,OP⊥PQ,∴OP⊥AB,在Rt△OBP中,∠B=30°,OB=AB=3,易求得OP=,在Rt△OPQ中,∵OP=,OQ=3,∴PQ==; (2)连结OQ,如图2,在Rt△OPQ中,PQ==,当OP的长最小时,PQ的长最大,此时OP⊥BC,则OP=OB=,∴PQ长的最大值为=.
第9题图
10-12.BAD
13.30°或150°
14.61°
(1)∵AB为⊙O的直径,∴∠ACB=90°.∴AC⊥BC.∵DC=CB,∴AD=AB.∴∠B=∠D; (2)设BC=x,则AC=x-2.在Rt△ABC中,AC2+BC2=AB2,∴(x-2)2+x2=42,解得x1=1+,x2=1-(舍去).∵∠B=∠E,∠B=∠D,∴∠D=∠E.∴CD=CE.∵CD=CB,∴CE=CB=1+.
D
证明:∵DB=DC,∴∠DBC=∠DCB,又∠DBC=∠DAC,∠EAD=∠DCB,∴∠EAD=∠DAC,即AD平分∠EAC.
同课章节目录
