4.4相似三角形的判定(2)课件(12张PPT)
文档属性
| 名称 | 4.4相似三角形的判定(2)课件(12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 314.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-14 16:00:05 | ||
图片预览




文档简介
浙教版九年级上册
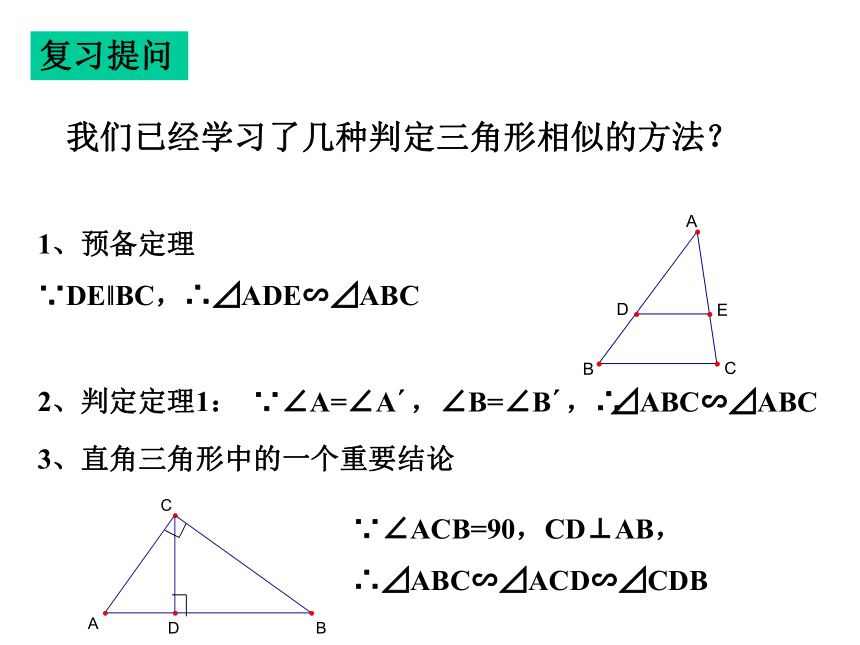
复习提问
我们已经学习了几种判定三角形相似的方法?
下面我们来探究还可用哪些条件来判定两个三角形相似?
我们学习了三角形相似的判定定理1,类似于三角形全等的“SAS” 、“SSS”判定方法,三角形相似还有两个判定方法,即判定定理2和判定定理3。
合作学习:P109--110
讲解新课
判定定理2: “两边对应成比例,且夹角相等的两三角形相似”
已知:如图,△A?B?C?和△ABC中, ∠A?=∠A,A?B?:AB=A?C?:AC
求证:△A?B?C?∽△ABC
判定定理2的符号语言:
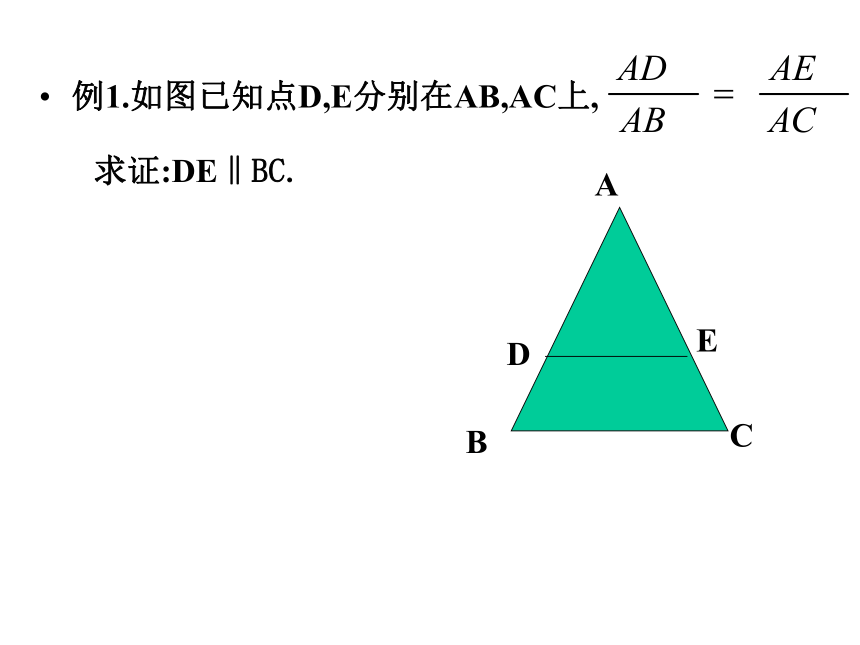
例1.如图已知点D,E分别在AB,AC上,
求证:DE‖BC.
A
B
C
D
E
例2
如图是用卡钳测量容器内径的示意图.现量得卡钳AD两端点的距离为5厘米,且AO/BO=DO/CO=1/2.
求容器的内径BC.
D
A
B
C
O
判定定理3: 三边对应成比例,两三角形相似。
判定定理3的几何格式:
例3.如图判断4×4方格中的两个三角形是否相似,并说明理由.
E
D
F
B
A
C
例4
已知:如图,O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且OD/OA=OE/OB=OF/OC.
求证:△DEF∽△ABC.
A
B
C
O
D
E
F
例3
依据下列各组条件,判定△ABC与△A?B?C?是
不是相似,并说明为什么:
⑴∠A=120?,AB=7厘米,AC=14厘米,
∠A?=120?,A?B?=3厘米,A?C?=6厘米;
⑵AB=4厘米,BC=6厘米,AC=8厘米,
A?B?=12厘米,B?C?=18厘米,A?C?=24厘米
在有平行横线的练习薄上画一条线段AB,使线段A,B恰好在两条平行线上,线段AB就被平行线分成了相等的三小段,你能说出这一事实的数学原理吗?如果只给你圆规和直尺,你会把任意一条线段AB五等分吗?请试一试,并说明你的画法的依据.
结束寄语
不经历风雨,怎么见彩虹.,没有人能随随便便成功!
复习提问
我们已经学习了几种判定三角形相似的方法?
下面我们来探究还可用哪些条件来判定两个三角形相似?
我们学习了三角形相似的判定定理1,类似于三角形全等的“SAS” 、“SSS”判定方法,三角形相似还有两个判定方法,即判定定理2和判定定理3。
合作学习:P109--110
讲解新课
判定定理2: “两边对应成比例,且夹角相等的两三角形相似”
已知:如图,△A?B?C?和△ABC中, ∠A?=∠A,A?B?:AB=A?C?:AC
求证:△A?B?C?∽△ABC
判定定理2的符号语言:
例1.如图已知点D,E分别在AB,AC上,
求证:DE‖BC.
A
B
C
D
E
例2
如图是用卡钳测量容器内径的示意图.现量得卡钳AD两端点的距离为5厘米,且AO/BO=DO/CO=1/2.
求容器的内径BC.
D
A
B
C
O
判定定理3: 三边对应成比例,两三角形相似。
判定定理3的几何格式:
例3.如图判断4×4方格中的两个三角形是否相似,并说明理由.
E
D
F
B
A
C
例4
已知:如图,O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且OD/OA=OE/OB=OF/OC.
求证:△DEF∽△ABC.
A
B
C
O
D
E
F
例3
依据下列各组条件,判定△ABC与△A?B?C?是
不是相似,并说明为什么:
⑴∠A=120?,AB=7厘米,AC=14厘米,
∠A?=120?,A?B?=3厘米,A?C?=6厘米;
⑵AB=4厘米,BC=6厘米,AC=8厘米,
A?B?=12厘米,B?C?=18厘米,A?C?=24厘米
在有平行横线的练习薄上画一条线段AB,使线段A,B恰好在两条平行线上,线段AB就被平行线分成了相等的三小段,你能说出这一事实的数学原理吗?如果只给你圆规和直尺,你会把任意一条线段AB五等分吗?请试一试,并说明你的画法的依据.
结束寄语
不经历风雨,怎么见彩虹.,没有人能随随便便成功!
同课章节目录
