浙教版九上 圆(3.1-3.4)较难题专练【解析版】
文档属性
| 名称 | 浙教版九上 圆(3.1-3.4)较难题专练【解析版】 | 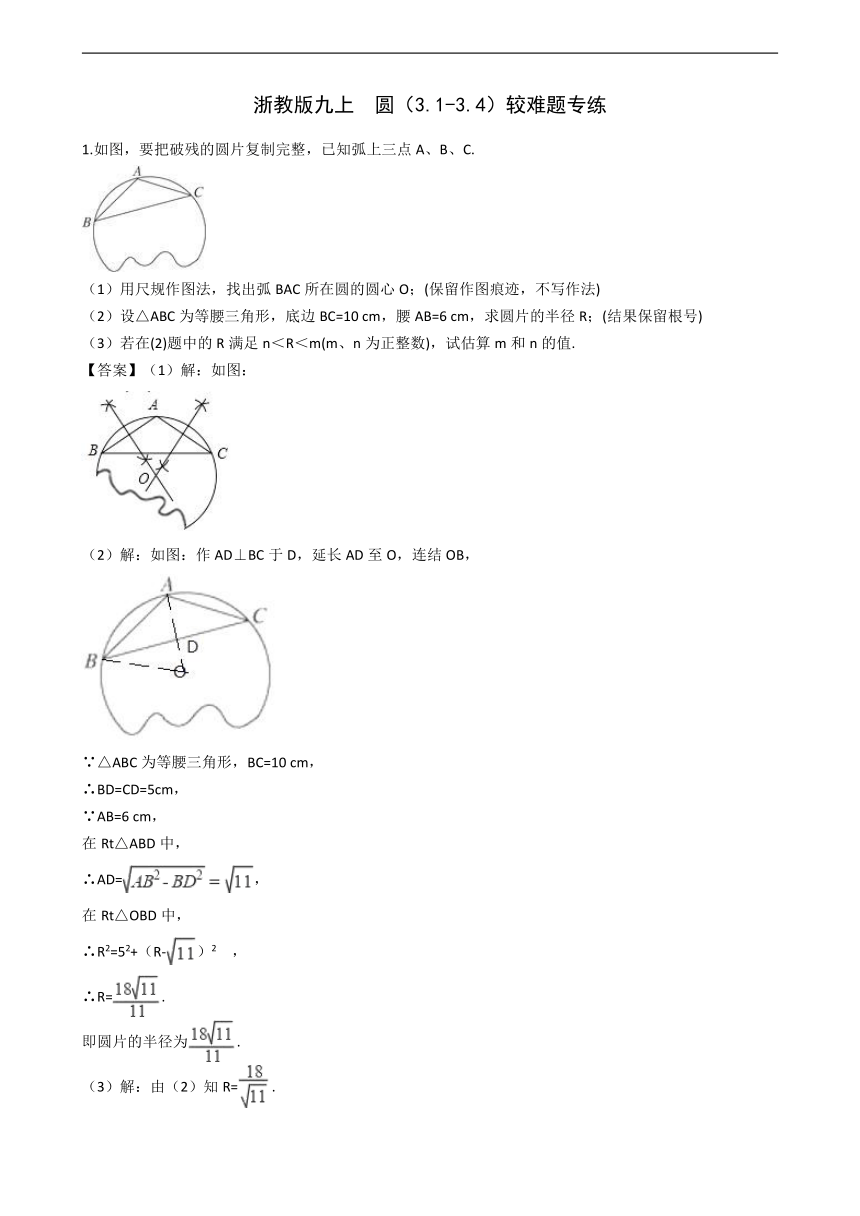 | |
| 格式 | zip | ||
| 文件大小 | 194.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-21 19:01:56 | ||
图片预览





文档简介
浙教版九上 圆(3.1-3.4)较难题专练
1.如图,要把破残的圆片复制完整,已知弧上三点A、B、C.
(1)用尺规作图法,找出弧BAC所在圆的圆心O;(保留作图痕迹,不写作法)
(2)设△ABC为等腰三角形,底边BC=10 cm,腰AB=6 cm,求圆片的半径R;(结果保留根号)
(3)若在(2)题中的R满足n<R<m(m、n为正整数),试估算m和n的值.
【答案】(1)解:如图: (2)解:如图:作AD⊥BC于D,延长AD至O,连结OB, ∵△ABC为等腰三角形,BC=10 cm, ∴BD=CD=5cm, ∵AB=6 cm, 在Rt△ABD中, ∴AD=, 在Rt△OBD中, ∴R2=52+(R-)2 , ∴R=. 即圆片的半径为. (3)解:由(2)知R=. ∵3<<4, ∴4.5<<6, 又∵n<R<m, ∴n=5,m=6
【考点】垂径定理的应用,作图—基本作图
【解析】【分析】(1)作出AB、AC的垂直平分线,交点即为圆心O. (2)作AD⊥BC于D,延长AD至O,连结OB,根据等腰三角形的性质和垂径定理可知BD=CD=5cm,在Rt△ABD中,由勾股定理求得AD;在Rt△OBD中,由勾股定理求得半径R. (3)由3<<4,从而估算的范围,从而得出m、n的值.
2.????????????????????????????????????????????????????????????
(1)问题提出 如图1,点A为线段BC外一动点,且 ,填空:当点A位于________时,线段AC的长取得最大值,且最大值为________ 用含 的式子表示 .
(2)问题探究 点A为线段BC外一动点,且 ,如图2所示,分别以 为边,作等边三角形ABD和等边三角形ACE,连接 ,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
(3)问题解决: ①如图3,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,点P为线段AB外一动点,且 ,求线段AM长的最大值及此时点P的坐标. 如图4,在四边形ABCD中, ,若对角线 于点D,请直接写出对角线AC的最大值.
【答案】(1)CB的延长线上; (2)解: , 理由:∵ 与 是等边三角形, ∴ , ∴ , 即 , 在 与 中, , ∴ ≌ , ∴ ; ②∵线段BE长的最大值 线段CD的最大值, ∴由 知,当线段CD的长取得最大值时,点D在CB的延长线上, ∴最大值为 (3)解:①如图5,连接BM,将 绕着点P顺时针旋转 得到 ,连接AN,则 是等腰直角三角形, ∴ , ∵ 的坐标为 ,点B的坐标为 , ∴ , ∴ , ∴线段AM长的最大值 线段BN长的最大值, ∴当N在线段BA的延长线时,线段BN取得最大值, 最大值 , ∵ , ∴最大值为 ; 如图6,过P作 轴于E, ∵ 是等腰直角三角形, ∴ , ∴ , ∴ ? ②如下图7,以BC为边作等边三角形△BCM,连接DM, ∵ , ∴ ∵ , ∴ ≌ , ∴ , ∴欲求AC的最大值,只要求出DM的最大值即可, ∵ 定值, , ∴点D在以BC为直径的 上运动, 由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=等腰直角△BDC斜边上的高+等边△BCM的高, ∵BC= , ∴DM最大= , ∴AC最大=
【考点】三角形三边关系,全等三角形的判定与性质,等边三角形的判定与性质,三角形的外接圆与外心
【解析】【解答】解:(1)∵点A为线段BC外一动点,且 , ∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为 , 故答案为:CB的延长线上, ; 【分析】(1)由三角形三边关系定理可知,三角形任意两边之和大于第三边,当点A在CB的延长线上时,两边之和等于第三边,所以当点A在CB的延长线上时,线段AC的长取得最大值,且最大值为a+b; (2)根据等边三角形的性质用边角边易证得△CAD≌△EAB,则BE=CD;由(1)中的结论可得BE的最大值=AB+AE; (3)①根据已知条件PM=PB可将△APM绕着点P顺时针旋转90度 得到△PBN,连接AN,BM,由旋转的性质可求解; ②由题意可作辅助线,以BC为边作等边三角形△BCM,连接DM,并作出三角形BCD的外接圆,用边角边易证得△ABC≌△DBM,则AC=DM,要求AC的最大值,只要求出DM的最大值即可,由圆的性质可知,当DM过圆心时,DM最大,即由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,且最大值=等腰直角△BDC斜边上的高+等边△BCM的高。
3.如图①,将一个边长为2的正方形ABCD和一个长为2,宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图②,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能,说明理由.
【答案】(1)解:∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴CE=CH=1,∴△CEH为等腰直角三角形,∴∠ECH=45°,∴∠α=30° (2)证明:∵G为BC中点,∴CG=1,∴CG=CE,∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴∠D′CE′=∠DCE=90°,CE=CE′=CG,∴∠GCD′=∠DCE′=90°+α,在△GCD′和△E′CD中,∵CD′=CD,∠GCD=∠DCE′,CG=CE′,∴△GCD′≌△E′CD(SAS),∴GD′=E′D (3)解:能. 理由如下: ∵四边形ABCD为正方形,∴CB=CD,∵CD′=CD′,∴△BCD′与△DCD′为腰相等的两等腰三角形,当∠BCD′=∠DCD′时,△BCD′≌△DCD′,当△BCD′与△DCD′为钝角三角形时,则旋转角α=(360°-90°)÷2=135°,当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′= ∠BCD=45°,则α=360°﹣90°÷2=315°,即旋转角a的值为135°或315°时,△BCD′与△DCD′全等
【考点】三角形全等的判定,等腰三角形的性质,正方形的性质,旋转的性质
【解析】【分析】(1)根据旋转的性质对应边不变,得出等腰直角三角形,再求出∠α。(2)根据旋转前后的两个图形全等,边角相等,再利用三角形全等得出边对应相等。(3)根据三角形全等,旋转的性质进行判断.
4.如图,在平面直角坐标系中,已知A(﹣2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.
(1)求点O′的坐标;
(2)已知抛物线y=ax2+bx+c过A,B,C三点,且与⊙O′交于另一点E,求抛物线的解析式,并直接写出点E 坐标;
(3)设点P(t,0)是线段OB上一个动点,过点P作直线l⊥x轴,交线段BC于F,交抛物线y=ax2+bx+c于点G,请用t表示四边形BPCG的面积S;
(4)在(3)的条件下,四边形BPCG能否为平行四边形?若能,请求出t的值;若不能,请说明理由.
【答案】(1)解:如图1中,连接CO′,设⊙O′的半径为R. 在Rt△OCO′中,∵OC2+OO2=CO′2 , ∴42+(R﹣2)2=R2 , ∴R=5, ∴OO′=5﹣2=3, ∴O′(3,0). (2)解:∵A(﹣2,0),C(0,4),B(8,0), ∴ ,解得 , ∴抛物线的解析式为y=﹣ x2+ x+4. 易知E、C关于对称轴对称, ∴点E的纵坐标为4, ∴E(6,4) (3)解:由题意G(t,﹣ t2+ t+4), ∴S四边形BPCG= ?PG?(Bx﹣Cx)= ?(﹣ t2+ t+4)?8=﹣t2+6t+16(0<t<8) (4)解:不可能是平行四边形. 理由:假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB﹣OP=2, ∴CE≠BP, ∴四边形BPCG不可能是平行四边形.
【考点】勾股定理,平行四边形的判定与性质,圆心角、弧、弦的关系
【解析】【分析】(1)如图1中,连接CO′,设⊙O′的半径为R.在Rt△OCO′中,根据OC2+OO2=CO′2 , 可得42+(R-2)2=R2 , 解方程求出求点O′的坐标; (2)把A(-2,0),C(0,4),B(8,0)代入抛物线抛物线y=ax2+bx+c,求抛物线的解析式即点E 坐标; (3)根据S四边形BPCG=?PG?(Bx-Cx),即可用t表示四边形BPCG的面积S (4)不可能是平行四边形.假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB-OP=2,推出CE≠BP,即可得到所求结论..
5.问题提出
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于________时,线段AC的长取得最大值,且最大值为________(用含a,b的式子表示).
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
(3)如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(4)如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC= ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
【答案】(1)CB延长线上;a+b 问题探究 (2)解:①CD=BE,理由:∵△ABD与△ACE是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.在△CAD与△EAB中, ,∴△CAD≌△EAB(SAS),∴CD=BE; ②∵线段BE长的最大值=线段CD的最大值,∴由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,∴最大值为BD+BC=AB+BC=3+6=9; 问题解决: (3)解:如图1,连接BM. ∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=2,BN=AM.∵A的坐标为(2,0),点B的坐标为(5,0),∴OA=2,OB=5,∴AB=3,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN.∵AN= AP=2 ,∴最大值为2 +3; 如图2,过P作PE⊥x轴于E. ∵△APN是等腰直角三角形,∴PE=AE= ,∴OE=BO﹣AB﹣AE=5﹣3﹣ =2﹣ ,∴P(2﹣ ). (4)解:如图4中, 以BC为边作等边三角形△BCM.∵∠ABD=∠CBM=60°,∴∠ABC=∠DBM.∵AB=DB,BC=BM,∴△ABC≌△DBM,∴AC=MD,∴欲求AC的最大值,只要求出DM的最大值即可.∵BC=4 =定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2 +2 ,∴AC的最大值为2 +2 .
【考点】全等三角形的判定与性质,等边三角形的判定与性质,旋转的性质
【解析】【解答】(1)解:∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b. 【分析】(1)由线段的构成可知,当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b; (2)①CD=BE,理由:由等边三角形的性质可得AD=AB,AC=AE,∠BAD=∠CAE=60°,所以∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.在△CAD与△EAB中,用边角边可证得△CAD≌△EAB(SAS),所以CD=BE; ②由①得,CD=BE,所以线段BE长的最大值=线段CD的最大值,由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,所以线段BE长的最大值为BD+BC=AB+BC=3+6=9; (3)如图1,连接BM.因为PM=PB,所以将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,由旋转的性质可得△APN是等腰直角三角形,所以PN=PA=2,BN=AM.而已知A的坐标为(2,0),点B的坐标为(5,0),所以OA=2,OB=5,则AB=OB-OA=3,所以线段AM长的最大值=线段BN长的最大值,由(1)知,当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN.因为AN=2AP=2,∴最大值为2+3; 如图2,过P作PE⊥x轴于E.根据等腰直角三角形的性质可得PE=AE=,OE=BO﹣AB﹣AE=5﹣3-=2-,所以P(2-,); (4)以BC为边作等边三角形△BCM.由等边三角形的性质可得∠ABD=∠CBM=60°,所以∠ABD+∠DBC=∠CBM+∠DBC,即∠ABC=∠DBM,用边角边可证得△ABC≌△DBM,所以AC=MD,而当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2+2,所以AC的最大值为2+2.
1.如图,要把破残的圆片复制完整,已知弧上三点A、B、C.
(1)用尺规作图法,找出弧BAC所在圆的圆心O;(保留作图痕迹,不写作法)
(2)设△ABC为等腰三角形,底边BC=10 cm,腰AB=6 cm,求圆片的半径R;(结果保留根号)
(3)若在(2)题中的R满足n<R<m(m、n为正整数),试估算m和n的值.
【答案】(1)解:如图: (2)解:如图:作AD⊥BC于D,延长AD至O,连结OB, ∵△ABC为等腰三角形,BC=10 cm, ∴BD=CD=5cm, ∵AB=6 cm, 在Rt△ABD中, ∴AD=, 在Rt△OBD中, ∴R2=52+(R-)2 , ∴R=. 即圆片的半径为. (3)解:由(2)知R=. ∵3<<4, ∴4.5<<6, 又∵n<R<m, ∴n=5,m=6
【考点】垂径定理的应用,作图—基本作图
【解析】【分析】(1)作出AB、AC的垂直平分线,交点即为圆心O. (2)作AD⊥BC于D,延长AD至O,连结OB,根据等腰三角形的性质和垂径定理可知BD=CD=5cm,在Rt△ABD中,由勾股定理求得AD;在Rt△OBD中,由勾股定理求得半径R. (3)由3<<4,从而估算的范围,从而得出m、n的值.
2.????????????????????????????????????????????????????????????
(1)问题提出 如图1,点A为线段BC外一动点,且 ,填空:当点A位于________时,线段AC的长取得最大值,且最大值为________ 用含 的式子表示 .
(2)问题探究 点A为线段BC外一动点,且 ,如图2所示,分别以 为边,作等边三角形ABD和等边三角形ACE,连接 ,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
(3)问题解决: ①如图3,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,点P为线段AB外一动点,且 ,求线段AM长的最大值及此时点P的坐标. 如图4,在四边形ABCD中, ,若对角线 于点D,请直接写出对角线AC的最大值.
【答案】(1)CB的延长线上; (2)解: , 理由:∵ 与 是等边三角形, ∴ , ∴ , 即 , 在 与 中, , ∴ ≌ , ∴ ; ②∵线段BE长的最大值 线段CD的最大值, ∴由 知,当线段CD的长取得最大值时,点D在CB的延长线上, ∴最大值为 (3)解:①如图5,连接BM,将 绕着点P顺时针旋转 得到 ,连接AN,则 是等腰直角三角形, ∴ , ∵ 的坐标为 ,点B的坐标为 , ∴ , ∴ , ∴线段AM长的最大值 线段BN长的最大值, ∴当N在线段BA的延长线时,线段BN取得最大值, 最大值 , ∵ , ∴最大值为 ; 如图6,过P作 轴于E, ∵ 是等腰直角三角形, ∴ , ∴ , ∴ ? ②如下图7,以BC为边作等边三角形△BCM,连接DM, ∵ , ∴ ∵ , ∴ ≌ , ∴ , ∴欲求AC的最大值,只要求出DM的最大值即可, ∵ 定值, , ∴点D在以BC为直径的 上运动, 由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=等腰直角△BDC斜边上的高+等边△BCM的高, ∵BC= , ∴DM最大= , ∴AC最大=
【考点】三角形三边关系,全等三角形的判定与性质,等边三角形的判定与性质,三角形的外接圆与外心
【解析】【解答】解:(1)∵点A为线段BC外一动点,且 , ∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为 , 故答案为:CB的延长线上, ; 【分析】(1)由三角形三边关系定理可知,三角形任意两边之和大于第三边,当点A在CB的延长线上时,两边之和等于第三边,所以当点A在CB的延长线上时,线段AC的长取得最大值,且最大值为a+b; (2)根据等边三角形的性质用边角边易证得△CAD≌△EAB,则BE=CD;由(1)中的结论可得BE的最大值=AB+AE; (3)①根据已知条件PM=PB可将△APM绕着点P顺时针旋转90度 得到△PBN,连接AN,BM,由旋转的性质可求解; ②由题意可作辅助线,以BC为边作等边三角形△BCM,连接DM,并作出三角形BCD的外接圆,用边角边易证得△ABC≌△DBM,则AC=DM,要求AC的最大值,只要求出DM的最大值即可,由圆的性质可知,当DM过圆心时,DM最大,即由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,且最大值=等腰直角△BDC斜边上的高+等边△BCM的高。
3.如图①,将一个边长为2的正方形ABCD和一个长为2,宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图②,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能,说明理由.
【答案】(1)解:∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴CE=CH=1,∴△CEH为等腰直角三角形,∴∠ECH=45°,∴∠α=30° (2)证明:∵G为BC中点,∴CG=1,∴CG=CE,∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴∠D′CE′=∠DCE=90°,CE=CE′=CG,∴∠GCD′=∠DCE′=90°+α,在△GCD′和△E′CD中,∵CD′=CD,∠GCD=∠DCE′,CG=CE′,∴△GCD′≌△E′CD(SAS),∴GD′=E′D (3)解:能. 理由如下: ∵四边形ABCD为正方形,∴CB=CD,∵CD′=CD′,∴△BCD′与△DCD′为腰相等的两等腰三角形,当∠BCD′=∠DCD′时,△BCD′≌△DCD′,当△BCD′与△DCD′为钝角三角形时,则旋转角α=(360°-90°)÷2=135°,当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′= ∠BCD=45°,则α=360°﹣90°÷2=315°,即旋转角a的值为135°或315°时,△BCD′与△DCD′全等
【考点】三角形全等的判定,等腰三角形的性质,正方形的性质,旋转的性质
【解析】【分析】(1)根据旋转的性质对应边不变,得出等腰直角三角形,再求出∠α。(2)根据旋转前后的两个图形全等,边角相等,再利用三角形全等得出边对应相等。(3)根据三角形全等,旋转的性质进行判断.
4.如图,在平面直角坐标系中,已知A(﹣2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.
(1)求点O′的坐标;
(2)已知抛物线y=ax2+bx+c过A,B,C三点,且与⊙O′交于另一点E,求抛物线的解析式,并直接写出点E 坐标;
(3)设点P(t,0)是线段OB上一个动点,过点P作直线l⊥x轴,交线段BC于F,交抛物线y=ax2+bx+c于点G,请用t表示四边形BPCG的面积S;
(4)在(3)的条件下,四边形BPCG能否为平行四边形?若能,请求出t的值;若不能,请说明理由.
【答案】(1)解:如图1中,连接CO′,设⊙O′的半径为R. 在Rt△OCO′中,∵OC2+OO2=CO′2 , ∴42+(R﹣2)2=R2 , ∴R=5, ∴OO′=5﹣2=3, ∴O′(3,0). (2)解:∵A(﹣2,0),C(0,4),B(8,0), ∴ ,解得 , ∴抛物线的解析式为y=﹣ x2+ x+4. 易知E、C关于对称轴对称, ∴点E的纵坐标为4, ∴E(6,4) (3)解:由题意G(t,﹣ t2+ t+4), ∴S四边形BPCG= ?PG?(Bx﹣Cx)= ?(﹣ t2+ t+4)?8=﹣t2+6t+16(0<t<8) (4)解:不可能是平行四边形. 理由:假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB﹣OP=2, ∴CE≠BP, ∴四边形BPCG不可能是平行四边形.
【考点】勾股定理,平行四边形的判定与性质,圆心角、弧、弦的关系
【解析】【分析】(1)如图1中,连接CO′,设⊙O′的半径为R.在Rt△OCO′中,根据OC2+OO2=CO′2 , 可得42+(R-2)2=R2 , 解方程求出求点O′的坐标; (2)把A(-2,0),C(0,4),B(8,0)代入抛物线抛物线y=ax2+bx+c,求抛物线的解析式即点E 坐标; (3)根据S四边形BPCG=?PG?(Bx-Cx),即可用t表示四边形BPCG的面积S (4)不可能是平行四边形.假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB-OP=2,推出CE≠BP,即可得到所求结论..
5.问题提出
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于________时,线段AC的长取得最大值,且最大值为________(用含a,b的式子表示).
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
(3)如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(4)如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC= ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
【答案】(1)CB延长线上;a+b 问题探究 (2)解:①CD=BE,理由:∵△ABD与△ACE是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.在△CAD与△EAB中, ,∴△CAD≌△EAB(SAS),∴CD=BE; ②∵线段BE长的最大值=线段CD的最大值,∴由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,∴最大值为BD+BC=AB+BC=3+6=9; 问题解决: (3)解:如图1,连接BM. ∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=2,BN=AM.∵A的坐标为(2,0),点B的坐标为(5,0),∴OA=2,OB=5,∴AB=3,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN.∵AN= AP=2 ,∴最大值为2 +3; 如图2,过P作PE⊥x轴于E. ∵△APN是等腰直角三角形,∴PE=AE= ,∴OE=BO﹣AB﹣AE=5﹣3﹣ =2﹣ ,∴P(2﹣ ). (4)解:如图4中, 以BC为边作等边三角形△BCM.∵∠ABD=∠CBM=60°,∴∠ABC=∠DBM.∵AB=DB,BC=BM,∴△ABC≌△DBM,∴AC=MD,∴欲求AC的最大值,只要求出DM的最大值即可.∵BC=4 =定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2 +2 ,∴AC的最大值为2 +2 .
【考点】全等三角形的判定与性质,等边三角形的判定与性质,旋转的性质
【解析】【解答】(1)解:∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b. 【分析】(1)由线段的构成可知,当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b; (2)①CD=BE,理由:由等边三角形的性质可得AD=AB,AC=AE,∠BAD=∠CAE=60°,所以∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.在△CAD与△EAB中,用边角边可证得△CAD≌△EAB(SAS),所以CD=BE; ②由①得,CD=BE,所以线段BE长的最大值=线段CD的最大值,由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,所以线段BE长的最大值为BD+BC=AB+BC=3+6=9; (3)如图1,连接BM.因为PM=PB,所以将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,由旋转的性质可得△APN是等腰直角三角形,所以PN=PA=2,BN=AM.而已知A的坐标为(2,0),点B的坐标为(5,0),所以OA=2,OB=5,则AB=OB-OA=3,所以线段AM长的最大值=线段BN长的最大值,由(1)知,当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN.因为AN=2AP=2,∴最大值为2+3; 如图2,过P作PE⊥x轴于E.根据等腰直角三角形的性质可得PE=AE=,OE=BO﹣AB﹣AE=5﹣3-=2-,所以P(2-,); (4)以BC为边作等边三角形△BCM.由等边三角形的性质可得∠ABD=∠CBM=60°,所以∠ABD+∠DBC=∠CBM+∠DBC,即∠ABC=∠DBM,用边角边可证得△ABC≌△DBM,所以AC=MD,而当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2+2,所以AC的最大值为2+2.
同课章节目录
