4.2 平面直角坐标系(1)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 4.2 平面直角坐标系(1)(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 374.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-27 00:00:00 | ||
图片预览


文档简介
浙江版八年级数学上册第4章图形与坐标4.2平面直角坐标系
第1课时 平面直角坐标系(1)
【知识清单】
一、平面直角坐标系的含义及有关概念:
1. 平面直角坐标系有关概念:如图1,在平面内画两条互相垂直且有公共原点O的数轴,其中一条(通常画成水平的)叫做x轴或横轴,向右的方向为正方向;另一条(画成与x轴垂直的)叫做y轴或纵轴,向上的方向为正方向.这样就在平面内建立了平面直角坐标系,简称坐标系.坐标系所在的平面就叫做坐标平面,两坐标轴的公共原点O叫做直角坐标系的原点.?
2.点的坐标确定方法:如图2,对于平面内任意一点M,过M作MM1⊥x轴、MM2⊥y轴,设垂足M1,M2在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序实数对(x,y)叫做M点的坐标.??规定点的坐标用(x,y)表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒.
3.在直角坐标系中如何根据点的坐标找出这个点:如图3,如点P的坐标为(a,b),?在x轴上找到坐标为a的点A,过A作x轴的垂线,再在y轴上找到坐标为b的点B,过B作y轴的垂线,两垂线的交点即为所找的P点.??[来源:学科网ZXXK]
二、平面直角坐标系的象限的划分及象限中点的坐标符号的确定:如图4.?
? 1.象限划分:x轴和y轴把坐标平面分成四个象限,规定两条数轴的正方向的所夹的象限叫做第一象限,其它三个象限按逆时针方向依次叫做第二象限;第三象限;第四象限.坐标轴上的点不属于任何象限;
2.象限中点的坐标的符号的确定:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)?.若点P(x, y)在第一象限?x>0,y>0;点P(x, y)在第二象限?x<0,y>0;
点P(x, y)在第三象限?x<0,y<0;点P(x, y)在第四象限?x>0,y<0.
3.x轴,y轴上点的坐标的特征:点P(x, y)在x轴上?y为0(点纵坐标为0),x为任意实数,一般表示为P(x,0);点P(x,y)在y轴上?x为0(点横坐标为0),y为任意实数,一般表示为P(0,y).
三、点P(x, y)坐标的几何意义:
1.点P(x, y)到x轴的距离是;2.点P(x, y)到y袖的距离是;3. 点P(x, y)到原点的距离等于.
四、坐标与有序实数对的关系:
在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与之对应;反过来,对于任意一个有序实数对,在平面内都有的一点与它对应.
五、注意:
1. 有序实数对意义:(1)a与b要用逗号分开,以示它们是两个独立有序的数,又要用括号“包装”起来,表示它们是一个整体;(2)若a≠b则(a,b)与(b,a)表示两个不同的有序数对;(3)在直角坐标系中,有序数对(a,b)表示点的坐标,a,b依次表示横坐标、纵坐标.切记横坐标在前,坐标标在后.
2.组成平面直角坐标系的四个要素:①在同一平面内;②两条数轴;③互相垂直;④有公共原点.
3.两个规定:①正方向的规定:横轴取向右为正方向,纵轴取向上为正方向;②两条数轴单位长度规定:一般情况下,横轴与纵轴单位长度相同,依据实际需要有时横轴与纵轴单位长度可以不同,但同一条数轴的单位长度必须相同.
【经典例题】
例题1、(1)已知点M到x轴的距离为6,到y轴距离为4,且在第四象限内,则点M的坐标为 .
(2)已知点Q在第二象限,它的横坐标与纵坐标之和为3,则点Q的坐标为______(写出一个即可)
【考点】点的坐标?
【分析】(1)根据点M(x, y)坐标的几何意义,可得=6,=4和第四象限内的点的坐标符号为(+,),即可得出答案.(2)由于Q点在第二象限,由此可以确定横坐标为负,纵坐标为正,又横坐标与纵坐标的和是3,由此可以确定Q点的坐标,答案不唯一.
【解答】(1)M到x轴的距离为6,到y轴距离为4,=6,=4且在第四象限内,∴点的坐标符号为(,+),∴点M的坐标为(4,6);
(2)∵Q点在第二象限,∴点的坐标符号为(,+),又横坐标与纵坐标的和是3,∴Q点的坐标为(1,4).
故答案为:(1, 4)(答案不唯一).
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(,+);第三象限(,);第四象限(+,).
例题2、已知:点A(5m+20,2m6).试分别根据下列条件,求出A点的坐标.
(1)点A在y轴上;
(2)点A在x轴上;
(3)点A的横坐标比纵坐标小1;
(4)点A的横坐标与纵坐标的比大为3︰4.
【考点】点的坐标.
【分析】(1)让横坐标为0求得m的值,代入点A的坐标即可求解;
(2)让纵坐标为0求得m的值,代入点A的坐标即可求解;
(3)让横坐标=纵坐标1得m的值,代入点A的坐标即可求解;
(4)让横坐标:纵坐标为=3:4,求得m的值,代入点A的坐标即可求解;
【解答】(1)令5m+20=0,解得m=4,所以A点的坐标为(0,14);
(2)令2m6=0,解得m=3,所以A点的坐标为(35,0);
(3)令5m+20=(2m6)1,解得m=3,所以A点的坐标为(5,12);
(4)根据题意,得,解得m=7.所以A点的坐标为(15,20).
【点评】此题考查了平面直角坐标系点坐标的符号特征,用到的知识点为列方程解决问题.
【夯实基础】
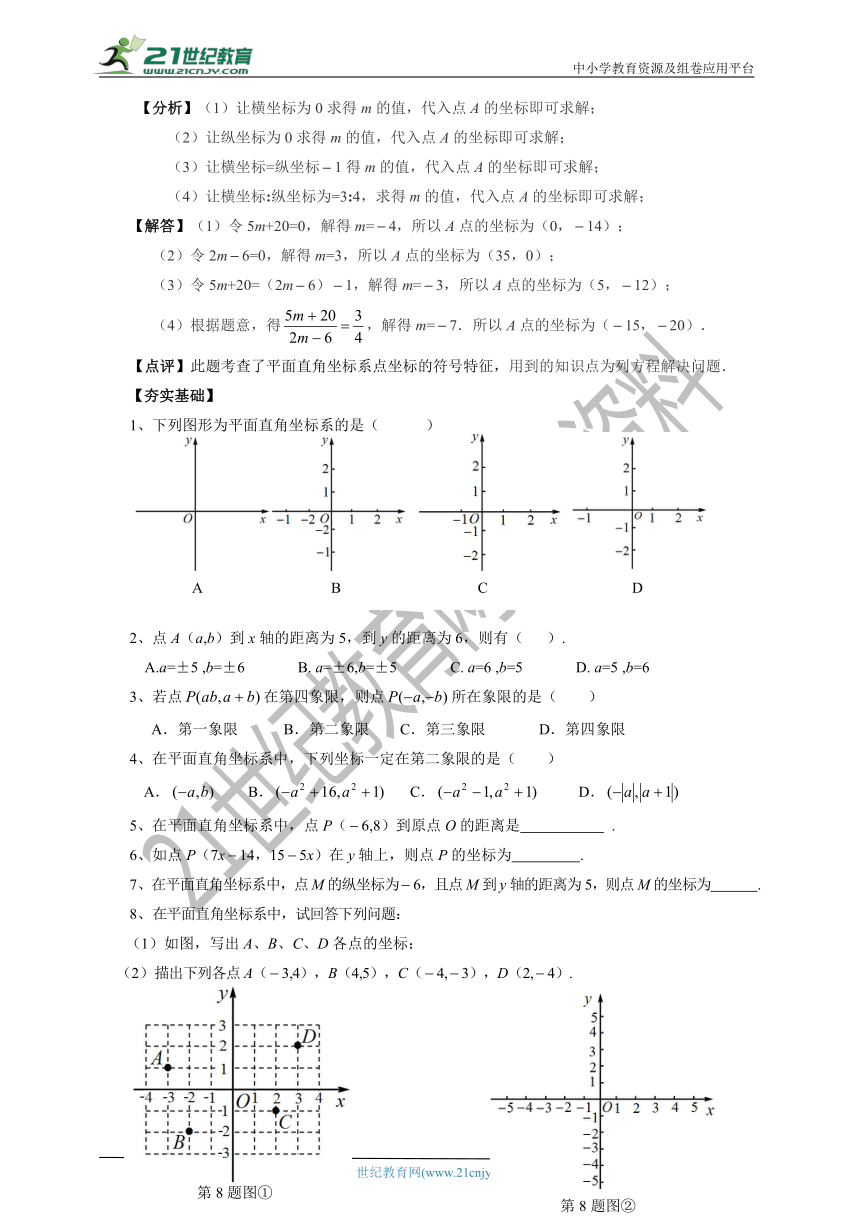
1、下列图形为平面直角坐标系的是( )
2、点A(a,b)到x轴的距离为5,到y的距离为6,则有( ).
A.a=±5 ,b=±6 B. a=±6,b=±5 C. a=6 ,b=5 D. a=5 ,b=6
3、若点在第四象限,则点所在象限的是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4、在平面直角坐标系中,下列坐标一定在第二象限的是( )
A. B. C. D.
5、在平面直角坐标系中,点P(6,8)到原点O的距离是 .
6、如点P(7x14,155x)在y轴上,则点P的坐标为 .
7、在平面直角坐标系中,点M的纵坐标为6,且点M到y轴的距离为5,则点M的坐标为 .
8、在平面直角坐标系中,试回答下列问题:
(1)如图,写出A、B、C、D各点的坐标;
(2)描出下列各点A(3,4),B(4,5),C(4,3),D(2,4).
【提优特训】
9、点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10、如图,在平面直角坐标系中,黑色部分盖住的点的坐标可能是( )
A. B. C. D.
11、若点A(2x3,3y+6)与点B(52x,2y)是同一个点,则P(x,y)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12、若点P(a,b)满足ab=0,那么点P在( )
A.原点 B.在横轴上 C.在纵轴上 D.在坐标轴上
13、在平面直角坐标系中,点,,,,根据你发现的规律写出点的坐标为 .
14、如图,某船在港口O沿着南偏东30°的方向,航行6海里到达A地,则点A的坐标为 .
15、已知点P(205a,2a12)在第三象限,且a取整数,则点P的坐标为 .
16、如图,写出△ABC各顶点的坐标,并求出△ABC的面积.
17、如图,在平面直角坐标系中,已知点A(3,0),B(3,0).
(1)画出所有的等腰直角三角形ABC;
(2)写出画出的等腰直角三角形ABC的顶点C的坐标.;
(3)分别求出以AB斜边和以AB的直角边的两个三角形的面积.
18、如图,如图,在平面直角坐标系中,
(1)写出A、B、C、D的坐标;
(2)试求四边形ABCD的面积.
【中考链接】
19、2018山东东营,在平面直角坐标系中,若点P(m2,m+1)在第二象限,则m的取值范围是( )
A.m<1 B.m>2 C.11
20、2018江苏扬州在平面直角坐标系的第二象限内有一点,点到轴的距离为3,到轴的距离为4,则点的坐标是( )
A. B. C. D.
21、2018浙江临安16.(3分)P(3,﹣4)到x轴的距离是 .
22、2018四川资阳如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,OA1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2018的坐标是 .
参考答案
1、C 2、B 3、A 4、C 5、10 6、(0,5) 7、(5, 6)(5, 6) 9、C 10、B
11、D 12、D 13、 14、 15、(5, 2) 19、C 20、C
21、4 22、
8、解:(1)A(3,1),B(2,2),C(2,1),D(3,2)
(2)如第8题图③
16、解:△ABC各顶点的坐标分别为A(2,1),
B(1,2),C(4,1)
17、解:(1)画出所有的等腰直角三角形ABC,如第17题图②;
(2),,,
,,.
(3)以AB为斜边:;
以AB为直角边:.
18、解:(1)A(1,2),B(8,3),C(9,6),D(5,8);
(2)
.
19、【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组求解即可.
【解答】解:∵点P(m2,m+1)在第二象限,
∴,
解得﹣1<m<2.
故选:C.
【点评】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
21、【分析】根据点在坐标系中坐标的几何意义即可解答.
【解答】解:根据点在坐标系中坐标的几何意义可知,P(3,4)到x轴的距离是|4|=4.
故答案为:4.
【点评】本题考查的是点的坐标的几何意义,横坐标的绝对值就是点到y轴的距离,纵坐标的绝对值就是点到x轴的距离.
22、【分析】本题点A坐标变化规律要分别从旋转
次数与点A所在象限或坐标轴、点A到原点
的距离与旋转次数的对应关系.
【解答】解:由已知,点A每次旋转转动45°,
则转动一周需转动8次,每次转动点A到原点
的距离变为转动前的倍
∵2018=252×8+2
∴点A2018的在y轴正半轴上,OA2018=
故答案为:(0,)
【点评】本题是平面直角坐标系下的规律探究题,除了研究动点变化的相关数据规律,还应该注意象限符号.
第1课时 平面直角坐标系(1)
【知识清单】
一、平面直角坐标系的含义及有关概念:
1. 平面直角坐标系有关概念:如图1,在平面内画两条互相垂直且有公共原点O的数轴,其中一条(通常画成水平的)叫做x轴或横轴,向右的方向为正方向;另一条(画成与x轴垂直的)叫做y轴或纵轴,向上的方向为正方向.这样就在平面内建立了平面直角坐标系,简称坐标系.坐标系所在的平面就叫做坐标平面,两坐标轴的公共原点O叫做直角坐标系的原点.?
2.点的坐标确定方法:如图2,对于平面内任意一点M,过M作MM1⊥x轴、MM2⊥y轴,设垂足M1,M2在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序实数对(x,y)叫做M点的坐标.??规定点的坐标用(x,y)表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒.
3.在直角坐标系中如何根据点的坐标找出这个点:如图3,如点P的坐标为(a,b),?在x轴上找到坐标为a的点A,过A作x轴的垂线,再在y轴上找到坐标为b的点B,过B作y轴的垂线,两垂线的交点即为所找的P点.??[来源:学科网ZXXK]
二、平面直角坐标系的象限的划分及象限中点的坐标符号的确定:如图4.?
? 1.象限划分:x轴和y轴把坐标平面分成四个象限,规定两条数轴的正方向的所夹的象限叫做第一象限,其它三个象限按逆时针方向依次叫做第二象限;第三象限;第四象限.坐标轴上的点不属于任何象限;
2.象限中点的坐标的符号的确定:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)?.若点P(x, y)在第一象限?x>0,y>0;点P(x, y)在第二象限?x<0,y>0;
点P(x, y)在第三象限?x<0,y<0;点P(x, y)在第四象限?x>0,y<0.
3.x轴,y轴上点的坐标的特征:点P(x, y)在x轴上?y为0(点纵坐标为0),x为任意实数,一般表示为P(x,0);点P(x,y)在y轴上?x为0(点横坐标为0),y为任意实数,一般表示为P(0,y).
三、点P(x, y)坐标的几何意义:
1.点P(x, y)到x轴的距离是;2.点P(x, y)到y袖的距离是;3. 点P(x, y)到原点的距离等于.
四、坐标与有序实数对的关系:
在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与之对应;反过来,对于任意一个有序实数对,在平面内都有的一点与它对应.
五、注意:
1. 有序实数对意义:(1)a与b要用逗号分开,以示它们是两个独立有序的数,又要用括号“包装”起来,表示它们是一个整体;(2)若a≠b则(a,b)与(b,a)表示两个不同的有序数对;(3)在直角坐标系中,有序数对(a,b)表示点的坐标,a,b依次表示横坐标、纵坐标.切记横坐标在前,坐标标在后.
2.组成平面直角坐标系的四个要素:①在同一平面内;②两条数轴;③互相垂直;④有公共原点.
3.两个规定:①正方向的规定:横轴取向右为正方向,纵轴取向上为正方向;②两条数轴单位长度规定:一般情况下,横轴与纵轴单位长度相同,依据实际需要有时横轴与纵轴单位长度可以不同,但同一条数轴的单位长度必须相同.
【经典例题】
例题1、(1)已知点M到x轴的距离为6,到y轴距离为4,且在第四象限内,则点M的坐标为 .
(2)已知点Q在第二象限,它的横坐标与纵坐标之和为3,则点Q的坐标为______(写出一个即可)
【考点】点的坐标?
【分析】(1)根据点M(x, y)坐标的几何意义,可得=6,=4和第四象限内的点的坐标符号为(+,),即可得出答案.(2)由于Q点在第二象限,由此可以确定横坐标为负,纵坐标为正,又横坐标与纵坐标的和是3,由此可以确定Q点的坐标,答案不唯一.
【解答】(1)M到x轴的距离为6,到y轴距离为4,=6,=4且在第四象限内,∴点的坐标符号为(,+),∴点M的坐标为(4,6);
(2)∵Q点在第二象限,∴点的坐标符号为(,+),又横坐标与纵坐标的和是3,∴Q点的坐标为(1,4).
故答案为:(1, 4)(答案不唯一).
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(,+);第三象限(,);第四象限(+,).
例题2、已知:点A(5m+20,2m6).试分别根据下列条件,求出A点的坐标.
(1)点A在y轴上;
(2)点A在x轴上;
(3)点A的横坐标比纵坐标小1;
(4)点A的横坐标与纵坐标的比大为3︰4.
【考点】点的坐标.
【分析】(1)让横坐标为0求得m的值,代入点A的坐标即可求解;
(2)让纵坐标为0求得m的值,代入点A的坐标即可求解;
(3)让横坐标=纵坐标1得m的值,代入点A的坐标即可求解;
(4)让横坐标:纵坐标为=3:4,求得m的值,代入点A的坐标即可求解;
【解答】(1)令5m+20=0,解得m=4,所以A点的坐标为(0,14);
(2)令2m6=0,解得m=3,所以A点的坐标为(35,0);
(3)令5m+20=(2m6)1,解得m=3,所以A点的坐标为(5,12);
(4)根据题意,得,解得m=7.所以A点的坐标为(15,20).
【点评】此题考查了平面直角坐标系点坐标的符号特征,用到的知识点为列方程解决问题.
【夯实基础】
1、下列图形为平面直角坐标系的是( )
2、点A(a,b)到x轴的距离为5,到y的距离为6,则有( ).
A.a=±5 ,b=±6 B. a=±6,b=±5 C. a=6 ,b=5 D. a=5 ,b=6
3、若点在第四象限,则点所在象限的是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4、在平面直角坐标系中,下列坐标一定在第二象限的是( )
A. B. C. D.
5、在平面直角坐标系中,点P(6,8)到原点O的距离是 .
6、如点P(7x14,155x)在y轴上,则点P的坐标为 .
7、在平面直角坐标系中,点M的纵坐标为6,且点M到y轴的距离为5,则点M的坐标为 .
8、在平面直角坐标系中,试回答下列问题:
(1)如图,写出A、B、C、D各点的坐标;
(2)描出下列各点A(3,4),B(4,5),C(4,3),D(2,4).
【提优特训】
9、点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10、如图,在平面直角坐标系中,黑色部分盖住的点的坐标可能是( )
A. B. C. D.
11、若点A(2x3,3y+6)与点B(52x,2y)是同一个点,则P(x,y)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12、若点P(a,b)满足ab=0,那么点P在( )
A.原点 B.在横轴上 C.在纵轴上 D.在坐标轴上
13、在平面直角坐标系中,点,,,,根据你发现的规律写出点的坐标为 .
14、如图,某船在港口O沿着南偏东30°的方向,航行6海里到达A地,则点A的坐标为 .
15、已知点P(205a,2a12)在第三象限,且a取整数,则点P的坐标为 .
16、如图,写出△ABC各顶点的坐标,并求出△ABC的面积.
17、如图,在平面直角坐标系中,已知点A(3,0),B(3,0).
(1)画出所有的等腰直角三角形ABC;
(2)写出画出的等腰直角三角形ABC的顶点C的坐标.;
(3)分别求出以AB斜边和以AB的直角边的两个三角形的面积.
18、如图,如图,在平面直角坐标系中,
(1)写出A、B、C、D的坐标;
(2)试求四边形ABCD的面积.
【中考链接】
19、2018山东东营,在平面直角坐标系中,若点P(m2,m+1)在第二象限,则m的取值范围是( )
A.m<1 B.m>2 C.1
20、2018江苏扬州在平面直角坐标系的第二象限内有一点,点到轴的距离为3,到轴的距离为4,则点的坐标是( )
A. B. C. D.
21、2018浙江临安16.(3分)P(3,﹣4)到x轴的距离是 .
22、2018四川资阳如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,OA1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2018的坐标是 .
参考答案
1、C 2、B 3、A 4、C 5、10 6、(0,5) 7、(5, 6)(5, 6) 9、C 10、B
11、D 12、D 13、 14、 15、(5, 2) 19、C 20、C
21、4 22、
8、解:(1)A(3,1),B(2,2),C(2,1),D(3,2)
(2)如第8题图③
16、解:△ABC各顶点的坐标分别为A(2,1),
B(1,2),C(4,1)
17、解:(1)画出所有的等腰直角三角形ABC,如第17题图②;
(2),,,
,,.
(3)以AB为斜边:;
以AB为直角边:.
18、解:(1)A(1,2),B(8,3),C(9,6),D(5,8);
(2)
.
19、【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组求解即可.
【解答】解:∵点P(m2,m+1)在第二象限,
∴,
解得﹣1<m<2.
故选:C.
【点评】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
21、【分析】根据点在坐标系中坐标的几何意义即可解答.
【解答】解:根据点在坐标系中坐标的几何意义可知,P(3,4)到x轴的距离是|4|=4.
故答案为:4.
【点评】本题考查的是点的坐标的几何意义,横坐标的绝对值就是点到y轴的距离,纵坐标的绝对值就是点到x轴的距离.
22、【分析】本题点A坐标变化规律要分别从旋转
次数与点A所在象限或坐标轴、点A到原点
的距离与旋转次数的对应关系.
【解答】解:由已知,点A每次旋转转动45°,
则转动一周需转动8次,每次转动点A到原点
的距离变为转动前的倍
∵2018=252×8+2
∴点A2018的在y轴正半轴上,OA2018=
故答案为:(0,)
【点评】本题是平面直角坐标系下的规律探究题,除了研究动点变化的相关数据规律,还应该注意象限符号.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
