4.2 平面直角坐标系(2)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 4.2 平面直角坐标系(2)(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 444.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-29 21:03:12 | ||
图片预览


文档简介
浙江版八年级数学上册第4章图形与坐标4.2平面直角坐标系
第2课时 平面直角坐标系(2)
【知识清单】
一、根据已知条件建立适当的直角坐标系解决实际问题:?
根据已知条件建立坐标系的要求是尽量使计算方便,一般地没有严格的规定,但有以下几条常用的方法:?
1.以某已知点为原点,使它坐标为(0,0);
2.以图形中某线段所在直线为x轴(或y轴);
3.以已知线段中点为原点;
4.以两直线交点为原点;
5.利用图形的轴对称性以对称轴为y轴等.
二、平行(或垂直)于坐标轴的直线上的点有如下特征:
1.平行于x轴(或垂直于y轴)的直线上的各点的纵坐标相等(等于这条直线与y轴的交点在y轴上的坐标), 横坐标不相等;若
2.平行于y轴(或垂直于x轴)的直线上的各点的横坐标相等(等于这条直线与x轴的交点在x轴上的坐标), 纵坐标不相等.
三、两坐标轴夹角平分线上的点的坐标特征
1.第一、三象限两坐标轴夹角平分线上的点的横坐标与纵坐标相等,一般记为(a,a)
2.第二、四象限两坐标轴夹角平分线上的点的横坐标与纵坐标相反,一般记为(a,a)
【经典例题】
例题1、如图所示,已知等边△ABC的边长为8,建立如下直角坐标系,解决问题.
(1)如图①,以等边△ABC的边AB所在的直线为x轴,边AB的垂直平分线为y轴,求顶点A、B、C的坐标;
(2)如图②,顶点A在原点上,求顶点A、B、C的坐标(直接写出即可);
(3)如图③,等边△ABC的两个顶点的坐标为A(5,0),B(3,0),求①顶点C的坐标(直接写出即可);②△ABC的面积.
【考点】:等边三角形的判定与性质;坐标与图形性质;三角形的面积;勾股定理.
?【分析】(1)因为AB=BC=CA=8,y轴所在的直线垂直平分AB,OA=OB=4,在RtAOC中,利用勾股定理可得,便可得到顶点A、B、C的坐标;
(2)作CD⊥AB于D,根据等腰三角形的三线合一的性质,因为点A在原点,AB=8,可得AD=BD=4,再根据勾股定理求得,便可得到顶点A、B、C的坐标;
(3)①作CE⊥AB于E.根据点A和B的坐标,得AB=8.根据等腰三角形的三线合一的性质,得AE=BE=4,又因为OB=3,所以OE=1,则点E的坐标为(1,0),再根据勾股定理求得,从而写出点C的坐标;②根据三角形的面积公式进行计算.
【解答】(1)如图①∵AB=BC=CA=8,y轴所在的直线是AB的垂直平分线,
∴OA=OB=4,
∴点A、B的坐标分别为(4,0)和(4,0)
在Rt△AOC中,CA=8,OA=4,
由勾股定理可得,
∴点C的坐标为.
∴顶点A、B、C的坐标分别为(4,0)、(4,0)、.
(2)如图②作CD⊥AB于D.
∴顶点A、B、C的坐标分别为(0,0)、(8,0)、.
(3)如图③,①作CE⊥AB于E.∴C点的坐标为;
②
【点评】1、此题综合运用了等边三角形的性质和勾股定理,熟练运用三角形的面积公式.x轴或(y轴)上两点间的距离等于两点的横坐标(纵坐标)的差的绝对值.
2、根据方便、简洁的原则建立平面直角坐标系. ①尽可能多的点(或边)落在坐标轴上;②方便表示各顶点的坐标;③借助图形的对称性.
例题2、在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.
【考点】等腰三角形的判定 、坐标与图形性质、勾股定理.
【分析】分别以O、A为圆心,以OA长为半径画弧,
与x坐标轴交点即为所求点P1、P2、P3,再作线段OA的
垂直平分线,与坐标轴的交点也是所求的点P4,作出图
形,利用数形结合
求解即可.
【解答】∵A(3,4),
∴,
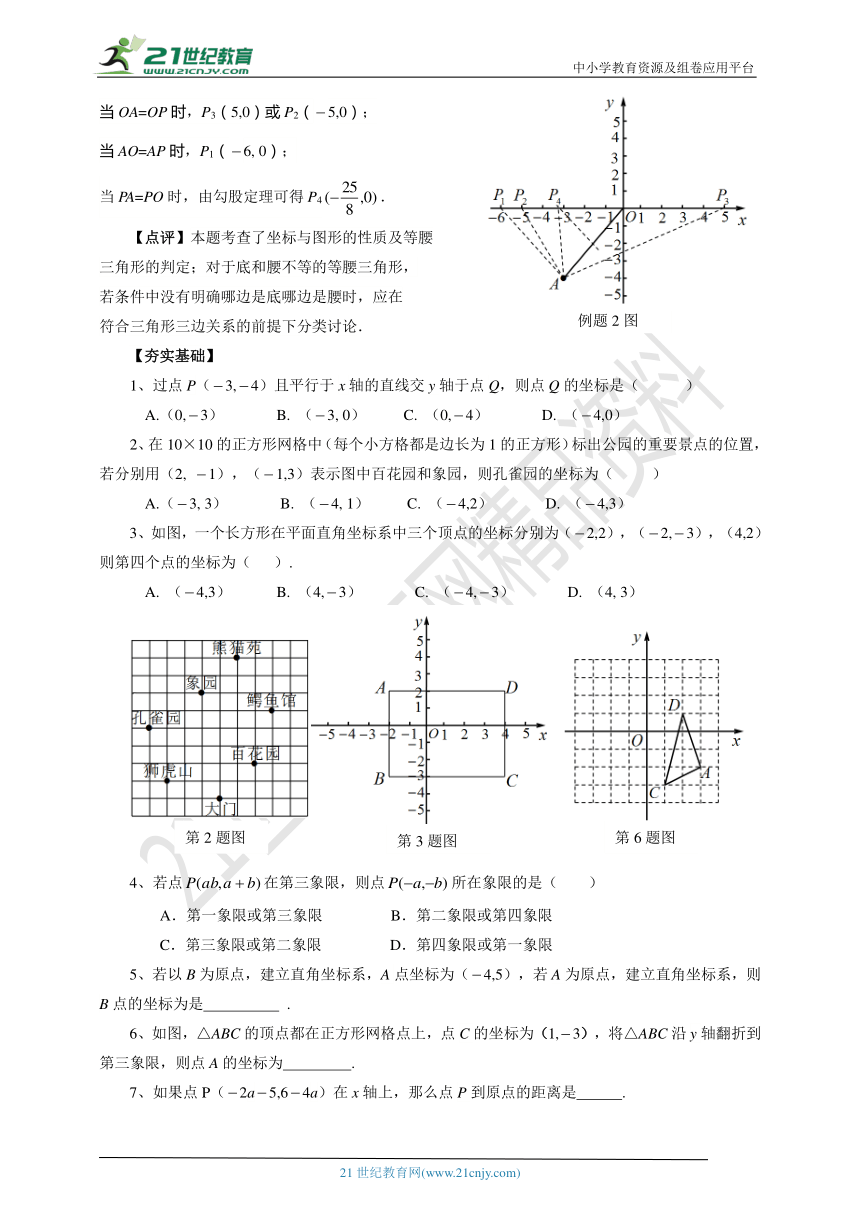
当OA=OP时,P3(5,0)或P2(5,0);
当AO=AP时,P1(6, 0);
当PA=PO时,由勾股定理可得P4.
【点评】本题考查了坐标与图形的性质及等腰
三角形的判定;对于底和腰不等的等腰三角形,
若条件中没有明确哪边是底哪边是腰时,应在
符合三角形三边关系的前提下分类讨论.
【夯实基础】
1、过点P(3,4)且平行于x轴的直线交y轴于点Q,则点Q的坐标是( )
A.(0,3) B. (3, 0) C. (0,4) D. (4,0)
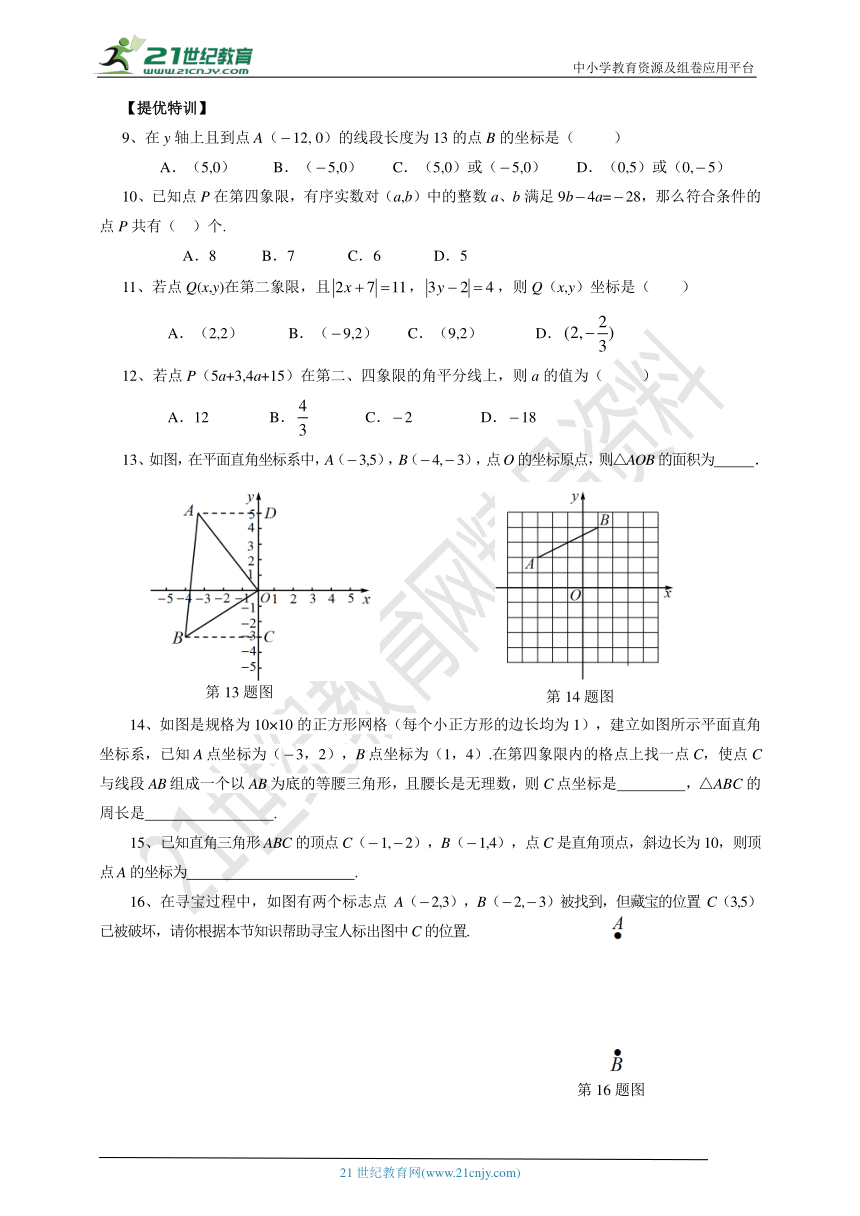
2、在10×10的正方形网格中(每个小方格都是边长为1的正方形)标出公园的重要景点的位置,若分别用(2, 1),(1,3)表示图中百花园和象园,则孔雀园的坐标为( )
A.(3, 3) B. (4, 1) C. (4,2) D. (4,3)
3、如图,一个长方形在平面直角坐标系中三个顶点的坐标分别为(2,2),(2,3),(4,2)则第四个点的坐标为( ).
A. (4,3) B. (4,3) C. (4,3) D. (4, 3)
4、若点在第三象限,则点所在象限的是( )
A.第一象限或第三象限 B.第二象限或第四象限
C.第三象限或第二象限 D.第四象限或第一象限
5、若以B为原点,建立直角坐标系,A点坐标为(4,5),若A为原点,建立直角坐标系,则B点的坐标为是 .
6、如图,△ABC的顶点都在正方形网格点上,点C的坐标为(1,3),将△ABC沿y轴翻折到第三象限,则点A的坐标为 .
7、如果点P(2a5,64a)在x轴上,那么点P到原点的距离是 .
【提优特训】
9、在y轴上且到点A(12, 0)的线段长度为13的点B的坐标是( )
A.(5,0) B.(5,0) C.(5,0)或(5,0) D.(0,5)或(0,5)
10、已知点P在第四象限,有序实数对(a,b)中的整数a、b满足9b4a=28,那么符合条件的点P共有( )个.
A.8 B.7 C.6 D.5
11、若点Q(x,y)在第二象限,且,,则Q(x,y)坐标是( )
A.(2,2) B.(9,2) C.(9,2) D.
12、若点P(5a+3,4a+15)在第二、四象限的角平分线上,则a的值为( )
A.12 B. C.2 D.18
13、如图,在平面直角坐标系中,A(3,5),B(4,3),点O的坐标原点,则△AOB的面积为 .
14、如图是规格为10×10的正方形网格(每个小正方形的边长均为1),建立如图所示平面直角坐标系,已知A点坐标为(3,2),B点坐标为(1,4).在第四象限内的格点上找一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ,△ABC的周长是 .
15、已知直角三角形ABC的顶点C(1,2),B(1,4),点C是直角顶点,斜边长为10,则顶点A的坐标为 .
16、在寻宝过程中,如图有两个标志点A(2,3),B(2,3)被找到,但藏宝的位置C(3,5)已被破坏,请你根据本节知识帮助寻宝人标出图中C的位置.
17、已知点A(1,0),B(5,0),C(x,y).
(1)若点C在第三象限且,,求点C的坐标及△ABC的面积;
(2)若点C在第二、四象限的角平分线上,且的面积为9,求点C的坐标.
18、先阅读理解下面的问题,再按要求解答问题:
如图,在平面直角坐标系中,已知两点,,如何求P1P2的距离.
若,,过P1,P2分别向x轴,y轴作垂线.垂足分别为A1(x1,0),A2(x2,0),B1(0, y1),B2(0, y2),Q(x2, y1).
因为,,
所以Rt△P1P2 Q中,
,
所以.
因此,我们得到平面上两点,
之间的距离公式为.
根据上面得到的公式,解决下列问题:
(1)已知平面两点A(2,3),B(4,11),求AB的距离;
(2)若平面三点A(2,1),B(4,3),C(3,4),试判定△ABC的形状,说明理由.
19、如图,△ABC是直角三角形,∠ACB=90°,点A、B在x轴上,CD是斜边AB的上的高,已知AD=4,BD=3,且点D的坐标为(1,0),
(1)求出A、B、C的坐标;
(2)试求△ABC的面积.
【中考链接】
20、2018新疆建设兵团,点(1,2)所在的象限是第 象限.
21、2018重庆綦江如图,点A的坐标是(2,2),若点P在x轴上,且APO是等腰三角形,则点P的坐标不可能的是( )
A. B. C. D.
22、2018?十堰如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是( )
A.2 B.
C.5 D.
参考答案
1、C 2、B 3、D 4、B 5、(4,5) 6、(2, 3) 7、8 9、D 10、C
11、B 12、C 13、28 14、、 15、(9,2)或 (7,2)
20、二 21、B 22、B
8、下列图形中,正方形的边长为4,请你写出各图中的正方形的顶点坐标.
A(0,0) . A(-2,0) .
B(4,0) . B(2,0) .
C(4,4) . C(2,4) .
D(0,4) . D(-2,4) .
. A(0,0).
. .
. C(4,0) .
.
16、解:(1)连接AB,作线段AB的垂直平分线,
垂足为D,线段AB的垂直平分线作为x轴;
(2)将AD三等分作直角坐标系的单位长度,
由点D向右截取DO等于两个单位长度;
(3)过点O作x轴的垂线,作为y轴;
(4)建立如图所示是平面直角坐标系,标出点C(3,5).
17、解:(1)如第17题图①∵,,
∴,.
∵点C在第三象限,∴点C的坐标为(5, 4)
过点C作CD⊥x轴与点D,
∵点C的坐标为(5, 4),∴.
∵A(1,0),B(5,0),
∴AB=6.
∴
(2)如第17题图②∵点C在第二、四象限的角平分线上,
∴x=y.
∴点到坐标轴的距离相等.
过点C作CD⊥x轴与点D,
∵A(1,0),B(5,0),
∴AB=6.
∴
∴
解得, ∴.
∴点C的坐标为(3,3).
18、解:(1)∵A(2,3),B(2,7),
由两点间的距离公式,得
∴.
(2)∵A(2,1),B(4,3),C(3,4),
由两点间的距离公式,得
∴,
∴,
∴
∵,.
∴
∴△ABC是直角三角形.
19、解:(1)∵AD=4,BD=3,且点D的坐标为(1,0),
∴点A、B的坐标分别为(5,0),(2,0)
在RtADC中,
在RtBDC中,
①②得,,
在RtABC中,,
由③、④得,,
将代入①得.
∴点C的坐标为.
(2)由(1)知,AB=7,
第2课时 平面直角坐标系(2)
【知识清单】
一、根据已知条件建立适当的直角坐标系解决实际问题:?
根据已知条件建立坐标系的要求是尽量使计算方便,一般地没有严格的规定,但有以下几条常用的方法:?
1.以某已知点为原点,使它坐标为(0,0);
2.以图形中某线段所在直线为x轴(或y轴);
3.以已知线段中点为原点;
4.以两直线交点为原点;
5.利用图形的轴对称性以对称轴为y轴等.
二、平行(或垂直)于坐标轴的直线上的点有如下特征:
1.平行于x轴(或垂直于y轴)的直线上的各点的纵坐标相等(等于这条直线与y轴的交点在y轴上的坐标), 横坐标不相等;若
2.平行于y轴(或垂直于x轴)的直线上的各点的横坐标相等(等于这条直线与x轴的交点在x轴上的坐标), 纵坐标不相等.
三、两坐标轴夹角平分线上的点的坐标特征
1.第一、三象限两坐标轴夹角平分线上的点的横坐标与纵坐标相等,一般记为(a,a)
2.第二、四象限两坐标轴夹角平分线上的点的横坐标与纵坐标相反,一般记为(a,a)
【经典例题】
例题1、如图所示,已知等边△ABC的边长为8,建立如下直角坐标系,解决问题.
(1)如图①,以等边△ABC的边AB所在的直线为x轴,边AB的垂直平分线为y轴,求顶点A、B、C的坐标;
(2)如图②,顶点A在原点上,求顶点A、B、C的坐标(直接写出即可);
(3)如图③,等边△ABC的两个顶点的坐标为A(5,0),B(3,0),求①顶点C的坐标(直接写出即可);②△ABC的面积.
【考点】:等边三角形的判定与性质;坐标与图形性质;三角形的面积;勾股定理.
?【分析】(1)因为AB=BC=CA=8,y轴所在的直线垂直平分AB,OA=OB=4,在RtAOC中,利用勾股定理可得,便可得到顶点A、B、C的坐标;
(2)作CD⊥AB于D,根据等腰三角形的三线合一的性质,因为点A在原点,AB=8,可得AD=BD=4,再根据勾股定理求得,便可得到顶点A、B、C的坐标;
(3)①作CE⊥AB于E.根据点A和B的坐标,得AB=8.根据等腰三角形的三线合一的性质,得AE=BE=4,又因为OB=3,所以OE=1,则点E的坐标为(1,0),再根据勾股定理求得,从而写出点C的坐标;②根据三角形的面积公式进行计算.
【解答】(1)如图①∵AB=BC=CA=8,y轴所在的直线是AB的垂直平分线,
∴OA=OB=4,
∴点A、B的坐标分别为(4,0)和(4,0)
在Rt△AOC中,CA=8,OA=4,
由勾股定理可得,
∴点C的坐标为.
∴顶点A、B、C的坐标分别为(4,0)、(4,0)、.
(2)如图②作CD⊥AB于D.
∴顶点A、B、C的坐标分别为(0,0)、(8,0)、.
(3)如图③,①作CE⊥AB于E.∴C点的坐标为;
②
【点评】1、此题综合运用了等边三角形的性质和勾股定理,熟练运用三角形的面积公式.x轴或(y轴)上两点间的距离等于两点的横坐标(纵坐标)的差的绝对值.
2、根据方便、简洁的原则建立平面直角坐标系. ①尽可能多的点(或边)落在坐标轴上;②方便表示各顶点的坐标;③借助图形的对称性.
例题2、在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.
【考点】等腰三角形的判定 、坐标与图形性质、勾股定理.
【分析】分别以O、A为圆心,以OA长为半径画弧,
与x坐标轴交点即为所求点P1、P2、P3,再作线段OA的
垂直平分线,与坐标轴的交点也是所求的点P4,作出图
形,利用数形结合
求解即可.
【解答】∵A(3,4),
∴,
当OA=OP时,P3(5,0)或P2(5,0);
当AO=AP时,P1(6, 0);
当PA=PO时,由勾股定理可得P4.
【点评】本题考查了坐标与图形的性质及等腰
三角形的判定;对于底和腰不等的等腰三角形,
若条件中没有明确哪边是底哪边是腰时,应在
符合三角形三边关系的前提下分类讨论.
【夯实基础】
1、过点P(3,4)且平行于x轴的直线交y轴于点Q,则点Q的坐标是( )
A.(0,3) B. (3, 0) C. (0,4) D. (4,0)
2、在10×10的正方形网格中(每个小方格都是边长为1的正方形)标出公园的重要景点的位置,若分别用(2, 1),(1,3)表示图中百花园和象园,则孔雀园的坐标为( )
A.(3, 3) B. (4, 1) C. (4,2) D. (4,3)
3、如图,一个长方形在平面直角坐标系中三个顶点的坐标分别为(2,2),(2,3),(4,2)则第四个点的坐标为( ).
A. (4,3) B. (4,3) C. (4,3) D. (4, 3)
4、若点在第三象限,则点所在象限的是( )
A.第一象限或第三象限 B.第二象限或第四象限
C.第三象限或第二象限 D.第四象限或第一象限
5、若以B为原点,建立直角坐标系,A点坐标为(4,5),若A为原点,建立直角坐标系,则B点的坐标为是 .
6、如图,△ABC的顶点都在正方形网格点上,点C的坐标为(1,3),将△ABC沿y轴翻折到第三象限,则点A的坐标为 .
7、如果点P(2a5,64a)在x轴上,那么点P到原点的距离是 .
【提优特训】
9、在y轴上且到点A(12, 0)的线段长度为13的点B的坐标是( )
A.(5,0) B.(5,0) C.(5,0)或(5,0) D.(0,5)或(0,5)
10、已知点P在第四象限,有序实数对(a,b)中的整数a、b满足9b4a=28,那么符合条件的点P共有( )个.
A.8 B.7 C.6 D.5
11、若点Q(x,y)在第二象限,且,,则Q(x,y)坐标是( )
A.(2,2) B.(9,2) C.(9,2) D.
12、若点P(5a+3,4a+15)在第二、四象限的角平分线上,则a的值为( )
A.12 B. C.2 D.18
13、如图,在平面直角坐标系中,A(3,5),B(4,3),点O的坐标原点,则△AOB的面积为 .
14、如图是规格为10×10的正方形网格(每个小正方形的边长均为1),建立如图所示平面直角坐标系,已知A点坐标为(3,2),B点坐标为(1,4).在第四象限内的格点上找一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ,△ABC的周长是 .
15、已知直角三角形ABC的顶点C(1,2),B(1,4),点C是直角顶点,斜边长为10,则顶点A的坐标为 .
16、在寻宝过程中,如图有两个标志点A(2,3),B(2,3)被找到,但藏宝的位置C(3,5)已被破坏,请你根据本节知识帮助寻宝人标出图中C的位置.
17、已知点A(1,0),B(5,0),C(x,y).
(1)若点C在第三象限且,,求点C的坐标及△ABC的面积;
(2)若点C在第二、四象限的角平分线上,且的面积为9,求点C的坐标.
18、先阅读理解下面的问题,再按要求解答问题:
如图,在平面直角坐标系中,已知两点,,如何求P1P2的距离.
若,,过P1,P2分别向x轴,y轴作垂线.垂足分别为A1(x1,0),A2(x2,0),B1(0, y1),B2(0, y2),Q(x2, y1).
因为,,
所以Rt△P1P2 Q中,
,
所以.
因此,我们得到平面上两点,
之间的距离公式为.
根据上面得到的公式,解决下列问题:
(1)已知平面两点A(2,3),B(4,11),求AB的距离;
(2)若平面三点A(2,1),B(4,3),C(3,4),试判定△ABC的形状,说明理由.
19、如图,△ABC是直角三角形,∠ACB=90°,点A、B在x轴上,CD是斜边AB的上的高,已知AD=4,BD=3,且点D的坐标为(1,0),
(1)求出A、B、C的坐标;
(2)试求△ABC的面积.
【中考链接】
20、2018新疆建设兵团,点(1,2)所在的象限是第 象限.
21、2018重庆綦江如图,点A的坐标是(2,2),若点P在x轴上,且APO是等腰三角形,则点P的坐标不可能的是( )
A. B. C. D.
22、2018?十堰如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是( )
A.2 B.
C.5 D.
参考答案
1、C 2、B 3、D 4、B 5、(4,5) 6、(2, 3) 7、8 9、D 10、C
11、B 12、C 13、28 14、、 15、(9,2)或 (7,2)
20、二 21、B 22、B
8、下列图形中,正方形的边长为4,请你写出各图中的正方形的顶点坐标.
A(0,0) . A(-2,0) .
B(4,0) . B(2,0) .
C(4,4) . C(2,4) .
D(0,4) . D(-2,4) .
. A(0,0).
. .
. C(4,0) .
.
16、解:(1)连接AB,作线段AB的垂直平分线,
垂足为D,线段AB的垂直平分线作为x轴;
(2)将AD三等分作直角坐标系的单位长度,
由点D向右截取DO等于两个单位长度;
(3)过点O作x轴的垂线,作为y轴;
(4)建立如图所示是平面直角坐标系,标出点C(3,5).
17、解:(1)如第17题图①∵,,
∴,.
∵点C在第三象限,∴点C的坐标为(5, 4)
过点C作CD⊥x轴与点D,
∵点C的坐标为(5, 4),∴.
∵A(1,0),B(5,0),
∴AB=6.
∴
(2)如第17题图②∵点C在第二、四象限的角平分线上,
∴x=y.
∴点到坐标轴的距离相等.
过点C作CD⊥x轴与点D,
∵A(1,0),B(5,0),
∴AB=6.
∴
∴
解得, ∴.
∴点C的坐标为(3,3).
18、解:(1)∵A(2,3),B(2,7),
由两点间的距离公式,得
∴.
(2)∵A(2,1),B(4,3),C(3,4),
由两点间的距离公式,得
∴,
∴,
∴
∵,.
∴
∴△ABC是直角三角形.
19、解:(1)∵AD=4,BD=3,且点D的坐标为(1,0),
∴点A、B的坐标分别为(5,0),(2,0)
在RtADC中,
在RtBDC中,
①②得,,
在RtABC中,,
由③、④得,,
将代入①得.
∴点C的坐标为.
(2)由(1)知,AB=7,
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
