4.3 坐标平面内图形的轴对称和平移(1)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 4.3 坐标平面内图形的轴对称和平移(1)(知识清单+经典例题+夯实基础+提优训练+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 402.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 17:24:08 | ||
图片预览


文档简介
浙江版八年级数学上册第4章图形与坐标4.3坐标平面内图形的轴对称和平移
第1课时 坐标平面内图形的轴对称和平移(1)
【知识清单】
一、关于坐标轴、原点对称的点的坐标的特征:
1.在直角坐标系中,点(a,b)关于x轴对称的点的坐标为(a,b);即:横坐标保持不变,纵坐标分别乘以1,所得图形与原图形关于x轴对称.
2.在直角坐标系中,点(a,b)关于y轴对称的点的坐标为(a,b);即:纵坐标保持不变,横坐标分别乘以1,所得图形与原图形关于y轴对称.
3.在直角坐标系中,点(a,b)关于原点对称的点的坐标为(a,b);即:横、纵坐标分别乘以1,所得图形与原图形关于原点对称.
二、口诀:
1.横轴(x轴)对称,横坐标不变,纵坐标变相反;2. 纵轴(y轴)对称,纵坐标不变,横坐标变相反.
三:在直角坐标系中画对称图形:
1.使对称轴与坐标轴重合;2.画出一侧的关键点,并求出坐标;3.利用坐标系,求另一侧的关键点的坐标;4.描点、连线.
四、注意事项:
1.分清对称前后图形的顶点坐标的所在象限的特征;2. 描点要准确、连线用直尺.
【经典例题】
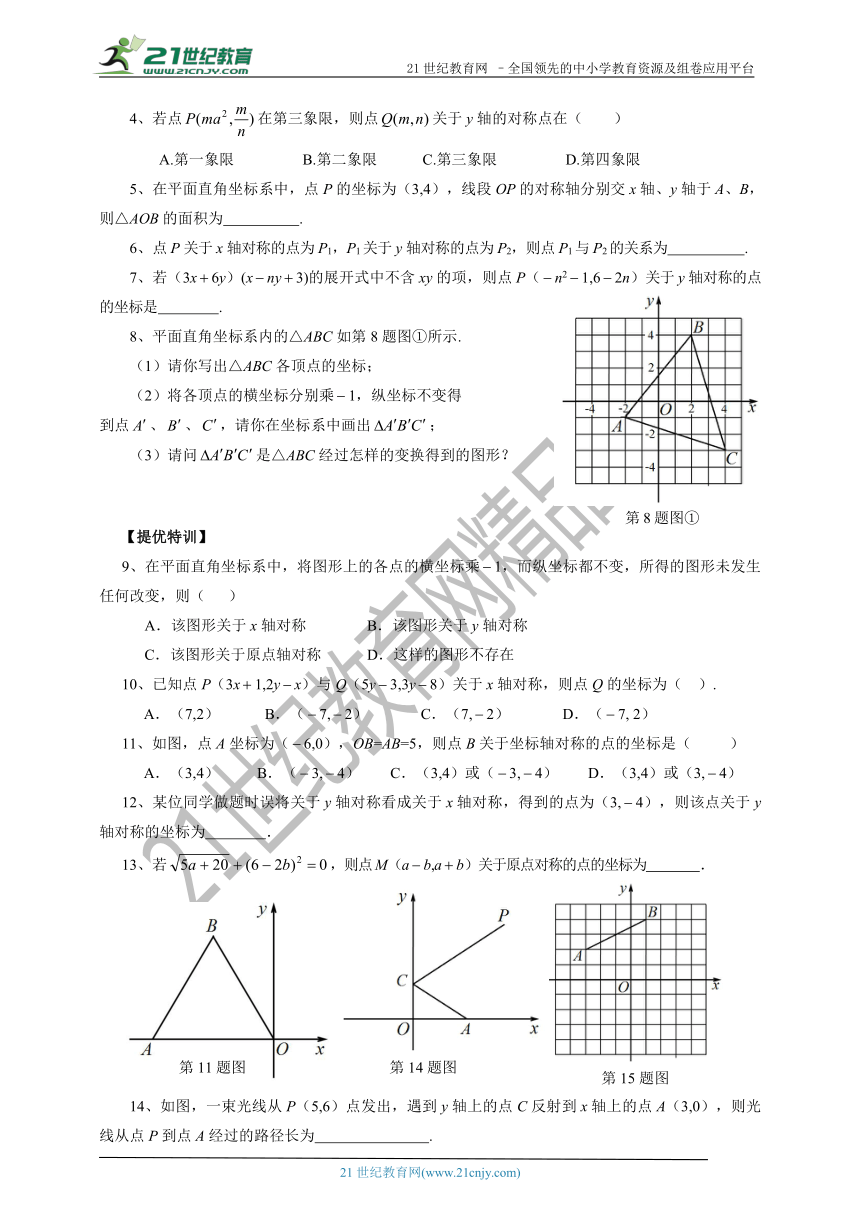
例题1、如图中“鱼”的顶点的横坐标不变,纵坐标分别乘以1,画出图形说明它与原图形的关系.?
【考点】:关于x轴、y轴对称的点的坐标.
【分析】横坐标不变,纵坐标分别乘以1,就是横坐标不变,纵坐标变成相反数,所得图形与原图形关于x轴对称.
【解答】解:原图形的坐标为(0,0)(5,4)、(3,0)、(4,3)、(6,2)、(6,0)、(6,2).
纵坐标乘以-1后各顶点坐标分别为(0,0)(5,4)、(3,0)、(4, 3)、(6,2)、(6,0)、
(6, 2).描点、连线如图(2)所示,所得图形与原图形关于x轴成对称.
【点评】本题主要考查了利用坐标判断两个图形关于坐标轴对称的方法,横坐标不变,纵坐标变成相反数则关于横轴的对称;纵坐标不变,横坐标变成相反数则关于纵轴的对称.
例题2、已知两点A(3,4),B(5,2),点P是x轴上的一点,求PA+PB的最小值.
【考点】点的对称、勾股定理.
【分析】?求两线段之和最小,通常的做法是将
两条线段拼一条线段.关于线段最短,我们有“两点之间,
线段最短”.因此有过点A作关于x轴的对称点A′,连结AB′,
交x轴于点P,点P就是要求的点.由对称性可知AP=A′P,
PAPB= PA′PB=A′B,然后再利用勾股定理求得AB的长即可.
【解答】如图②,(1)作出点A关于x轴的对称
点A′(3,4),D是垂足,
(2)连结AB′,交x轴于点P,点P就是要求的点.
(3)过B作BF⊥x轴,F是垂足,过A′作B′E⊥y轴,E是垂足,
(4)延长BF、A′E相交于点Q,则Q的坐标为(4,5).
由对称性可知AP=A′P,PAPB= PA′PB=A′B;
而A′、B两点间线段最短,
∴AB′最短,(两点之间,线段最短),即AP+PB最小,
∴在Rt△A′QB中,A′Q=8,QB=6,
∴
即PA+PB的最小值为10.
【点评】?此题主要考查了轴对称最短路线问题,
求两线段之和最小的基本方法是作其中一个已知
点关于直线的对称点,从而将两条线段之和转化为
另一个已知点与对称点之间的线段.
【夯实基础】
1、点P(5,7)关于y轴的对称点的坐标是( )
A.(5,7) B.(5, 7) C.(5,7) D.(5,7)
2、在等边三角形中,顶点B的坐标为,若顶点C与顶点B关于x轴对称,则顶点A坐标是( )
A.(3,0) B.(3, 0) C. D.(3,0)或(3,0)
3、已知P(mn,mn)在第四象限,则平面直角坐标系中四个点A(m,n),B(m,n),
C(m,n),D(m,n)中关于x轴对称的是( ).
A. A与C,B与D B. A与B,D与C C. A与D,A与C D. A与D,B与C
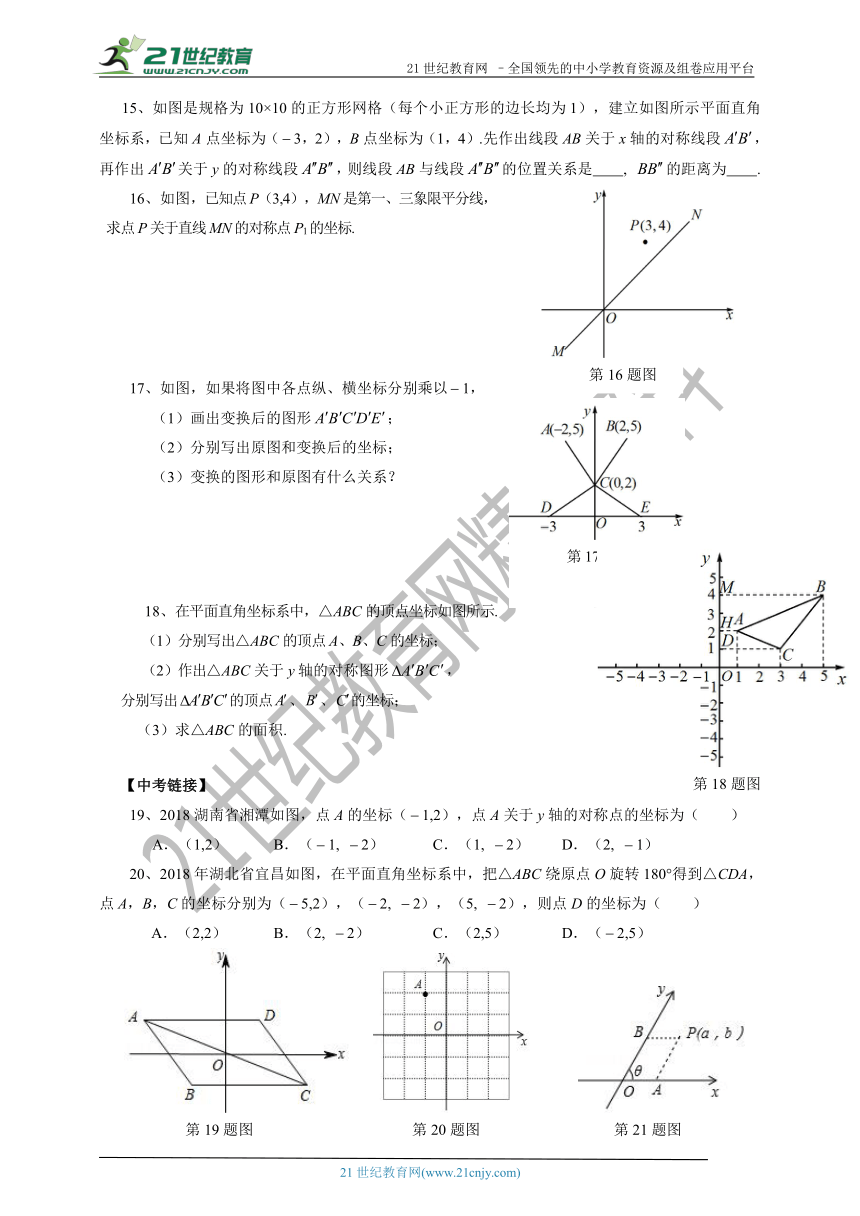
4、若点在第三象限,则点关于y轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5、在平面直角坐标系中,点P的坐标为(3,4),线段OP的对称轴分别交x轴、y轴于A、B,则△AOB的面积为 .
6、点P关于x轴对称的点为P1,P1关于y轴对称的点为P2,则点P1与P2的关系为 .
7、若(3x6y)(xny3)的展开式中不含xy的项,则点P(n21,62n)关于y轴对称的点的坐标是 .
8、平面直角坐标系内的△ABC如第8题图①所示.
(1)请你写出△ABC各顶点的坐标;
(2)将各顶点的横坐标分别乘1,纵坐标不变得
到点、、,请你在坐标系中画出;
(3)请问是△ABC经过怎样的变换得到的图形?
【提优特训】
9、在平面直角坐标系中,将图形上的各点的横坐标乘1,而纵坐标都不变,所得的图形未发生任何改变,则( )
A.该图形关于x轴对称 B.该图形关于y轴对称
C.该图形关于原点轴对称 D.这样的图形不存在
10、已知点P(3x1,2yx)与Q(5y3,3y8)关于x轴对称,则点Q的坐标为( ).
A.(7,2) B.(7,2) C.(7,2) D.(7, 2)
11、如图,点A坐标为(6,0),OB=AB=5,则点B关于坐标轴对称的点的坐标是( )
A.(3,4) B.(3,4) C.(3,4)或(3,4) D.(3,4)或(3,4)
12、某位同学做题时误将关于y轴对称看成关于x轴对称,得到的点为(3,4),则该点关于y轴对称的坐标为 .
13、若,则点M(ab,ab)关于原点对称的点的坐标为 .
14、如图,一束光线从P(5,6)点发出,遇到y轴上的点C反射到x轴上的点A(3,0),则光线从点P到点A经过的路径长为 .
15、如图是规格为10×10的正方形网格(每个小正方形的边长均为1),建立如图所示平面直角坐标系,已知A点坐标为(3,2),B点坐标为(1,4).先作出线段AB关于x轴的对称线段,再作出关于y的对称线段,则线段AB与线段的位置关系是 , 的距离为 .
16、如图,已知点P(3,4),MN是第一、三象限平分线,
求点P关于直线MN的对称点P1的坐标.
17、如图,如果将图中各点纵、横坐标分别乘以1,
(1)画出变换后的图形;
(2)分别写出原图和变换后的坐标;
(3)变换的图形和原图有什么关系?
18、在平面直角坐标系中,△ABC的顶点坐标如图所示.
(1)分别写出△ABC的顶点A、B、C的坐标;
(2)作出△ABC关于y轴的对称图形,
分别写出的顶点、、的坐标;
(3)求△ABC的面积.
【中考链接】
19、2018湖南省湘潭如图,点A的坐标(1,2),点A关于y轴的对称点的坐标为( )
A.(1,2) B.(1, 2) C.(1, 2) D.(2, 1)
20、2018年湖北省宜昌如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(5,2),(2, 2),(5, 2),则点D的坐标为( )
A.(2,2) B.(2, 2) C.(2,5) D.(2,5)
21、2018浙江台州如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
22、2018?黑龙江大庆在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .
参考答案
1、C 2、D 3、C 4、A 5、 6、关于原点对称 7、(5, 2) 9、B 10、B
11、C 12、(3, 4) 13、(7,1) 14、10 15、平行、
19、A 20、A 21、(2, 5) 22、12
8、解:(1)A(2,1),B(2,4),C(4,3);
(2)画图,如第8题图②,
(2,1),B(2,4),C(4,3);
(3)是△ABC关于y轴对称图形.
16 解:过点P作PE⊥MN于的E,延长PE带P1 ,使PE= P1E,
则点P1就是点P关于直线MN的对称点.
连接OP、OP1,则有OP=OP1,∠POE=∠P1OE.
过点P作PD⊥y轴于D,P1作P1H⊥x轴于H.
∵MN是第一、三象限平分线,
∴∠DOE=∠HOE=45°.
∠1=∠2.
在Rt△PDO和Rt△P1HO中,
∵
∴Rt△PDO≌Rt△P1HO(AAS),
∴PD=P1H=3,OD= OH=4,
∴P1的坐标为(4,3).
17、解:(1)如图;
(2)原图坐标 变换后图形坐标
A(2,5)
B(2,5)
C(0,2)
D(3,0)
E(3,0)
(3)变换的图形和原图的关系是关于原点对称(或关于x轴对称).
18、解:(1)根据图形可得△ABC的顶点坐标分别为:
A(1,2),B(5,4),C(3,1);
(2)作出△ABC关于y轴的对称图形如图所示;
根据对称的性质可得的顶点坐标分别为:
(1,2),(5,4),(3,1);
(3)△ABC的面积为
第1课时 坐标平面内图形的轴对称和平移(1)
【知识清单】
一、关于坐标轴、原点对称的点的坐标的特征:
1.在直角坐标系中,点(a,b)关于x轴对称的点的坐标为(a,b);即:横坐标保持不变,纵坐标分别乘以1,所得图形与原图形关于x轴对称.
2.在直角坐标系中,点(a,b)关于y轴对称的点的坐标为(a,b);即:纵坐标保持不变,横坐标分别乘以1,所得图形与原图形关于y轴对称.
3.在直角坐标系中,点(a,b)关于原点对称的点的坐标为(a,b);即:横、纵坐标分别乘以1,所得图形与原图形关于原点对称.
二、口诀:
1.横轴(x轴)对称,横坐标不变,纵坐标变相反;2. 纵轴(y轴)对称,纵坐标不变,横坐标变相反.
三:在直角坐标系中画对称图形:
1.使对称轴与坐标轴重合;2.画出一侧的关键点,并求出坐标;3.利用坐标系,求另一侧的关键点的坐标;4.描点、连线.
四、注意事项:
1.分清对称前后图形的顶点坐标的所在象限的特征;2. 描点要准确、连线用直尺.
【经典例题】
例题1、如图中“鱼”的顶点的横坐标不变,纵坐标分别乘以1,画出图形说明它与原图形的关系.?
【考点】:关于x轴、y轴对称的点的坐标.
【分析】横坐标不变,纵坐标分别乘以1,就是横坐标不变,纵坐标变成相反数,所得图形与原图形关于x轴对称.
【解答】解:原图形的坐标为(0,0)(5,4)、(3,0)、(4,3)、(6,2)、(6,0)、(6,2).
纵坐标乘以-1后各顶点坐标分别为(0,0)(5,4)、(3,0)、(4, 3)、(6,2)、(6,0)、
(6, 2).描点、连线如图(2)所示,所得图形与原图形关于x轴成对称.
【点评】本题主要考查了利用坐标判断两个图形关于坐标轴对称的方法,横坐标不变,纵坐标变成相反数则关于横轴的对称;纵坐标不变,横坐标变成相反数则关于纵轴的对称.
例题2、已知两点A(3,4),B(5,2),点P是x轴上的一点,求PA+PB的最小值.
【考点】点的对称、勾股定理.
【分析】?求两线段之和最小,通常的做法是将
两条线段拼一条线段.关于线段最短,我们有“两点之间,
线段最短”.因此有过点A作关于x轴的对称点A′,连结AB′,
交x轴于点P,点P就是要求的点.由对称性可知AP=A′P,
PAPB= PA′PB=A′B,然后再利用勾股定理求得AB的长即可.
【解答】如图②,(1)作出点A关于x轴的对称
点A′(3,4),D是垂足,
(2)连结AB′,交x轴于点P,点P就是要求的点.
(3)过B作BF⊥x轴,F是垂足,过A′作B′E⊥y轴,E是垂足,
(4)延长BF、A′E相交于点Q,则Q的坐标为(4,5).
由对称性可知AP=A′P,PAPB= PA′PB=A′B;
而A′、B两点间线段最短,
∴AB′最短,(两点之间,线段最短),即AP+PB最小,
∴在Rt△A′QB中,A′Q=8,QB=6,
∴
即PA+PB的最小值为10.
【点评】?此题主要考查了轴对称最短路线问题,
求两线段之和最小的基本方法是作其中一个已知
点关于直线的对称点,从而将两条线段之和转化为
另一个已知点与对称点之间的线段.
【夯实基础】
1、点P(5,7)关于y轴的对称点的坐标是( )
A.(5,7) B.(5, 7) C.(5,7) D.(5,7)
2、在等边三角形中,顶点B的坐标为,若顶点C与顶点B关于x轴对称,则顶点A坐标是( )
A.(3,0) B.(3, 0) C. D.(3,0)或(3,0)
3、已知P(mn,mn)在第四象限,则平面直角坐标系中四个点A(m,n),B(m,n),
C(m,n),D(m,n)中关于x轴对称的是( ).
A. A与C,B与D B. A与B,D与C C. A与D,A与C D. A与D,B与C
4、若点在第三象限,则点关于y轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5、在平面直角坐标系中,点P的坐标为(3,4),线段OP的对称轴分别交x轴、y轴于A、B,则△AOB的面积为 .
6、点P关于x轴对称的点为P1,P1关于y轴对称的点为P2,则点P1与P2的关系为 .
7、若(3x6y)(xny3)的展开式中不含xy的项,则点P(n21,62n)关于y轴对称的点的坐标是 .
8、平面直角坐标系内的△ABC如第8题图①所示.
(1)请你写出△ABC各顶点的坐标;
(2)将各顶点的横坐标分别乘1,纵坐标不变得
到点、、,请你在坐标系中画出;
(3)请问是△ABC经过怎样的变换得到的图形?
【提优特训】
9、在平面直角坐标系中,将图形上的各点的横坐标乘1,而纵坐标都不变,所得的图形未发生任何改变,则( )
A.该图形关于x轴对称 B.该图形关于y轴对称
C.该图形关于原点轴对称 D.这样的图形不存在
10、已知点P(3x1,2yx)与Q(5y3,3y8)关于x轴对称,则点Q的坐标为( ).
A.(7,2) B.(7,2) C.(7,2) D.(7, 2)
11、如图,点A坐标为(6,0),OB=AB=5,则点B关于坐标轴对称的点的坐标是( )
A.(3,4) B.(3,4) C.(3,4)或(3,4) D.(3,4)或(3,4)
12、某位同学做题时误将关于y轴对称看成关于x轴对称,得到的点为(3,4),则该点关于y轴对称的坐标为 .
13、若,则点M(ab,ab)关于原点对称的点的坐标为 .
14、如图,一束光线从P(5,6)点发出,遇到y轴上的点C反射到x轴上的点A(3,0),则光线从点P到点A经过的路径长为 .
15、如图是规格为10×10的正方形网格(每个小正方形的边长均为1),建立如图所示平面直角坐标系,已知A点坐标为(3,2),B点坐标为(1,4).先作出线段AB关于x轴的对称线段,再作出关于y的对称线段,则线段AB与线段的位置关系是 , 的距离为 .
16、如图,已知点P(3,4),MN是第一、三象限平分线,
求点P关于直线MN的对称点P1的坐标.
17、如图,如果将图中各点纵、横坐标分别乘以1,
(1)画出变换后的图形;
(2)分别写出原图和变换后的坐标;
(3)变换的图形和原图有什么关系?
18、在平面直角坐标系中,△ABC的顶点坐标如图所示.
(1)分别写出△ABC的顶点A、B、C的坐标;
(2)作出△ABC关于y轴的对称图形,
分别写出的顶点、、的坐标;
(3)求△ABC的面积.
【中考链接】
19、2018湖南省湘潭如图,点A的坐标(1,2),点A关于y轴的对称点的坐标为( )
A.(1,2) B.(1, 2) C.(1, 2) D.(2, 1)
20、2018年湖北省宜昌如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(5,2),(2, 2),(5, 2),则点D的坐标为( )
A.(2,2) B.(2, 2) C.(2,5) D.(2,5)
21、2018浙江台州如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
22、2018?黑龙江大庆在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .
参考答案
1、C 2、D 3、C 4、A 5、 6、关于原点对称 7、(5, 2) 9、B 10、B
11、C 12、(3, 4) 13、(7,1) 14、10 15、平行、
19、A 20、A 21、(2, 5) 22、12
8、解:(1)A(2,1),B(2,4),C(4,3);
(2)画图,如第8题图②,
(2,1),B(2,4),C(4,3);
(3)是△ABC关于y轴对称图形.
16 解:过点P作PE⊥MN于的E,延长PE带P1 ,使PE= P1E,
则点P1就是点P关于直线MN的对称点.
连接OP、OP1,则有OP=OP1,∠POE=∠P1OE.
过点P作PD⊥y轴于D,P1作P1H⊥x轴于H.
∵MN是第一、三象限平分线,
∴∠DOE=∠HOE=45°.
∠1=∠2.
在Rt△PDO和Rt△P1HO中,
∵
∴Rt△PDO≌Rt△P1HO(AAS),
∴PD=P1H=3,OD= OH=4,
∴P1的坐标为(4,3).
17、解:(1)如图;
(2)原图坐标 变换后图形坐标
A(2,5)
B(2,5)
C(0,2)
D(3,0)
E(3,0)
(3)变换的图形和原图的关系是关于原点对称(或关于x轴对称).
18、解:(1)根据图形可得△ABC的顶点坐标分别为:
A(1,2),B(5,4),C(3,1);
(2)作出△ABC关于y轴的对称图形如图所示;
根据对称的性质可得的顶点坐标分别为:
(1,2),(5,4),(3,1);
(3)△ABC的面积为
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
