第二章 直线与圆的位置关系单元测试卷A(含解析)
文档属性
| 名称 | 第二章 直线与圆的位置关系单元测试卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-08 15:03:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2章 直线与圆的位置关系单元测试卷A
一.选择题(共10小题,3*10=30)
1.已知圆O的圆心到直线L的距离为3,若圆上有且只有2个点到L的距离为2,则半径r的取值范围是( )
A.r=3 B.1<r<3 C.1<r<5 D.1≤r≤5
2.在Rt△ABC中,∠C=90°,AC=3,BC=4.若以1为半径的圆在△ABC所在平面上运动,则这个圆与△ABC的三条边的公共点最多有( )
A.2个 B.3个 C.4个 D.5个
3.如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
A.2π B.4π C.2 D.4
4.如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
A.3+ B.2 C. D.
5.如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )
A.2 B.8 C.2 D.2
6.如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )
A.2 B. C. D.
7.如图,AB、CD是⊙O的两条平行弦,BE∥AC交CD于E,过A点的切线交DC延长线于P,若AC=3,则PC?CE的值是( )
A.18 B.6 C.6 D.9
8.如图,在以O为圆心的两个同心圆中,A为大圆上任意一点,过A作小圆的割线AXY,若AX?AY=4,则图中圆环的面积为( )
A.16π B.8π C.4π D.2π
9.如图,在Rt△ABC中,AC⊥BC,过C作CD⊥AB,垂足为D,若AD=3,BC=2,则△ABC的内切圆的面积为( )
A.π B.(4﹣2)π C.()π D.2π
10.若一直角三角形的斜边长为c,内切圆半径是r,则内切圆的面积与三角形面积之比是( )
A. B. C. D.
二.填空题(共10小题,3*10=30)
11.在Rt△ABC中,∠C=90°,AC=3,BC=4.若以C点为圆心,r为半径所作的圆与斜边AB只有一个公共点,则r的取值范围是 .
12.如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于 .
13.如图,正方形ABCD的边长为2,⊙O的直径为AD,将正方形沿EC折叠,点B落在圆上的F点,则BE的长为 .
14.如图四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠BCD=130°,则∠ADP= .
15.如图,四边形ABCD是正方形,以BC边为直径在正方形内作半圆O,再过顶点A作半圆O的切线(切点为F)交CD边于E,则sin∠DAE= .
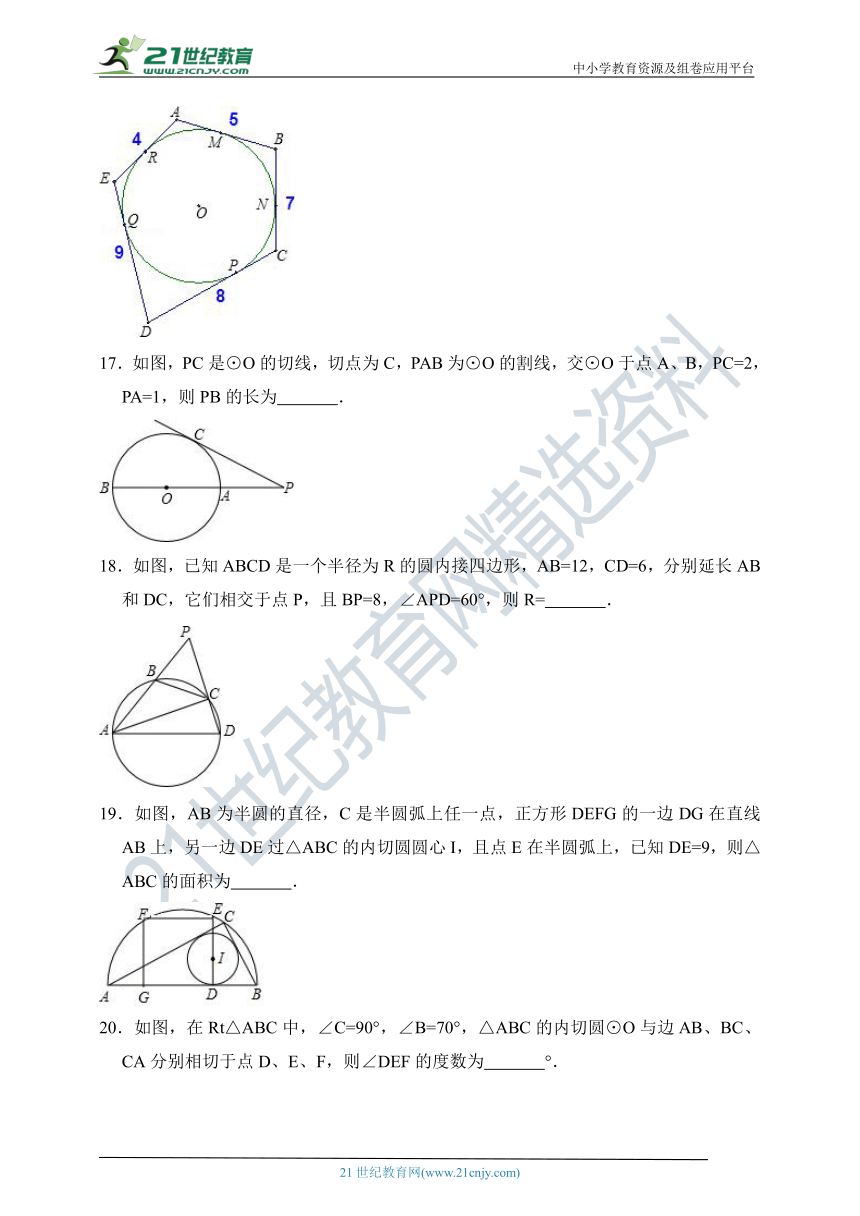
16.如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,则的值是 .
17.如图,PC是⊙O的切线,切点为C,PAB为⊙O的割线,交⊙O于点A、B,PC=2,PA=1,则PB的长为 .
18.如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R= .
19.如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为 .
20.如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
三.解答题(共4小题,40分)
21.(10分)如图,已知E为圆内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.求证:EF=FG.
22.(10分)如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为D.
(1)求证:CD与⊙O相切;
(2)若CD=2AD,⊙O的直径为10,求AB的长.
23.(10分)等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现△ABC以每秒2个单位的速度向右移动,同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大.
(1)当△ABC的边(BC边除外)与圆第一次相切时,点B移动了多少距离?
(2)若在△ABC移动的同时,⊙O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
(3)在(2)的条件下,是否存在某一时刻,△ABC与⊙O的公共部分等于⊙O的面积?若存在,求出恰好符合条件时两个图形移动了多少时间?若不存在,请说明理由.
24.(10分)如图,由矩形ABCD的顶点D引一条直线分别交BC及AB的延长线于F,G,连接AF并延长交△BGF的外接圆于H,连接GH,BH.
(1)求证:△DFA∽△HBG;
(2)过A点引圆的切线AE,E为切点,AE=3,CF:FB=1:2,求AB的长;
(3)在(2)的条件下,又知AD=6,求tan∠HBC的值.
参考答案与试题解析
1.解:以点O为圆心的圆上只有两点到直线l的距离为2,则两个交点在到直线l的距离是2的直线m上.
则直线m到圆心O的距离是:2+3=5或3﹣2=1.
圆O与直线m相交,因而该圆的半径r的取值范围是1<r<5.
故选:C.
2.解:如图所示:
以1为半径的圆在△ABC所在平面上运动,则这个圆与△ABC的三条边的公共点最多有4个,
故选:C.
3.解:当滚动到⊙O′与CA也相切时,切点为D,
连接O′C,O′B,O′D,OO′,
∵O′D⊥AC,
∴O′D=O′B.
∵O′C平分∠ACB,
∴∠O′CB=∠ACB=×60°=30°.
∵O′C=2O′B=2×2=4,
∴BC===2.
故选:C.
4.解:延长CD交⊙O于点E,过点O作OF⊥CE于点F,连接OC,
∵BA与⊙O相切,
∴由切割线定理可知:BA2=BC?BE,
∴BE=12,
∴CE=BE﹣BC=9,
∴由垂径定理可知:CF=CE=,
∴DF=CF﹣CD=,
∴由勾股定理可知:OF==,
∴由勾股定理可知:OC==,
故选:D.
5.解:连接OE和OC,且OC与EF的交点为M.
∵∠EDC=30°,
∴∠COE=60°.
∵AB与⊙O相切,
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,即△EOM为直角三角形.
在Rt△EOM中,EM=sin60°×OE=×2=,
∵EF=2EM,
∴EF=2.
故选:A.
6.解:线段PQ长度的最小值时,PQ为圆的直径,
如图,设QP的中点为F,圆F与AB的切点为D,连接FD、CF、CD,
∵圆F与AB相切,∴FD⊥AB,
∵AB=5,AC=4,BC=3,
∴∠ACB=90°,FC+FD=PQ,
∴CF+FD>CD,且PQ为圆F的直径,
∵当点F在直角三角形ABC的斜边AB的高上CD时,PQ=CD有最小值,即CD为圆F的直径,
且S△ABC=BC?CA=CD?AB,
∴CD==.
故选:B.
7.解:如图,连接AD、BC.
∵AB、CD是⊙O的两条平行弦,
∴弧AC=弧BD,
∴∠BCD=∠ADC.
∵过A点的切线交DC延长线于P,
∴∠PAC=∠D,
∴∠PAC=∠BCE.
∵BE∥AC交CD于E,
∴∠PCA=∠BEC,
∴△APC∽△CBE,
∴,
又AC=BE=3,
∴PC?CE=(3)2=18.
故选:A.
8.解:过点A作圆的切线AD,切点是D,
∵AD2=AX?AY,AX?AY=4,
∴AD=2,
∴圆环的面积=πAD2=4π.
故选:C.
9.解:∵在Rt△ABC中,AC⊥BC,过C作CD⊥AB
∴△ADC∽△CDB
∴CD2=AD?DB
∴CD2=3DB
Rt△CDB中,CB2=CD2+DB2
∴4=3DB+DB2
解得DB=1或DB=﹣4(舍去)
∴CB=2
∴AC=2
设△ABC内切圆半径为r,内心为O,连OA、OB、OC
由面积法可知
S△ABC=S△AOC+S△BOC+S△AOB
∴
∴r==
∴内切圆半径为π()2=(4﹣2)π
故选:B.
10.:设直角三角形的两条直角边是a,b,则有:
S=,
又∵r=,
∴a+b=2r+c,
将a+b=2r+c代入S=得:S=r=r(r+c).
又∵内切圆的面积是πr2,
∴它们的比是.
故选:B.
11.解:如图,∵BC>AC,
∴以C为圆心,r为半径所作的圆与斜边AB只有一个公共点.
根据勾股定理求得AB=5.
分两种情况:
(1)圆与AB相切时,即r=CD=3×4÷5=2.4;
(2)点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4.
∴3<r≤4或r=2.4.
12.解:OB是半径,AB是切线,
∵OB⊥AB,
∴∠ABO=90°,
∴sinA==,
∴∠A=30°,
∵OC=OB,BC∥OA,
∴∠OBC=∠BOA=60°,
∴△OBC是等边三角形,
因此S阴影=S扇形CBO==.
故答案为.
13.解:如图:连接OF,OC.
在△OCF和△OCD中,
∵OF=OD,OC=OC,CF=CD,
∴△OCF≌△OCD,
∴∠OFC=∠ODC=90°,
∴CF是⊙O的切线.
∵∠CFE=∠B=90°,
∴E,F,O三点共线.
∵EF=EB,
∴在△AEO中,AO=1,AE=2﹣BE,EO=1+BE,
∴(1+BE)2=1+(2﹣BE)2,
解得:BE=.
故答案是:.
14.解:连接BD,
∵四边形ABCD内接于⊙O,∠BCD=130°,
∴∠BAD=50°,
∵AB为直径,
∴∠ADB=90°,
∴∠ABD=∠40°
∵PD切⊙O于D,
∴∠ADP=∠ABD=40°,
故答案为:40°.
15.解:设正方形ABCD的边长为4a,EC=x,
∵AF为半圆O的切线,
∴AF=AB=4a,EC=EF=x,
在Rt△ADE中,DE=4a﹣x,AE=4a+x,
∴AE2=AD2+DE2,即(4a+x)2=(4a)2+(4a﹣x)2,
解得x=a,
∴AE=5a,DE=3a,
在Rt△ADE中,sin∠DAE===.
故答案为.
16.
解:设AM=x,BM=y,
∵圆O内切于五边形ABCDE,
∴AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,AR=AM,
∴BN=y,
∵AB=5,
∴x+y=5,
∵BC=7,
∴CN=CP=7﹣y,
∵CD=8,∴DQ=DP=y+1,
∵DE=9,
∴EQ=ER=8﹣y,
∵EA=4,
∴AR=AM=y﹣4,
∴y﹣4=x,
∴,
解得:,
∴AM=,MB=,
∴==;
故答案为:
17.解:由切割线定理知:PC2=PA?PB,
故PB=PC2÷PA=4÷1=4,
即PB的长为4.
18.解:由切割线定理得PB?PA=PC?PD,则有
8×20=PC(PC+6).
解得PC=10.
在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.
从而AD是圆的直径.由勾股定理,得
AD2=AC2+CD2=(PA2﹣PC2)+CD2=202﹣102+62=336.
∴AD==4
∴R=AD=2.
故答案为2.
19.解:设⊙I切AC与M,切BC于N,半径为r,
则AD=AM,CM=CN=r,BD=BN,r=(AC+BC﹣AB),
∵AB为半圆的直径,
∴∠ACB=90°,
∴AB2=AC2+BC2,
∴AD?DB=AM?BN=(AC﹣r)(BC﹣r)=[AC﹣(AC+BC﹣AB)][BC﹣(AC+BC﹣AB)]
=(AC﹣BC+AB)(AB+BC﹣AC)=(AB2﹣AC2﹣BC2+2AC?BC)=AC?BC,
由射影定理得AD?DB=DE2=81,
∴S△ABC=AC?BC=81,
故答案为:81.
20.解:连接DO,FO,
∵在Rt△ABC中,∠C=90°,∠B=70°
∴∠A=20°,
∵内切圆O与边AB、BC、CA分别相切于点D、E、F,
∴∠ODA=∠OFA=90°,
∴∠DOF=160°,
∴∠DEF的度数为80°.
21.解:连接EF,
∵EF∥CB,
∴∠BCD=∠FED,又∠BCD=∠BAD,
∴∠BCD=∠FED,又∠EFD=∠EFD,
∴△FED∽△FAE,
∴=,
∴EF2=FD?FA,
∵FG切圆于G,
∴GF2=FD?FA,
∴EF=FG.
22.(1)证明:连接OC.
∵OC=OA,
∴∠OAC=∠OCA.
∵AC平分∠PAE,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC.
∵CD⊥PA,
∴∠ADC=∠OCD=90°,
即 CD⊥OC,点C在⊙O上,
∴CD是⊙O的切线.
(2)解:过O作OM⊥AB于M.
即∠OMA=90°,
∵∠MDC=∠OMA=∠DCO=90°,
∴四边形DMOC是矩形,
∴OC=DM,OM=CD.
∵CD=2AD,
∴设AD=x,则DC=OM=2x,AM=DM﹣DA=5﹣x,
∵在Rt△AMO中,∠AMO=90°,根据勾股定理得:AO2=AM2+OM2.
∴52=(5﹣x)2+(2x)2,
解得 x1=0(不合题意,舍去),x2=2.
则 AM=DM﹣DA=5﹣x=3,
∵OM⊥AB,
∴AB=2AM=6.
23.
解:(1)设第一次相切时,△ABC移至△A′B′C′处,A′C′与⊙O切于点E,连OE并延长,
交B′C′于F.
设⊙O与直线l切于点D,连OD,则OE⊥A′C′,OD⊥直线l.
由切线长定理可知C’E=C′D,设C′D=x,则C′E=x,易知C′F=x.
∴x+x=1,
∴x=﹣1,
∴CC’=5﹣1﹣(﹣1)=5﹣.
∴点C运动的时间为(5﹣)÷(2+0.5)=2﹣.
∴点B运动的距离为(2﹣)×2=4﹣.
(2)∵△ABC与⊙O从开始运动到最后一次相切时,是AB与圆相切,且圆在AB的左侧,故路程差为6,速度差为1,
∴从开始运动到最后一次相切的时间为6秒.
(3)∵△ABC与⊙O从开始运动到第二次相切时,路程差为4,速度差为1,
∴从开始运动到第二次相切的时间为4秒,此时△ABC移至△A″B″C″处,
A″B″=1+4×=3.
连接B”O并延长交A″C″于点P,易证B″P⊥A″C″,且OP=﹣=<1.
∴此时⊙O与A″C″相交,
∴不存在.
24.证明:(1)∵∠HBG=∠HFG,∠HFG=∠AFD,
∴∠HBG=∠AFD.
∵∠BHG=∠BFG=∠CFD=∠ADG,
∴△DFA∽△HBG.(4分)
(2)∵CD∥AB,CD=AB,
∴.
即AG=3AB.
∵AE为⊙O的切线,
∴AE2=AB?AG.
∴AB=3.(8分)
(3)∵AD=BC=6,CF:FB=1:2,
∴CF=2,BF=4.
∵∠ABC=90°,
∴AF=.
∵AE2=AF?AH,
∴AH=FH=AH﹣AF=.
∴FH=AH﹣AF=.
∵∠FBG=90°,FG=,
∵FG为圆的直径,
∴HG=.
∴tan∠HGF==.
∵∠HBC=∠HGF
∴tan∠HBC=(12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
