第二章 直线与圆的位置关系单元测试卷B(含解析)
文档属性
| 名称 | 第二章 直线与圆的位置关系单元测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-08 19:00:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2章直线与圆的位置关系单元测试卷B
一.选择题(共10小题,3*10=30)
1.已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.已知⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,那么直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
3.如图,AB是⊙O的切线,A为切点,连接OB交⊙O于点C.若OA=3,tan∠AOB=,则BC的长为( )
A.2 B.3 C.4 D.5
4.如图,BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
5.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )
A.4 B.2 C.3 D.2.5
6.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )
A.随圆的大小变化而变化,但没有最值
B.最大值为4.8
C.有最小值
D.为定值
7.如图,P为半⊙O直径BA延长线上一点,PC切半⊙O于C,且PA:PC=2:3,则sin∠ACP的值为( )
A. B. C. D.无法确定
8.如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为( )
A. B. C. D.2
9.已知直角三角形两边长x,y满足=0,则直角三角形内切圆半径为( )
A. B. C.或 D.
10.如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
A.1 B.2 C.2﹣2 D.4﹣2
二.填空题(共10小题,3*10=30)
11.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB有两个交点,则R的取值范围是 .
12.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°,CD是⊙O的切线:若⊙O的半径为2,则图中阴影部分的面积为 .
13.如图,AB是⊙O的直径,点D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.若⊙O的半径为2,TC=,则图中阴影部分的面积是 .
14.如图,已知AB是⊙O的直径,PC切⊙O于点C,∠PCB=35°,则∠B等于 度.
15.如图,已知PA、PB分别切⊙O于点A、B,∠P=90°,PA=3,那么⊙O的半径长是 .
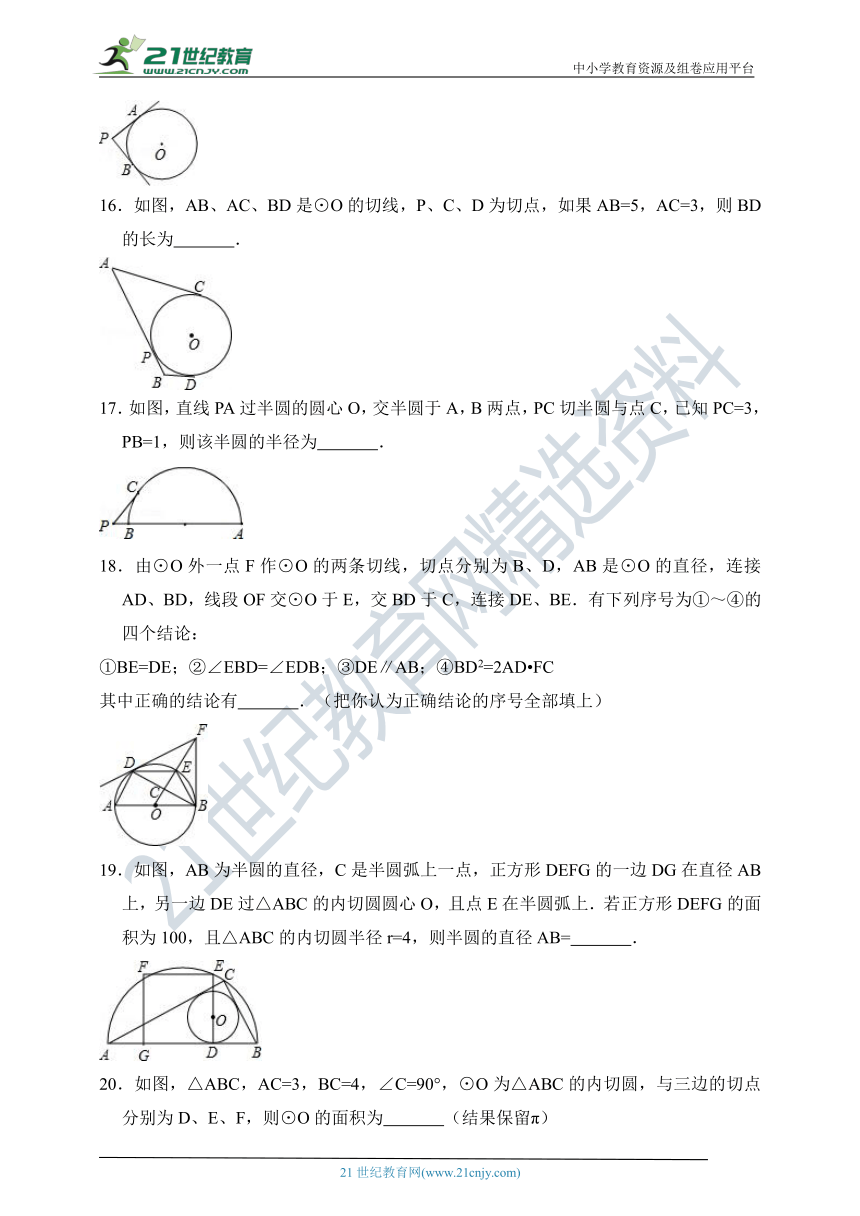
16.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为 .
17.如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为 .
18.由⊙O外一点F作⊙O的两条切线,切点分别为B、D,AB是⊙O的直径,连接AD、BD,线段OF交⊙O于E,交BD于C,连接DE、BE.有下列序号为①~④的四个结论:
①BE=DE;②∠EBD=∠EDB;③DE∥AB;④BD2=2AD?FC
其中正确的结论有 .(把你认为正确结论的序号全部填上)
19.如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆弧上.若正方形DEFG的面积为100,且△ABC的内切圆半径r=4,则半圆的直径AB= .
20.如图,△ABC,AC=3,BC=4,∠C=90°,⊙O为△ABC的内切圆,与三边的切点分别为D、E、F,则⊙O的面积为 (结果保留π)
三.解答题(共4小题,40分)
21.(10分)如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于Q,过Q的⊙O的切线交OA的延长线于R.求证:RP=RQ.
22.(10分)如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+,BC=2,求⊙O的半径.
23.(10分)直角坐标系中,已知A(1,0),以点A为圆心画圆,点M(4,4)在⊙A上,直线y=﹣x+b过点M,分别交x轴、y轴于B、C两点.
(1)①填空:⊙A的半径为 ,b= .(不需写解答过程)
②判断直线BC与⊙A的位置关系,并说明理由.
(2)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求的值.
(3)若点P在⊙A上,点Q是y轴上一点且在点C下方,当△PQM为等腰直角三角形时,直接写出点Q的坐标.
24.(10分)如图,P为⊙O外的一点,过点P作⊙O的两条割线,分别交⊙O于A、B和C、D,且AB是⊙O的直径,已知PA=OA=4,AC=CD.
(1)求DC的长;
(2)求cosB的值.
参考答案与试题解析
1.解:∵⊙O的半径为3,圆心O到直线L的距离为2,
∵3>2,即:d<r,
∴直线L与⊙O的位置关系是相交.
故选:A.
2.解:∴⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,
∴3.5<4,
∴直线l与⊙O的位置关系是相交,
故选:A.
3.解:∵OA=3,tan∠AOB=,
∴OB=5,
∴CB=OB﹣OC=5﹣3=2,
故选:A.
4.解:如图,连接OA、OB,
∵BM是⊙O的切线,
∴∠OBM=90°,
∵∠MBA=140°,
∴∠ABO=50°,
∵OA=OB,
∴∠ABO=∠BAO=50°,
∴∠AOB=80°,
∴∠ACB=∠AOB=40°,
故选:A.
5.解:连接DO,
∵PD与⊙O相切于点D,
∴∠PDO=90°,
∵∠C=90°,
∴DO∥BC,
∴△PDO∽△PCB,
∴===,
设PA=x,则=,
解得:x=4,
故PA=4.
故选:A.
6.解:由题意得,AB2=AC2+BC2,
∴△ABC为RT△,即∠C=90°,可知EF为圆的直径,
设圆与AB的切点为D,连接CD,
当CD⊥AB,即CD是圆的直径的时候,EF长度最小.
故选:C.
7.解:如图,连接BC,
由已知条件得,△PAC∽△PBC,于是==,
设AC=2k,BC=3k,由∠ACB=90°得,AB=,
∴sin∠ACP=sin∠ABC===.
故选:B.
8.解:∵AC是圆O1的切线,
∴∠CAB=∠D,
又∵∠C=∠C,
∴△ACD∽△BCA,
∴
∴AC2=BC?CD,
∵AB=2,BD=3,BC=5,
∴AC2=40,AC=2,
∵,
∴AD=
故选:C.
9.解:∵|x2﹣4|+=0,
∴x2﹣4=0,y2﹣6y+9=0,
解得:x=±2,y=3,
∵x、y表示直角三角形的两边长,
∴x=2,y=3,
设内切圆O的半径是R,与AC、BC、AB分别切于F、D、E,连接OA、OB、OC、OD、OE、OF,
①AC=2,BC=3时,由勾股定理得:AB==,
由三角形的面积公式得:S△ABC=S△ACO+S△BCO+S△ABO,
∴AC×BC=AC×OF+BC×OD+AB×OE,
即2×3=2R+3R+R,
解得:R=,
②AC=2,AB=3时,由勾股定理得:BC==
由三角形的面积公式得:S△ABC=S△ACO+S△BCO+S△ABO,
∴AC×BC=AC×OF+BC×OD+AB×OE,
即2×=2R+3R+R,
解得:R=.
故选:C.
10.解:如图,
连接PF,QF,PC,QC,
∵P、Q两点分别为△ACF、△CEF的内心,
∴PF是∠AFC的角平分线,FQ是∠CFE的角平分线,
∴∠PFC=∠AFC=30°,∠QFC=∠CFE=30°,
∴∠PFC=∠QFC=30°,
同理,∠PCF=∠QCF
∴PQ⊥CF,
∴△PQF是等边三角形,
∴PQ=2PG;
易得△ACF≌△ECF,且内角是30°,60°,90°的三角形,
∴AC=2,AF=2,CF=2AF=4,
∴S△ACF=AF×AC=×2×2=2,
过点P作PM⊥AF,PN⊥AC,PQ交CF于G,
∵点P是△ACF的内心,
∴PM=PN=PG,
∴S△ACF=S△PAF+S△PAC+S△PCF
=AF×PM+AC×PN+CF×PG
=×2×PG+×2×PG+×4×PG
=(1++2)PG
=(3+)PG
=2,
∴PG==﹣1
∴PQ=2PG
=2(﹣1)
=2﹣2.
故选:C.
11.解:如图,
∵BC>AC,
∴以C为圆心,R为半径所作的圆与斜边AB有两个交点,则圆的半径应大于CD,小于或等于AC,
由勾股定理知,AB==5.
∵S△ABC=AC?BC=CD?AB=×3×4=×5?CD,
∴CD=2.4,
即R的取值范围是2.4<R≤3.
12.
解:连接OC,
∵AC=CD,∠ACD=120°,
∴∠CAD=∠D=30°,
∵DC切⊙O于C,
∴OC⊥CD,
∴∠OCD=90°,
∴∠COD=60°,
在Rt△OCD中,∠OCD=90°,∠D=30°,OC=2,
∴CD=2,
∴阴影部分的面积是S△OCD﹣S扇形COB=×2×2﹣=2﹣π,
故答案为:2﹣π.
13.解:连接OT、OD、DT,过O作OM⊥AD于M,
∵OA=OT,AT平分∠BAC,
∴∠OTA=∠OAT,∠BAT=∠CAT,
∴∠OTA=∠CAT,
∴OT∥AC,
∵PC⊥AC,
∴OT⊥PC,
∵OT为半径,
∴PC是⊙O的切线,
∵OM⊥AC,AC⊥PC,OT⊥PC,
∴∠OMC=∠MCT=∠OTC=90°,
∴四边形OMCT是矩形,
∴OM=TC=,
∵OA=2,
∴sin∠OAM=,
∴∠OAM=60°,
∴∠AOM=30°
∵AC∥OT,
∴∠AOT=180°﹣∠OAM=120°,
∵∠OAM=60°,OA=OD,
∴△OAD是等边三角形,
∴∠AOD=60°,
∴∠TOD=120°﹣60°=60°,
∵PC切⊙O于T,
∴∠DTC=∠CAT=∠BAC=30°,
∴tan30°==,
∴DC=1,
∴阴影部分的面积是S梯形OTCD﹣S扇形OTD=×(2+1)×﹣=.
故答案为:.
14.解:∵PC切⊙O于点C,∠PCB=35°,
∴∠A=∠PCB=35°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∴35°+∠B=90°,
解得∠B=55°.
故答案为:55.
15.
解:连接OA、OB,
则OA=OB(⊙O的半径),
∵PA、PB分别切⊙O于点A、B,
∴PA=PB,∠OAP=∠OBP=90°,
已知∠P=90°,
∴∠AOB=90°,
∴四边形APBO为正方形,
∴OA=OB=PA=3,
则⊙O的半径长是3,
故答案为:3.
16.解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=5﹣3=2.
故答案为:2.
17.解:∵PC切半圆与点C,
∴PC2=PA?PB,
即PA=9,
则AB=9﹣1=8,
则圆的半径是4.
故答案为4.
18.解:∵BF,DF是⊙O的两条切线
∴OF是∠DFB的角平分线,DF=FB,FO⊥BD,CD=CB
∴=
∴BE=DE(①正确)
∵=
∴∠EBD=∠EDB(②正确)
∵FB切⊙O于B
∴FB⊥OB
∵BC⊥OF
∵BC2=OC?FC
∴(BD)2=OC?CE
∵OC为△ABD的中位线
∴OC=AD
∴(BD)2=AD?CE
∴BD2=2AD?FC(④正确)
故其中正确的结论有①②④.
19.解:∵正方形DEFG的面积为100,
∴正方形DEFG边长为10.
连接EB、AE,OI、OJ,
∵AC、BC是⊙O的切线,
∴CJ=CI,∠OJC=∠OIC=90°,
∵∠ACB=90°,
∴四边形OICJ是正方形,且边长是4,
设BD=x,AD=y,则BD=BI=x,AD=AJ=y,
在Rt△ABC中,由勾股定理得(x+4)2+(y+4)2=(x+y)2①;
在Rt△AEB中,
∵∠AEB=90°,ED⊥AB,
∴△ADE∽△BDE∽△ABE,
∴ED2=AD?BD,即102=x?y②.
解①、②得x+y=21,即半圆的直径AB=21.
故答案为:21.
20.解:连接OE、OF,
∵AC=3,BC=4,∠C=90°,
∴AB=5,
∵⊙O为△ABC的内切圆,D、E、F为切点,
∴FB=DB,CE=CF,AD=AF,
OE⊥BC,OF⊥AC,
又∵∠C=90°,OF=OE,
∴四边形ECFO为正方形,
∴设OE=OF=CF=CE=x,
∴BE=4﹣x,FA=3﹣x;
∴DB=4﹣x,AD=3﹣x,
∴3﹣x+4﹣x=5,
解得:x=1,
则⊙O的面积为:π.
故答案为:π.
21.证明:连接OQ,
∵RQ是⊙O的切线,
∴OQ⊥QR,
∴∠OQB+∠BQR=90°.
∵OA⊥OB,
∴∠OPB+∠B=90°.
又∵OB=OQ,
∴∠OQB=∠B.
∴∠PQR=∠BPO=∠RPQ.
∴RP=RQ.
22.(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:过点C作CE⊥AB于点E.
在Rt△BCE中,∠B=60°,BC=2,
∴BE=BC=,CE=3,
∵AB=4+,
∴AE=AB﹣BE=4,
∴在Rt△ACE中,AC==5,
∴AP=AC=5.
∴在Rt△PAO中,OA=,
∴⊙O的半径为.
23.(1)①解:连接AM,过M作MQ⊥x轴于Q,
则AQ=4﹣1=3,MQ=4,
由勾股定理得:AM==5,
把M(4,4)代入y=﹣x+b得:4=﹣×4+b,
∴b=7,
故答案为:5,7.
②解:相切,
理由是:连接AF,
y=﹣x+7,
当x=0时,y=7,∴C(0,7),OC=7,
当y=0时,0=﹣x+7,
∴x=,
∴B(,0),OB=,
∴BQ=OB﹣OQ=﹣4=,AQ=4﹣1=3,MQ=4,
∴==,=,
∴=,
∵∠MQA=∠MQB,
∴△AMQ∽△MBQ,
∴∠MAQ=∠BMQ,
∵∠MAQ+∠AMQ=90°,
∴∠AMQ+∠BMQ=90°,
∴AM⊥BC,
∴直线BC与⊙A的位置关系是相切.
(2)解:连接AC,
在△COB中,由勾股定理得:BC==,
同理AC=5,
∵AM=5,由勾股定理得:CM=5,
设EG=a,
∵EF⊥BC,
∴∠FEB=∠COB=90°,
∵∠OBC=∠OBC,
∴△BEG∽△BOC,
∴=,
即=,
∴BE=a,
∴根据切线长定理得:EM=EF=BC﹣BE﹣CM=﹣a﹣5,
∵EF⊥CB,AF⊥EF,
∴AF∥BC,
∴△AFG∽△BEG,
∴=,
∴=,
∴FG=,
∵BE+EM+CM=BC,
∴a+a++5=,
a=,
EG=,FG=,
∴==3.
(3)解:①当∠PQM=90°时,MQ=PQ,由对称性M,P关于X轴对称,
所以Q,O重合,Q(0,0);
②当∠PMQ=90°,MQ=MP,作MD⊥x,MH⊥y,
可得△MHQ≌△MDP,
即P是圆与x正半轴交点
从而Q(0,2);
③当∠QPM=90°时,分两种情况:
第一情况:P在y的左方,如图,设P(m,n),Q(0,b)可得:
①4﹣m=n﹣b,②4﹣n=﹣m,③(1﹣m)2+n2=52,
解方程组得,b=2,b=﹣8(b=2也符合条件,虽与②中b同,但直角不同),
第二情况:P在y的右方,同理得:
①m﹣4=n﹣b,②4﹣n=m,③(1﹣m)2+n2=52,
解方程组得,b=3+(舍),b=3﹣.
综合上述:Q的坐标是(0,0)或(0,2)或(0,﹣8)或(0,3﹣).
24.解:(1)连接OC、BC、AD,
∵AC=DC,
∴∠CDA=∠CAD,
又∵∠CAD=∠CBD,∠CDA=∠ACB,
∴∠CBD=∠CBA,
∴∠DBA=2∠CBA,
又∵∠COA=2∠CBA,
∴∠DBA=∠COA,
∴OC∥BD,
设CD=x,
∴CP:CD=OP:OB,
∴CP:x=8:4,
∴CP=2x,
∴CP?PD=AP?BP,
∴2x?(2x+x)=4×(4+4+4),
∴x=2,
即CD=2;
(2)∵OC∥BD,
∴OC:BD=OP:OB,
∴4:BD=(4+4):4,
∴BD=6,
∴在Rt△ABD中,cosB===.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
