九年级上册第三章圆的基本性质3.2 图形的旋转 同步练习(含答案)
文档属性
| 名称 | 九年级上册第三章圆的基本性质3.2 图形的旋转 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 303.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-13 16:09:32 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第2节)
一、单选题(共10题;共20分)
1.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
2.如图,将△ABC绕点C顺时针方向旋转40°得△A’CB’,若AC⊥A’B’,则∠BAC等于(????)
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
3.已知点A的坐标为,O为坐标原点,连结OA,将线段OA绕点O按逆时针方向旋转90°得OA1 , 则点A1的坐标为(??)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
4.如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.?45°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?90°
5.如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( )
A.???????????????????B.???????????????????C.???????????????????D.?
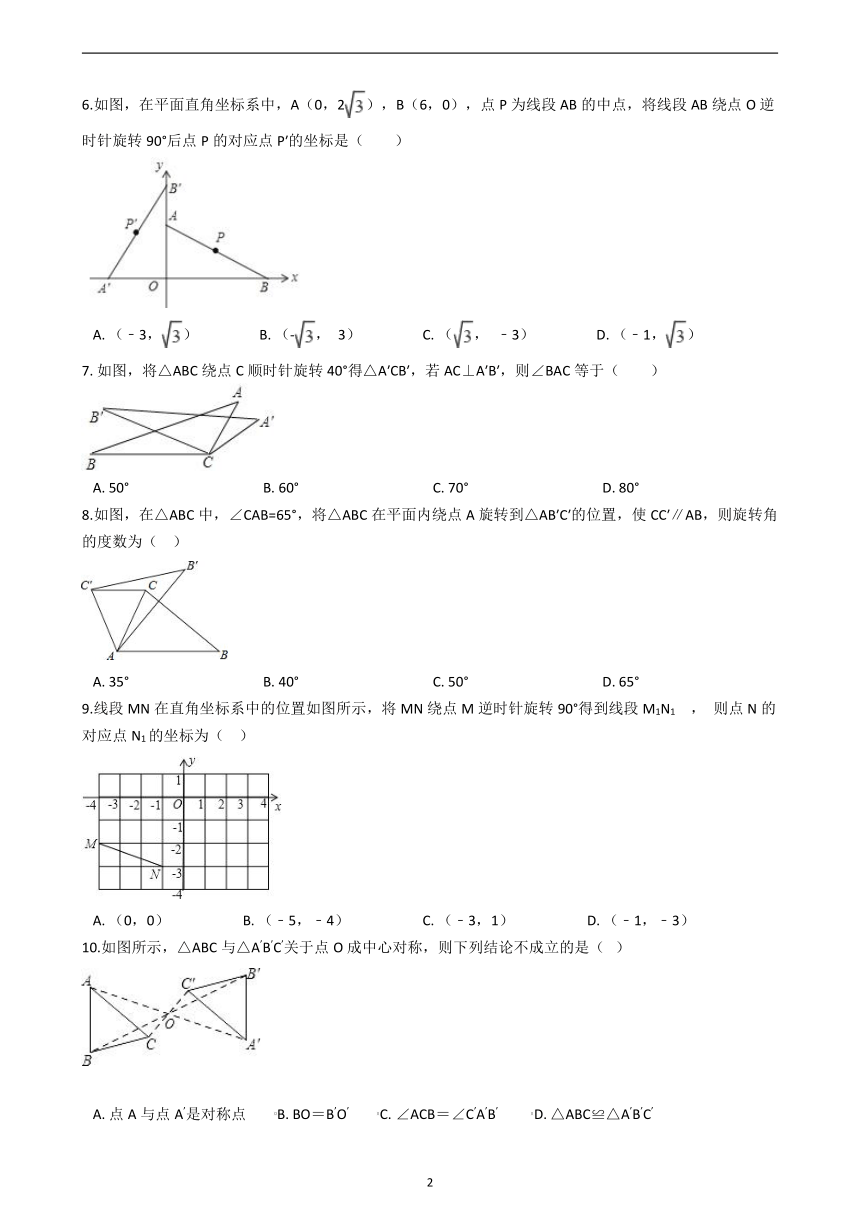
6.如图,在平面直角坐标系中,A(0,2),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
A.?(﹣3,)??????????????????B.?(-, 3)??????????????????C.?(, ﹣3)??????????????????D.?(﹣1,)
7.?如图,将△ABC绕点C顺时针旋转40°得△A′CB′,若AC⊥A′B′,则∠BAC等于( )
?
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
8.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为(?? )
A.?35°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?65°
9.线段MN在直角坐标系中的位置如图所示,将MN绕点M逆时针旋转90°得到线段M1N1 , 则点N的对应点N1的坐标为(?? )
A.?(0,0)?????????????????????B.?(﹣5,﹣4)?????????????????????C.?(﹣3,1)?????????????????????D.?(﹣1,﹣3)
10.如图所示,△ABC与△A’B’C’关于点O成中心对称,则下列结论不成立的是(???)
A.?点A与点A’是对称点????????B.?BO=B’O’????????C.?∠ACB=∠C’A’B’ ????????D.?△ABC≌△A’B’C’
二、填空题(共6题;共6分)
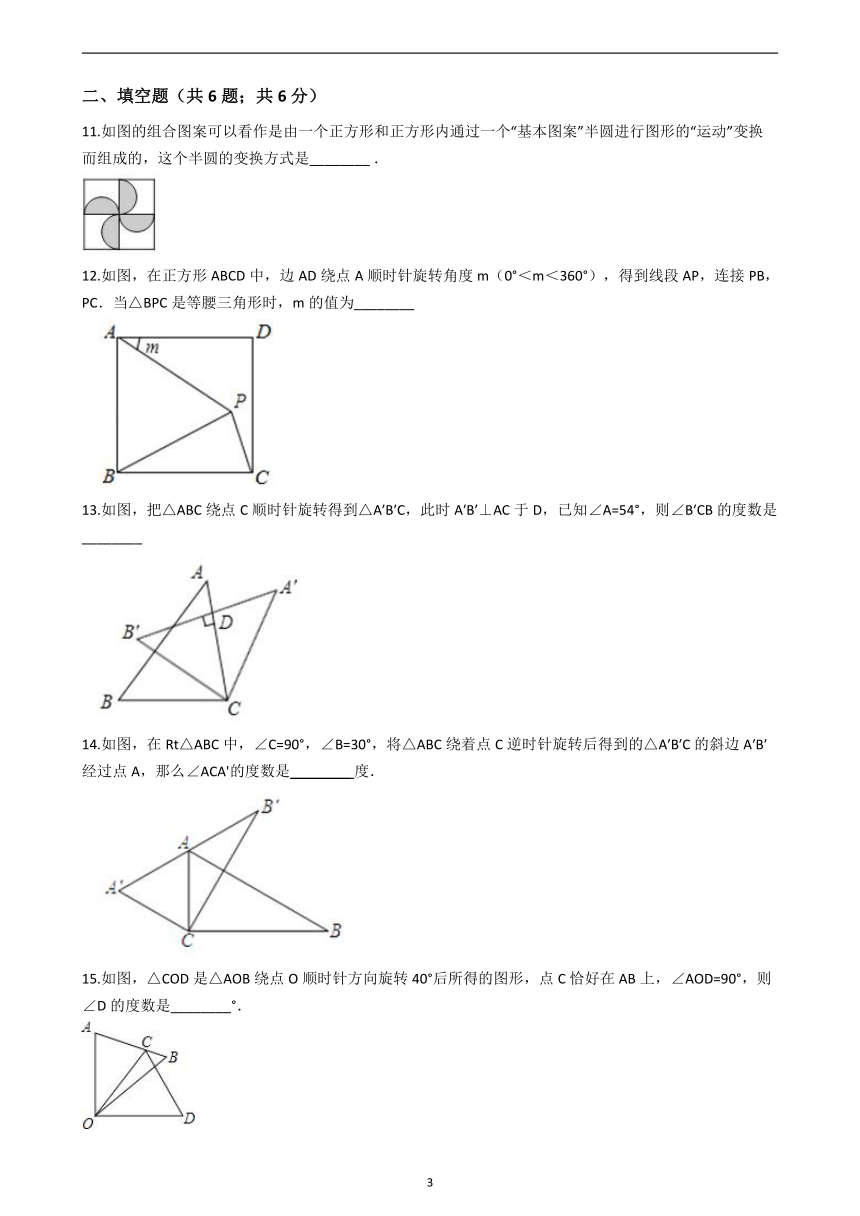
11.如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是________?.
12.如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为________?
13.如图,把△ABC绕点C顺时针旋转得到△A′B′C,此时A′B′⊥AC于D,已知∠A=54°,则∠B′CB的度数是________?
14.如图,在Rt△ABC中,∠C=90°,∠B=30°,将△ABC绕着点C逆时针旋转后得到的△A′B′C的斜边A′B′经过点A,那么∠ACA'的度数是________?度.
15.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠D的度数是________°.
16.如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1 , 则∠A1OB=________?.
三、解答题(共4题;共20分)
17.如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2 , 请画出△A2B2C2;
(3)若点O的坐标为(0,0),点B的坐标为(2,3);写出△A1B1C1与△A2B2C2的对称中心的坐标
18.如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.
(1)请直接写出:∠A的度数
(2)请求出线段OD扫过的面积.
19.如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),且△A1B1C1与△ABC关于原点O成中心对称.
(1)画出△A1B1C1 , 并写出A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对称点P′(a+3,b+1),请画出平移后的△A2B2C2 .
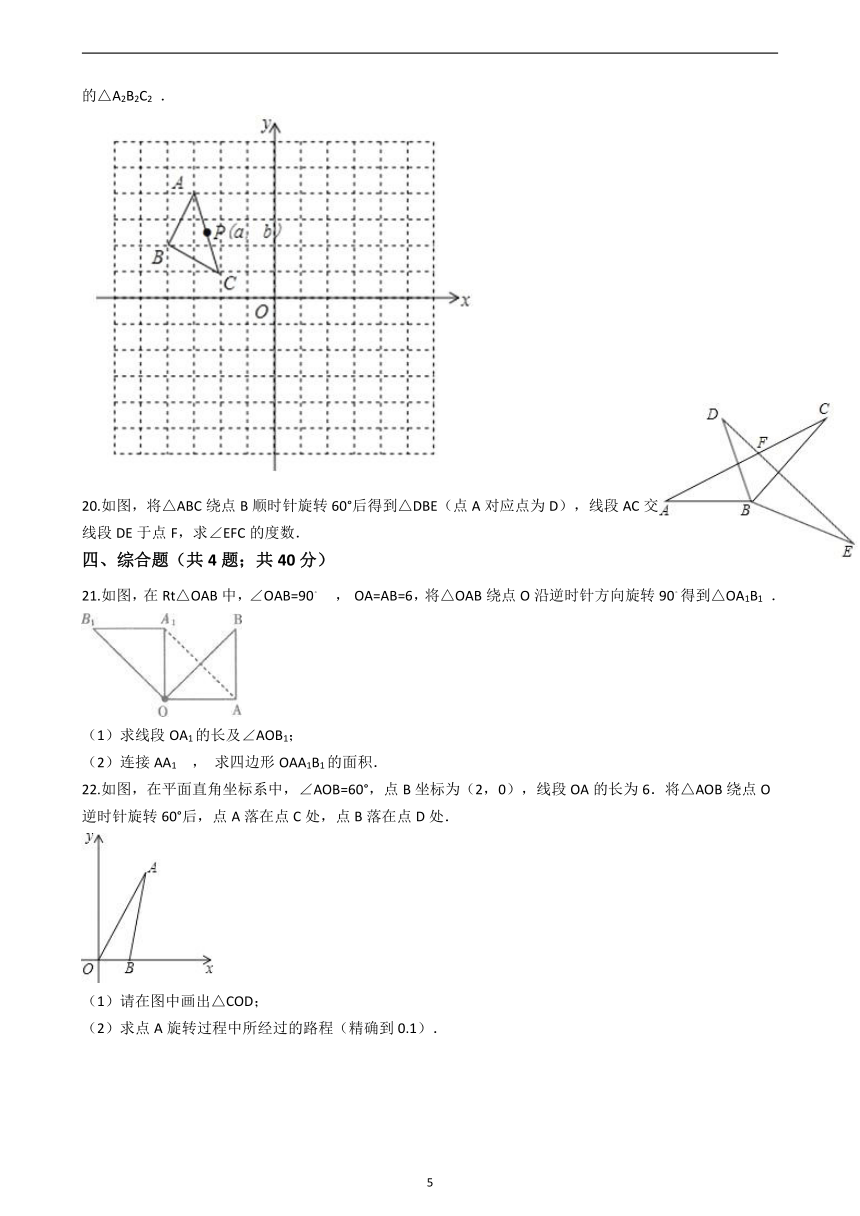
20.如图,将△ABC绕点B顺时针旋转60°后得到△DBE(点A对应点为D),线段AC交线段DE于点F,求∠EFC的度数.
四、综合题(共4题;共40分)
21.如图,在Rt△OAB中,∠OAB=90。 , OA=AB=6,将△OAB绕点O沿逆时针方向旋转90。得到△OA1B1 .
(1)求线段OA1的长及∠AOB1;
(2)连接AA1 , 求四边形OAA1B1的面积.
22.如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6.将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
(1)请在图中画出△COD;
(2)求点A旋转过程中所经过的路程(精确到0.1).
23.在△ABC中,AB=AC=5,cos∠ABC= ,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.
24.在方格纸上建立如图所示的平面直角坐标系,将△ABO绕点O按顺时针方向旋转90°,得△A′B′O.
(1)画出旋转后的图形;
(2)写出点A′,B′的坐标.
答案
一、单选题
1.D 2.A 3.A 4.D 5.A 6.B 7.A 8.C 9.C 10.C
二、填空题
11.旋转 12.30°或60°或150°或300° 13.36° 14.60 15.60 16.70°
三、解答题
17.解:(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示;
(3)旋转中心(﹣3,0).
故答案为:(﹣3,0).
18.解:在Rt△DOC,∠OCD=90°,OD=6,OC=3,
∴sin∠D=.
∴∠D=30°,
由旋转的性质可知:∠A=∠D=30°.
(2)在Rt△DOC,∠OCD=90°,∠D=30°,
∴∠DOC=60°,
∴∠AOD=180°﹣60°=120°,
∴线段OD扫过的面积为.
19.解:(1)如图所示:
A1的坐标是(3,﹣4);
(2)△A2B2C2是所求的三角形.
20.解:如图,
∵△ABC绕点B顺时针旋转60°后得到△DBE,
∴△ABC≌△DBE,
∴∠A=∠D,
又∵∠1=∠2,
∴∠DFA=∠ABD=60°,
∴∠EFC=∠DFA=60°
四、综合题
21.(1)解? :∵OA=AB=6,将△OAB绕点0沿逆时针方向旋转90°得到△OA1B1 ,
∴OA1=OA=6cm,
∵在Rt△OAB中,∠OAB=90°,OA=AB,
∴∠AOB=∠B=45°,
∵将△OAB绕点0沿逆时针方向旋转90°得到△OA1B1 ,
∴∠AOA1=90°,∠B1OA1=∠BOA=45°,
∴∠AOB1=90°+45°=135°,
(2)解 :∵将△OAB绕点0沿逆时针方向旋转90°得到△OA1B1,∠OAB=90°,OA=AB=6,
∴△AOB≌△A1OB1 ,
∴S四边形OAA1B1=2S△AOB=2××6×6=36cm2
22.(1)解:如图,△COD为所作;
(2)解:点A旋转过程中所经过的路程长= =2π≈6.3.
23.(1)解:①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图①:
∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC= ,AB=5,
∴BF=3,
∴BC=6,
∴B1C=BC=6,
∵CE⊥AB,
∴BE=B1E= ,
∴BB1= ,CE= ,
∴AB1= ,
∴△AB1C的面积为:
(2)解:如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1 , EF1有最小值,
此时在Rt△BFC中,CF= ,
∴CF1= ,
∴EF1的最小值为 ;
如图,以C为圆心BC为半径画圆交BC的延长线于F1 , EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为
24.(1)解:如图,△OA′B′即为旋转后的三角形
(2)解:由图可知,A′(2,3),B′(4,1).
(
1
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第2节)
一、单选题(共10题;共20分)
1.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
2.如图,将△ABC绕点C顺时针方向旋转40°得△A’CB’,若AC⊥A’B’,则∠BAC等于(????)
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
3.已知点A的坐标为,O为坐标原点,连结OA,将线段OA绕点O按逆时针方向旋转90°得OA1 , 则点A1的坐标为(??)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
4.如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.?45°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?90°
5.如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( )
A.???????????????????B.???????????????????C.???????????????????D.?
6.如图,在平面直角坐标系中,A(0,2),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
A.?(﹣3,)??????????????????B.?(-, 3)??????????????????C.?(, ﹣3)??????????????????D.?(﹣1,)
7.?如图,将△ABC绕点C顺时针旋转40°得△A′CB′,若AC⊥A′B′,则∠BAC等于( )
?
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
8.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为(?? )
A.?35°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?65°
9.线段MN在直角坐标系中的位置如图所示,将MN绕点M逆时针旋转90°得到线段M1N1 , 则点N的对应点N1的坐标为(?? )
A.?(0,0)?????????????????????B.?(﹣5,﹣4)?????????????????????C.?(﹣3,1)?????????????????????D.?(﹣1,﹣3)
10.如图所示,△ABC与△A’B’C’关于点O成中心对称,则下列结论不成立的是(???)
A.?点A与点A’是对称点????????B.?BO=B’O’????????C.?∠ACB=∠C’A’B’ ????????D.?△ABC≌△A’B’C’
二、填空题(共6题;共6分)
11.如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是________?.
12.如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为________?
13.如图,把△ABC绕点C顺时针旋转得到△A′B′C,此时A′B′⊥AC于D,已知∠A=54°,则∠B′CB的度数是________?
14.如图,在Rt△ABC中,∠C=90°,∠B=30°,将△ABC绕着点C逆时针旋转后得到的△A′B′C的斜边A′B′经过点A,那么∠ACA'的度数是________?度.
15.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠D的度数是________°.
16.如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1 , 则∠A1OB=________?.
三、解答题(共4题;共20分)
17.如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2 , 请画出△A2B2C2;
(3)若点O的坐标为(0,0),点B的坐标为(2,3);写出△A1B1C1与△A2B2C2的对称中心的坐标
18.如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.
(1)请直接写出:∠A的度数
(2)请求出线段OD扫过的面积.
19.如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),且△A1B1C1与△ABC关于原点O成中心对称.
(1)画出△A1B1C1 , 并写出A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对称点P′(a+3,b+1),请画出平移后的△A2B2C2 .
20.如图,将△ABC绕点B顺时针旋转60°后得到△DBE(点A对应点为D),线段AC交线段DE于点F,求∠EFC的度数.
四、综合题(共4题;共40分)
21.如图,在Rt△OAB中,∠OAB=90。 , OA=AB=6,将△OAB绕点O沿逆时针方向旋转90。得到△OA1B1 .
(1)求线段OA1的长及∠AOB1;
(2)连接AA1 , 求四边形OAA1B1的面积.
22.如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6.将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
(1)请在图中画出△COD;
(2)求点A旋转过程中所经过的路程(精确到0.1).
23.在△ABC中,AB=AC=5,cos∠ABC= ,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.
24.在方格纸上建立如图所示的平面直角坐标系,将△ABO绕点O按顺时针方向旋转90°,得△A′B′O.
(1)画出旋转后的图形;
(2)写出点A′,B′的坐标.
答案
一、单选题
1.D 2.A 3.A 4.D 5.A 6.B 7.A 8.C 9.C 10.C
二、填空题
11.旋转 12.30°或60°或150°或300° 13.36° 14.60 15.60 16.70°
三、解答题
17.解:(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示;
(3)旋转中心(﹣3,0).
故答案为:(﹣3,0).
18.解:在Rt△DOC,∠OCD=90°,OD=6,OC=3,
∴sin∠D=.
∴∠D=30°,
由旋转的性质可知:∠A=∠D=30°.
(2)在Rt△DOC,∠OCD=90°,∠D=30°,
∴∠DOC=60°,
∴∠AOD=180°﹣60°=120°,
∴线段OD扫过的面积为.
19.解:(1)如图所示:
A1的坐标是(3,﹣4);
(2)△A2B2C2是所求的三角形.
20.解:如图,
∵△ABC绕点B顺时针旋转60°后得到△DBE,
∴△ABC≌△DBE,
∴∠A=∠D,
又∵∠1=∠2,
∴∠DFA=∠ABD=60°,
∴∠EFC=∠DFA=60°
四、综合题
21.(1)解? :∵OA=AB=6,将△OAB绕点0沿逆时针方向旋转90°得到△OA1B1 ,
∴OA1=OA=6cm,
∵在Rt△OAB中,∠OAB=90°,OA=AB,
∴∠AOB=∠B=45°,
∵将△OAB绕点0沿逆时针方向旋转90°得到△OA1B1 ,
∴∠AOA1=90°,∠B1OA1=∠BOA=45°,
∴∠AOB1=90°+45°=135°,
(2)解 :∵将△OAB绕点0沿逆时针方向旋转90°得到△OA1B1,∠OAB=90°,OA=AB=6,
∴△AOB≌△A1OB1 ,
∴S四边形OAA1B1=2S△AOB=2××6×6=36cm2
22.(1)解:如图,△COD为所作;
(2)解:点A旋转过程中所经过的路程长= =2π≈6.3.
23.(1)解:①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图①:
∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC= ,AB=5,
∴BF=3,
∴BC=6,
∴B1C=BC=6,
∵CE⊥AB,
∴BE=B1E= ,
∴BB1= ,CE= ,
∴AB1= ,
∴△AB1C的面积为:
(2)解:如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1 , EF1有最小值,
此时在Rt△BFC中,CF= ,
∴CF1= ,
∴EF1的最小值为 ;
如图,以C为圆心BC为半径画圆交BC的延长线于F1 , EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为
24.(1)解:如图,△OA′B′即为旋转后的三角形
(2)解:由图可知,A′(2,3),B′(4,1).
(
1
)
同课章节目录
