3.3 垂径定理一课一练(含答案)
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第3节)
一、单选题(共10题;共20分)
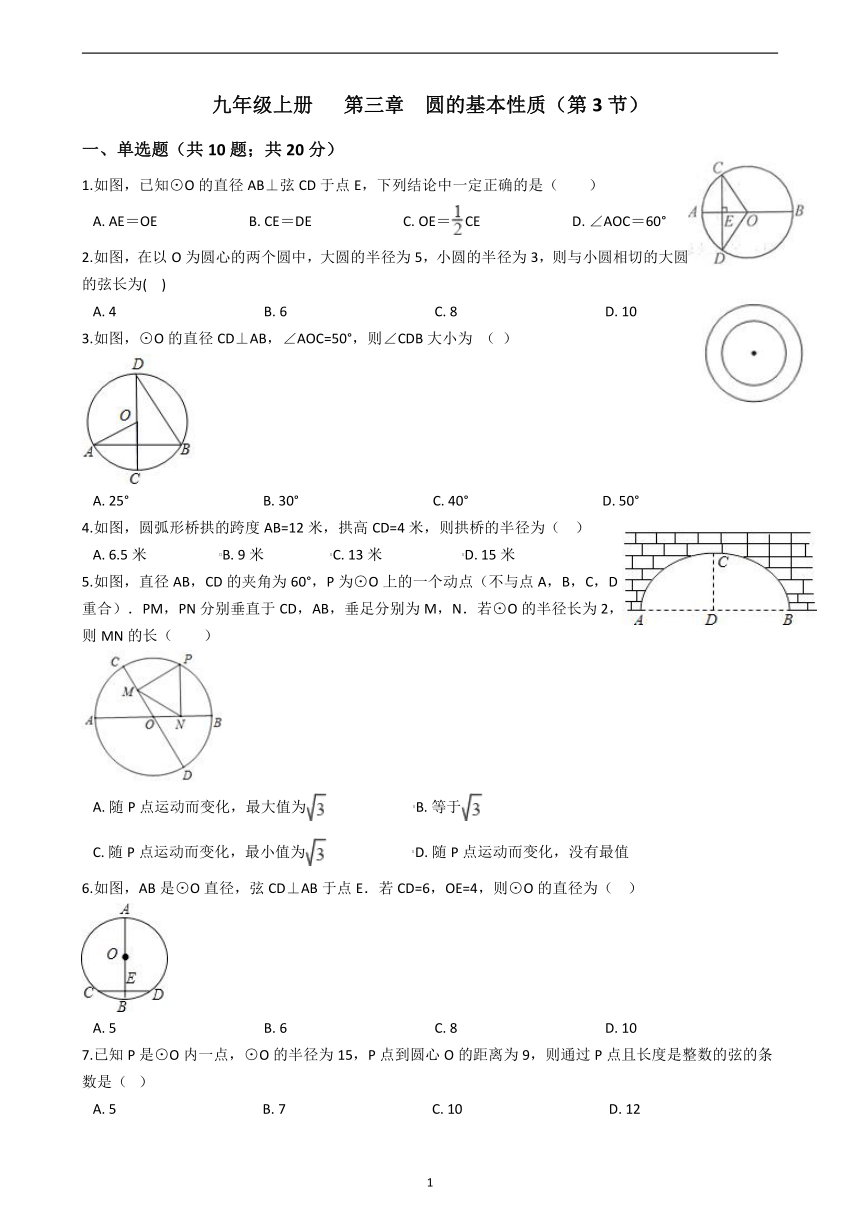
1.如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( ? ? )
A.?AE=OE??????????????????????????B.?CE=DE??????????????????????????C.?OE=CE??????????????????????????D.?∠AOC=60°
2.如图,在以O为圆心的两个圆中,大圆的半径为5,小圆的半径为3,则与小圆相切的大圆的弦长为(?? )???????
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
3.如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为 (??)
A.?25°???????????????????????????????????????B.?30°???????????????????????????????????????C.?40°???????????????????????????????????????D.?50°
4.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为(?? )
A.?6.5米?????????????????????B.?9米???????????????????C.?13米???????????????????????D.?15米
5.如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
A.?随P点运动而变化,最大值为?????????????????????????B.?等于
C.?随P点运动而变化,最小值为?????????????????????????D.?随P点运动而变化,没有最值
6.如图,AB是⊙O直径,弦CD⊥AB于点E.若CD=6,OE=4,则⊙O的直径为(?? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
7.已知P是⊙O内一点,⊙O的半径为15,P点到圆心O的距离为9,则通过P点且长度是整数的弦的条数是(? )
A.?5??????????????????????????????????????????B.?7??????????????????????????????????????????C.?10??????????????????????????????????????????D.?12
8.如图,AB为圆O的直径,C、D两点均在圆上,其中OD与AC交于E点,且OD⊥AC.若OE=4,ED=2,则BC长度为( )
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为(?? ?? )
A.?10???????????????????????????????????????????B.?8???????????????????????????????????????????C.?5???????????????????????????????????????????D.?3
10.如图,已知⊙O的半径为5,弦AB长度为8,则⊙O上到弦AB所在直线的距离为2的点有(?? )个.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题(共6题;共6分)
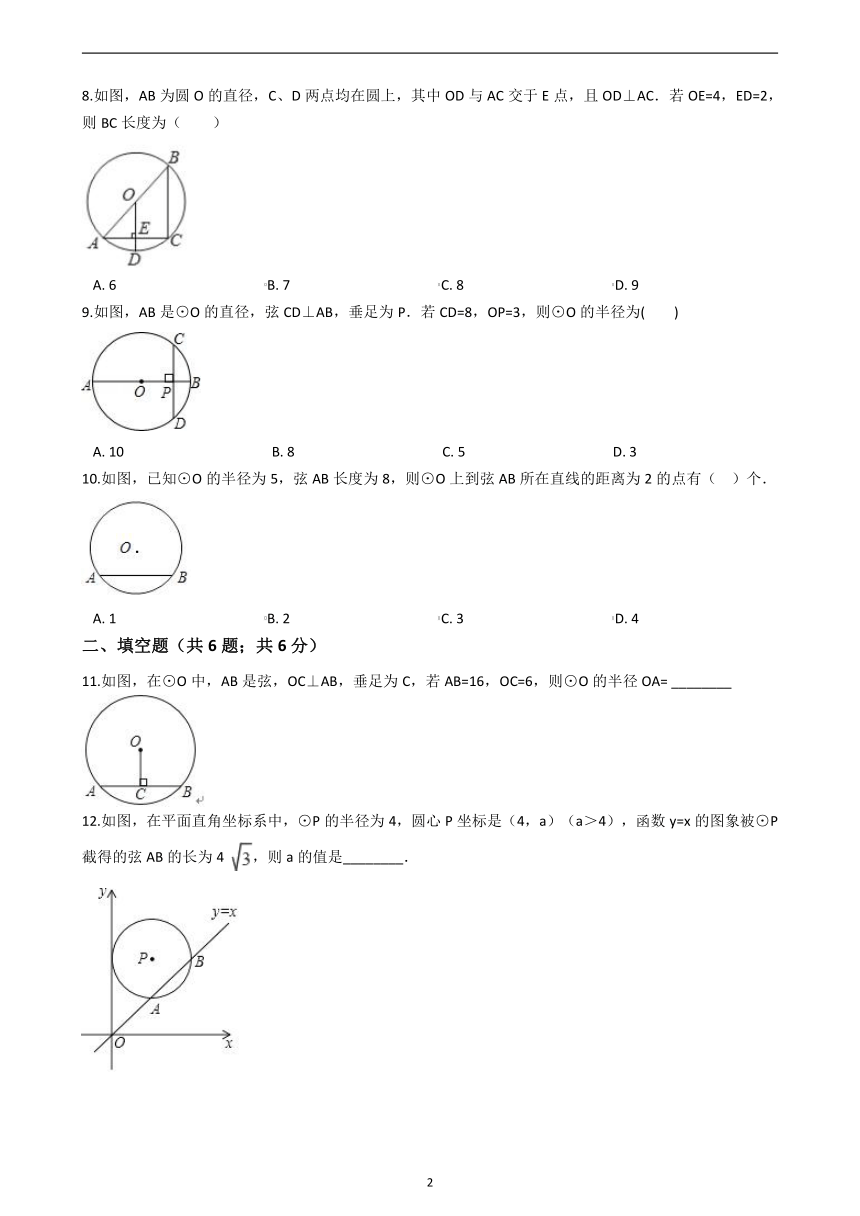
11.如图,在⊙O中,AB是弦,OC⊥AB,垂足为C,若AB=16,OC=6,则⊙O的半径OA=?________
12.如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4 ,则a的值是________.
13.为测量一铁球的直径,将该铁球放入工件槽内,测得有关数据如图所示(单位:cm),则该铁球的直径为________.
14.已知AB是⊙O的弦,如果⊙O的半径长为5,AB长为4,那么圆心O到弦AB的距离是?________
15.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=48cm,脸盆的最低点C到AB的距离为12 cm,则该脸盆的半径为________cm.
16.蔬菜基地建圆弧形蔬菜大棚的剖面如右图所示,已知AB=16m,半径 OA=10m,高度CD为________?m.
三、解答题(共4题;共20分)
17.已知:如图,已知点A、B、C在⊙O上,且点B是的中点,当OA=5cm,cos∠OAB=时.
(1)求△OAB的面积;
(2)联结AC,求弦AC的长.
18.如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?( =1.414)
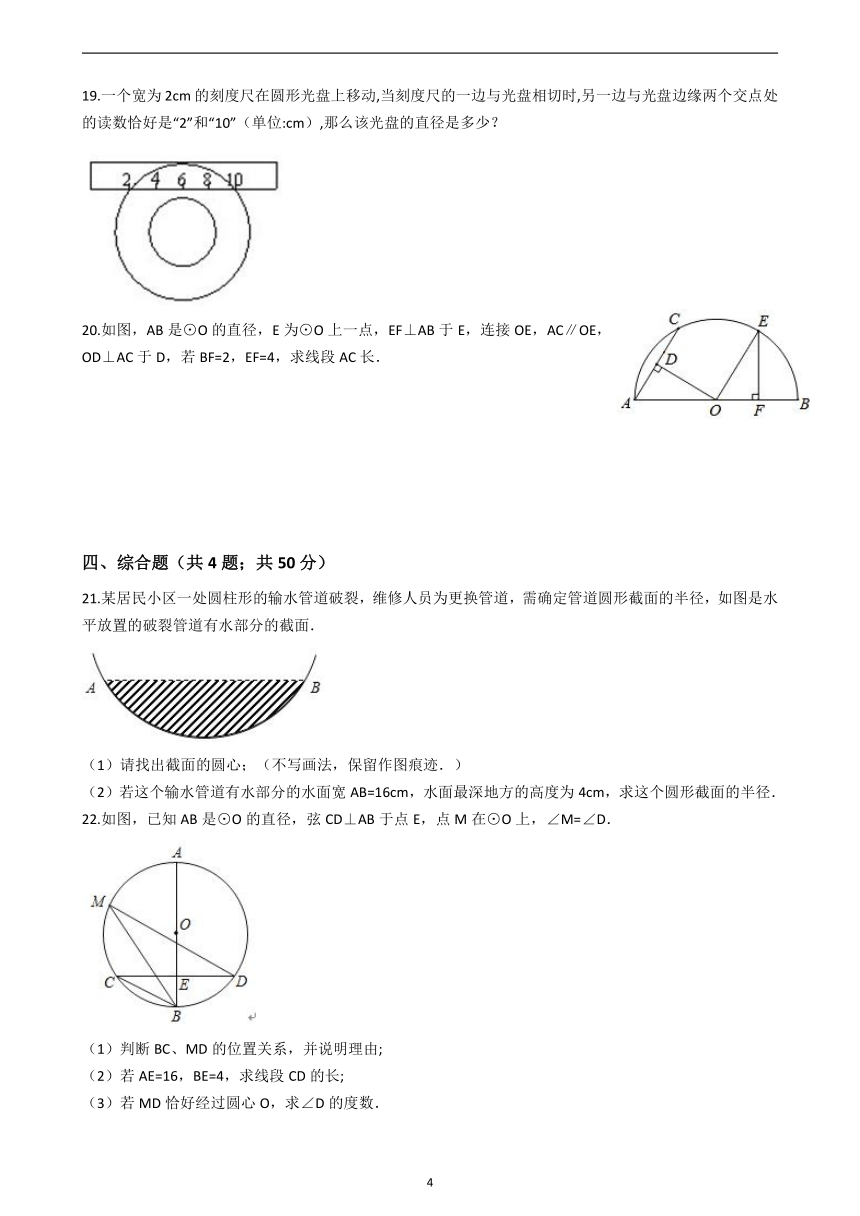
19.一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是多少?
20.如图,AB是⊙O的直径,E为⊙O上一点,EF⊥AB于E,连接OE,AC∥OE,OD⊥AC于D,若BF=2,EF=4,求线段AC长.
四、综合题(共4题;共50分)
21.某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请找出截面的圆心;(不写画法,保留作图痕迹.)
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
22.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
(1)判断BC、MD的位置关系,并说明理由;
(2)若AE=16,BE=4,求线段CD的长;
(3)若MD恰好经过圆心O,求∠D的度数.
23.如图,两个以点O为圆心的同心圆,
图1????????? 图2
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.
24.如图,已知:在⊙O中,弦AB为8,圆心O到AB的距离为3.
(1)求圆的半径;
(2)若点P是AB上的一动点,试求OP最大值和最小值.
答案
一、单选题
1.B 2.C 3.A 4.A 5.B 6.D 7.D 8.C 9.C 10.C
二、填空题
11.10 12.4+2 13.10cm 14.15.30 16.4
三、解答题
17.解:(1)过O作OH⊥AB于H,
∵cos∠OAB=,
∴=,
∴AH=3cm,OH=4cm,AB=2AH=6cm,
∴S△OAB=AB?OH=12cm2;
(2)设AC交OB于M,∵B是的中点,
∴,∴AB=BC,
∵OA=OC,
故O,B均在线段AC的垂直平分线上,
∴OB垂直平分AC,
∴AM=AB?sin∠MBA=6×,
∴AC=2AM=cm.
18.解:
设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP′,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2 ,
即x2=(x﹣18)2+302 , 解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N= = =16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施
19.解:如图,设圆心为O,弦为AB,切点为C.如图所示.则AB=8cm,CD=2cm.
连接OC,交AB于D点.连接OA.
∵尺的对边平行,光盘与外边缘相切,
∴OC⊥AB.
∴AD=4cm.
设半径为Rcm,则R2=42+(R﹣2)2,
解得R=5,
∴该光盘的直径是10cm.
20.解:设OE=x,则OF=x﹣2, 由勾股定理得,OE2=OF2+EF2 , 即x2=(x﹣2)2+42 ,
解得,x=5,
∴OF=3,
∵AC∥OE,OD⊥AC,
∴OD⊥OE,
∵OA=OE,EF⊥AB,
∴△ADO≌△OFE,
∴AD=OF=3,
∵OD⊥AC,
∴AC=2AD=6.
四、综合题
21.(1)解:如图所示
(2)解:如图,OE⊥AB交AB于点D,
则DE=4cm,AB=16cm,AD=8cm,
设半径为Rcm,则
OD=OE﹣DE=R﹣4,
由勾股定理得,OA2=AD2+OD2 ,
即R2=82+(R﹣4)2 ,
解得R=10.
故这个圆形截面的半径是10cm
22.(1)解:
BC∥MD.
理由:∵∠M=∠D,∠M=∠C,∠D=∠CBM,
∴∠M=∠D=∠C=∠CBM,
∴BC∥MD.
(2)解:
∵AE=16,BE=4,
∴OB==10,
∴OE=10﹣4=6,
连接OC,
∵CD⊥AB,
∴CE=CD,
在Rt△OCE中,
∵OE2+CE2=OC2 , 即62+CE2=102 , 解得CE=8,
∴CD=2CE=16.
?
(3)解:
如图2,
∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=×90°=30°.
?
23.(1)解:AC=BD,理由是:过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,
AH-CH=BH-DH,
即AC=BD
(2)解:连接OC,如图,
AB是小圆的切线,
OC⊥AB,则AC=BC
(3)解:如图,连接OB.
∵大圆的弦AB是小圆的切线,
∴OC⊥AB,AC=CB,
∴OB2-OC2=(20÷2)2=102 ,
∵S圆环=S大-S小=π?OB2-π?OC2=π?(OB2-OC2),
∴S圆环=100πcm2
24.(1)解:连接AO,过O作OD⊥AB,
∵弦AB为8,
∴AD=4,
∵圆心O到AB的距离为3,
∴DO=3,
∴AO= = =5,
∴圆的半径是5;
(2)解:∵点P是AB上的一动点, ∴OP最大值是5,OP最小值是3.
(
1
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第3节)
一、单选题(共10题;共20分)
1.如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( ? ? )
A.?AE=OE??????????????????????????B.?CE=DE??????????????????????????C.?OE=CE??????????????????????????D.?∠AOC=60°
2.如图,在以O为圆心的两个圆中,大圆的半径为5,小圆的半径为3,则与小圆相切的大圆的弦长为(?? )???????
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
3.如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为 (??)
A.?25°???????????????????????????????????????B.?30°???????????????????????????????????????C.?40°???????????????????????????????????????D.?50°
4.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为(?? )
A.?6.5米?????????????????????B.?9米???????????????????C.?13米???????????????????????D.?15米
5.如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
A.?随P点运动而变化,最大值为?????????????????????????B.?等于
C.?随P点运动而变化,最小值为?????????????????????????D.?随P点运动而变化,没有最值
6.如图,AB是⊙O直径,弦CD⊥AB于点E.若CD=6,OE=4,则⊙O的直径为(?? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
7.已知P是⊙O内一点,⊙O的半径为15,P点到圆心O的距离为9,则通过P点且长度是整数的弦的条数是(? )
A.?5??????????????????????????????????????????B.?7??????????????????????????????????????????C.?10??????????????????????????????????????????D.?12
8.如图,AB为圆O的直径,C、D两点均在圆上,其中OD与AC交于E点,且OD⊥AC.若OE=4,ED=2,则BC长度为( )
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为(?? ?? )
A.?10???????????????????????????????????????????B.?8???????????????????????????????????????????C.?5???????????????????????????????????????????D.?3
10.如图,已知⊙O的半径为5,弦AB长度为8,则⊙O上到弦AB所在直线的距离为2的点有(?? )个.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题(共6题;共6分)
11.如图,在⊙O中,AB是弦,OC⊥AB,垂足为C,若AB=16,OC=6,则⊙O的半径OA=?________
12.如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4 ,则a的值是________.
13.为测量一铁球的直径,将该铁球放入工件槽内,测得有关数据如图所示(单位:cm),则该铁球的直径为________.
14.已知AB是⊙O的弦,如果⊙O的半径长为5,AB长为4,那么圆心O到弦AB的距离是?________
15.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=48cm,脸盆的最低点C到AB的距离为12 cm,则该脸盆的半径为________cm.
16.蔬菜基地建圆弧形蔬菜大棚的剖面如右图所示,已知AB=16m,半径 OA=10m,高度CD为________?m.
三、解答题(共4题;共20分)
17.已知:如图,已知点A、B、C在⊙O上,且点B是的中点,当OA=5cm,cos∠OAB=时.
(1)求△OAB的面积;
(2)联结AC,求弦AC的长.
18.如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?( =1.414)
19.一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是多少?
20.如图,AB是⊙O的直径,E为⊙O上一点,EF⊥AB于E,连接OE,AC∥OE,OD⊥AC于D,若BF=2,EF=4,求线段AC长.
四、综合题(共4题;共50分)
21.某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请找出截面的圆心;(不写画法,保留作图痕迹.)
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
22.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
(1)判断BC、MD的位置关系,并说明理由;
(2)若AE=16,BE=4,求线段CD的长;
(3)若MD恰好经过圆心O,求∠D的度数.
23.如图,两个以点O为圆心的同心圆,
图1????????? 图2
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.
24.如图,已知:在⊙O中,弦AB为8,圆心O到AB的距离为3.
(1)求圆的半径;
(2)若点P是AB上的一动点,试求OP最大值和最小值.
答案
一、单选题
1.B 2.C 3.A 4.A 5.B 6.D 7.D 8.C 9.C 10.C
二、填空题
11.10 12.4+2 13.10cm 14.15.30 16.4
三、解答题
17.解:(1)过O作OH⊥AB于H,
∵cos∠OAB=,
∴=,
∴AH=3cm,OH=4cm,AB=2AH=6cm,
∴S△OAB=AB?OH=12cm2;
(2)设AC交OB于M,∵B是的中点,
∴,∴AB=BC,
∵OA=OC,
故O,B均在线段AC的垂直平分线上,
∴OB垂直平分AC,
∴AM=AB?sin∠MBA=6×,
∴AC=2AM=cm.
18.解:
设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP′,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2 ,
即x2=(x﹣18)2+302 , 解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N= = =16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施
19.解:如图,设圆心为O,弦为AB,切点为C.如图所示.则AB=8cm,CD=2cm.
连接OC,交AB于D点.连接OA.
∵尺的对边平行,光盘与外边缘相切,
∴OC⊥AB.
∴AD=4cm.
设半径为Rcm,则R2=42+(R﹣2)2,
解得R=5,
∴该光盘的直径是10cm.
20.解:设OE=x,则OF=x﹣2, 由勾股定理得,OE2=OF2+EF2 , 即x2=(x﹣2)2+42 ,
解得,x=5,
∴OF=3,
∵AC∥OE,OD⊥AC,
∴OD⊥OE,
∵OA=OE,EF⊥AB,
∴△ADO≌△OFE,
∴AD=OF=3,
∵OD⊥AC,
∴AC=2AD=6.
四、综合题
21.(1)解:如图所示
(2)解:如图,OE⊥AB交AB于点D,
则DE=4cm,AB=16cm,AD=8cm,
设半径为Rcm,则
OD=OE﹣DE=R﹣4,
由勾股定理得,OA2=AD2+OD2 ,
即R2=82+(R﹣4)2 ,
解得R=10.
故这个圆形截面的半径是10cm
22.(1)解:
BC∥MD.
理由:∵∠M=∠D,∠M=∠C,∠D=∠CBM,
∴∠M=∠D=∠C=∠CBM,
∴BC∥MD.
(2)解:
∵AE=16,BE=4,
∴OB==10,
∴OE=10﹣4=6,
连接OC,
∵CD⊥AB,
∴CE=CD,
在Rt△OCE中,
∵OE2+CE2=OC2 , 即62+CE2=102 , 解得CE=8,
∴CD=2CE=16.
?
(3)解:
如图2,
∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=×90°=30°.
?
23.(1)解:AC=BD,理由是:过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,
AH-CH=BH-DH,
即AC=BD
(2)解:连接OC,如图,
AB是小圆的切线,
OC⊥AB,则AC=BC
(3)解:如图,连接OB.
∵大圆的弦AB是小圆的切线,
∴OC⊥AB,AC=CB,
∴OB2-OC2=(20÷2)2=102 ,
∵S圆环=S大-S小=π?OB2-π?OC2=π?(OB2-OC2),
∴S圆环=100πcm2
24.(1)解:连接AO,过O作OD⊥AB,
∵弦AB为8,
∴AD=4,
∵圆心O到AB的距离为3,
∴DO=3,
∴AO= = =5,
∴圆的半径是5;
(2)解:∵点P是AB上的一动点, ∴OP最大值是5,OP最小值是3.
(
1
)
同课章节目录
