浙教版初中数学九年级上册3.6 圆内接四边形同步练习含答案
文档属性
| 名称 | 浙教版初中数学九年级上册3.6 圆内接四边形同步练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 180.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-13 19:14:45 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第6节)
一、单选题(共10题;共20分)
1.下列说法错误的是( )
A.?圆内接四边形的对角互补????????????????????????????????????B.?圆内接四边形的邻角互补
C.?圆内接平行四边形是矩形????????????????????????????????????D.?圆内接梯形是等腰梯形
2.如图,四边形ABCD是⊙O的内接四边形,若∠B=80°,则∠ADC的度数是(??? )
A.?60°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
3.如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )
A.?55°???????????????????????????????????????B.?45°???????????????????????????????????????C.?35°???????????????????????????????????????D.?25°
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是(?? )
A.?115°?????????????????????????????????????B.?105°?????????????????????????????????????C.?100°?????????????????????????????????????D.?95°
5.边长为1的正六边形的内切圆的半径为( )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.????????????????????????????????????????????D.?
6.如图,四边形ABCD是圆内接四边形,若∠BAD =105°,则∠BCD的度数是( ??)
A.?105°??????????????????????????????????????B.?95°??????????????????????????????????????C.?75°??????????????????????????????????????D.?60°
7.如图,四边形ABCD是⊙O的内接四边形,∠ABC=100°,则∠ADC=( )
A.?70°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
8.若同一个圆的内接正三角形、正方形、正六边形的边长分别记作a3 , a4 , a6 , 则a3:a4:a6等于( )
A.?1::?????????????????????????B.?1:2:3?????????????????????????C.?3:2:1?????????????????????????D.?::1
9.有一个边长为50cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为( )
A.?50cm????????????????????????????B.?25cm????????????????????????????C.?50cm?????????????????????????????D.?50cm
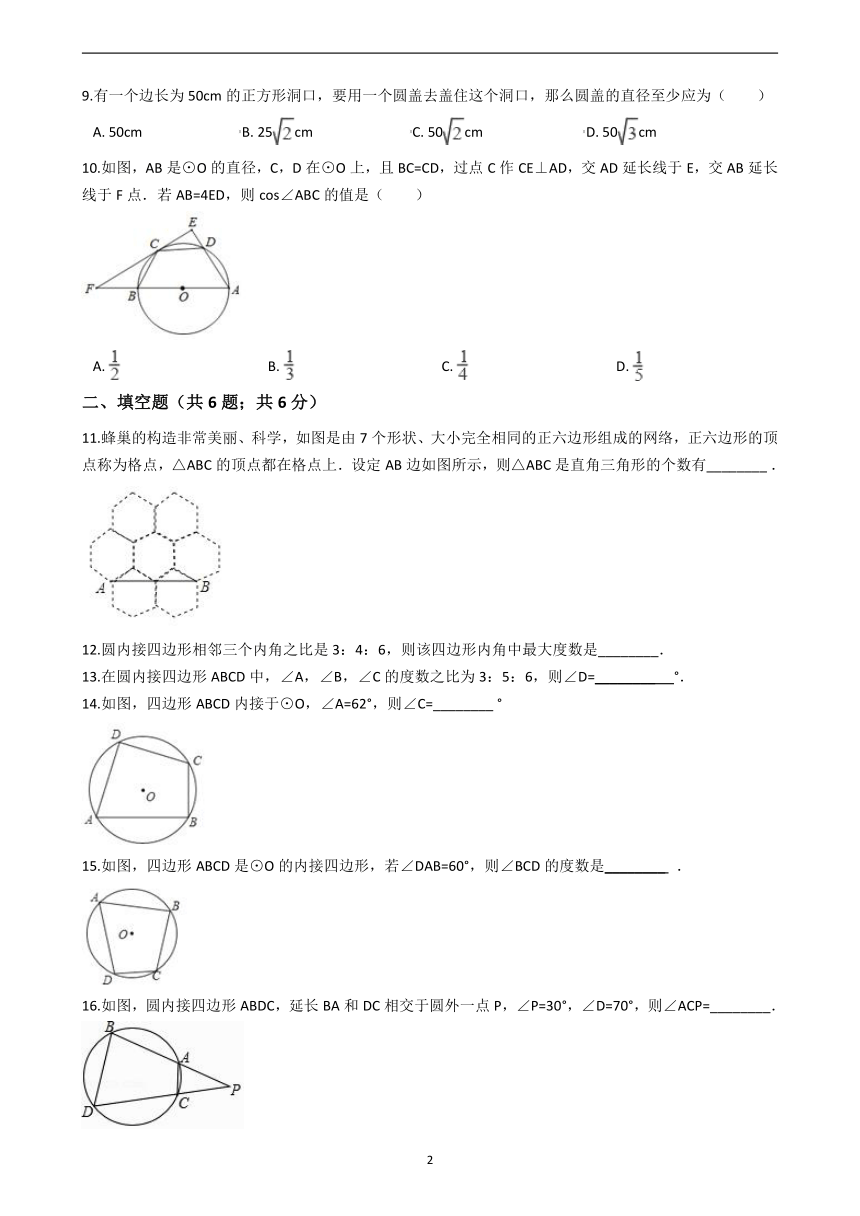
10.如图,AB是⊙O的直径,C,D在⊙O上,且BC=CD,过点C作CE⊥AD,交AD延长线于E,交AB延长线于F点.若AB=4ED,则cos∠ABC的值是( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题(共6题;共6分)
11.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有________?.
12.圆内接四边形相邻三个内角之比是3:4:6,则该四边形内角中最大度数是________.
13.在圆内接四边形ABCD中,∠A,∠B,∠C的度数之比为3:5:6,则∠D=________? °.
14.如图,四边形ABCD内接于⊙O,∠A=62°,则∠C=________?°
15.如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是________? .
16.如图,圆内接四边形ABDC,延长BA和DC相交于圆外一点P,∠P=30°,∠D=70°,则∠ACP=________.
三、解答题(共5题;共25分)
17.如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
18.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.
(1)若∠E+∠F=α,求∠A的度数(用含α的式子表示);
(2)若∠E+∠F=60°,求∠A的度数.
19.在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在上,求∠E的度数.
20.已知圆内接正三角形的边心距为2cm,求它的边长.
21.如图,圆内接四边形ABCD的两组对边延长线分别交于E、F,∠AEB、∠AFD的平分线交于P点.求证:PE⊥PF.
四、综合题(共1题;共10分)
22.????? 综合题:
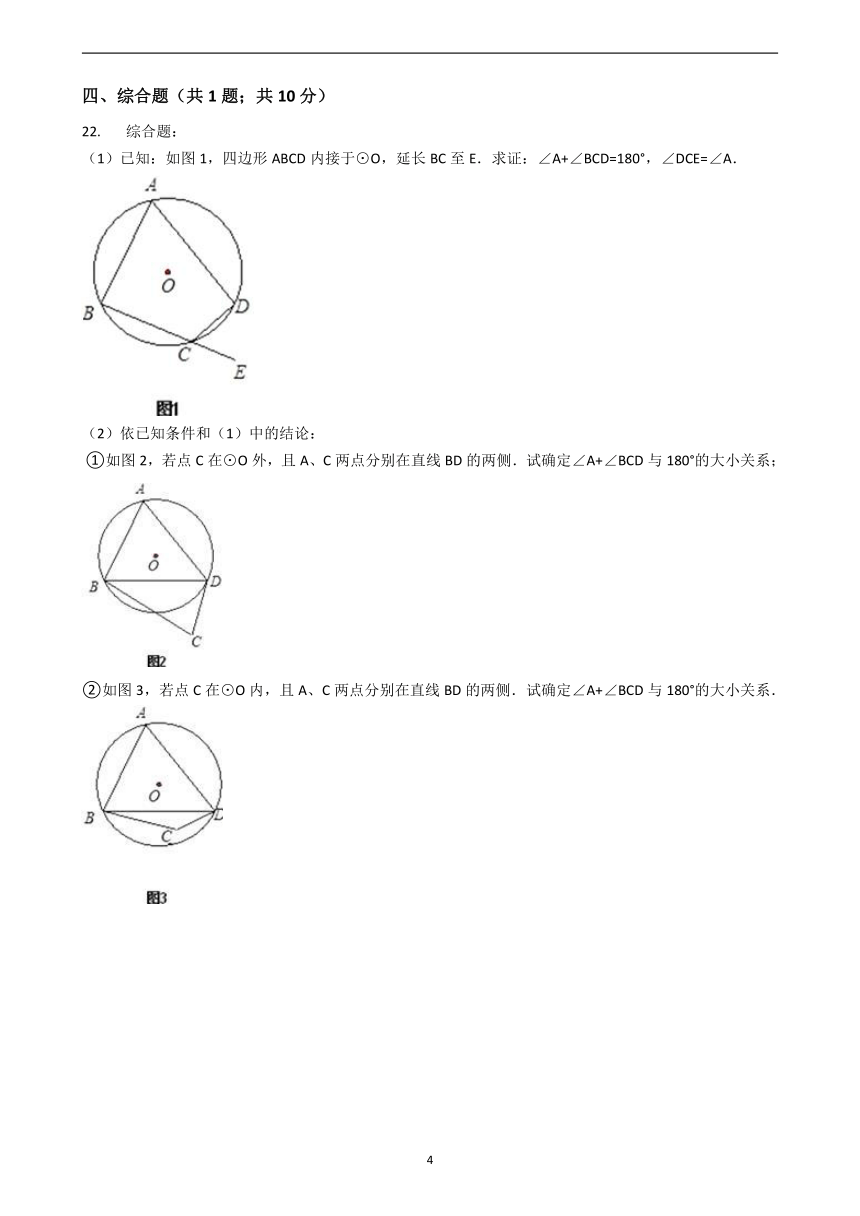
(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
?①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
答案
一、单选题
1.B 2.D 3.D 4.B 5.D 6.C 7.B 8.D 9.C 10.A
二、填空题
11.10 12.120° 13.80 14.118 15.120° 16.80°
三、解答题
17.证明:∵A、D、C、B四点共圆,
∴∠A=∠BCE,
∵BC=BE,
∴∠BCE=∠E,
∴∠A=∠E,
∴AD=DE,
即△ADE是等腰三角形.
18.解:(1)∵四边形ABCD为⊙O的内接四边形,
∴∠A=∠BCF,
∵∠EBF=∠A+∠E,
而∠EBF=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180﹣∠A﹣∠F,
即2∠A=180°﹣(∠E+∠F),
∵∠E+∠F=α,
∴∠A=90°﹣α;
(2)当α=60°时,∠A=90°﹣×60°=60°.
19.解:连接BD,
∵∠C+∠BAD=180°,
∴∠BAD=180°﹣110°=70°,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ABD=(180°﹣70°)=55°,
∵四边形ABDE为圆的内接四边形,
∴∠E+∠ABD=180°,
∴∠E=180°﹣55°=125°.
20.解:如图,连接OA、OB;
∵AB为⊙O的内接正三角形的一边,OC⊥AB于点C;
∴∠AOB==120°;
∵OA=OB,
∴∠AOC=∠AOB=60°,AC=BC;
∵tan60°= ,而OC=2,
∴AC=2,AB=4(cm).
21.证明:∵四边形ABCD内接于圆,
∴∠BCF=∠A,
∵FM平分∠BFC,
∴∠BFN=∠CFN,
∵∠EMP=∠A+∠BFN,∠PNE=∠BCF+∠CFN,
∴∠EMP=∠PNE,
∴EM=EN,
∵PE平分∠MEN,
∴PE⊥PF.
四、综合题
22.(1)证明:连结AC,BD,
∴∠CAD=∠CBD,∠ABD=∠ACD,∠ADB=∠ACB,∠BAC=∠BDC,
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠CAD+∠BAC+∠ABD+∠CBD+∠ACB+∠ACD+∠ADB+∠BDC=360°,
∴∠CAD+∠BAC+∠ACB+∠ACD=180°,
即∠BAD+∠BCD=180°,
又∵∠DCE+∠BCD=180°,
∴∠BAD=∠DCE.
(2)解:①设BC与⊙O交于点E,连结DE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BED=∠CDE+∠BCD,
∴∠BED>∠BCD,
∴∠A+∠BCD<180°.
②延长DC交⊙O于点E,连结BE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BCD=∠CBE+∠BED,
∴∠BCD>∠BED,
∴∠A+∠BCD>180°.
(
1
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第6节)
一、单选题(共10题;共20分)
1.下列说法错误的是( )
A.?圆内接四边形的对角互补????????????????????????????????????B.?圆内接四边形的邻角互补
C.?圆内接平行四边形是矩形????????????????????????????????????D.?圆内接梯形是等腰梯形
2.如图,四边形ABCD是⊙O的内接四边形,若∠B=80°,则∠ADC的度数是(??? )
A.?60°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
3.如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )
A.?55°???????????????????????????????????????B.?45°???????????????????????????????????????C.?35°???????????????????????????????????????D.?25°
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是(?? )
A.?115°?????????????????????????????????????B.?105°?????????????????????????????????????C.?100°?????????????????????????????????????D.?95°
5.边长为1的正六边形的内切圆的半径为( )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.????????????????????????????????????????????D.?
6.如图,四边形ABCD是圆内接四边形,若∠BAD =105°,则∠BCD的度数是( ??)
A.?105°??????????????????????????????????????B.?95°??????????????????????????????????????C.?75°??????????????????????????????????????D.?60°
7.如图,四边形ABCD是⊙O的内接四边形,∠ABC=100°,则∠ADC=( )
A.?70°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
8.若同一个圆的内接正三角形、正方形、正六边形的边长分别记作a3 , a4 , a6 , 则a3:a4:a6等于( )
A.?1::?????????????????????????B.?1:2:3?????????????????????????C.?3:2:1?????????????????????????D.?::1
9.有一个边长为50cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为( )
A.?50cm????????????????????????????B.?25cm????????????????????????????C.?50cm?????????????????????????????D.?50cm
10.如图,AB是⊙O的直径,C,D在⊙O上,且BC=CD,过点C作CE⊥AD,交AD延长线于E,交AB延长线于F点.若AB=4ED,则cos∠ABC的值是( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题(共6题;共6分)
11.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有________?.
12.圆内接四边形相邻三个内角之比是3:4:6,则该四边形内角中最大度数是________.
13.在圆内接四边形ABCD中,∠A,∠B,∠C的度数之比为3:5:6,则∠D=________? °.
14.如图,四边形ABCD内接于⊙O,∠A=62°,则∠C=________?°
15.如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是________? .
16.如图,圆内接四边形ABDC,延长BA和DC相交于圆外一点P,∠P=30°,∠D=70°,则∠ACP=________.
三、解答题(共5题;共25分)
17.如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
18.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.
(1)若∠E+∠F=α,求∠A的度数(用含α的式子表示);
(2)若∠E+∠F=60°,求∠A的度数.
19.在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在上,求∠E的度数.
20.已知圆内接正三角形的边心距为2cm,求它的边长.
21.如图,圆内接四边形ABCD的两组对边延长线分别交于E、F,∠AEB、∠AFD的平分线交于P点.求证:PE⊥PF.
四、综合题(共1题;共10分)
22.????? 综合题:
(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
?①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
答案
一、单选题
1.B 2.D 3.D 4.B 5.D 6.C 7.B 8.D 9.C 10.A
二、填空题
11.10 12.120° 13.80 14.118 15.120° 16.80°
三、解答题
17.证明:∵A、D、C、B四点共圆,
∴∠A=∠BCE,
∵BC=BE,
∴∠BCE=∠E,
∴∠A=∠E,
∴AD=DE,
即△ADE是等腰三角形.
18.解:(1)∵四边形ABCD为⊙O的内接四边形,
∴∠A=∠BCF,
∵∠EBF=∠A+∠E,
而∠EBF=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180﹣∠A﹣∠F,
即2∠A=180°﹣(∠E+∠F),
∵∠E+∠F=α,
∴∠A=90°﹣α;
(2)当α=60°时,∠A=90°﹣×60°=60°.
19.解:连接BD,
∵∠C+∠BAD=180°,
∴∠BAD=180°﹣110°=70°,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ABD=(180°﹣70°)=55°,
∵四边形ABDE为圆的内接四边形,
∴∠E+∠ABD=180°,
∴∠E=180°﹣55°=125°.
20.解:如图,连接OA、OB;
∵AB为⊙O的内接正三角形的一边,OC⊥AB于点C;
∴∠AOB==120°;
∵OA=OB,
∴∠AOC=∠AOB=60°,AC=BC;
∵tan60°= ,而OC=2,
∴AC=2,AB=4(cm).
21.证明:∵四边形ABCD内接于圆,
∴∠BCF=∠A,
∵FM平分∠BFC,
∴∠BFN=∠CFN,
∵∠EMP=∠A+∠BFN,∠PNE=∠BCF+∠CFN,
∴∠EMP=∠PNE,
∴EM=EN,
∵PE平分∠MEN,
∴PE⊥PF.
四、综合题
22.(1)证明:连结AC,BD,
∴∠CAD=∠CBD,∠ABD=∠ACD,∠ADB=∠ACB,∠BAC=∠BDC,
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠CAD+∠BAC+∠ABD+∠CBD+∠ACB+∠ACD+∠ADB+∠BDC=360°,
∴∠CAD+∠BAC+∠ACB+∠ACD=180°,
即∠BAD+∠BCD=180°,
又∵∠DCE+∠BCD=180°,
∴∠BAD=∠DCE.
(2)解:①设BC与⊙O交于点E,连结DE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BED=∠CDE+∠BCD,
∴∠BED>∠BCD,
∴∠A+∠BCD<180°.
②延长DC交⊙O于点E,连结BE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BCD=∠CBE+∠BED,
∴∠BCD>∠BED,
∴∠A+∠BCD>180°.
(
1
)
同课章节目录
