3.7 正多边形一课一练(含答案)
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第7节)
一、单选题(共10题;共20分)
1.正六边形的边心距与边长之比为(??? )
A.?1 : 2?????????????????????????????????B.?:2?????????????????????????????????C.?:1?????????????????????????????????D.?:2
2.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为(?? )cm.
A.?2 ?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?4
3.若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
A.?????????????????????????????????????????B.??????????????????????????????????????????C.????????????????????????????????????????D.?π
4.正五边形的中心角等于( )
A.?18°???????????????????????????????????????B.?36°???????????????????????????????????????C.?54°???????????????????????????????????????D.?72°
5.半径为a的正六边形的面积等于( )
A.???????????????????????????????????B.???????????????????????????????????C.?a2?????????????????????????????????????D.?
6.等边三角形的内切圆半径,外接圆半径和高的比是(??? )
A.?????????????????????????????B.?2:3:4????????????????????????????C.?????????????????????????????D.?1:2:3
7.已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
A.?32﹣32﹣4π???????????????????????????????B.????????????????????????????????C.?1???????????????????????????????D.?16﹣4π
8.如果圆形纸片的直径是8cm,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
A.?2cm?????????????????????????????????B.?2cm??????????????????????????????????C.?4cm?????????????????????????????????D.?4Cm
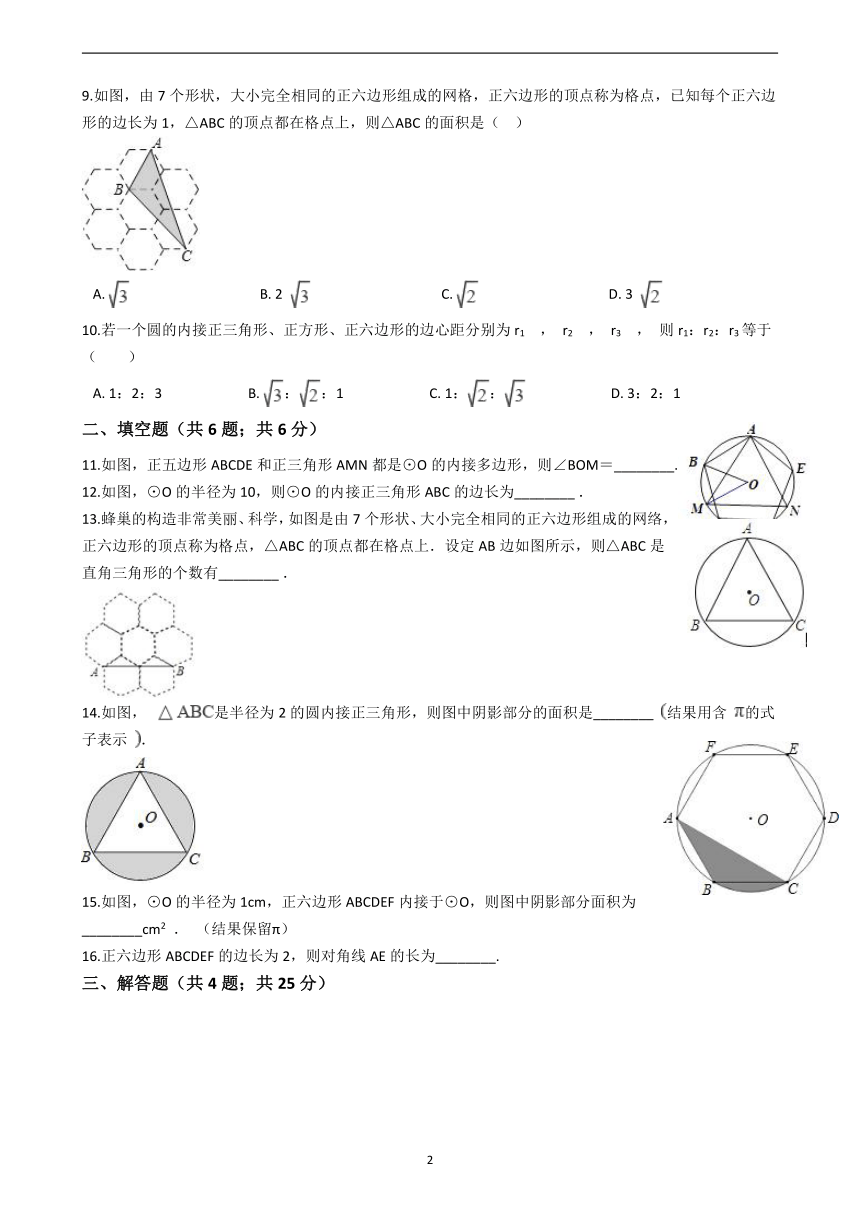
9.如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是(?? )
A.???????????????????????????????????????B.?2 ??????????????????????????????????????C.???????????????????????????????????????D.?3
10.若一个圆的内接正三角形、正方形、正六边形的边心距分别为r1 , r2 , r3 , 则r1:r2:r3等于( )
A.?1:2:3?????????????????????????B.?::1?????????????????????????C.?1::?????????????????????????D.?3:2:1
二、填空题(共6题;共6分)
11.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=________.
12.如图,⊙O的半径为10,则⊙O的内接正三角形ABC的边长为________?.
13.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有________?.
14.如图, 是半径为2的圆内接正三角形,则图中阴影部分的面积是________ 结果用含 的式子表示 .
15.如图,⊙O的半径为1cm,正六边形ABCDEF内接于⊙O,则图中阴影部分面积为________cm2 . (结果保留π)
16.正六边形ABCDEF的边长为2,则对角线AE的长为________.
三、解答题(共4题;共25分)
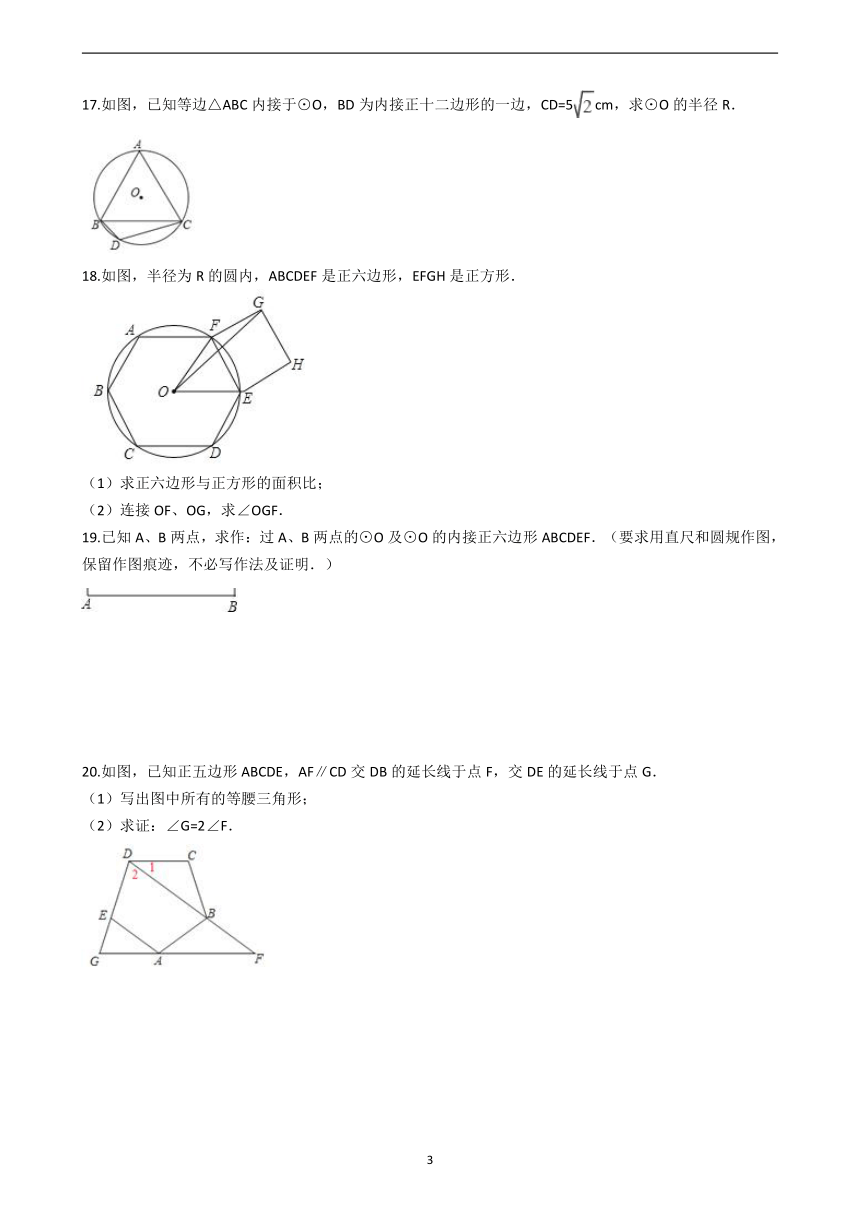
17.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
18.如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;
(2)连接OF、OG,求∠OGF.
19.已知A、B两点,求作:过A、B两点的⊙O及⊙O的内接正六边形ABCDEF.(要求用直尺和圆规作图,保留作图痕迹,不必写作法及证明.)
20.如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
四、综合题(共4题;共47分)
21.如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
(1)求这个正六边形的边长.
(2)求这个正六边形的边心距.
(3)根据题意画出图形,根据圆的面积公式计算即可.
22.如图,已知正五边形AB CDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
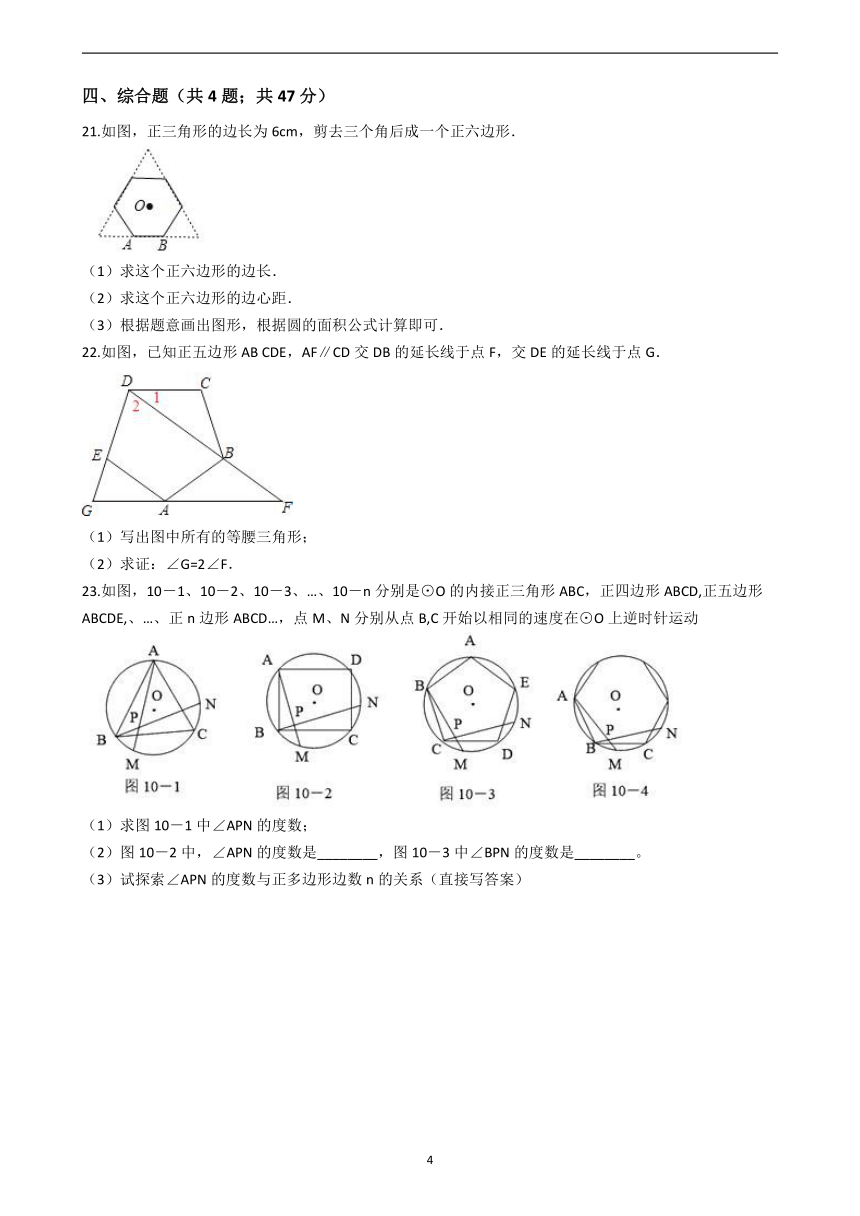
23.如图,10-1、10-2、10-3、…、10-n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动
(1)求图10-1中∠APN的度数;
(2)图10-2中,∠APN的度数是________,图10-3中∠BPN的度数是________。
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
24.如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
答案
一、单选题
1.D 2.B 3.A 4.D 5.B 6.D 7.A 8.C 9.B 10.C
二、填空题
11.48° 12.10 13.10 14.15.16.?
三、解答题
17.解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD?cos45°=5×=5(cm).
即⊙O的半径R=5cm.
18.(1)解:设正六边形的边长为a,
则三角形OEF的边EF上的高为a,
则正六边形的面积为:6××a×a=a2 ,
∴正方形的面积为:a×a=a2 ,
∴正六边形与正方形的面积比a2:a2=3:2;
(2)解:∵OF=EF=FG,
∴∠OGF=(180°﹣60°﹣90°)=15°.
19.答:如图所示:
首先以AB为直径作圆,在以AB的一半为半径在圆上截取相等的弧,然后顺次连接六个等分点即可.
?
20.(1)解:∵DC=BC,
∴△CDB是等腰三角形,
∵∠C=108°,
∴∠1=∠CBD=36°,
∵AF∥CD,
∴∠F=∠1=36°,
可得四边形DEAB是等腰梯形,
∴∠DBA=∠2=72°,
∴∠F=∠BAF=36°,
∴△BAF是等腰三角形,
进而可得:∠GEA=∠G=∠2=72°,
∴△FDG,△AEG是等腰三角形,
故等腰三角形有:△BCD,△ABF,△FDG,△AEG.
(2)证明:∵五边形ABCDE是正五边形,
∴∠C=∠CDE=108°,CD=CB.
得∠1=36°,
∴∠2=108°﹣36°=72°.
又∵AF∥CD,
∴∠F=∠1=36°,
故∠G=180°﹣∠2﹣∠F=180°﹣72°﹣36°=72°=2∠F.
四、综合题
21.(1)解:∵正三角形的边长为6cm,
∴3个边长都相等,
又∵截去三个小等边三角形,
∴各个小三角形的边长也相等,
∴正六边形的边长为:2;
(2)解:连接OA,OB,过点O作OD⊥AB于点D,
∵∠AOB==60°,
∴△OAB是等边三角形,
∴OD=OA?sin60°=2×=;
(3)解:如图2:
线段AB划过的面积=π×22﹣π×()2=πcm2 .
22.(1)解:∵正五边形ABCDE
∴DC=BC,∠C=108°
∴△CDB是等腰三角形,
∴∠1=∠CBD=36°,
∵AF∥CD,
∴∠F=∠1=36°,
可得四边形DEAB是等腰梯形,
∴∠DBA=∠2=72°,
∴∠F=∠BAF=36°,
∴△BAF是等腰三角形,
同理可得:∠GEA=∠G=∠2=72°,
∴△FDG,△AEG是等腰三角形,
故等腰三角形有:△BCD,△ABF,△FDG,△AEG.
(2)证明:证明:∵五边形ABCDE是正五边形,
∴∠C=∠CDE=108°,CD=CB.
得∠1=36°,
∴∠2=108°?36°=72°.
又∵AF∥CD,
∴∠F=∠1=36°,
∴∠G=180°?∠2?∠F=180°?72°?36°=72°=2∠F,
23.(1)图1:∵点M、N分别从点B. C开始以相同的速度在O上逆时针运动,
∴劣弧BM=劣弧CN
∴∠BAM=∠CBN,
∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°。
(2)90°;108°
(3)由(1)、(2)可知,∠APN=它所在的正多边形的内角度数。
24.(1)证明:(1)连接OD.
∵四边形ABCD为正方形,AE=AB.
∴AE=AB=AD,∠EAD=∠DAB=90°,
∴∠EDA=45°,∠ODA=45°,
∴∠ODE=∠ADE+∠ODA=90°,
∴直线ED是⊙O的切线.
(2)证明:作OM⊥AB于M,
∵O为正方形的中心,
∴M为AB中点,
∴AE=AB=2AM,AF∥OM,
∴
∴EF=2FO.
(
1
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第7节)
一、单选题(共10题;共20分)
1.正六边形的边心距与边长之比为(??? )
A.?1 : 2?????????????????????????????????B.?:2?????????????????????????????????C.?:1?????????????????????????????????D.?:2
2.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为(?? )cm.
A.?2 ?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?4
3.若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
A.?????????????????????????????????????????B.??????????????????????????????????????????C.????????????????????????????????????????D.?π
4.正五边形的中心角等于( )
A.?18°???????????????????????????????????????B.?36°???????????????????????????????????????C.?54°???????????????????????????????????????D.?72°
5.半径为a的正六边形的面积等于( )
A.???????????????????????????????????B.???????????????????????????????????C.?a2?????????????????????????????????????D.?
6.等边三角形的内切圆半径,外接圆半径和高的比是(??? )
A.?????????????????????????????B.?2:3:4????????????????????????????C.?????????????????????????????D.?1:2:3
7.已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
A.?32﹣32﹣4π???????????????????????????????B.????????????????????????????????C.?1???????????????????????????????D.?16﹣4π
8.如果圆形纸片的直径是8cm,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
A.?2cm?????????????????????????????????B.?2cm??????????????????????????????????C.?4cm?????????????????????????????????D.?4Cm
9.如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是(?? )
A.???????????????????????????????????????B.?2 ??????????????????????????????????????C.???????????????????????????????????????D.?3
10.若一个圆的内接正三角形、正方形、正六边形的边心距分别为r1 , r2 , r3 , 则r1:r2:r3等于( )
A.?1:2:3?????????????????????????B.?::1?????????????????????????C.?1::?????????????????????????D.?3:2:1
二、填空题(共6题;共6分)
11.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=________.
12.如图,⊙O的半径为10,则⊙O的内接正三角形ABC的边长为________?.
13.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有________?.
14.如图, 是半径为2的圆内接正三角形,则图中阴影部分的面积是________ 结果用含 的式子表示 .
15.如图,⊙O的半径为1cm,正六边形ABCDEF内接于⊙O,则图中阴影部分面积为________cm2 . (结果保留π)
16.正六边形ABCDEF的边长为2,则对角线AE的长为________.
三、解答题(共4题;共25分)
17.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
18.如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;
(2)连接OF、OG,求∠OGF.
19.已知A、B两点,求作:过A、B两点的⊙O及⊙O的内接正六边形ABCDEF.(要求用直尺和圆规作图,保留作图痕迹,不必写作法及证明.)
20.如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
四、综合题(共4题;共47分)
21.如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
(1)求这个正六边形的边长.
(2)求这个正六边形的边心距.
(3)根据题意画出图形,根据圆的面积公式计算即可.
22.如图,已知正五边形AB CDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
23.如图,10-1、10-2、10-3、…、10-n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动
(1)求图10-1中∠APN的度数;
(2)图10-2中,∠APN的度数是________,图10-3中∠BPN的度数是________。
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
24.如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
答案
一、单选题
1.D 2.B 3.A 4.D 5.B 6.D 7.A 8.C 9.B 10.C
二、填空题
11.48° 12.10 13.10 14.15.16.?
三、解答题
17.解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD?cos45°=5×=5(cm).
即⊙O的半径R=5cm.
18.(1)解:设正六边形的边长为a,
则三角形OEF的边EF上的高为a,
则正六边形的面积为:6××a×a=a2 ,
∴正方形的面积为:a×a=a2 ,
∴正六边形与正方形的面积比a2:a2=3:2;
(2)解:∵OF=EF=FG,
∴∠OGF=(180°﹣60°﹣90°)=15°.
19.答:如图所示:
首先以AB为直径作圆,在以AB的一半为半径在圆上截取相等的弧,然后顺次连接六个等分点即可.
?
20.(1)解:∵DC=BC,
∴△CDB是等腰三角形,
∵∠C=108°,
∴∠1=∠CBD=36°,
∵AF∥CD,
∴∠F=∠1=36°,
可得四边形DEAB是等腰梯形,
∴∠DBA=∠2=72°,
∴∠F=∠BAF=36°,
∴△BAF是等腰三角形,
进而可得:∠GEA=∠G=∠2=72°,
∴△FDG,△AEG是等腰三角形,
故等腰三角形有:△BCD,△ABF,△FDG,△AEG.
(2)证明:∵五边形ABCDE是正五边形,
∴∠C=∠CDE=108°,CD=CB.
得∠1=36°,
∴∠2=108°﹣36°=72°.
又∵AF∥CD,
∴∠F=∠1=36°,
故∠G=180°﹣∠2﹣∠F=180°﹣72°﹣36°=72°=2∠F.
四、综合题
21.(1)解:∵正三角形的边长为6cm,
∴3个边长都相等,
又∵截去三个小等边三角形,
∴各个小三角形的边长也相等,
∴正六边形的边长为:2;
(2)解:连接OA,OB,过点O作OD⊥AB于点D,
∵∠AOB==60°,
∴△OAB是等边三角形,
∴OD=OA?sin60°=2×=;
(3)解:如图2:
线段AB划过的面积=π×22﹣π×()2=πcm2 .
22.(1)解:∵正五边形ABCDE
∴DC=BC,∠C=108°
∴△CDB是等腰三角形,
∴∠1=∠CBD=36°,
∵AF∥CD,
∴∠F=∠1=36°,
可得四边形DEAB是等腰梯形,
∴∠DBA=∠2=72°,
∴∠F=∠BAF=36°,
∴△BAF是等腰三角形,
同理可得:∠GEA=∠G=∠2=72°,
∴△FDG,△AEG是等腰三角形,
故等腰三角形有:△BCD,△ABF,△FDG,△AEG.
(2)证明:证明:∵五边形ABCDE是正五边形,
∴∠C=∠CDE=108°,CD=CB.
得∠1=36°,
∴∠2=108°?36°=72°.
又∵AF∥CD,
∴∠F=∠1=36°,
∴∠G=180°?∠2?∠F=180°?72°?36°=72°=2∠F,
23.(1)图1:∵点M、N分别从点B. C开始以相同的速度在O上逆时针运动,
∴劣弧BM=劣弧CN
∴∠BAM=∠CBN,
∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°。
(2)90°;108°
(3)由(1)、(2)可知,∠APN=它所在的正多边形的内角度数。
24.(1)证明:(1)连接OD.
∵四边形ABCD为正方形,AE=AB.
∴AE=AB=AD,∠EAD=∠DAB=90°,
∴∠EDA=45°,∠ODA=45°,
∴∠ODE=∠ADE+∠ODA=90°,
∴直线ED是⊙O的切线.
(2)证明:作OM⊥AB于M,
∵O为正方形的中心,
∴M为AB中点,
∴AE=AB=2AM,AF∥OM,
∴
∴EF=2FO.
(
1
)
同课章节目录
