3.8 弧长及扇形的面积一课一练(含答案)
文档属性
| 名称 | 3.8 弧长及扇形的面积一课一练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 204.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-13 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第8节)
一、单选题(共10题;共20分)
1.如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为(?? )
A.?????????????????????????????????????????B.???????????????????????C.?????????????????????????????????????????D.?
2.四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
A.?2π????????????????????????????????????????B.?4π????????????????????????????????????????C.?5π????????????????????????????????????????D.?6π
3.60°的圆心角所对的弧长是3πcm,则此弧所在圆的半径是( ???)
A.?6cm?????????????????????????????????????B.?7cm?????????????????????????????????????C.?8cm?????????????????????????????????????D.?9cm
4.如图,扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为( )
A.?3π?????????????????????????????????????B.?π?????????????????????????????????????C.?π?????????????????????????????????????D.?4π
5.如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径 ,则图中阴影部分的面积是(?? )
A.?﹣ ?????????????B.?﹣ ??????????????C.?﹣ ???????????????????????????D.?﹣
6.一扇形的半径等于已知圆的半径的2倍,且它的面积等于该圆的面积,则这一扇形的圆心角为(?? )
A.?20°?????????????????????????????????????B.?120°?????????????????????????????????????C.?100°?????????????????????????????????????D.?90°
7.如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为???(? ?? )
A.?16-4π???????????????????????????????B.?32-8π???????????????????????????????C.?8π-16???????????????????????????????D.?无法确定
8.在Rt△ABC中,斜边AB =4,∠B= 60°,将△ABC绕点B按顺时针方向旋转60°,顶点C运动的路线长是(?????)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?π?????????????????????????????????????????D.?
9.如图,在△ABC中,∠A=90?,AB=AC=2.以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E , 则图中阴影部分的面积是(?? )
A.?1-????????????????????????????????????B.?????????????????????????????????????C.?1-????????????????????????????????????D.?2-
10.用一个半径长为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面半径为? (??? )
A.?2 cm???????????????????????????????????B.?3 cm???????????????????????????????????C.?4 cm???????????????????????????????????D.?6 cm
二、填空题(共6题;共6分)
11.如图,在扇形纸片AOB中,OA=10,∠AOB=36°,OB在桌面内的直线l上.现将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转.则点O所经过的路线长为________
12.已知一扇形的圆心角为90°,弧长为6π,那么这个扇形的面积是________.
13.已知扇形的半径为4cm,圆心角为120°,则此扇形的弧长是________ cm
14.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 于点E,以点O为圆心,OC的长为半径作 交OB于点D.若OA=2,则阴影部分的面积为________.
15.如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为________.
16.如图,当半径为30cm的转动轮转过120°角时,传送带上的物体A平移的距离为________cm.
三、解答题(共4题;共20分)
17.用一个半径为4 cm,圆心角为120°的扇形纸片围成一个圆锥(接缝处不重叠),求这个圆锥的高.
18.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,CD=2, 求图中阴影部分的面积.
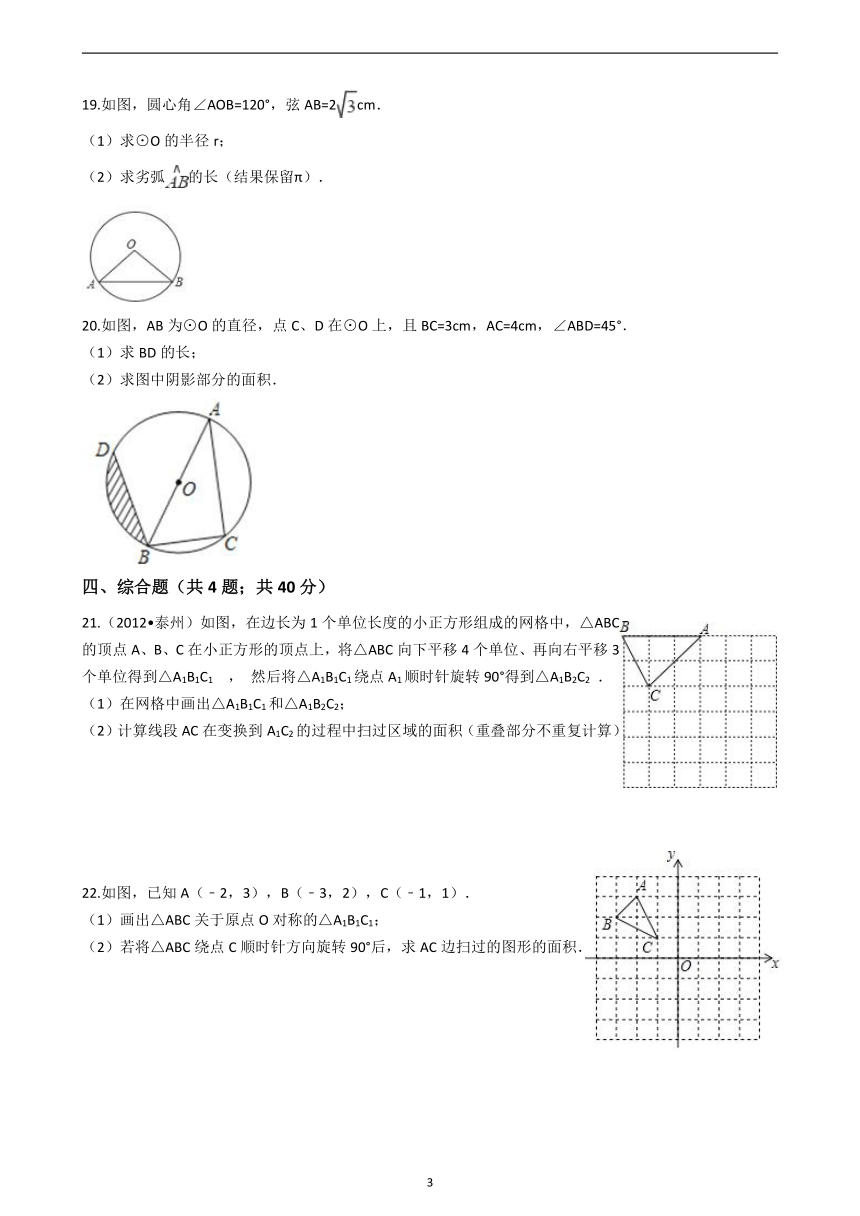
19.如图,圆心角∠AOB=120°,弦AB=2cm.
(1)求⊙O的半径r;
(2)求劣弧的长(结果保留π).
20.如图,AB为⊙O的直径,点C、D在⊙O上,且BC=3cm,AC=4cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
四、综合题(共4题;共40分)
21.(2012?泰州)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2 .
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC在变换到A1C2的过程中扫过区域的面积(重叠部分不重复计算)
22.如图,已知A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)若将△ABC绕点C顺时针方向旋转90°后,求AC边扫过的图形的面积.
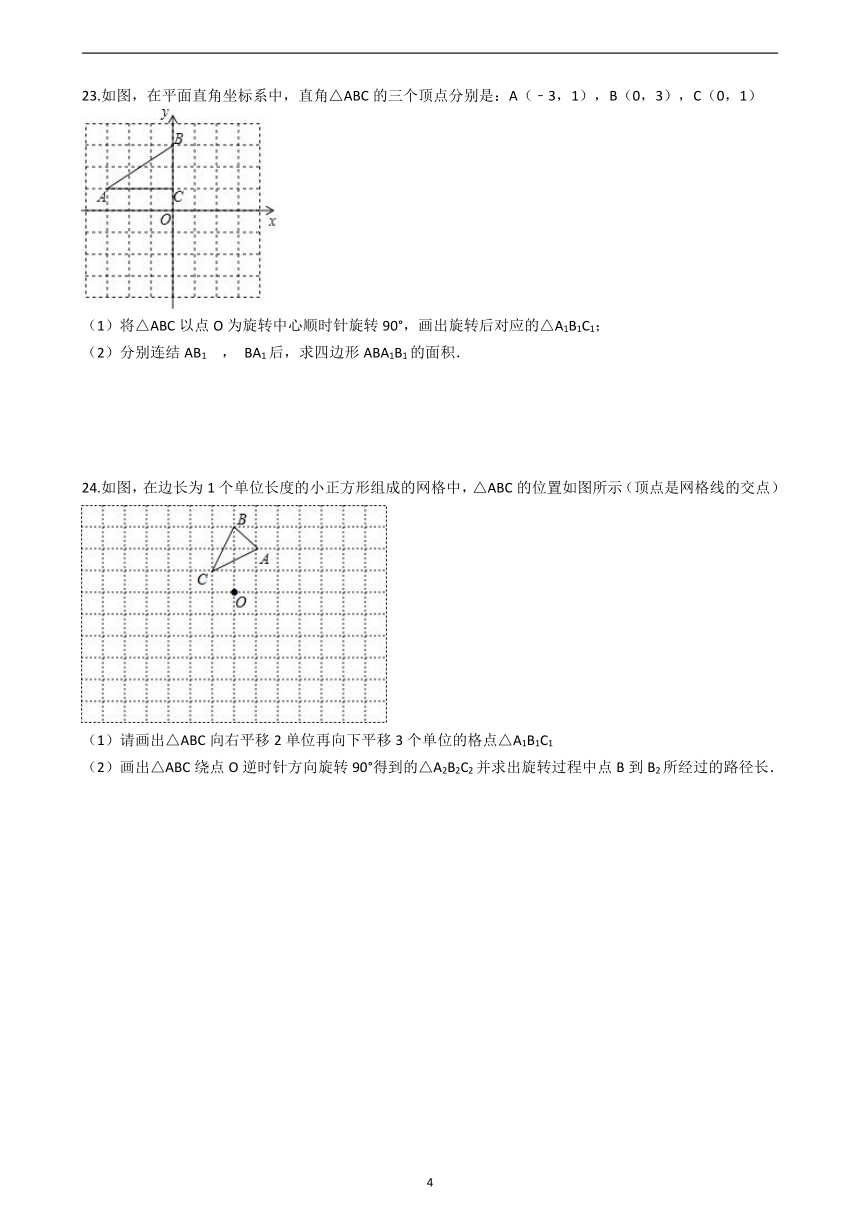
23.如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(﹣3,1),B(0,3),C(0,1)
(1)将△ABC以点O为旋转中心顺时针旋转90°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1 , BA1后,求四边形ABA1B1的面积.
24.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点)
(1)请画出△ABC向右平移2单位再向下平移3个单位的格点△A1B1C1
(2)画出△ABC绕点O逆时针方向旋转90°得到的△A2B2C2并求出旋转过程中点B到B2所经过的路径长.
答案
一、单选题
1.B 2.B 3.D 4.C 5.B 6.D 7.C 8.B 9.A 10.B
二、填空题
11.12π
12.36π
13.
14.+
15.
16.20π
三、解答题
17.解:扇形弧长为: l=cm,
设圆锥底面半径为r,
则:,所以,r=cm,
因为圆锥的高与底面半径、圆锥母线构成直角三角形的三边,
设圆锥高为h,所以h2+r2=42 ,
即:,h=cm,
所以圆锥的高为cm.
18.解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=.
∵∠CDB=30°,
∴∠COE=60°,
在Rt△OEC中,OC===2,
∵CE=DE,
∠COE=∠DBE=60°
∴Rt△COE≌Rt△DBE,
∴S阴影=S扇形OBC=π×OC2=π×4=π.
19.解:(1)作OC⊥AB于C,则AC=AB=cm.
∵∠AOB=120°,OA=OB∴∠A=30°.
∴在Rt△AOC中,r=OA==2cm.
(2)劣弧的长为:l=cm.
20.
解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=3cm,AC=4cm,
∴AB=5cm,
∴OB=2.5cm,
连OD,
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
∴BD==2.5cm.
(2)S阴影=π?(2.5)2﹣×2.5×2.5=cm2 .
四、综合题
21.(1)解:如图所示:
(2)解:∵图中是边长为1个单位长度的小正方形组成的网格, ∴AC= =2 ,
∵将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以2 为半径,圆心角为90°的扇形的面积,重叠部分是以A1为圆心,以2 为半径,圆心角为45°的扇形的面积,
∴线段AC在变换到A1C2的过程中扫过区域的面积=4×2+3×2+ ﹣ =14+π
22.(1)解:如图所示:△A1B1C1 , 即为所求
(2)解:如图,将△ABC绕点C顺时针方向旋转90°后, AC边扫过的部分的图形为扇形CA A',
根据勾股定理,CA= = ,
∴ .
23.(1)解:如图,△A1B1C1为所作;
(2)解:如图,四边形ABA1B1的面积= (1+3)×3+ ×(1+3)×3﹣ ×1×6=9
24.(1)解:如图;
(2)解:如图; 旋转过程中,点B到B2所经过的路径长为以OB为半径,90°为圆心角的弧长, = ×2π×3= π.
(
1
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册 第三章 圆的基本性质(第8节)
一、单选题(共10题;共20分)
1.如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为(?? )
A.?????????????????????????????????????????B.???????????????????????C.?????????????????????????????????????????D.?
2.四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
A.?2π????????????????????????????????????????B.?4π????????????????????????????????????????C.?5π????????????????????????????????????????D.?6π
3.60°的圆心角所对的弧长是3πcm,则此弧所在圆的半径是( ???)
A.?6cm?????????????????????????????????????B.?7cm?????????????????????????????????????C.?8cm?????????????????????????????????????D.?9cm
4.如图,扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为( )
A.?3π?????????????????????????????????????B.?π?????????????????????????????????????C.?π?????????????????????????????????????D.?4π
5.如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径 ,则图中阴影部分的面积是(?? )
A.?﹣ ?????????????B.?﹣ ??????????????C.?﹣ ???????????????????????????D.?﹣
6.一扇形的半径等于已知圆的半径的2倍,且它的面积等于该圆的面积,则这一扇形的圆心角为(?? )
A.?20°?????????????????????????????????????B.?120°?????????????????????????????????????C.?100°?????????????????????????????????????D.?90°
7.如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为???(? ?? )
A.?16-4π???????????????????????????????B.?32-8π???????????????????????????????C.?8π-16???????????????????????????????D.?无法确定
8.在Rt△ABC中,斜边AB =4,∠B= 60°,将△ABC绕点B按顺时针方向旋转60°,顶点C运动的路线长是(?????)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?π?????????????????????????????????????????D.?
9.如图,在△ABC中,∠A=90?,AB=AC=2.以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E , 则图中阴影部分的面积是(?? )
A.?1-????????????????????????????????????B.?????????????????????????????????????C.?1-????????????????????????????????????D.?2-
10.用一个半径长为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面半径为? (??? )
A.?2 cm???????????????????????????????????B.?3 cm???????????????????????????????????C.?4 cm???????????????????????????????????D.?6 cm
二、填空题(共6题;共6分)
11.如图,在扇形纸片AOB中,OA=10,∠AOB=36°,OB在桌面内的直线l上.现将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转.则点O所经过的路线长为________
12.已知一扇形的圆心角为90°,弧长为6π,那么这个扇形的面积是________.
13.已知扇形的半径为4cm,圆心角为120°,则此扇形的弧长是________ cm
14.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 于点E,以点O为圆心,OC的长为半径作 交OB于点D.若OA=2,则阴影部分的面积为________.
15.如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为________.
16.如图,当半径为30cm的转动轮转过120°角时,传送带上的物体A平移的距离为________cm.
三、解答题(共4题;共20分)
17.用一个半径为4 cm,圆心角为120°的扇形纸片围成一个圆锥(接缝处不重叠),求这个圆锥的高.
18.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,CD=2, 求图中阴影部分的面积.
19.如图,圆心角∠AOB=120°,弦AB=2cm.
(1)求⊙O的半径r;
(2)求劣弧的长(结果保留π).
20.如图,AB为⊙O的直径,点C、D在⊙O上,且BC=3cm,AC=4cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
四、综合题(共4题;共40分)
21.(2012?泰州)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2 .
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC在变换到A1C2的过程中扫过区域的面积(重叠部分不重复计算)
22.如图,已知A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)若将△ABC绕点C顺时针方向旋转90°后,求AC边扫过的图形的面积.
23.如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(﹣3,1),B(0,3),C(0,1)
(1)将△ABC以点O为旋转中心顺时针旋转90°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1 , BA1后,求四边形ABA1B1的面积.
24.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点)
(1)请画出△ABC向右平移2单位再向下平移3个单位的格点△A1B1C1
(2)画出△ABC绕点O逆时针方向旋转90°得到的△A2B2C2并求出旋转过程中点B到B2所经过的路径长.
答案
一、单选题
1.B 2.B 3.D 4.C 5.B 6.D 7.C 8.B 9.A 10.B
二、填空题
11.12π
12.36π
13.
14.+
15.
16.20π
三、解答题
17.解:扇形弧长为: l=cm,
设圆锥底面半径为r,
则:,所以,r=cm,
因为圆锥的高与底面半径、圆锥母线构成直角三角形的三边,
设圆锥高为h,所以h2+r2=42 ,
即:,h=cm,
所以圆锥的高为cm.
18.解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=.
∵∠CDB=30°,
∴∠COE=60°,
在Rt△OEC中,OC===2,
∵CE=DE,
∠COE=∠DBE=60°
∴Rt△COE≌Rt△DBE,
∴S阴影=S扇形OBC=π×OC2=π×4=π.
19.解:(1)作OC⊥AB于C,则AC=AB=cm.
∵∠AOB=120°,OA=OB∴∠A=30°.
∴在Rt△AOC中,r=OA==2cm.
(2)劣弧的长为:l=cm.
20.
解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=3cm,AC=4cm,
∴AB=5cm,
∴OB=2.5cm,
连OD,
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
∴BD==2.5cm.
(2)S阴影=π?(2.5)2﹣×2.5×2.5=cm2 .
四、综合题
21.(1)解:如图所示:
(2)解:∵图中是边长为1个单位长度的小正方形组成的网格, ∴AC= =2 ,
∵将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以2 为半径,圆心角为90°的扇形的面积,重叠部分是以A1为圆心,以2 为半径,圆心角为45°的扇形的面积,
∴线段AC在变换到A1C2的过程中扫过区域的面积=4×2+3×2+ ﹣ =14+π
22.(1)解:如图所示:△A1B1C1 , 即为所求
(2)解:如图,将△ABC绕点C顺时针方向旋转90°后, AC边扫过的部分的图形为扇形CA A',
根据勾股定理,CA= = ,
∴ .
23.(1)解:如图,△A1B1C1为所作;
(2)解:如图,四边形ABA1B1的面积= (1+3)×3+ ×(1+3)×3﹣ ×1×6=9
24.(1)解:如图;
(2)解:如图; 旋转过程中,点B到B2所经过的路径长为以OB为半径,90°为圆心角的弧长, = ×2π×3= π.
(
1
)
同课章节目录
