4.6 相似多边形课时作业

4.6 相似多边形课时作业
姓名：__________班级：__________考号：__________
一 、选择题
1. “相似的图形”是（　　）
A．形状相同的图形 B．大小不相同的图形
C．能够重合的图形 D．大小相同的图形
2.制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是（　　）
A． 360元 B． 720元 C． 1080元 D． 2160元
3.若两个相似矩形的相似比为，较小矩形面积为，较大矩形一边为，则其相邻的一边是（ ）
A． B． C． D．
4.下列结论中正确的是（　　）
A．有两条边长是3和4的两个直角三角形相似
B．一个角对应相等的两个等腰三角形相似
C．两边对应成比例且一个角对应相等的两个三角形相似
D．有一个角为60°的两个等腰三角形相似
5.下列各组图形不一定相似的是（???）
A．两个等腰直角三角形 B．各有一个角是100°的两个等腰三角形
C．两个矩形 D．各有一个角是50°的两个直角三角形
6.如果整张纸与半张纸相似，则整张纸的长和宽的比是( )
A． B． C． D．
二、填空题
7.下列说法中：
①所有的等腰三角形都相似；
②所有的正三角形都相似；
③所有的正方形都相似；
④所有的矩形都相似．
其中说法正确的序号是　 　．
8.如图，有两个形状相同的星星图案，则x的值为______．
9.有一个多边形的边长分别是4cm，5cm，6cm，4cm，5cm，和它相似的一个多边形最长边为8cm，那么这个多边形的周长是_________.
10.我们通常用到的一种复印纸，整张称为纸（如图），按下图方式对折一分为二裁开成为纸（如图），再一分为二成为纸（如图）…它们都是相似的矩形，这些矩形的长与宽的比值都是一定值，这个定值是________．
11.如图，正方形的边长是，除，，和四点外，图形的其他顶点均为所在的一条线段的中点，则从正方形中挖掉阴影部分后，所剩下部分面积等于________．
三、解答题
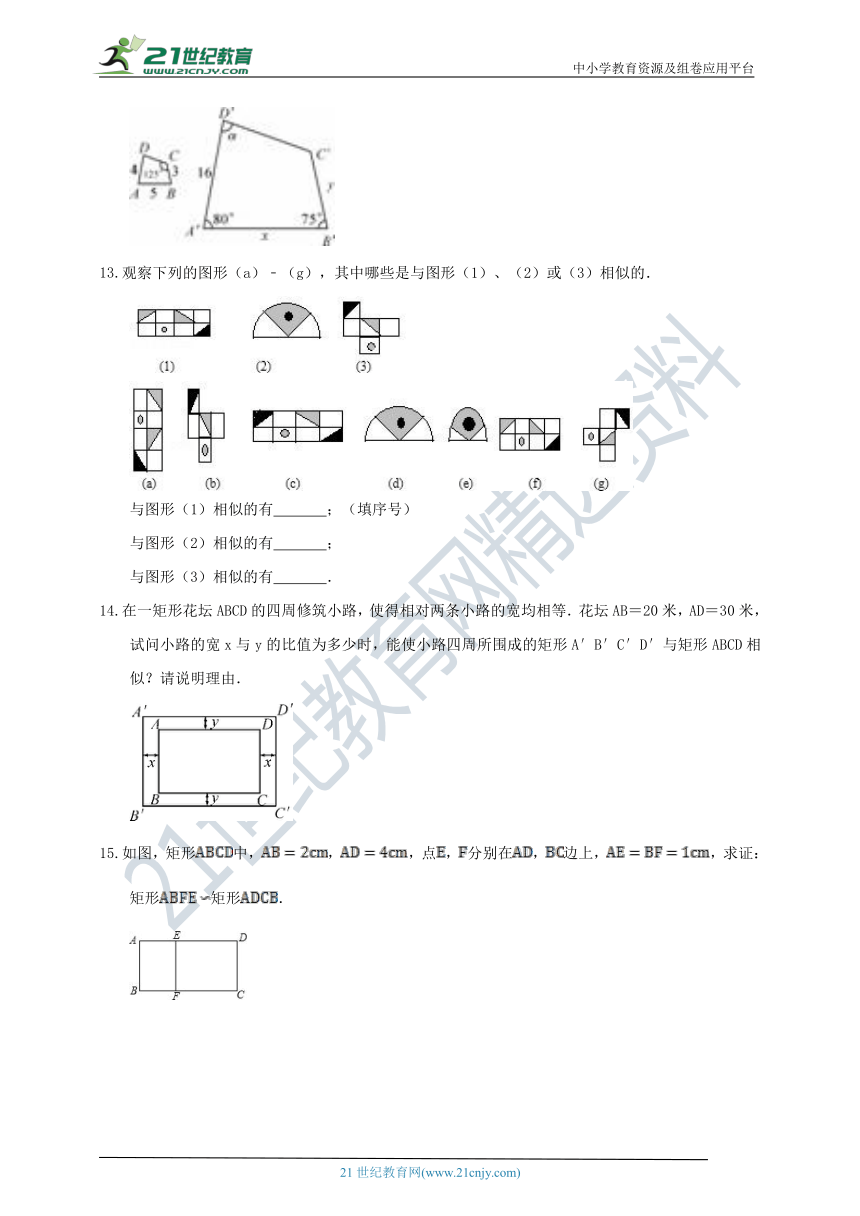
12.在如图所示的两个相似的四边形中，求x，y，∠α的值．
13.观察下列的图形（a）﹣（g），其中哪些是与图形（1）、（2）或（3）相似的．
与图形（1）相似的有　 　；（填序号）
与图形（2）相似的有　 　；
与图形（3）相似的有　 　．
14.在一矩形花坛ABCD的四周修筑小路，使得相对两条小路的宽均相等．花坛AB＝20米，AD＝30米，试问小路的宽x与y的比值为多少时，能使小路四周所围成的矩形A′B′C′D′与矩形ABCD相似？请说明理由．
15.如图，矩形中，，，点，分别在，边上，，求证：矩形矩形．
答案解析
一 、选择题
1.【考点】相似图形
【分析】根据相似形的定义直接进行判断即可．
解：相似图形是形状相同的图形，大小可以相同，也可以不同，
故选：A．
【点评】本题考查了相似图形的定义，解题的关键是了解相似图形是形状相同的图形，难度不大．
2.【考点】相似多边形的性质
【分析】根据题意求出长方形广告牌每平方米的成本，根据相似多边形的性质求出扩大后长方形广告牌的面积，计算即可．
解：3m×2m=6m2，
∴长方形广告牌的成本是120÷6=20元/m2，
将此广告牌的四边都扩大为原来的3倍，
则面积扩大为原来的9倍，
∴扩大后长方形广告牌的面积=9×6=54m2，
∴扩大后长方形广告牌的成本是54×20=1080m2，
故选C．
【点睛】本题考查的是相似多边形的性质，掌握相似多边形的面积比等于相似比的平方是解题的关键．
【考点】相似多边形的性质
【分析】根据相似多边形的性质得到两个相似矩形的面积比为4：1，而较小矩形面积为3cm2，可得到较大矩形的面积，然后根据矩形的面积公式已知一边长易求出另一边长．
解：∵两个相似矩形的相似比为2:1，
∴两个相似矩形的面积比为4:1，
而较小矩形面积为3cm2，
∴较大矩形的面积=4×3=12cm2，
又∵较大矩形一边为2，
∴较大矩形另一边=12÷2=6(cm).
故选:B.
【点睛】考查相似多边形的性质，相似多边形的面积比等于相似比的平方.
【考点】相似图形
【分析】根据相似三角形的判定方法即可判断；
解：A、错误．比如，一个直角三角形的直角边为3，4，另一个直角三角形的一条直角边为3，斜边为4，这两个直角三角形不相似；
B、错误．当这个角一个是等腰三角形的顶角，一个是等腰三角形的底角，两个等腰三角形不相似；
C、错误；边对应成比例且一个角对应相等的两个三角形不一定相似；
D、正确．两个等边三角形相似；
故选：D．
【点评】本题考查相似三角形的判定，矩形的相似的判定等知识，解题的关键是熟练掌握相似三角形的判定方法，矩形的相似的判定方法，属于中考常考题型．
【分析】根据相似图形的定义，对应边成比例，对应角相等对各选项分析判断。
解：A、两个等腰直角三角形，对应边成比例，对应角相等，符合定义，一定相似，故正确；
B、各有一个角是100°的两个等腰三角形，100°的角一定是顶角，其余两角一定相等，故一定相似，故正确；
C、两个矩形，四个角都是直角，但四条边不一定对应成比例，不一定相似，故错误；
D、各有一个角是50°的两个直角三角形，都有一个直角，根据两角对应相等，两三角形相似，故正确。
故选C
【考点】相似多边形的性质
【分析】根据相似形对应边的比相等，列式即可得出长与宽的比．
解：设报纸的长为2x，报纸的宽为y，
∵整张报纸与半张报纸相似，
则；即；
2x：y＝：1．
故选：B．
【点睛】本题考查相似多边形的性质．相似多边形对应边之比等于相似比．
二 、填空题
【考点】相似图形
【分析】根据正方形、矩形、等边三角形、等腰三角形的性质进行判断即可．
解：①所有的等腰三角形都相似，错误；
②所有的正三角形都相似，正确；
③所有的正方形都相似，正确；
④所有的矩形都相似，错误．
故答案为：②③．
【点评】本题考查了相似图形的知识，熟练掌握各特殊图形的性质是解题的关键，难度一般．
【考点】相似多边形的性质
【分析】根据相似多边形的性质：对应线段的比等于相似比列式求解即可.
解：由题意得，
15:20=6:x,
∴x=8.
故答案为：8.
【点睛】本题考查了相似多边形的性质，如果两个多边形相似，那么它们对应边的比相等，对应角相等，对应周长的比都等于相似比；它们对应面积的比等于相似比的平方.
【考点】相似多边形的性质
【分析】先根据两多边形相似求出其相似比，再根据相似多边形周长的比等于相似比进行解答．
解：∵一个多边形的边长分别是4cm、5cm、6cm、4cm、5cm，和它相似的一个多边形最长边为8cm，
∴两个相似多边形的相似比
∴
解得C=32cm.
故答案为：32cm.
【点睛】考查相似多边形的性质，掌握周长比等于相似比是解题的关键.
【考点】相似多边形的性质
【分析】分别设A1纸的长为a，宽为b，A2纸的长为b，宽为再由相似多边形的对应边成比例列出比例式，求出的值即可．
解：设A1纸的长为a，宽为b，A2纸的长为b，宽为，由A1、A2纸的长与宽对应比成比例得=，
故==．
故答案为：．
【点睛】本题考查的是相似多边形的性质，即相似多边形的对应边成比例．
【考点】相似多边形的性质
【分析】由题意易得，正方形ABCD与阴影部分是相似正方形，且相似比为4：1，则面积比为16：1，据此求解．
解：由题意得，正方形ABCD与阴影部分是相似正方形，且相似比为4：1，则面积比为16：1，
∵SABCD=a2，
∴S阴影=
∴所求的剩下的部分的面积是a2?
故答案为：
【点睛】考查相似多边形的性质，相似多边形的面积比等于相似比的平方.
三 、解答题
【考点】相似多边形的性质
【分析】根据相似多边形对应角相等，对应边的比相等进行求解即可得.
解：∵四边形ABCD∽四边形A′B′C′D′，
∴，∠C′=∠C=125°，
即，
∴x=20，y=12，
在四边形A′B′C′D′，α=360°-∠A′-∠B′-∠C′=360°-80°-75°-125°=80°.
【点睛】本题考查了相似多边形的性质，熟练掌握相似多边形的性质是解题的关键.
【考点】相似图形
【分析】根据相似图形的定义，结合图形，通过比较得到正确结果．
解：观察比较图形，根据相似形的定义可知：
与图形（1）相似的有a；
与图形（2）相似的有d；
与图形（3）相似的有g．
【点评】本题考查的是相似形的定义，即图形的形状相同，但大小不一定相同的变换是相似变换．
【考点】相似多边形的性质
【分析】由题可知矩形A′B′C′D′与矩形ABCD相似,根据对应边成比例,列方程即可解答.
解：由题意有＝，
从而有20(30＋2x)＝30(20＋2y)，
解得＝，即x与y的比值为3∶2时，
能使矩形A′B′C′D′与矩形ABCD相似.
【点睛】本题主要是把实际问题抽象到相似多边形中,利用相似多边形对应边的比相等,列出方程,即可得出x;y的比值.
【考点】相似多边形的定义
【分析】根据矩形的性质得出∠A=∠B=∠C=∠D=90°，AB=CD=2cm，AD=BC=4cm，AD∥BC，求出四边形AEFB是矩形，推出∠AEF=∠EFB=90°，AB=EF=2cm，求出∠A=∠A，∠AEF=∠B，∠B=∠D，∠EFB=∠C，，根据多边形相似的判定定理推出即可．
证明：∵四边形是矩形，
∴，，，，
即，
∵，
∴四边形是矩形，
∴，，
∴，，，，，
∴矩形矩形．
【点睛】本题考查了矩形的性质和判定，相似多边形的定义定理的应用，能求出∠A=∠A、∠AEF=∠B、∠B=∠D、∠EFB=∠C、是解此题的关键，难度适中．