5.4 一次函数的图象(1)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 5.4 一次函数的图象(1)(知识清单+经典例题+夯实基础+提优训练+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 14:35:53 | ||
图片预览




文档简介
浙江版八年级数学上册第5章5.4一次函数图象
第1课时 一次函数图象(1)
【知识清单】
一、函数的图像:
把一个函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做这个函数的图象.
二、描点法画函数图形的一般步骤:
第一步:列表(表中给出一些自变量的值及其对应的函数值);
第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);
第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来).
三、一次函数y=kx+b(k、b为常数, k≠0)的图象的画法:
根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.
一般情况下:
(1)画正比例函数y=kx(k≠0)的图象时,只要描出点(0,0),(1,k)即可;
(2)画一次函数y=kx+b(k、b为常数, k≠0)的图象时只要描出点(0,b),.即描出直线与坐标轴的交点坐标即可.
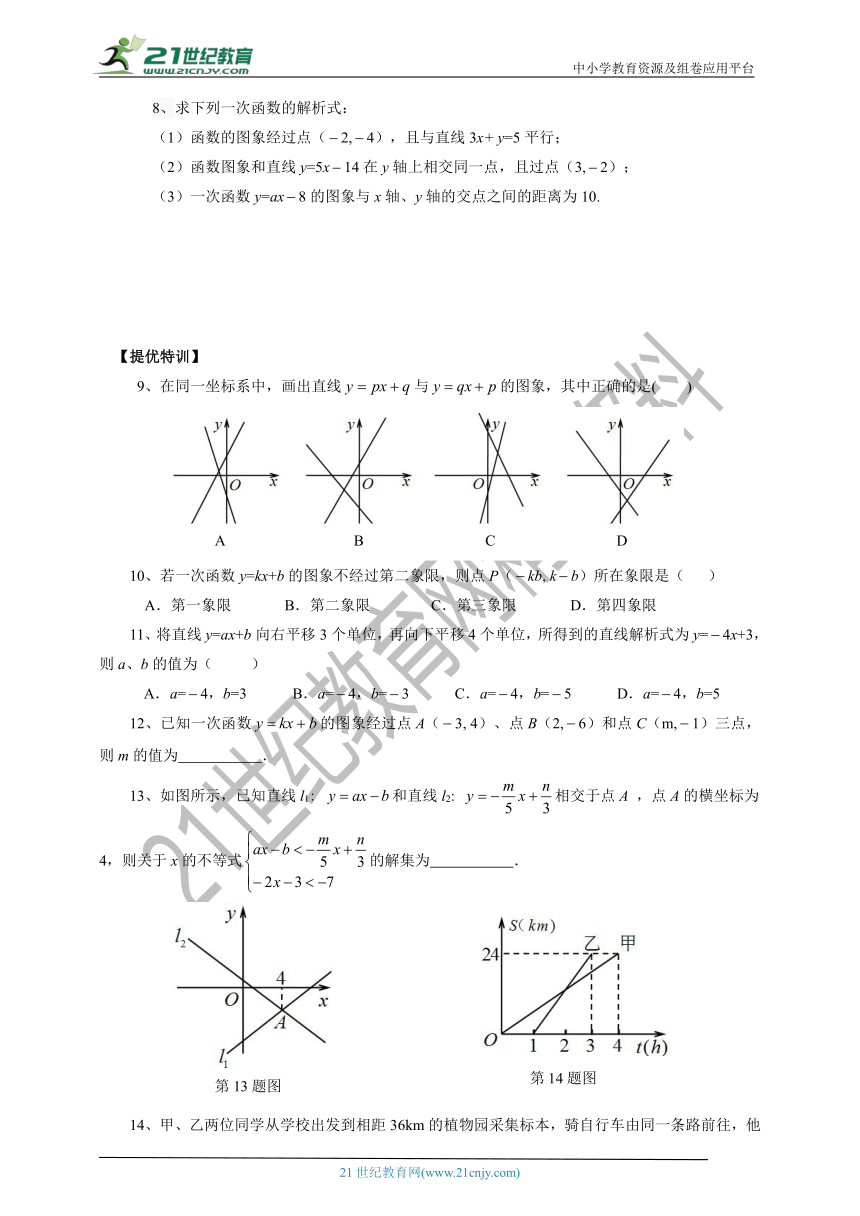
四、一次函数y=kx+b中,k、b的取值决定直线的位置:
b>0
b<0
b=0
k>0
经过第一、二、三象限
经过第一、三、四象限
经过第一、三象限
k<0
经过第一、二、四象限
经过第二、三、四象限
经过第二、四象限
五、正比例函数与一次函数之间的关系(直线的平移)
(1)左右平移:图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小.左右平移的规律:左加右减 .
(2)上下平移:一次函数y=kx+b的图象是一条直线,它可以看作是由直线y=kx平移|b|个单位长度而得到(当b>0时,向上平移;当b<0时,向下平移).图像的上下平移与k无关,与b有关,图像向上移动b的值增加,图像向下移动b的值减小.上下平移的规律:上加下减 .
六、直线()与()的位置关系
(1)两直线平行且
(2)两直线相交(特殊情况,时,两直线于y轴的(0,b1).
(3)两直线重合且
(4)两直线垂直
七、两条直线的交点坐标的求法:
把两条直线的解析式联立成二元一次方程组,求出方程组的解,把函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标即可.
【经典例题】
例题1、若mn>0,np<0,则直线经过象限是( ).
A.第一、二、四象限 B.第二、三、四象限
C.第一、三、四象限 D.第一、二、三象限
【考点】一次函数图象与系数的关系.
【分析】先根据已知条件判断出及的符号,再根据一次函数的图象经过(或不经过)的象限与系数的关系解答即可.
【解答】∵mn>0,np<0,
∴m与n同号,n与p异号,
∴,,
∴.
∴直线经过第一、三、四象限.故选C
【点评】本题考查的是一次函数的图象与系数的关系,根据已知条件判断出m、n、p的符号关系是解答此题的关键.
例题2、已知一次函数y=kx+b的图象经过点A(0,2)和点B(2,4).
(1)求函数是解析式,并画出它的图象;
(2)试判定点(1,2)和点是否在函数图象上,点(m,3m+2)呢?
(3)当x>3时,求y的取值范围.
【考点】待定系数法求一次函数解析式、一次函数的图象以及由自变量的取值范围推出因变量的取值范围.
【分析】(1)设此直线的解析式为y=kx+b(k≠0),把点A(0,2)和点B(2,4)代入y=kx+b即可求出k、b的值,进而得出此函数的解析式;在直角坐标系内描出点A(0,2)和点B(2,4),画出过此两点的直线即可(也可以描出直线与x轴和y轴的交点坐标);
(2) 把点(1,2)和点以及(m,3m+2)分别代入y=kx+b进行验证即可;
(3) 把y=kx+b化成用含y的代数式表示x,再根据x>3,求出y的取值范围即可.
【解答】(1)设直线的解析式为(k≠0),
把点A(0,2)和点B(2,4)代入y=kx+b得,
,
解得,
故此直线的解析式为:;
在坐标系内描出点A(0,2)和点B(2,4),作出过A、B两点的直线如图所示.
(2) 把点(1,2)和点以及(m,3m+2)分别代入进行验证,
当x=1时,,
所以点(1,2)不在函数图象上;
当x=时,,
所以点在函数图象上;
当x=时,,
所以点(m,3m+2)在函数图象上.
(3)∵,
∴.
∵x>3,
∴,解得,y<7.
∴当x>3时, y的取值范围是y<7.
【点评】本题考查的是用待定系数法求一次函数的解析式、画一次函数的图象以及判断一个点是否在直线上的能力和技巧,根据题意得出关于k、b的方程组是解答此题的关键.
【夯实基础】
1、下列表示一次函数y=2x+4的图象的是( )
2、如图,把直线沿x轴负方向向左平移4个单位,得到直线,则直线的解析式为 (???? )
A. ???? ? B. ??????
C.????? D.
3、函数y=3x6的图象经过的象限正确的是( )
A.第一、二、四象限 B.第二、三、四象限
C.第一、三、四象限 D.第一、二、三象限
4、直线与相交于点(4,5),且两直线与y轴围成的三角形的面积为16,那么b1b2的值为( )
A.8 B.16 C.32 D.无法确定
5、已知一次函数y=2kx(2k6)的图象经过原点,则函数的解析式是 .
6、如图直线y=mx+n过A(3,0)和点B(0,2),则关于x的方程mx+n=0的解为__ _______.
7、求下列函数与x轴和y轴的交点坐标,并在同一坐标系中画出它们的图象.
(1)①;
②;
(2)求两条直线与x轴所围成的△ABC的面积.
8、求下列一次函数的解析式:
(1)函数的图象经过点(2,4),且与直线3x+ y=5平行;
(2)函数图象和直线y=5x14在y轴上相交同一点,且过点(3,2);
(3)一次函数y=ax8的图象与x轴、y轴的交点之间的距离为10.
【提优特训】
9、在同一坐标系中,画出直线与的图象,其中正确的是( )
10、若一次函数y=kx+b的图象不经过第二象限,则点P(kb, kb)所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11、将直线y=ax+b向右平移3个单位,再向下平移4个单位,所得到的直线解析式为y=4x+3,则a、b的值为( )
A.a=4,b=3 B.a=4,b=3 C.a=4,b=5 D.a=4,b=5
12、已知一次函数的图象经过点A(3, 4)、点B(2,6)和点C(m,1)三点,则m的值为 .
13、如图所示,已知直线l1: 和直线l2: 相交于点A ,点A的横坐标为4,则关于x的不等式的解集为 .
14、甲、乙两位同学从学校出发到相距36km的植物园采集标本,骑自行车由同一条路前往,他们离出发地的距离s(km)和行驶时间t(h)之间的函数图象如图所示.根据图中提供的信息:有以下论断①乙同学比甲同学晚出发1(h);②乙同学出发1(h)追上甲同学;③甲同学的速度比乙同学的速度快;④乙同学到达目的地时,甲同学离目的地还有9km的路程. 符合图象描述的说法是 .(写出序号即可)
15、已知函数的图象不经过第一象限,且m为整数,则函数的解析式是 ,若此函数的图象与x轴、y轴分别交于A、B两点,则△AOB的面积为 ,把△AOB绕点A逆时针旋转90°后得到 ,则点的坐标是 .
16、已知一次函数y=3ax+9与y=2xb的图象都经过点A(2,3),且与x轴分别交于点B、C,求:
(1)求点B、C的坐标;
(2)求△ABC的面积.
17、如图,直线与x轴、y轴分别交于A、B两点,另一条直线经过点B,且与线段OA相交于点C,若直线将△AOB的面积分成1︰2的两部分,求直线的解析式.
18、如图,在平面直角坐标系中,点A的坐标为(2,5),点B的坐标为(4,3).请你在x轴上找一点P,使PA+PB的值最小.
(1)求点P的坐标;(2)求PA+PB的最小值.
【中考链接】
19.2018?甘肃定西16.(3分)如图,一次函数y=x2与y=2x+m的图象相交于点P(n,4),则关于x的不等式组的解集为 -220、2018年湖南娄底将直线y=2x3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )
A.y=2x4 B.y=2x+4 C.y=2x+2 D.y=2x2
21、2018?广西桂林12. 如图,在平面直角坐标系中,M、N、C三点的坐标分别为(,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A. B. C. D.
22、2018黑龙江龙东地区25.(8.00分)某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 20 吨,a= 15 .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
参考答案
1、B 2、C 3、B 4、A 5、, 6、 9、C 10、D 11、C 12、
13、 14、①、②、④ 15、、 、 19、
20、A 21、A
7、解:(1)①∵,
∴令x=0,y=6,则直线与y轴的交点坐标为(0,6).
∴令y=0,x=2,则直线与x轴的交点坐标为(2,0).
过点(2,0)和点(0,6)画出直线即可;
∵②,
∴令x=0,y=6.
则直线与y轴的交点坐标为(0, 6).
∴令y=0,x=4,
则直线与x轴的交点坐标为(4,0).
过点(4,0)和点(0, 6)画出直线即可;
所画的图象如图所示.
(3)∵直线和直线的相交于点A,
∴可得方程组,
∴解方程组,得,
∴点A的坐标为,点A到x轴的距离为2.
∵点B的坐标为(2,0)、点C的坐标为(4,0),
∴BC=42=2,
∴△ABC的面积=.
8、解:(1)设所求一次函数的解析式为y1=kx+b,
∵3x+ y=5,
∴y=3x+5.
∵y1∥y,
∴k=3.
∴y1=3x+b.
把点(2,4)代入y1=3x+b得,
4=3×(2)+b,
解得b=10.
∴所求一次函数的解析式为y1=3x10.
(2)令x=0, y=14,
∴直线y=5x14与y轴的交点坐标(0, 14).
∵所求直线与直线y=5x14在y轴上相交同一点,
∴设所求直线的解析式为y=kx14.
把点(3,2)代入y=kx14得,
2=3k14,
解得k =4.
∴所求一次函数的解析式为y=4x14.
(3)根据题意,得a≠0, 且一次函数y=ax8的图象与x轴、y轴的交点坐标分别为
、(0,8),
由勾股定理,得,
解得,
∴所求一次函数的解析式为.
16、解:(1)把点A(2,3)分别代入一次函数y=3ax+9与y=2xb中,
3=3×(2)a+9,3=2×(2)b,
解得a=2,b=7.
所以一次函数解析式分别为y=6x+9、y=2x7.
令y=0,则6x+9=0、2x7=0,
解得、.
所以点B的坐标为,点C的坐标为.
(2) ∵直线y=6x+9与y=2x7相交于A(2,3),
∴点A的x轴的距离为.
∵点B的坐标为,点C的坐标为,
∴.
∴△ABC的面积=.
17、解:如图①∵直线与x轴、y轴分别交于A、B两点,
∴令x=0,y=2,则点B的坐标为(0,2).
∴令y=0,x=12,则点A的坐标为(12,0).
直线将△AOB的面积分成1︰2的两部分,
(1)如图②S△ABC=2 S△CBO,
∵△ABC与△CBO是同高的三角形,
∴AC=2OC.
∴OC+2OC=OA=12,
∴OC=4.
∴点C的坐标为(4,0).
将点B(0,2)和点C(4,0)分别代入得,
,解得,.
∴函数的解析式为;
(2)如图③S△CBO =2 S△ABC,
∵△ABC与△CBO是同高的三角形,
∴OC =2 AC.
∴,
∴OC=8.
∴点C的坐标为(8,0).
将点B(0,2)和点C(8,0)分别代入得,
, 解得,.
∴函数的解析式为.
∴直线的解析式为或.
18、解如图,(1)①作出点A关于x轴的对称点A′(2,5),点D是垂足,
②连结A′B,交x轴于点P,点P就是要求的点.
③设直线A′B的解析式为y=kx+b,
把点A′(2,5)、点B(4,3)代入y=kx+b,
得,解得,.
∴直线A′B的解析式为.
令y=0,则,
解得,,
∴点P的坐标为.
(2)过B作BC⊥x轴,点C是垂足,过A′作A′E⊥y轴,点E是垂足,
延长BC、A′E相交于点Q,则Q的坐标为(4,5).由对称性可知AP=A′P,PAPB= PA′PB=A′B;
∴A′B最短,(两点之间,线段最短),即AP+PB最小,
∴在Rt△A′QB中,A′Q=6,QB=8,
∴
即PA+PB的最小值为10.
也可利用两点之间的距离公式求
将点B(4,3),点A′(2,5)代入公式,
.
21、【答案】A
【解析】分析:分别求出当点A与点M、N重合时直线AC的解析式,由AB⊥AC可得直线AB的解析式,从而求出b的值,最终可确定b的取值范围.
【解答】:当点A与点N重合时,MN⊥AC,
∴MN是直线AB的一部分,
∵N(3,1)
∴此时b=1;
当点A与点M重合时,设直线AC的解析式为y=k1x+m,
由于AC经过点A、C两点,故可得,解得:,
设直线AB的解析式为y=k2x+b,
∵AB⊥AC,
∴,
∴.
故直线AB的解析式为y=x+b,
把(,1)代入y=x+b得, b=.
∴b的取值范围是.
故选A.
点睛:此题考查一次函数基本性质,待定系数求解析式,简单的几何关系.
22、【分析】(1)根据题意,由图2得出两个车间同时加工和甲单独加工的速度;
(2)用待定系数法解决问题;
(3)求出两个车间每天加工速度分别计算两个55吨完成的时间.
【解答】解:(1)由图象可知,第一天甲乙共加工220185=35吨,第二天,乙停止工作,甲单独加工185165=20吨,
则乙一天加工3520=15吨.a=15
故答案为:20,15
(2)设y=kx+b
把(2,15),(5,120)代入
,解得,,
∴y=35x55.
(3)由图2可知
当w=220﹣55=165时,恰好是第二天加工结束.
当2≤x≤5时,两个车间每天加工速度为=55吨
∴再过1天装满第二节车厢
【点评】本题为一次函数实际应用问题,应用了待定系数法.解答要注意通过对边两个函数图象实际意义对比分析得到问题答案.
第1课时 一次函数图象(1)
【知识清单】
一、函数的图像:
把一个函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做这个函数的图象.
二、描点法画函数图形的一般步骤:
第一步:列表(表中给出一些自变量的值及其对应的函数值);
第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);
第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来).
三、一次函数y=kx+b(k、b为常数, k≠0)的图象的画法:
根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.
一般情况下:
(1)画正比例函数y=kx(k≠0)的图象时,只要描出点(0,0),(1,k)即可;
(2)画一次函数y=kx+b(k、b为常数, k≠0)的图象时只要描出点(0,b),.即描出直线与坐标轴的交点坐标即可.
四、一次函数y=kx+b中,k、b的取值决定直线的位置:
b>0
b<0
b=0
k>0
经过第一、二、三象限
经过第一、三、四象限
经过第一、三象限
k<0
经过第一、二、四象限
经过第二、三、四象限
经过第二、四象限
五、正比例函数与一次函数之间的关系(直线的平移)
(1)左右平移:图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小.左右平移的规律:左加右减 .
(2)上下平移:一次函数y=kx+b的图象是一条直线,它可以看作是由直线y=kx平移|b|个单位长度而得到(当b>0时,向上平移;当b<0时,向下平移).图像的上下平移与k无关,与b有关,图像向上移动b的值增加,图像向下移动b的值减小.上下平移的规律:上加下减 .
六、直线()与()的位置关系
(1)两直线平行且
(2)两直线相交(特殊情况,时,两直线于y轴的(0,b1).
(3)两直线重合且
(4)两直线垂直
七、两条直线的交点坐标的求法:
把两条直线的解析式联立成二元一次方程组,求出方程组的解,把函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标即可.
【经典例题】
例题1、若mn>0,np<0,则直线经过象限是( ).
A.第一、二、四象限 B.第二、三、四象限
C.第一、三、四象限 D.第一、二、三象限
【考点】一次函数图象与系数的关系.
【分析】先根据已知条件判断出及的符号,再根据一次函数的图象经过(或不经过)的象限与系数的关系解答即可.
【解答】∵mn>0,np<0,
∴m与n同号,n与p异号,
∴,,
∴.
∴直线经过第一、三、四象限.故选C
【点评】本题考查的是一次函数的图象与系数的关系,根据已知条件判断出m、n、p的符号关系是解答此题的关键.
例题2、已知一次函数y=kx+b的图象经过点A(0,2)和点B(2,4).
(1)求函数是解析式,并画出它的图象;
(2)试判定点(1,2)和点是否在函数图象上,点(m,3m+2)呢?
(3)当x>3时,求y的取值范围.
【考点】待定系数法求一次函数解析式、一次函数的图象以及由自变量的取值范围推出因变量的取值范围.
【分析】(1)设此直线的解析式为y=kx+b(k≠0),把点A(0,2)和点B(2,4)代入y=kx+b即可求出k、b的值,进而得出此函数的解析式;在直角坐标系内描出点A(0,2)和点B(2,4),画出过此两点的直线即可(也可以描出直线与x轴和y轴的交点坐标);
(2) 把点(1,2)和点以及(m,3m+2)分别代入y=kx+b进行验证即可;
(3) 把y=kx+b化成用含y的代数式表示x,再根据x>3,求出y的取值范围即可.
【解答】(1)设直线的解析式为(k≠0),
把点A(0,2)和点B(2,4)代入y=kx+b得,
,
解得,
故此直线的解析式为:;
在坐标系内描出点A(0,2)和点B(2,4),作出过A、B两点的直线如图所示.
(2) 把点(1,2)和点以及(m,3m+2)分别代入进行验证,
当x=1时,,
所以点(1,2)不在函数图象上;
当x=时,,
所以点在函数图象上;
当x=时,,
所以点(m,3m+2)在函数图象上.
(3)∵,
∴.
∵x>3,
∴,解得,y<7.
∴当x>3时, y的取值范围是y<7.
【点评】本题考查的是用待定系数法求一次函数的解析式、画一次函数的图象以及判断一个点是否在直线上的能力和技巧,根据题意得出关于k、b的方程组是解答此题的关键.
【夯实基础】
1、下列表示一次函数y=2x+4的图象的是( )
2、如图,把直线沿x轴负方向向左平移4个单位,得到直线,则直线的解析式为 (???? )
A. ???? ? B. ??????
C.????? D.
3、函数y=3x6的图象经过的象限正确的是( )
A.第一、二、四象限 B.第二、三、四象限
C.第一、三、四象限 D.第一、二、三象限
4、直线与相交于点(4,5),且两直线与y轴围成的三角形的面积为16,那么b1b2的值为( )
A.8 B.16 C.32 D.无法确定
5、已知一次函数y=2kx(2k6)的图象经过原点,则函数的解析式是 .
6、如图直线y=mx+n过A(3,0)和点B(0,2),则关于x的方程mx+n=0的解为__ _______.
7、求下列函数与x轴和y轴的交点坐标,并在同一坐标系中画出它们的图象.
(1)①;
②;
(2)求两条直线与x轴所围成的△ABC的面积.
8、求下列一次函数的解析式:
(1)函数的图象经过点(2,4),且与直线3x+ y=5平行;
(2)函数图象和直线y=5x14在y轴上相交同一点,且过点(3,2);
(3)一次函数y=ax8的图象与x轴、y轴的交点之间的距离为10.
【提优特训】
9、在同一坐标系中,画出直线与的图象,其中正确的是( )
10、若一次函数y=kx+b的图象不经过第二象限,则点P(kb, kb)所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11、将直线y=ax+b向右平移3个单位,再向下平移4个单位,所得到的直线解析式为y=4x+3,则a、b的值为( )
A.a=4,b=3 B.a=4,b=3 C.a=4,b=5 D.a=4,b=5
12、已知一次函数的图象经过点A(3, 4)、点B(2,6)和点C(m,1)三点,则m的值为 .
13、如图所示,已知直线l1: 和直线l2: 相交于点A ,点A的横坐标为4,则关于x的不等式的解集为 .
14、甲、乙两位同学从学校出发到相距36km的植物园采集标本,骑自行车由同一条路前往,他们离出发地的距离s(km)和行驶时间t(h)之间的函数图象如图所示.根据图中提供的信息:有以下论断①乙同学比甲同学晚出发1(h);②乙同学出发1(h)追上甲同学;③甲同学的速度比乙同学的速度快;④乙同学到达目的地时,甲同学离目的地还有9km的路程. 符合图象描述的说法是 .(写出序号即可)
15、已知函数的图象不经过第一象限,且m为整数,则函数的解析式是 ,若此函数的图象与x轴、y轴分别交于A、B两点,则△AOB的面积为 ,把△AOB绕点A逆时针旋转90°后得到 ,则点的坐标是 .
16、已知一次函数y=3ax+9与y=2xb的图象都经过点A(2,3),且与x轴分别交于点B、C,求:
(1)求点B、C的坐标;
(2)求△ABC的面积.
17、如图,直线与x轴、y轴分别交于A、B两点,另一条直线经过点B,且与线段OA相交于点C,若直线将△AOB的面积分成1︰2的两部分,求直线的解析式.
18、如图,在平面直角坐标系中,点A的坐标为(2,5),点B的坐标为(4,3).请你在x轴上找一点P,使PA+PB的值最小.
(1)求点P的坐标;(2)求PA+PB的最小值.
【中考链接】
19.2018?甘肃定西16.(3分)如图,一次函数y=x2与y=2x+m的图象相交于点P(n,4),则关于x的不等式组的解集为 -2
A.y=2x4 B.y=2x+4 C.y=2x+2 D.y=2x2
21、2018?广西桂林12. 如图,在平面直角坐标系中,M、N、C三点的坐标分别为(,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A. B. C. D.
22、2018黑龙江龙东地区25.(8.00分)某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 20 吨,a= 15 .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
参考答案
1、B 2、C 3、B 4、A 5、, 6、 9、C 10、D 11、C 12、
13、 14、①、②、④ 15、、 、 19、
20、A 21、A
7、解:(1)①∵,
∴令x=0,y=6,则直线与y轴的交点坐标为(0,6).
∴令y=0,x=2,则直线与x轴的交点坐标为(2,0).
过点(2,0)和点(0,6)画出直线即可;
∵②,
∴令x=0,y=6.
则直线与y轴的交点坐标为(0, 6).
∴令y=0,x=4,
则直线与x轴的交点坐标为(4,0).
过点(4,0)和点(0, 6)画出直线即可;
所画的图象如图所示.
(3)∵直线和直线的相交于点A,
∴可得方程组,
∴解方程组,得,
∴点A的坐标为,点A到x轴的距离为2.
∵点B的坐标为(2,0)、点C的坐标为(4,0),
∴BC=42=2,
∴△ABC的面积=.
8、解:(1)设所求一次函数的解析式为y1=kx+b,
∵3x+ y=5,
∴y=3x+5.
∵y1∥y,
∴k=3.
∴y1=3x+b.
把点(2,4)代入y1=3x+b得,
4=3×(2)+b,
解得b=10.
∴所求一次函数的解析式为y1=3x10.
(2)令x=0, y=14,
∴直线y=5x14与y轴的交点坐标(0, 14).
∵所求直线与直线y=5x14在y轴上相交同一点,
∴设所求直线的解析式为y=kx14.
把点(3,2)代入y=kx14得,
2=3k14,
解得k =4.
∴所求一次函数的解析式为y=4x14.
(3)根据题意,得a≠0, 且一次函数y=ax8的图象与x轴、y轴的交点坐标分别为
、(0,8),
由勾股定理,得,
解得,
∴所求一次函数的解析式为.
16、解:(1)把点A(2,3)分别代入一次函数y=3ax+9与y=2xb中,
3=3×(2)a+9,3=2×(2)b,
解得a=2,b=7.
所以一次函数解析式分别为y=6x+9、y=2x7.
令y=0,则6x+9=0、2x7=0,
解得、.
所以点B的坐标为,点C的坐标为.
(2) ∵直线y=6x+9与y=2x7相交于A(2,3),
∴点A的x轴的距离为.
∵点B的坐标为,点C的坐标为,
∴.
∴△ABC的面积=.
17、解:如图①∵直线与x轴、y轴分别交于A、B两点,
∴令x=0,y=2,则点B的坐标为(0,2).
∴令y=0,x=12,则点A的坐标为(12,0).
直线将△AOB的面积分成1︰2的两部分,
(1)如图②S△ABC=2 S△CBO,
∵△ABC与△CBO是同高的三角形,
∴AC=2OC.
∴OC+2OC=OA=12,
∴OC=4.
∴点C的坐标为(4,0).
将点B(0,2)和点C(4,0)分别代入得,
,解得,.
∴函数的解析式为;
(2)如图③S△CBO =2 S△ABC,
∵△ABC与△CBO是同高的三角形,
∴OC =2 AC.
∴,
∴OC=8.
∴点C的坐标为(8,0).
将点B(0,2)和点C(8,0)分别代入得,
, 解得,.
∴函数的解析式为.
∴直线的解析式为或.
18、解如图,(1)①作出点A关于x轴的对称点A′(2,5),点D是垂足,
②连结A′B,交x轴于点P,点P就是要求的点.
③设直线A′B的解析式为y=kx+b,
把点A′(2,5)、点B(4,3)代入y=kx+b,
得,解得,.
∴直线A′B的解析式为.
令y=0,则,
解得,,
∴点P的坐标为.
(2)过B作BC⊥x轴,点C是垂足,过A′作A′E⊥y轴,点E是垂足,
延长BC、A′E相交于点Q,则Q的坐标为(4,5).由对称性可知AP=A′P,PAPB= PA′PB=A′B;
∴A′B最短,(两点之间,线段最短),即AP+PB最小,
∴在Rt△A′QB中,A′Q=6,QB=8,
∴
即PA+PB的最小值为10.
也可利用两点之间的距离公式求
将点B(4,3),点A′(2,5)代入公式,
.
21、【答案】A
【解析】分析:分别求出当点A与点M、N重合时直线AC的解析式,由AB⊥AC可得直线AB的解析式,从而求出b的值,最终可确定b的取值范围.
【解答】:当点A与点N重合时,MN⊥AC,
∴MN是直线AB的一部分,
∵N(3,1)
∴此时b=1;
当点A与点M重合时,设直线AC的解析式为y=k1x+m,
由于AC经过点A、C两点,故可得,解得:,
设直线AB的解析式为y=k2x+b,
∵AB⊥AC,
∴,
∴.
故直线AB的解析式为y=x+b,
把(,1)代入y=x+b得, b=.
∴b的取值范围是.
故选A.
点睛:此题考查一次函数基本性质,待定系数求解析式,简单的几何关系.
22、【分析】(1)根据题意,由图2得出两个车间同时加工和甲单独加工的速度;
(2)用待定系数法解决问题;
(3)求出两个车间每天加工速度分别计算两个55吨完成的时间.
【解答】解:(1)由图象可知,第一天甲乙共加工220185=35吨,第二天,乙停止工作,甲单独加工185165=20吨,
则乙一天加工3520=15吨.a=15
故答案为:20,15
(2)设y=kx+b
把(2,15),(5,120)代入
,解得,,
∴y=35x55.
(3)由图2可知
当w=220﹣55=165时,恰好是第二天加工结束.
当2≤x≤5时,两个车间每天加工速度为=55吨
∴再过1天装满第二节车厢
【点评】本题为一次函数实际应用问题,应用了待定系数法.解答要注意通过对边两个函数图象实际意义对比分析得到问题答案.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
