5.4 一次函数的图象(2)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 5.4 一次函数的图象(2)(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 389.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 10:28:13 | ||
图片预览




文档简介
浙江版八年级数学上册第5章5.4一次函数图象
第2课时 一次函数图象(2)
【知识清单】
一、正比例函数和一次函数及性质
正比例函数
一次函数
概 念
一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.
一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,是y=kx,所以说正比例函数是一种特殊的一次函数.
自变量
范 围
x为全体实数
图 象
一条直线
必过点
(0,0)、(1,k)
(0,b)和(,0)
走 向
k>0时,直线经过一、三象限;
k<0时,直线经过二、四象限.
k>0,b>0,直线经过第一、二、三象限
k>0,b<0,直线经过第一、三、四象限
k<0,b>0,直线经过第一、二、四象限
k<0,b<0,直线经过第二、三、四象限
增减性
k>0,y随x的增大而增大;(从左向右上升)
k<0,y随x的增大而减小.(从左向右下降)
倾斜度
越大,越接近y轴;越小,越接近x轴.
图像的
平 移
左右平移:左右平移的规律:左加右减 .
图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小.
上下平移:上下平移的规律:上加下减 .
b>0时,将直线y=kx的图象向上平移个单位;
b<0时,将直线y=kx的图象向下平移个单位.
二、象限角平分线的解析式:
一、三象限角平分线是直线y=x,二、四象限角平分线是直线y=x.
三、实际问题情境中的图像的画法:
实际问题情境中的图像必须在自变量的取值范围内画出.
【经典例题】
例题1、已知点A1(x1,y1)、A2(x2,y2)、A3(x3,y3)在直线y=5x6上,且x1则y1,y2,y3的大小关系是是( ).
A.y1 【考点】一次函数的性质及一次函数图象上点的坐标特征.
【分析】由一次函数y=5x6可知,k=5<0,y随x的增大而减小..
【解答】由y=5x6可知,k=5<0,y随x的增大而减小,
又∵x1∴y1>y2>y3.故选C.
【点评】本题考查的是一次函数的性质,熟知一次函数y=kx+b(k≠0)中,当k<0时,y随x的增大而减小是解答此题的关键.
例题2、已知一次函数y=(3a+12)x(82b),求字母a,b取何值时:
(1)y随x的增大而减小;
(2)图像经过原点;
(3)图像平行于直线y=6x+5,且与直线y=3x4在y轴上相交于同一点;
(4)图像与y轴交点在y轴的负半轴上.
【考点】一次函数图象与系数的关系,一次函数y=kx+b中,k、b的值决定图象的位置,反之亦然.
【分析】(1)y随x的增大而减小,则3a+12<0;
(2) 图像经过原点,则3a+12≠0,(82b)=0;
(3)根据题意,得 3a+12=3. (82b)=4
(4)图像与y轴交点在y轴的负半轴上,则3a+12≠0,(82b)<0.
【解答】(1)y随x的增大而减小,
则3a+12<0,
所以a<4,b取任意实数.
(2) 图像经过原点,则3a+12≠0,(82b)=0;
所以a≠4,b=4.
(3)根据题意,得 3a+12=-3, (82b)=-4,
解得a=-5,b=2.
(4)图像与y轴交点在y轴的负半轴上,
则3a+12≠0, (82b)<0.
解得a≠4,b<4.
【点评】本题需注意应根据所给条件分别判断x的系数和常数项的符号,进而判断未知字母的值.
【夯实基础】
1、在下列一次函数中,y随x的增大而增大的是( )
A. ???? B. ??? ??C.????? D.
2、若一次函数y=axb满足ab>0且y随x的减小而增大,则它的大致图象是下列图中的(???? )
3、已知一次函数y=3x+2m与y=3x+2n的图象都经过(a,6),则(m+n+5)2019的值是( )
A.72019 B.72019 C.1 D.1
4、某市为了节约用水,按以下规定收取水费:(1)每户每月用水量不超过30 m3,则每立方米水费1.5元;(2)每户每月用水量超过30 m3,则超过的部分每立方米水费2.2元,下面可以刻画出该户交纳水费随用水量的变化情况大致图象为(? ???)?
5、已知点(a1,5a),在一次函数y=2x7的图象上,则函数y=(a1)x+5a的解析式是 .
6、若一次函数的解析式为,则y随x的增大而 增大 .
7、在平面直角坐标系中,点A的坐标为(2,0),直线l是一、三象限角平分线,点P是l上的一点,使△POA是等腰三角形,求所有满足条件的点P的坐标.
8、 某工厂生产甲、乙两种产品的相关信息如下表,
价目
品种
出厂价
成本价
排污处理费
甲种产品
1600(元/吨)
550(元/吨)
160(元/吨)
乙种产品
1900(元/吨)
850(元/吨)
80(元/吨)每月还需支付设备管理、养护费16000元
请你解答下列问题:
(1)设工厂每月生产甲、乙两种产品各x吨,利润分别为y1元和y2元,分别求y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该工厂每月生产甲、乙两种产品均不超过300吨,若某月要生产甲、乙两种产品共500吨,求该月生产甲、乙产品各多少吨,获得的总利润最大?最大 利润是多少?
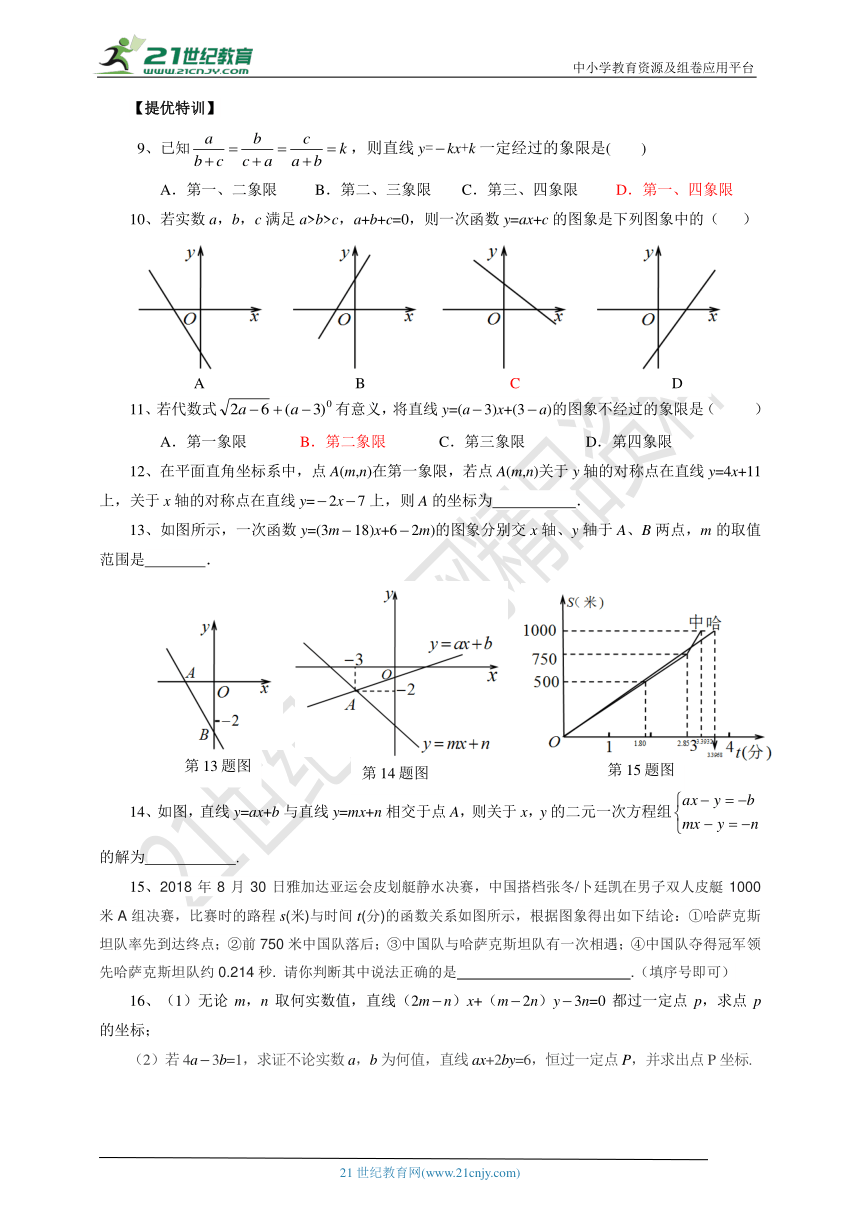
【提优特训】
9、已知,则直线y=kx+k一定经过的象限是( )
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
10、若实数a,b,c满足a>b>c,a+b+c=0,则一次函数y=ax+c的图象是下列图象中的( )
11、若代数式有意义,将直线y=(a3)x+(3a)的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12、在平面直角坐标系中,点A(m,n)在第一象限,若点A(m,n)关于y轴的对称点在直线y=4x+11上,关于x轴的对称点在直线y=2x7上,则A的坐标为 .
13、如图所示,一次函数y=(3m18)x+62m)的图象分别交x轴、y轴于A、B两点,m的取值范围是 .
14、如图,直线y=ax+b与直线y=mx+n相交于点A,则关于x,y的二元一次方程组的解为 .
15、2018年8月30日雅加达亚运会皮划艇静水决赛,中国搭档张冬/卜廷凯在男子双人皮艇1000米A组决赛,比赛时的路程s(米)与时间t(分)的函数关系如图所示,根据图象得出如下结论:①哈萨克斯坦队率先到达终点;②前750米中国队落后;③中国队与哈萨克斯坦队有一次相遇;④中国队夺得冠军领先哈萨克斯坦队约0.214秒. 请你判断其中说法正确的是 .(填序号即可)
16、(1)无论m,n取何实数值,直线(2mn)x+(m2n)y3n=0都过一定点p,求点p的坐标;
(2)若4a3b=1,求证不论实数a,b为何值,直线ax+2by=6,恒过一定点P,并求出点P坐标.
17、如图,在平面直角坐标系中,直线l:y=kx+b的图象经过点A(2,4),且与x轴相交于点B;直线l1:y=mx+n的图象经过D、E两点,OE=1,∠EDB=45°,l与l1相交于点C,点C的横坐标为1.
(1)求l、l1的解析式;
(2)若点P在y轴上,且满足S△COP=S△DCB,求点P的坐标.
18、先阅读下列材料,再解决问题:
如图,已知点和直线:Ax+By+C=0(设),求点P到直线的距离.
先进行公式推导:
∵,
∴这时直线与x轴,y轴都相交,
过点P作x轴的平行线,交于点;作y轴的平行线,交于点;作PD⊥直线,垂足为D,设PD=d.
把点,点分别代入直线:Ax+By+C=0得,
Ax1+By0+C=0,Ax0+By2+C=0
解得,,.
∴,.
在Rt△APB中,
.
由三角形的面积公式可得,.
∴
∴
例题1求点P(2,5)到直线y=2x-3的距离;
2、求两直线3x+4y-2=0与6x+8y-5=0的距离.
解:1将直线y=2x-3,化成Ax+By+C=0的形式为2x-y-3=0,
则A=2,B=-1,C=-3,
所以
2∵直线3x+4y2=0,可化成,
直线6x+8y5=0,可化成.
∴直线3x+4y2=0与直线6x+8y5=0平行.
∴在直线3x+4y-2=0任取一点到直线6x+8y-5=0的距离,就是两条直线的距离,
当,,点,A=6,B=8,C=-5,
则
两直线3x+4y2=0与6x+8y5=0的距离为.
根据以上材料,解决下列问题:
1.求点P(-2,-3)到直线的距离;
2.若点P(1,0)到直线x+y+c=0的距离为,求实数c的值.
【中考链接】
19.2018湖南省湘潭7.(3分)若b>0,则一次函数y=x+b的图象大致是( )
20、2018湖南常德4.(3分)若一次函数y=(k2)x+1的函数值y随x的增大而增大,则( )
A.k<2 B.k>2 C.k>0 D.k<0
21、2018山东滨州12.(3分)如果规定[x]表示不大于x的最大整数,例如[2.3]=2,那么函数y=x [x]的图象为( )
22、2018?十堰15.(3.00分)如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式x(kx+b)<0的解集为 .
参考答案
1、A 2、C 3、D 4、C 5、, 6、增大 9、D 10、C 11、B 12、
13、 14、 15、②、③、④、 19、C 20、B 21、A 22、
7、解:∵直线l是一、三象限角平分线,
∴直线l的解析式为y=x.
①在直线y=x上作OP=OA=2,可得符合条件的P1、P2两点,
点P1的坐标为,点P2的坐标为;
②过点A作l的垂线,垂足为P3,
∵∠P3OA=45°,∠OP3A=90°,
∴OP3=P3A,点P3的坐标为;
③过点A作x轴的垂线交l于点P4,
与②同理OA=P4A,点P4的坐标为
8、解:(1)由表中信息知:y1=(1600550160)x =890x,
y2=(190085080)x16000,
即y2=970x16000;
(2)设该月生产甲种产品x吨,则生产乙种产品(500x)吨,
y=890x+970(500x)16000
=80x+469000,
∵
∴200≤x≤300,
∵k=80<0,
所以y随x的增大而减小,
故当x=200时,获得利润最大,最大利润为:
y=80×200+469000=453000.
16、解:(1)∵(2mn)x+(m2n)y3n=0,
?(2x+y)m +(x2y3)n =0,
我们要寻找点P (x,y),无论m,n取何值上式恒成立.
显然当2x+y=0和x2y1=0时满足要求.
∴,解得
∴点P坐标为(1, 2)
(2)∵4a3b=1,
∴ax+2by=6(4a3b)
ax+2by=24a18b
(x24) a +2b(y+9)=0
当x=10,y=9时,
a、b有无数解.
∴无论为何值,直线ax+2by=6恒过点(24, 9).
17、解:(1)在Rt△DOE中,
∵∠EDB=45°,OE=1,∴OD=1.
∴点D、E的坐标分别为(0,1)、(1,0),
∴,解得
∴直线l1的解析式为y=x+1
当x=1时,y=x+1=2,
∴点C的坐标为(1,2).
将A(2,4)、C(1,2)代入y=kx+b,
得: ,解得.
∴直线l的解析式为.
令y=0, ,解得.
∴点B的坐标为(4,0).
(2)∵点B坐标为(4,0),点D坐标为(1,0),
∴BD=4(1)=5
设点P的坐标为(0,m),OP=.
∵S△COP=S△DCB,即,
解得:,
∴点P的坐标为或.
18、解:1.∵P(2,3),A=3,B=4,C=2,
∴
2.,
∴,
∴c+1=±2,
∴c1=3,c2=1.
19、【分析】根据一次函数的k、b的符号确定其经过的象限即可确定答案.
【解答】解:∵一次函数y=x+b中k=1<0,b>0,
∴一次函数的图象经过一、二、四象限,
故选:C.
【点评】主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
20、【分析】根据一次函数的性质,可得答案.
【解答】解:由题意,得
k2>0,
解得k>2,
故选:B.
【点评】本题考查了一次函数的性质,y=kx+b,当k>0时,函数值y随x的增大而增大.
21、【分析】根据定义可将函数进行化简.
【解答】解:当1≤x<0,[x]= 1,y=x+1
当0≤x<1时,[x]=0,y=x
当1≤x<2时,[x]=1,y=x1
……
故选:A.
【点评】本题考查函数的图象,解题的关键是正确理解[x]的定义,然后对函数进行化简,本题属于中等题型.
22、【考点】FD:一次函数与一元一次不等式.
【专题】31 :数形结合.
【分析】先把不等式x(kx+b)<0化为或,
然后利用函数图象分别解两个不等式组.
【解答】解:不等式x(kx+b)<0化为或,
利用函数图象得为无解,的解集为﹣3<x<0,
所以不等式x(kx+b)<0的解集为3<x<0.
故答案为3<x<0.
【点评】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
第2课时 一次函数图象(2)
【知识清单】
一、正比例函数和一次函数及性质
正比例函数
一次函数
概 念
一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.
一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,是y=kx,所以说正比例函数是一种特殊的一次函数.
自变量
范 围
x为全体实数
图 象
一条直线
必过点
(0,0)、(1,k)
(0,b)和(,0)
走 向
k>0时,直线经过一、三象限;
k<0时,直线经过二、四象限.
k>0,b>0,直线经过第一、二、三象限
k>0,b<0,直线经过第一、三、四象限
k<0,b>0,直线经过第一、二、四象限
k<0,b<0,直线经过第二、三、四象限
增减性
k>0,y随x的增大而增大;(从左向右上升)
k<0,y随x的增大而减小.(从左向右下降)
倾斜度
越大,越接近y轴;越小,越接近x轴.
图像的
平 移
左右平移:左右平移的规律:左加右减 .
图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小.
上下平移:上下平移的规律:上加下减 .
b>0时,将直线y=kx的图象向上平移个单位;
b<0时,将直线y=kx的图象向下平移个单位.
二、象限角平分线的解析式:
一、三象限角平分线是直线y=x,二、四象限角平分线是直线y=x.
三、实际问题情境中的图像的画法:
实际问题情境中的图像必须在自变量的取值范围内画出.
【经典例题】
例题1、已知点A1(x1,y1)、A2(x2,y2)、A3(x3,y3)在直线y=5x6上,且x1
A.y1
【分析】由一次函数y=5x6可知,k=5<0,y随x的增大而减小..
【解答】由y=5x6可知,k=5<0,y随x的增大而减小,
又∵x1
【点评】本题考查的是一次函数的性质,熟知一次函数y=kx+b(k≠0)中,当k<0时,y随x的增大而减小是解答此题的关键.
例题2、已知一次函数y=(3a+12)x(82b),求字母a,b取何值时:
(1)y随x的增大而减小;
(2)图像经过原点;
(3)图像平行于直线y=6x+5,且与直线y=3x4在y轴上相交于同一点;
(4)图像与y轴交点在y轴的负半轴上.
【考点】一次函数图象与系数的关系,一次函数y=kx+b中,k、b的值决定图象的位置,反之亦然.
【分析】(1)y随x的增大而减小,则3a+12<0;
(2) 图像经过原点,则3a+12≠0,(82b)=0;
(3)根据题意,得 3a+12=3. (82b)=4
(4)图像与y轴交点在y轴的负半轴上,则3a+12≠0,(82b)<0.
【解答】(1)y随x的增大而减小,
则3a+12<0,
所以a<4,b取任意实数.
(2) 图像经过原点,则3a+12≠0,(82b)=0;
所以a≠4,b=4.
(3)根据题意,得 3a+12=-3, (82b)=-4,
解得a=-5,b=2.
(4)图像与y轴交点在y轴的负半轴上,
则3a+12≠0, (82b)<0.
解得a≠4,b<4.
【点评】本题需注意应根据所给条件分别判断x的系数和常数项的符号,进而判断未知字母的值.
【夯实基础】
1、在下列一次函数中,y随x的增大而增大的是( )
A. ???? B. ??? ??C.????? D.
2、若一次函数y=axb满足ab>0且y随x的减小而增大,则它的大致图象是下列图中的(???? )
3、已知一次函数y=3x+2m与y=3x+2n的图象都经过(a,6),则(m+n+5)2019的值是( )
A.72019 B.72019 C.1 D.1
4、某市为了节约用水,按以下规定收取水费:(1)每户每月用水量不超过30 m3,则每立方米水费1.5元;(2)每户每月用水量超过30 m3,则超过的部分每立方米水费2.2元,下面可以刻画出该户交纳水费随用水量的变化情况大致图象为(? ???)?
5、已知点(a1,5a),在一次函数y=2x7的图象上,则函数y=(a1)x+5a的解析式是 .
6、若一次函数的解析式为,则y随x的增大而 增大 .
7、在平面直角坐标系中,点A的坐标为(2,0),直线l是一、三象限角平分线,点P是l上的一点,使△POA是等腰三角形,求所有满足条件的点P的坐标.
8、 某工厂生产甲、乙两种产品的相关信息如下表,
价目
品种
出厂价
成本价
排污处理费
甲种产品
1600(元/吨)
550(元/吨)
160(元/吨)
乙种产品
1900(元/吨)
850(元/吨)
80(元/吨)每月还需支付设备管理、养护费16000元
请你解答下列问题:
(1)设工厂每月生产甲、乙两种产品各x吨,利润分别为y1元和y2元,分别求y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该工厂每月生产甲、乙两种产品均不超过300吨,若某月要生产甲、乙两种产品共500吨,求该月生产甲、乙产品各多少吨,获得的总利润最大?最大 利润是多少?
【提优特训】
9、已知,则直线y=kx+k一定经过的象限是( )
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
10、若实数a,b,c满足a>b>c,a+b+c=0,则一次函数y=ax+c的图象是下列图象中的( )
11、若代数式有意义,将直线y=(a3)x+(3a)的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12、在平面直角坐标系中,点A(m,n)在第一象限,若点A(m,n)关于y轴的对称点在直线y=4x+11上,关于x轴的对称点在直线y=2x7上,则A的坐标为 .
13、如图所示,一次函数y=(3m18)x+62m)的图象分别交x轴、y轴于A、B两点,m的取值范围是 .
14、如图,直线y=ax+b与直线y=mx+n相交于点A,则关于x,y的二元一次方程组的解为 .
15、2018年8月30日雅加达亚运会皮划艇静水决赛,中国搭档张冬/卜廷凯在男子双人皮艇1000米A组决赛,比赛时的路程s(米)与时间t(分)的函数关系如图所示,根据图象得出如下结论:①哈萨克斯坦队率先到达终点;②前750米中国队落后;③中国队与哈萨克斯坦队有一次相遇;④中国队夺得冠军领先哈萨克斯坦队约0.214秒. 请你判断其中说法正确的是 .(填序号即可)
16、(1)无论m,n取何实数值,直线(2mn)x+(m2n)y3n=0都过一定点p,求点p的坐标;
(2)若4a3b=1,求证不论实数a,b为何值,直线ax+2by=6,恒过一定点P,并求出点P坐标.
17、如图,在平面直角坐标系中,直线l:y=kx+b的图象经过点A(2,4),且与x轴相交于点B;直线l1:y=mx+n的图象经过D、E两点,OE=1,∠EDB=45°,l与l1相交于点C,点C的横坐标为1.
(1)求l、l1的解析式;
(2)若点P在y轴上,且满足S△COP=S△DCB,求点P的坐标.
18、先阅读下列材料,再解决问题:
如图,已知点和直线:Ax+By+C=0(设),求点P到直线的距离.
先进行公式推导:
∵,
∴这时直线与x轴,y轴都相交,
过点P作x轴的平行线,交于点;作y轴的平行线,交于点;作PD⊥直线,垂足为D,设PD=d.
把点,点分别代入直线:Ax+By+C=0得,
Ax1+By0+C=0,Ax0+By2+C=0
解得,,.
∴,.
在Rt△APB中,
.
由三角形的面积公式可得,.
∴
∴
例题1求点P(2,5)到直线y=2x-3的距离;
2、求两直线3x+4y-2=0与6x+8y-5=0的距离.
解:1将直线y=2x-3,化成Ax+By+C=0的形式为2x-y-3=0,
则A=2,B=-1,C=-3,
所以
2∵直线3x+4y2=0,可化成,
直线6x+8y5=0,可化成.
∴直线3x+4y2=0与直线6x+8y5=0平行.
∴在直线3x+4y-2=0任取一点到直线6x+8y-5=0的距离,就是两条直线的距离,
当,,点,A=6,B=8,C=-5,
则
两直线3x+4y2=0与6x+8y5=0的距离为.
根据以上材料,解决下列问题:
1.求点P(-2,-3)到直线的距离;
2.若点P(1,0)到直线x+y+c=0的距离为,求实数c的值.
【中考链接】
19.2018湖南省湘潭7.(3分)若b>0,则一次函数y=x+b的图象大致是( )
20、2018湖南常德4.(3分)若一次函数y=(k2)x+1的函数值y随x的增大而增大,则( )
A.k<2 B.k>2 C.k>0 D.k<0
21、2018山东滨州12.(3分)如果规定[x]表示不大于x的最大整数,例如[2.3]=2,那么函数y=x [x]的图象为( )
22、2018?十堰15.(3.00分)如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式x(kx+b)<0的解集为 .
参考答案
1、A 2、C 3、D 4、C 5、, 6、增大 9、D 10、C 11、B 12、
13、 14、 15、②、③、④、 19、C 20、B 21、A 22、
7、解:∵直线l是一、三象限角平分线,
∴直线l的解析式为y=x.
①在直线y=x上作OP=OA=2,可得符合条件的P1、P2两点,
点P1的坐标为,点P2的坐标为;
②过点A作l的垂线,垂足为P3,
∵∠P3OA=45°,∠OP3A=90°,
∴OP3=P3A,点P3的坐标为;
③过点A作x轴的垂线交l于点P4,
与②同理OA=P4A,点P4的坐标为
8、解:(1)由表中信息知:y1=(1600550160)x =890x,
y2=(190085080)x16000,
即y2=970x16000;
(2)设该月生产甲种产品x吨,则生产乙种产品(500x)吨,
y=890x+970(500x)16000
=80x+469000,
∵
∴200≤x≤300,
∵k=80<0,
所以y随x的增大而减小,
故当x=200时,获得利润最大,最大利润为:
y=80×200+469000=453000.
16、解:(1)∵(2mn)x+(m2n)y3n=0,
?(2x+y)m +(x2y3)n =0,
我们要寻找点P (x,y),无论m,n取何值上式恒成立.
显然当2x+y=0和x2y1=0时满足要求.
∴,解得
∴点P坐标为(1, 2)
(2)∵4a3b=1,
∴ax+2by=6(4a3b)
ax+2by=24a18b
(x24) a +2b(y+9)=0
当x=10,y=9时,
a、b有无数解.
∴无论为何值,直线ax+2by=6恒过点(24, 9).
17、解:(1)在Rt△DOE中,
∵∠EDB=45°,OE=1,∴OD=1.
∴点D、E的坐标分别为(0,1)、(1,0),
∴,解得
∴直线l1的解析式为y=x+1
当x=1时,y=x+1=2,
∴点C的坐标为(1,2).
将A(2,4)、C(1,2)代入y=kx+b,
得: ,解得.
∴直线l的解析式为.
令y=0, ,解得.
∴点B的坐标为(4,0).
(2)∵点B坐标为(4,0),点D坐标为(1,0),
∴BD=4(1)=5
设点P的坐标为(0,m),OP=.
∵S△COP=S△DCB,即,
解得:,
∴点P的坐标为或.
18、解:1.∵P(2,3),A=3,B=4,C=2,
∴
2.,
∴,
∴c+1=±2,
∴c1=3,c2=1.
19、【分析】根据一次函数的k、b的符号确定其经过的象限即可确定答案.
【解答】解:∵一次函数y=x+b中k=1<0,b>0,
∴一次函数的图象经过一、二、四象限,
故选:C.
【点评】主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
20、【分析】根据一次函数的性质,可得答案.
【解答】解:由题意,得
k2>0,
解得k>2,
故选:B.
【点评】本题考查了一次函数的性质,y=kx+b,当k>0时,函数值y随x的增大而增大.
21、【分析】根据定义可将函数进行化简.
【解答】解:当1≤x<0,[x]= 1,y=x+1
当0≤x<1时,[x]=0,y=x
当1≤x<2时,[x]=1,y=x1
……
故选:A.
【点评】本题考查函数的图象,解题的关键是正确理解[x]的定义,然后对函数进行化简,本题属于中等题型.
22、【考点】FD:一次函数与一元一次不等式.
【专题】31 :数形结合.
【分析】先把不等式x(kx+b)<0化为或,
然后利用函数图象分别解两个不等式组.
【解答】解:不等式x(kx+b)<0化为或,
利用函数图象得为无解,的解集为﹣3<x<0,
所以不等式x(kx+b)<0的解集为3<x<0.
故答案为3<x<0.
【点评】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
