第二章 有理数的运算好题精选（含解析）

绝密★启用前
期末复习第二章有理数的运算好题精选
题号
一
二
三
总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
　
第Ⅰ卷（选择题）
请点击修改第I卷的文字说明
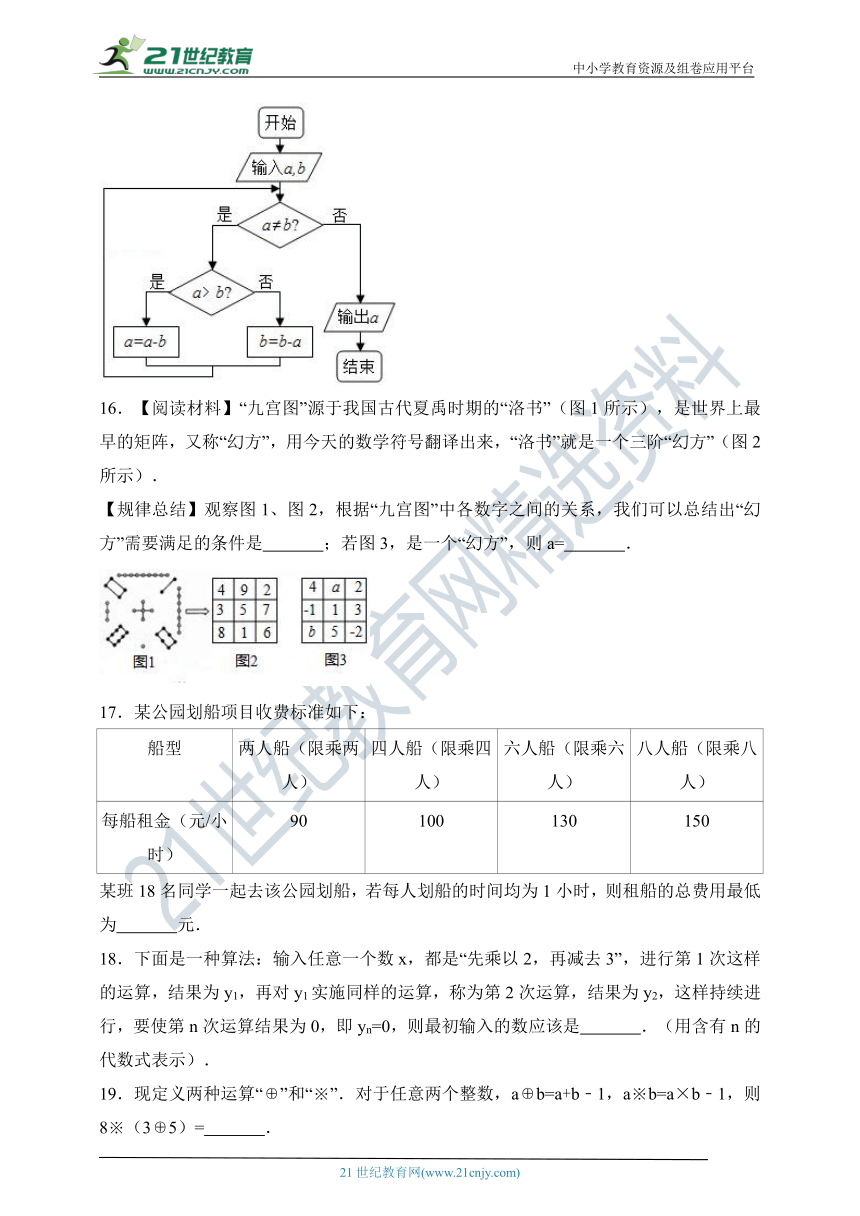
评卷人
得 分


一．选择题（共10小题）
1．在数学课上，老师让甲、乙、丙、丁，四位同学分别做了一道有理数运算题，你认为做对的同学是（　　）
甲：9﹣32÷8=0÷8=0
乙：24﹣（4×32）=24﹣4×6=0
丙：（36﹣12）÷=36×﹣12×=16
丁：（﹣3）2÷×3=9÷1=9
A．甲 B．乙 C．丙 D．丁
2．十进制数278，记作278（10），其实278（10）=2×102+7×101+8×100，二进制数101（2）=1×22+0×21+1×20．有一个k（0＜k≤10为整数）进制数165（k），把它的三个数字顺序颠倒得到的k进制数561（k）是原数的3倍，则k=（　　）
A．10 B．9 C．8 D．7
3．规定★为：x★y=+．已知2★1=．则15★16的值为（　　）
A． B．﹣ C． D．或﹣
4．已知|a+2|+（b+3）2=0，则下列式子的值最小是（　　）
A．a+b B．ab C．ba D．a﹣b
5．如图，现有3×3的方格，每个小方格内均有不同的数字，要求方格内每一行．每一列以及每一条对角线上的三个数字之和均相等，图中给出了部分数字，则P处对应的数字是（　　）
A．7 B．5 C．4 D．1
6．规定：求若干个相同的有理数（均不等）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”一般地，把（a≠0）记作a，读作“a的圈n次方”．关于除方，下列说法错误的是（　　）
A．任何非零数的圈2次方都等于1
B．对于任何正整数n，1=1
C．3④=4③
D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数
7．取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．经过下面5步运算可得1，即：如图所示．如果自然数m恰好经过7步运算可得到1，则所有符合条件的m的值有（　　）
A．3个 B．4个 C．5个 D．6个
8．定义一种关于整数n的“F”运算：
（1）当n是奇数时，结果为3n+5；
（2）当n是偶数时，结果是（其中k是使是奇数的正整数），并且运算重复进行．
例如：取n=58，第一次经F运算是29，第二次经F运算是92，第三次经F运算是23，第四次经F运算是74…；若n=9，则第2017次运算结果是（　　）
A．1 B．2 C．7 D．8
9．如图，在一个由6个圆圈组成的三角形里，把1到6这6个数分别填入图的圆圈中，要求三角形的每条边上的三个数的和S都相等，那么S的最大值是（　　）
?
A．9 B．10 C．12 D．13
10．计算机中常用的16进制是逢16进1的计算制，采用数字0﹣9和字母A﹣F共16个计数符号，这些符号与十进制的数对应关系如下表．
16进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如，用十六进制表示：E+D=1B，则A×B=（　　）
A．6E B．72 C．5F D．B0
　

第Ⅱ卷（非选择题）
请点击修改第Ⅱ卷的文字说明
评卷人
得 分


二．填空题（共15小题）
11．设x为非负实数，将x“四舍五入”到整数的值记为＜x＞（可读作尖括号x），即当非负实数x满足n﹣≤x＜n+时，其中n为整数，则＜x＞=n．如＜0.48＞=0，＜5.5＞=6，＜3.49＞=3．如果＜x﹣2.2＞=5，那么x的取值范围是　 　
12．一般的，如果ax=N（a＞0，且a≠1），那么x叫做以a为底N的对数，记作x=logaN．例如：由于23=8，所以3是以2为底8的对数，记作log28=3；由于a1=a，所以1是以a为底a的对数，记作logaa=1．
对数作为一种运算，有如下的运算性质：如果a＞0，且a≠1，M＞0，N＞0，那么：
（1）loga（M?N）=logaM+logaN；
（2）loga=logaM﹣logaN；
（3）logaMn=nlogaM．
根据上面的运算性质，计算log2（47×25）+log26﹣log23的结果是　 　．
13．定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为（其中k是使为奇数的正整数），并且重复运算，如取n=26，则
则当n=898时，第2018次“F”运算的结果是　 　．
14．已知a是不等于﹣1的数，我们把称为a的和倒数．如：2的和倒数为=，已知a1=1，a2是a1的和倒数，a3是a2的和倒数．a4是a3的和倒数，…，依此类推，则a1?a2?a3…a10=　 　．
15．如图，程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行程序框图，如果输入a，b的值分别为3，9，那么输出a的值为　 　．
16．【阅读材料】“九宫图”源于我国古代夏禹时期的“洛书”（图1所示），是世界上最早的矩阵，又称“幻方”，用今天的数学符号翻译出来，“洛书”就是一个三阶“幻方”（图2所示）．
【规律总结】观察图1、图2，根据“九宫图”中各数字之间的关系，我们可以总结出“幻方”需要满足的条件是　 　；若图3，是一个“幻方”，则a=　 　．
17．某公园划船项目收费标准如下：
船型
两人船（限乘两人）
四人船（限乘四人）
六人船（限乘六人）
八人船（限乘八人）
每船租金（元/小时）
90
100
130
150
某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为　 　元．
18．下面是一种算法：输入任意一个数x，都是“先乘以2，再减去3”，进行第1次这样的运算，结果为y1，再对y1实施同样的运算，称为第2次运算，结果为y2，这样持续进行，要使第n次运算结果为0，即yn=0，则最初输入的数应该是　 　．（用含有n的代数式表示）．
19．现定义两种运算“⊕”和“※”．对于任意两个整数，a⊕b=a+b﹣1，a※b=a×b﹣1，则8※（3⊕5）=　 　．
20．已知：C==3，C==10，C==15，…，观察上面的计算过程，寻找规律并计算：C=　 　．
21．在图（1）中，对任意相邻的上下或左右两格中的数字同时加1或减2，这算作一次操作，经过若干次操作后，图（1）能变为图（2），则图（2）中A格内的数是　 　
22．将一张长方形的纸按如图对折，对折时每次折痕与上次的折痕保持平行，第一次对折后可得到1条折痕（图中虚线），第二次对折后可得到3条折痕，第三次对折后得到7条折痕，那么第10次对折后得到的折痕比第9次对折后得到的折痕多　 　条．
23．将一张厚度均匀的纸反复对折，对折3次后，折成的纸的厚度为10mm，如果要使折成的厚度为40mm，那么对折的次数为　 　次．
24．观察下列等式：=×（1﹣），=×（﹣），=×（﹣），=×（﹣），…
根据你得出的规律写出第n个等式为　 　，并根据该规律计算：+++…+=　 　．
25．某种细胞开始有两个，1小时后分裂成4个并死去一个，2个小时后分裂成6个并死去一个，3小时后分裂成10个并死去1个，按此规律，请你计算经过n个小时后，细胞存活的个数为　 　个（结果用含n的代数式表示）
　
评卷人
得 分


三．解答题（共15小题）
26．计算：
（1）（+25）﹣（﹣10）
（2）（﹣）+（+）
（3）12﹣（﹣18）+（﹣7）﹣15+（﹣18）
（4）﹣42×（﹣）3+（﹣3）2÷（﹣）2
27．已知x，y为有理数，现规定一种新运算*，满足x*y=xy﹣2x+1
（1）求3*2的值；
（2）对于任意两个有理数x，y，是否都有x*y=y*x成立？如果成立，请证明，如果不成立，请举反例说明；
（3）如图，数轴上线段AB=2（单位长度），CD=4（单位长度），点A在数轴上表示的数是1*（﹣9），点C在数轴上表示的数是（﹣8）*．若线段AB以6个单位长度每秒的速度向右匀速运动，同时线段CD以2个单位长度每秒的速度向左匀速运动．问运动多少秒时，BC=8（单位长度）？此时点B在数轴上表示的数是多少．
28．有依次排列的3个数：3，9，8，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，﹣1，8，这称为第一次操作；第二次同样的操作后也可产生一个新数串：3，3，6，3，9，﹣10，﹣1，9，8；继续依次操作下去．问
（1）第一次操作后，增加的所有新数之和是多少？
（2）第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和是多少？
（3）猜想：第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和是多少？
29．计算：
（1）×（﹣9）﹣36×（）
（2）（）×（﹣6）+（﹣）2÷（﹣）3
30．若a、b互为相反数，c、d互为倒数，m的绝对值为2．
（1）直接写出a+b，cd，m的值；
（2）求m+cd+的值．
31．阅读下面的文字，完成后面的问题，我们知道：=1﹣，=﹣，=﹣，=﹣，……
那么：
（1）=　 　；
（2）用含有n（n为正整数）的式子表示你发现的规律　 　；
（3）求式子+++……．
32．计算：
（1）（1﹣1﹣+）÷（﹣）
（2）﹣25÷（﹣4）×（）2﹣12×（﹣15+24）3
33．阅读材料．
2017年10月18日，第十九次全国代表大会在人民大会堂隆重开幕．十九大提出，既要创造更多物质财富和精神财富以满足人民日益增长的美好生活需要，也要提供更多优质生态产品以满足人民日益增长的优美生态环境需要．必须坚持节约优先、保护优先、自然恢复为主的方针，形成节约资源和保护环境的空间格局、产业结构、生产方式、生活方式，还自然以宁静、和谐、美丽．
为了保护环境节约水资源，我市按照居民家庭年用水量实行阶梯水价，水价分档递增．居民用户按照以下的标准执行：第一阶梯上限180立方米，水费价格为5元/每立方米；第二阶梯为181﹣260立方米之间，水费价格7元/每立方米；第三阶梯为260立方米以上用水量，水价为9元/每立方米．如表所示：
供水类型
阶梯
户年用水量
（立方米）
水价
其中
水费
水资源费
污水处理费
自来水
第一阶梯
0﹣180（含）
5
2.07
1.57
1.36
第二阶梯
181﹣260（含）
7
4.07
第三阶梯
260以上
9
6.07
根据以上材料解决问题：
若小明家在2017年共用水200立方米，准备1000元的水费够用吗？说明理由．
34．先阅读下列材料，然后解答问题．
探究：用的幂的形式表示am?an的结果（m、为正整数）．
分析：根据乘方的意义，am?an=?==am+n．
（1）请根据以上结论填空：36×38=　 　，52×53×57=　 　，（a+b）3?（a+b）5=　 　；
（2）仿照以上的分析过程，用的幂的形式表示（am）n的结果（提示：将am看成一个整体）．
35．王红有5张写着以下数字的卡片，请按要求抽出卡片，完成下列各题：
（1）从中取出2张卡片，使这2张卡片上数字乘积最小，最小值是　 　．
（2）从中取出2张卡片，使这2张卡片数字相除商最大，最大值是　 　．
（3）从中取出除0以外的4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，（注：每个数字只能用一次，如：23×[1﹣（﹣2）]），请另写出一种符合要求的运算式子　 　．
36．我们常用的数是十进制数，如4657=4×103+6×102+5×101+7×100，数要用10个数码（又叫数字）：0、1、2、3、4、5、6、7、8、9，在电子计算机中用的二进制，只要两个数码：0和1，如二进制中110=1×22+1×21+0×20等于十进制的数6，110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53．那么二进制中的数101011等于十进制中的哪个数？
37．小明爸爸给小明出了一道题，说明他本月炒股的盈亏情况（单位：元）
股票
每股净赚（元）
股票
招商银行
+23
500
浙江医药
﹣（﹣2.8）
1000
晨光文具
﹣1.5
1500
金龙汽车
﹣1
2000
请你也来计算一下，小明爸爸本月投资炒股到底是赔了还是赚了？赔了或赚了多少元？
38．我们已经学习过“乘方”和“开方”运算，下面给同学们介绍一种新的运算，即对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作logaN=b．
例如：因为53=125，所以log5125=3；因为112=121，所以log11121=2．
（1）填空：log66=　 　，log381=　 　．
（2）如果log2（m﹣2）=3，求m的值．
（3）对于“对数”运算，小明同学认为有“logaMN=logaM?logaN（a＞0，a≠1，M＞0，N＞0）”，他的说法正确吗？如果正确，请给出证明过程；如果不正确，请说明理由，并加以改正．
39．观察下面的变形规律：
；；；…．
解答下面的问题：
（1）仿照上面的格式请写出=　 　；
（2）若n为正整数，请你猜想=　 　；
（3）基础应用：计算：．
（4）拓展应用1：解方程：=2016
（5）拓展应用2：计算：．
40．一个能被13整除的自然数我们称为“十三数”，“十三数”的特征是：若把这个自然数的末三位与末三位以前
的数字组成的数之差，如果能被13整除，那么这个自然数就一定能被13整除．例如：判断383357能不能被13整除，这个数的末三位数字是357，末三位以前的数字组成的数是383，这两个数的差是383﹣357=26，26能被13整除，因此383357是“十三数”．
（1）判断3253和254514是否为“十三数”，请说明理由．
（2）若一个四位自然数，千位数字和十位数字相同，百位数字与个位数字相同，则称这个四位数为“间同数”．
①求证：任意一个四位“间同数”能被101整除．
②若一个四位自然数既是“十三数”，又是“间同数”，求满足条件的所有四位数的最大值与最小值之差．
　

参考答案与试题解析
　
一．选择题（共10小题）
1．在数学课上，老师让甲、乙、丙、丁，四位同学分别做了一道有理数运算题，你认为做对的同学是（　　）
甲：9﹣32÷8=0÷8=0
乙：24﹣（4×32）=24﹣4×6=0
丙：（36﹣12）÷=36×﹣12×=16
丁：（﹣3）2÷×3=9÷1=9
A．甲 B．乙 C．丙 D．丁
【分析】先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
【解答】解：甲：9﹣32÷8=9﹣9÷8=7，原来没有做对；
乙：24﹣（4×32）=24﹣4×9=﹣12，原来没有做对；
丙：（36﹣12）÷=36×﹣12×=16，做对了；
丁：（﹣3）2÷×3=9÷×3=81，原来没有做对．
故选：C．
【点评】考查了有理数的混合运算，有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化．
　
2．十进制数278，记作278（10），其实278（10）=2×102+7×101+8×100，二进制数101（2）=1×22+0×21+1×20．有一个k（0＜k≤10为整数）进制数165（k），把它的三个数字顺序颠倒得到的k进制数561（k）是原数的3倍，则k=（　　）
A．10 B．9 C．8 D．7
【分析】依据定义列出关于k的方程求解即可．
【解答】解：由题意得：3（k2+6k+5）=5k2+6k+1，
解得：k=7或k=﹣1（舍去）．
故选：D．
【点评】本题主要考查的是科学记数法，依据定义列出关于k的方程是解题的关键．
　
3．规定★为：x★y=+．已知2★1=．则15★16的值为（　　）
A． B．﹣ C． D．或﹣
【分析】根据题意可列出方程求出A的值，最后代入求值即可．
【解答】解：由题意可知：2★1=，
∴+=，
解得：A=1，
∴15★16=+=．
故选：C．
【点评】此题考查了有理数的混合运算、分式的方程的解法，涉及新定义型运算，代入求值等问题，解题的关键是列出方程求出A的值．
　
4．已知|a+2|+（b+3）2=0，则下列式子的值最小是（　　）
A．a+b B．ab C．ba D．a﹣b
【分析】首先根据非负数的性质求出a、b的值，然后再代值求解．
【解答】解：由题意，得：a+2=0，b+3=0，
即a=﹣2，b=﹣3；
所以a+b=﹣5，ab=6，ba=，a﹣b=1，
故选：A．
【点评】本题考查了非负数的性质，初中阶段有三种类型的非负数：（1）绝对值；（2）偶次方；（3）二次根式（算术平方根）．当它们相加和为0时，必须满足其中的每一项都等于0．根据这个结论可以求解这类题目．
　
5．如图，现有3×3的方格，每个小方格内均有不同的数字，要求方格内每一行．每一列以及每一条对角线上的三个数字之和均相等，图中给出了部分数字，则P处对应的数字是（　　）
A．7 B．5 C．4 D．1
【分析】设下面中间的数为x，分别表示出相应的数，再根据每一列以及每一条对角线上的三个数字之和均相等，列出方程求解即可．
【解答】解：设下面中间的数为x，则三个数字之和为8+x，
8﹣3=5，
8+x﹣3﹣6=x﹣1，
8+x﹣2﹣（x﹣1）=7，
5+6+7﹣7﹣3=8，
如图所示：
P+6+8=7+6+5，
解得P=4．
故选：C．
【点评】此题主要考查有理数的加法，图形的变化规律，学习过程中注意培养自己的观察、分析能力．
　
6．规定：求若干个相同的有理数（均不等）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”一般地，把（a≠0）记作a，读作“a的圈n次方”．关于除方，下列说法错误的是（　　）
A．任何非零数的圈2次方都等于1
B．对于任何正整数n，1=1
C．3④=4③
D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数
【分析】根据定义依次判定即可．
【解答】解：A、任何非零数的圈2次方就是两个相同数相除，所以都等于1； 所以选项A正确；
B、因为多少个1相除都是1，所以对于任何正整数n，1都等于1； 所以选项B正确；
C、3④=3÷3÷3÷3=，4③=4÷4÷4=，则 3④≠4③； 所以选项C错误；
D、负数的圈奇数次方，相当于奇数个负数相除，则结果是负数，负数的圈偶数次方，相当于偶数个负数相除，则结果是正数．所以选项D正确；
本题选择说法错误的，
故选：C．
【点评】本题是有理数的混合运算，也是一个新定义的理解与运用；一方面考查了有理数的乘除法及乘方运算，另一方面也考查了学生的阅读理解能力；注意：负数的奇数次方为负数，负数的偶数次方为正数，同时对新定义，其实就是多个数的除法运算，要注意运算顺序．
　
7．取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．经过下面5步运算可得1，即：如图所示．如果自然数m恰好经过7步运算可得到1，则所有符合条件的m的值有（　　）
A．3个 B．4个 C．5个 D．6个
【分析】首先根据题意，应用逆推法，用1乘以2，得到2；用2乘以2，得到4；用4乘以2，得到8；用8乘以2，得到16；然后分类讨论，判断出所有符合条件的m的值为多少即可．
【解答】解：根据分析，可得
则所有符合条件的m的值为：128、21、20、3．
故选：B．
【点评】此题主要考查了探寻数列规律问题，考查了逆推法的应用，注意观察总结出规律，并能正确的应用规律．
　
8．定义一种关于整数n的“F”运算：
（1）当n是奇数时，结果为3n+5；
（2）当n是偶数时，结果是（其中k是使是奇数的正整数），并且运算重复进行．
例如：取n=58，第一次经F运算是29，第二次经F运算是92，第三次经F运算是23，第四次经F运算是74…；若n=9，则第2017次运算结果是（　　）
A．1 B．2 C．7 D．8
【分析】根据关于整数n的“F”运算：探究规律后即可解决问题；
【解答】解：由题意n=9时，第一次经F运算是32，第二次经F运算是1，第三次经F运算是8，第四次经F运算是1…
以后出现1、8循环，奇数次是8，偶数次是1，
∴第2017次运算结果8，
故选：D．
【点评】本题考查有理数的混合运算，关于整数n的“F”运算，解题的关键是理解题意，循环从特殊到一般的探究规律的方法，属于中考选择题中的压轴题．
　
9．如图，在一个由6个圆圈组成的三角形里，把1到6这6个数分别填入图的圆圈中，要求三角形的每条边上的三个数的和S都相等，那么S的最大值是（　　）
?
A．9 B．10 C．12 D．13
【分析】三个顶角分别是4，5，6，4与5之间是3，6和5之间是1，4和6之间是2，这样每边的和才能相等．
【解答】解：由图可知S=3+4+5=12．
故选：C．
【点评】考查了有理数的加法，解题关键是三角形的三个顶点的数字是1～6这6个数最大的三个数字．
　
10．计算机中常用的16进制是逢16进1的计算制，采用数字0﹣9和字母A﹣F共16个计数符号，这些符号与十进制的数对应关系如下表．
16进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如，用十六进制表示：E+D=1B，则A×B=（　　）
A．6E B．72 C．5F D．B0
【分析】首先计算出A×B的值，再根据十六进制的含义表示出结果．
【解答】解：∵A×B=10×11=110，
110÷16=6余14，
∴用十六进制表示110为6E．
故选：A．
【点评】此题考查有理数的混合运算，培养学生的阅读理解能力和知识迁移能力，解决问题的关键是理解十六进制的含义．
　
二．填空题（共15小题）
11．设x为非负实数，将x“四舍五入”到整数的值记为＜x＞（可读作尖括号x），即当非负实数x满足n﹣≤x＜n+时，其中n为整数，则＜x＞=n．如＜0.48＞=0，＜5.5＞=6，＜3.49＞=3．如果＜x﹣2.2＞=5，那么x的取值范围是　6.7≤x＜7.7　
【分析】利用对非负实数x“四舍五入”到整数的值记为＜x＞，进而得出x的取值范围..
【解答】解：∵＜x﹣2.2＞=5，
∴4.5≤x﹣2.2＜5.5
∴6.7≤x＜7.7．
故答案为：6.7≤x＜7.7．
【点评】此题主要考查了新定义以及一元一次不等式的应用，根据题意正确理解＜x＞的意义是解题关键．
　
12．一般的，如果ax=N（a＞0，且a≠1），那么x叫做以a为底N的对数，记作x=logaN．例如：由于23=8，所以3是以2为底8的对数，记作log28=3；由于a1=a，所以1是以a为底a的对数，记作logaa=1．
对数作为一种运算，有如下的运算性质：如果a＞0，且a≠1，M＞0，N＞0，那么：
（1）loga（M?N）=logaM+logaN；
（2）loga=logaM﹣logaN；
（3）logaMn=nlogaM．
根据上面的运算性质，计算log2（47×25）+log26﹣log23的结果是　20　．
【分析】直接利用已知公式进而将原式变形求出答案即可．
【解答】解：log2（47×25）+log26﹣log23
=log2（214×25）+（log22+log263）﹣log23
=log2219+log22+log263﹣log23
=19+1
=20．
故答案为：20．
【点评】此题主要考查了有理数的乘方，正确将原式变形是解题关键．
　
13．定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为（其中k是使为奇数的正整数），并且重复运算，如取n=26，则
则当n=898时，第2018次“F”运算的结果是　8　．
【分析】由n=898是偶数，所以第一次利用②进行计算，得到结果449成为奇数，然后再利用①计算得到结果是1352，接着利用②除以8才能成为奇数，结果为169，再利用①结果为512，利用②进行计算除以512，得出结果1就出现循环，利用这个规律即可求出结果．
【解答】解：第1次：=449，
第2次：3×449+5=1352，
第3次：=169，
第4次：3×169+5=512，
第5次：=1，
第6次：3×1+5=8，
第7次：=1，
…
∵（2018﹣5）÷2=1006…1，
∴第2018次“F”运算的结果是8．
故答案为：8．
【点评】本题考查有理数的混合运算，数字的变化规律，找出数字之间的运算规律，利用规律即可求出结果．
　
14．已知a是不等于﹣1的数，我们把称为a的和倒数．如：2的和倒数为=，已知a1=1，a2是a1的和倒数，a3是a2的和倒数．a4是a3的和倒数，…，依此类推，则a1?a2?a3…a10=　　．
【分析】首先根据新定义规则求出a1，a2，a3，a4，a5…a10，求解即可．
【解答】解：a1=1，a2=，a3==，，，，，，，，
则a1?a2?a3…a10=1×=．
故答案为：．
【点评】本题考查了倒数，解决本题的关键是明确新定义．
　
15．如图，程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行程序框图，如果输入a，b的值分别为3，9，那么输出a的值为　3　．
【分析】根据程序框图先判断，再执行，分别计算出当前的a、b的值，从而得到结论．
【解答】解：当a=3、b=9时，b=9﹣3=6；
此时a=3、b=6，b=6﹣3=3，
则a=b=3，
所以输出a的值为3，
故答案为：3．
【点评】本题主要考查程序框图和算法，解题的关键是掌握循环结构的理解和应用及赋值语句的运用．
　
16．【阅读材料】“九宫图”源于我国古代夏禹时期的“洛书”（图1所示），是世界上最早的矩阵，又称“幻方”，用今天的数学符号翻译出来，“洛书”就是一个三阶“幻方”（图2所示）．
【规律总结】观察图1、图2，根据“九宫图”中各数字之间的关系，我们可以总结出“幻方”需要满足的条件是　每一行、每一列和每条对角线上各个数之和都相等　；若图3，是一个“幻方”，则a=　﹣3　．
【分析】根据题意确定出“幻方”需要的条件，确定出a的值即可．
【解答】解：【阅读材料】“九宫图”源于我国古代夏禹时期的“洛书”（图1所示），是世界上最早的矩阵，又称“幻方”，用今天的数学符号翻译出来，“洛书”就是一个三阶“幻方”（图2所示）．
【规律总结】观察图1、图2，根据“九宫图”中各数字之间的关系，我们可以总结出“幻方”需要满足的条件是每一行、每一列和每条对角线上各个数之和都相等；若图3，是一个“幻方”，则4+1+（﹣2）=4+2+a，即a=﹣3，
故答案为：每一行、每一列和每条对角线上各个数之和都相等；﹣3
【点评】此题考查了有理数的加法，弄清题意是解本题的关键．
　
17．某公园划船项目收费标准如下：
船型
两人船（限乘两人）
四人船（限乘四人）
六人船（限乘六人）
八人船（限乘八人）
每船租金（元/小时）
90
100
130
150
某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为　380　元．
【分析】分四类情况，分别计算即可得出结论．
【解答】解：∵共有18人，
当租两人船时，∴18÷2=9（艘），∵每小时90元，∴租船费用为90×9=810元，
当租四人船时，∵18÷4=4余2人，∴要租4艘四人船和1艘两人船，∵四人船每小时100元，
∴租船费用为100×4+90=490元，
当租六人船时，∵18÷6=3（艘），∵每小时130元，∴租船费用为130×3=390元，
当租八人船时，∵18÷8=2余2人，∴要租2艘八人船和1艘两人船，∵8人船每小时150元，
当租1艘四人船，1艘6人船，1艘8人船，100+130+150=380元
∴租船费用为150×2+90=390元，而810＞490＞390＞380，
∴当租1艘四人船，1艘6人船，1艘8人船费用最低是380元，
故答案为：380．
【点评】此题主要考查了有理数的运算，用分类讨论的思想解决问题是解本题的关键．
　
18．下面是一种算法：输入任意一个数x，都是“先乘以2，再减去3”，进行第1次这样的运算，结果为y1，再对y1实施同样的运算，称为第2次运算，结果为y2，这样持续进行，要使第n次运算结果为0，即yn=0，则最初输入的数应该是　3﹣　．（用含有n的代数式表示）．
【分析】根据题意列出式子即可．
【解答】解：根据题意得：最初输入的数应该是3﹣，
故答案为：3﹣
【点评】此题考查了有理数的乘法，减法，熟练掌握运算法则是解本题的关键．
　
19．现定义两种运算“⊕”和“※”．对于任意两个整数，a⊕b=a+b﹣1，a※b=a×b﹣1，则8※（3⊕5）=　55　．
【分析】原式利用题中的新定义计算即可求出值．
【解答】解：根据题中的新定义得：原式=8※7=56﹣1=55，
故答案为：55
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
　
20．已知：C==3，C==10，C==15，…，观察上面的计算过程，寻找规律并计算：C=　4　．
【分析】根据=计算可得．
【解答】解：C==4，
故答案为：4．
【点评】本题主要考查有理数的乘法，解题的关键是根据已知等式得出计算公式．
　
21．在图（1）中，对任意相邻的上下或左右两格中的数字同时加1或减2，这算作一次操作，经过若干次操作后，图（1）能变为图（2），则图（2）中A格内的数是　4　
【分析】每次变换都是在相邻的两格，则将相邻的两格区分出来，如解答中图的有阴影和无阴影．由题可知，每次变换都是阴影格中的一个数据和无阴影格中的一个数据同时加1或减2，所以无论变换多少次，所有阴影格中的数字之和与所有无阴影格中的数字之和的差不变．
【解答】解：如图，将相邻两格用阴影区分出来．
由于每次变换都是一个阴影格和相邻的无阴影格中的数据同时加1或减2，所以变换过程中，所有阴影格中的数字之和与所有无阴影格中的数字之和的差不变．
图（1）中对应的阴影格的数字之和为：0+5+2+7+8+5+0+6=33，
图（1）中对应的无阴影格的数字之和为：1+4+3+6+4+5+2+4=29，
图（2）中对应的阴影格的数字之和为：1+A+1=2+A，
图（2）中对应的无阴影格的数字之和为：1+1=2，
由上述分析可知：33﹣29=2+A﹣2，
则可得A=4．
故答案为：4．
【点评】解答此题的关键是将相邻两格区分出来，然后根据两部分之和的差求解．
　
22．将一张长方形的纸按如图对折，对折时每次折痕与上次的折痕保持平行，第一次对折后可得到1条折痕（图中虚线），第二次对折后可得到3条折痕，第三次对折后得到7条折痕，那么第10次对折后得到的折痕比第9次对折后得到的折痕多　29　条．
【分析】由题意得出对折n+1次比对折n次折痕多2n条，据此可得．
【解答】解：∵对折2次比对折1次折痕多3﹣1=2条，
对折3次比对折2次折痕多7﹣3=4=22条，
对折4次比对折3次折痕多15﹣7=8=23条，
……
∴对折10次比对折9次折痕多29条，
故答案为：29．
【点评】本题主要考查有理数的乘方，解题的关键是根据题意得出对折n+1次比对折n次折痕多2n条．
　
23．将一张厚度均匀的纸反复对折，对折3次后，折成的纸的厚度为10mm，如果要使折成的厚度为40mm，那么对折的次数为　5　次．
【分析】根据对折规律，对折后的厚度成2的指数次幂变化，写出即可．
【解答】解：由题意可知：设一张纸的厚度为xmm，
对折1次后，纸的厚度为2×x；
对折2次后，纸的厚度为2×2x=22×x；
对折3次后，纸的厚度为2×2×2x=23×x=10；
解得：x=1.25，
对折n次后，纸的厚度为2×2×2×2×…×2×1.25=2n×1.25=40，
解得：n=5．
故答案为：5．
【点评】本题考查了有理数的乘方的理解，理解对折后厚度变为原来的2倍，有关数据成2的指数幂变化或接近2的指数幂变化是解题的关键．
　
24．观察下列等式：=×（1﹣），=×（﹣），=×（﹣），=×（﹣），…
根据你得出的规律写出第n个等式为　=×（﹣）　，并根据该规律计算：+++…+=　　．
【分析】根据等式的左边分母是n2+2n，右边是乘以﹣的差，再把式子展开，进行合并即可．
【解答】解：第n个等式为=×（﹣），
+++…+=×（1﹣）+×（﹣）+×（﹣）+…+×（﹣）
=×（1﹣+﹣+﹣+…+﹣）
=×（1+﹣﹣）
=×
=．
故答案为=×（﹣），．
【点评】本题考查了有理数的混合运算，本题是一个找规律的题目，找到第n个式子是解题的关键．
　
25．某种细胞开始有两个，1小时后分裂成4个并死去一个，2个小时后分裂成6个并死去一个，3小时后分裂成10个并死去1个，按此规律，请你计算经过n个小时后，细胞存活的个数为　（2n+1）　个（结果用含n的代数式表示）
【分析】根据细胞分裂过程，归纳总结得到一般性规律，即可得到结果．
【解答】解：根据题意得：按此规律，6小时后存活的个数是26+1=65个，经过n个小时后，细胞存活的个数为2n+1（个）．
故答案为：（2n+1）．
【点评】此题考查了有理数的乘方，弄清题意是解本题的关键．
　
三．解答题（共15小题）
26．计算：
（1）（+25）﹣（﹣10）
（2）（﹣）+（+）
（3）12﹣（﹣18）+（﹣7）﹣15+（﹣18）
（4）﹣42×（﹣）3+（﹣3）2÷（﹣）2
【分析】（1）根据有理数的加减法可以解答本题；
（2）根据有理数的加法可以解答本题；
（3）根据有理数的加减法可以解答本题；
（4）根据有理数的加减法和乘除法可以解答本题；．
【解答】解：（1）（+25）﹣（﹣10）
=25+10
=35；
（2）（﹣）+（+）
=（﹣）+
=；
（3）12﹣（﹣18）+（﹣7）﹣15+（﹣18）
=12+18+（﹣7）+（﹣15）+（﹣18）
=﹣10；
（4）﹣42×（﹣）3+（﹣3）2÷（﹣）2
=﹣16×（﹣）+9÷
=2+9×
=2+4
=6．
【点评】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．
　
27．已知x，y为有理数，现规定一种新运算*，满足x*y=xy﹣2x+1
（1）求3*2的值；
（2）对于任意两个有理数x，y，是否都有x*y=y*x成立？如果成立，请证明，如果不成立，请举反例说明；
（3）如图，数轴上线段AB=2（单位长度），CD=4（单位长度），点A在数轴上表示的数是1*（﹣9），点C在数轴上表示的数是（﹣8）*．若线段AB以6个单位长度每秒的速度向右匀速运动，同时线段CD以2个单位长度每秒的速度向左匀速运动．问运动多少秒时，BC=8（单位长度）？此时点B在数轴上表示的数是多少．
【分析】（1）根据新定义代入求值即可；
（2）举反例说明不成立：当x=3，y=2时，代入计算；
（3）先根据新定义计算点A、B、C在数轴上表示的数，设运动t秒时，BC=8（单位长度），分两种情况：根据BC=8列方程可得结论．
【解答】解：（1）3*2=3×2﹣2×3+1=1
（2）不成立，
当x=3，y=2时，x*y=3*2=3×2﹣2×3+1=1，
y*x=2*3=2×3﹣2×2+1=6﹣4+1=3，
∴对于任意两个有理数x，y，x*y=y*x不一定成立；
（3）∵点A在数轴上表示的数是1*（﹣9）=1×（﹣9）﹣2×1+1=﹣10，
∵AB=2，
∴点B在数轴上表示的数是：﹣8，
∵点C在数轴上表示的数是（﹣8）*=﹣8×﹣2×（﹣8）+1=16，
设运动t秒时，BC=8（单位长度），
分两种情况：
①当点B在点C的左侧时，
由题意得：（16﹣2t）﹣（﹣8+6t）=8，
t=2，
此时点B在数轴上表示的数是：﹣8+6t=﹣8+12=4，
②当点B在点C的右侧时，
由题意得：（﹣8+6t）﹣（16﹣2t）=8，
t=4，
此时点B在数轴上表示的数是：﹣8+6t=﹣8+24=16．
【点评】本题主要考查有理数的混合运算和数轴的性质，熟练掌握新运算的公式、有理数的混合运算的顺序和法则是解题的关键．
　
28．有依次排列的3个数：3，9，8，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，﹣1，8，这称为第一次操作；第二次同样的操作后也可产生一个新数串：3，3，6，3，9，﹣10，﹣1，9，8；继续依次操作下去．问
（1）第一次操作后，增加的所有新数之和是多少？
（2）第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和是多少？
（3）猜想：第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和是多少？
【分析】（1）先求得增加的新数，然后再依据加法法则进行计算即可；
（2）先依据题目求得第二次操作后所得增加的新数字，然后再进行计算即可；
（3）先找出其中的规律，然后，依据规律进行计算即可．
【解答】解：（1）第一次操作后增加的新数是6，﹣1，则6+（﹣1）=5．
（2）第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和为3+3+（﹣10）+9=5．
（3）猜想：第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和为5．
【点评】本题主要考查的是有理数的减法，熟练掌握有理数的减法法则是解题的关键．
　
29．计算：
（1）×（﹣9）﹣36×（）
（2）（）×（﹣6）+（﹣）2÷（﹣）3
【分析】（1）先算乘除，后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．注意乘法分配律的灵活运用；
（2）先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
【解答】解：（1）×（﹣9）﹣36×（）
=﹣6﹣36×+36×﹣36×
=﹣6﹣20+27﹣3
=﹣2；
（2）（）×（﹣6）+（﹣）2÷（﹣）3
=﹣×（﹣6）+÷（﹣）
=1﹣2
=﹣1．
【点评】考查了有理数的混合运算，有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化．
　
30．若a、b互为相反数，c、d互为倒数，m的绝对值为2．
（1）直接写出a+b，cd，m的值；
（2）求m+cd+的值．
【分析】（1）根据互为相反数的和为0，互为倒数的积为1，绝对值的意义，即可解答；
（2）分两种情况讨论，即可解答．
【解答】解：（1）∵a、b互为相反数，c、d互为倒数，m的绝对值为2，
∴a+b=0，cd=1，m=±2．
（2）当m=2时，m+cd+=2+1+0=3；
当m=﹣2时，m+cd+=﹣2+1+0=﹣1．
【点评】本题考查了倒数、相反数、绝对值，解决本题的关键是熟记倒数、相反数、绝对值的意义．
　
31．阅读下面的文字，完成后面的问题，我们知道：=1﹣，=﹣，=﹣，=﹣，……
那么：
（1）=　﹣　；
（2）用含有n（n为正整数）的式子表示你发现的规律　　；
（3）求式子+++……．
【分析】（1）根据阅读材料中的方法变形即可；
（2）归纳总结得到一般性规律，写出即可；
（3）原式利用得出的规律变形，计算即可求出值．
【解答】解：（1）=﹣；
（2）根据题意得：=﹣；
（3）原式=1﹣+﹣+…+﹣=1﹣=．
故答案为：（1）﹣；
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
　
32．计算：
（1）（1﹣1﹣+）÷（﹣）
（2）﹣25÷（﹣4）×（）2﹣12×（﹣15+24）3
【分析】（1）除法转化为乘法，再运用乘法分配律计算可得；
（2）根据有理数混合运算顺序和运算法则计算可得．
【解答】解：（1）原式=（1﹣1﹣+）×（﹣24）
=﹣24+36+9﹣14
=7；
（2）原式=﹣32×（﹣）×﹣12×（﹣15+16）3
=2﹣12×1
=2﹣12
=﹣10．
【点评】本题主要考查有理数的混合运算，解题的关键是熟练掌握有理数的混合运算顺序和运算法则．
　
33．阅读材料．
2017年10月18日，第十九次全国代表大会在人民大会堂隆重开幕．十九大提出，既要创造更多物质财富和精神财富以满足人民日益增长的美好生活需要，也要提供更多优质生态产品以满足人民日益增长的优美生态环境需要．必须坚持节约优先、保护优先、自然恢复为主的方针，形成节约资源和保护环境的空间格局、产业结构、生产方式、生活方式，还自然以宁静、和谐、美丽．
为了保护环境节约水资源，我市按照居民家庭年用水量实行阶梯水价，水价分档递增．居民用户按照以下的标准执行：第一阶梯上限180立方米，水费价格为5元/每立方米；第二阶梯为181﹣260立方米之间，水费价格7元/每立方米；第三阶梯为260立方米以上用水量，水价为9元/每立方米．如表所示：
供水类型
阶梯
户年用水量
（立方米）
水价
其中
水费
水资源费
污水处理费
自来水
第一阶梯
0﹣180（含）
5
2.07
1.57
1.36
第二阶梯
181﹣260（含）
7
4.07
第三阶梯
260以上
9
6.07
根据以上材料解决问题：
若小明家在2017年共用水200立方米，准备1000元的水费够用吗？说明理由．
【分析】根据收费标准求出年用水200立方米的应缴费用，将其与1000比较后即可得出结论．
【解答】解：180×5+（200﹣180）×7，
=900+140，
=1040（元）．
∵1040＞1000，
∴准备1000元的水费不够．
【点评】本题考查了有理数的混合运算，根据收费标准求出小明家2017年应缴水费是解题的关键．
　
34．先阅读下列材料，然后解答问题．
探究：用的幂的形式表示am?an的结果（m、为正整数）．
分析：根据乘方的意义，am?an=?==am+n．
（1）请根据以上结论填空：36×38=　314　，52×53×57=　512　，（a+b）3?（a+b）5=　（a+b）8　；
（2）仿照以上的分析过程，用的幂的形式表示（am）n的结果（提示：将am看成一个整体）．
【分析】（1）根据结论，同底数幂相乘，底数不变指数相加进行计算即可得解；
（2）将am看成一个整体，根据乘方的意义解答．
【解答】解：（1）36×38=36+8=314；
52×53×57=52+3+7=512；
（a+b）3?（a+b）5=（a+b）3+5=（a+b）8；
故答案为：314；512；（a+b）8；
（2）（am）n==amn．
【点评】本题考查了有理数的乘方，有理数的乘法，读懂题目信息，理解有理数的乘方的意义是解题的关键．
　
35．王红有5张写着以下数字的卡片，请按要求抽出卡片，完成下列各题：
（1）从中取出2张卡片，使这2张卡片上数字乘积最小，最小值是　﹣6　．
（2）从中取出2张卡片，使这2张卡片数字相除商最大，最大值是　3　．
（3）从中取出除0以外的4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，（注：每个数字只能用一次，如：23×[1﹣（﹣2）]），请另写出一种符合要求的运算式子　[3﹣（﹣2）]2﹣1=24　．
【分析】（1）根据题意列出算式，找出积最大值即可；
（2）根据题意列出算式，找出商最小值即可；
（3）利用“24点”游戏规则列出算式即可；
【解答】解：（1）取3，﹣2，乘积最小=﹣6，
故答案为﹣6．
（2）取3，1商的最大值为3，
故答案为3．
（3）[3﹣（﹣2）]2﹣1=24
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键，记住先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
　
36．我们常用的数是十进制数，如4657=4×103+6×102+5×101+7×100，数要用10个数码（又叫数字）：0、1、2、3、4、5、6、7、8、9，在电子计算机中用的二进制，只要两个数码：0和1，如二进制中110=1×22+1×21+0×20等于十进制的数6，110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53．那么二进制中的数101011等于十进制中的哪个数？
【分析】利用新定义得到101011=1×25+0×24+1×23+0×22+1×21+1×20，然后根据乘方的定义进行计算．
【解答】解：101011=1×25+0×24+1×23+0×22+1×21+1×20=43，
所以二进制中的数101011等于十进制中的43．
【点评】本题考查了有理数的乘方：有理数乘方的定义：求n个相同因数积的运算，叫做乘方．
　
37．小明爸爸给小明出了一道题，说明他本月炒股的盈亏情况（单位：元）
股票
每股净赚（元）
股票
招商银行
+23
500
浙江医药
﹣（﹣2.8）
1000
晨光文具
﹣1.5
1500
金龙汽车
﹣1
2000
请你也来计算一下，小明爸爸本月投资炒股到底是赔了还是赚了？赔了或赚了多少元？
【分析】首先分别求出招商银行、浙江医药、晨光文具、金龙汽车这4种股票分别赚了多少钱；然后把它们相加，判断出投资者到底是赔了还是赚了，赔了或赚了多少元即可．
【解答】解：天河：500×23 +2.8×1000﹣1.5×1500﹣1.8×2000
=4000+2800﹣2250﹣3600
=950（元）
答：赚了，赚了950元．
【点评】此题主要考查了有理数的乘方的含义和求法，以及有理数的加减法的运算方法，要熟练掌握．
　
38．我们已经学习过“乘方”和“开方”运算，下面给同学们介绍一种新的运算，即对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作logaN=b．
例如：因为53=125，所以log5125=3；因为112=121，所以log11121=2．
（1）填空：log66=　1　，log381=　4　．
（2）如果log2（m﹣2）=3，求m的值．
（3）对于“对数”运算，小明同学认为有“logaMN=logaM?logaN（a＞0，a≠1，M＞0，N＞0）”，他的说法正确吗？如果正确，请给出证明过程；如果不正确，请说明理由，并加以改正．
【分析】（1）根据新定义由61=6、34=81可得log66=1，log381=4；
（2）根据定义知m﹣2=23，解之可得；
（3）设ax=M，ay=N，则logaM=x、logaN=y，根据ax?ay=ax+y知ax+y=M?N，继而得logaMN=x+y，据此即可得证．
【解答】解：（1）∵61=6，34=81，
∴log66=1，log381=4，
故答案为：1、4；
（2）∵log2（m﹣2）=3，
∴m﹣2=23，解得：m=10；
（3）不正确，
设ax=M，ay=N，
则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
∵ax?ay=ax+y，
∴ax+y=M?N，
∴logaMN=x+y，
即logaMN=logaM+logaN．
【点评】本题考查有理数和整式的混合运算，解题的关键是明确题意，可以利用新定义进行解答问题．
　
39．观察下面的变形规律：
；；；…．
解答下面的问题：
（1）仿照上面的格式请写出=　﹣　；
（2）若n为正整数，请你猜想=　﹣　；
（3）基础应用：计算：．
（4）拓展应用1：解方程：=2016
（5）拓展应用2：计算：．
【分析】（1）根据上述等式得出拆项规律；
（2）归纳总结得到一般性规律，写出即可；
（3）利用得出的规律将原式变形，计算即可得到结果．
（4）根据得出的规律将方程变形为：=2016，系数化为1可得方程的解；
（5）根据==，将原式依次变形可得结果．
【解答】（满分12分）
解：（1）=﹣； …（2分）
（2）=﹣；…（2分）
（3）计算：．
=1﹣+﹣+﹣+…+﹣．
=1﹣．
=；…（2分）
（4）=2016，
x（1﹣+﹣+﹣+…+﹣）=2016，
=2016，
x=2017；…（3分）
（5）．
=（1﹣）+（）+（﹣）+…+（﹣）．
=（1﹣）．
=．…（3分）
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
　
40．一个能被13整除的自然数我们称为“十三数”，“十三数”的特征是：若把这个自然数的末三位与末三位以前
的数字组成的数之差，如果能被13整除，那么这个自然数就一定能被13整除．例如：判断383357能不能被13整除，这个数的末三位数字是357，末三位以前的数字组成的数是383，这两个数的差是383﹣357=26，26能被13整除，因此383357是“十三数”．
（1）判断3253和254514是否为“十三数”，请说明理由．
（2）若一个四位自然数，千位数字和十位数字相同，百位数字与个位数字相同，则称这个四位数为“间同数”．
①求证：任意一个四位“间同数”能被101整除．
②若一个四位自然数既是“十三数”，又是“间同数”，求满足条件的所有四位数的最大值与最小值之差．
【分析】（1）根据“十三数”的特征，列出算式求解即可；
（2）①设任意一个四位“间同数”为（1≤a≤9，0≤b≤9，a、b为整数），列式计算可得10a+b，从而求解；
②同理设出这个四位“间同数”为（1≤a≤9，0≤b≤9，a、b为整数），可知101b+9a是13的倍数，分别讨论可得结论．
【解答】（1）解：3253不是“十三数”，254514是“十三数”，理由如下：（1分）
∵3﹣253=﹣250，不能被13整除，
∴3253不是“十三数”，（2分）
∵254﹣514=﹣260，﹣260÷13=﹣20
∴254514是“十三数”；（3分）
（2）①证明：设任意一个四位“间同数”为（1≤a≤9，0≤b≤9，a、b为整数），
∵===10a+b，（5分）
∵a、b为整数，
∴10a+b是整数，
即任意一个四位“间同数”能被101整除；（6分）
②解：设任意一个四位“间同数”为（1≤a≤9，0≤b≤9，a、b为整数），
∵=，（7分）
∵这个四位自然数是“十三数”，
∴101b+9a是13的倍数，（8分）
当a=1，b=3时，101b+9a=303+9=312，312÷13=24，此时这个四位“间同数”为：1313；
当a=2，b=6时，101b+9a=606+18=624，624÷13=48，此时这个四位“间同数”为：2626；
当a=3，b=9时，101b+9a=909+27=736，936÷13=72，此时这个四位“间同数”为：3939；
当a=5，b=2时，101b+9a=202+45=247，247÷13=19，此时这个四位“间同数”为：5252；
当a=6，b=5时，101b+9a=505+54=559，559÷13=43，此时这个四位“间同数”为：6565；
当a=7，b=8时，101b+9a=808+63=871，871÷13=67，此时这个四位“间同数”为：7878；
当a=9，b=1时，101b+9a=101+81=182，182÷13=14，此时这个四位“间同数”为：9191；
综上可知：这个四位“间同数”最大为9191，最小为1313，
9191﹣1313=7878，
则满足条件的所有四位数的最大值与最小值之差为7878．（12分）
【点评】此题主要考查了新定义，数的整除，解本题的关键是理解新定义，掌握数的整除是解本题的难点．