5.5 一次函数的简单应用(2)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 5.5 一次函数的简单应用(2)(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 379.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 00:00:00 | ||
图片预览



文档简介
浙江版八年级数学上册第5章5.5一次函数的简单应用
第2课时 一次函数的简单应用(2)
【知识清单】
一、一次函数的表达式的应用:
从“数”的方面看当一次函数y=kx+b(k、b为常数,k≠0)的函数值为0(即y=0)时,则自变量x的值,即为方程kx+b=0的解;从“形”的方面看函数图象与x轴交点的横坐标x的值,即为方程kx+b=0的解.
二、由两条相交的函数图象可获取的信息:
1.交点坐标用(x0,y0)表示,当x= x0,两函数值相等;
2.对于同一自变量来说,函数图象在上方,说明函数值大;反之函数值小.
【经典例题】
例题1、小明家与爷爷家相距36km,小明7点从家出发,骑自行车回爷爷家,哥哥有事要处理从家出发比弟弟晚一个小时,乘车沿相同路线回爷爷家,小明和哥哥的行进路程S(km)与时间t(时)的函数图象如图所示,则下列说法中错误的有( )
①小明骑自行车的平均速度是12km/h;②9点之前哥哥的速度比弟弟的慢;③哥哥在距爷爷家12km处追上小明;④哥哥比弟弟提前30分钟到爷爷家.
A.1个 B.2个 C.3个 D.4个
【考点】一次函数图象的应用.
【分析】由图象可知,小明骑完全程用了3小时,而哥哥用了1.5小时,二人的行程都是36千米可根据公式S=tv进行计算平均速度;两个图象的交点表示二人在同一时刻到达相同的位置,由图象可知9:00二人相遇,由此可分析其行程.
【解答】①∵小明到爷爷家用时107=3(小时),行程36千米,
∴v=36÷3=12km/h.
??? 故:①正确.
②∵哥哥到爷爷家用时9.58=1.5(小时),行程36千米,
∴v=36÷1.5=24km/h,24>12 .
????????? ? 故:②错误.
③∵二人在9:00相遇,此时小明已骑车2小时,哥哥出发1小时,
∴哥哥的行程=24×1=24(千米),小明的行程=12×2=24(千米),
∴3624=12,
哥哥在距爷爷家12km处追上小明.
? ? 故:③正确.
?? ④∵哥哥到爷爷家的时间为9.5小时,弟弟到爷爷家的时间为10小时,
? 109.5=0.5(小时),0.5时=30分钟.
即:④正确.
故:选A .
【点评】本题考查了函数图象的意义、性质;认真读图、分析变量t、S的意义及取值是解题的关键,本题考查了一次函数的应用,解决本题的关键是读懂函数图象,获取有效信息.
例题2、一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶60千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图像
【考点】一次函数图象的应用.
【分析】(1)设线段AB的解析式为y=kx+b,将(2,140),(3,0)代入,可求线段AB的解析式,根据线段AB的解析式求A点坐标,得出甲乙两地之间的距离;(2)根据相遇时:快车路程+慢车路程=甲乙两地距离,利用t=甲乙两地距离÷快车速度,求t.
【解答】如图①(1)线段AB所在直线的函数解析式为:y=kx+b,
将(2,140)、(3,0)代入得:
,解得,
所以线段AB所在直线的函数解析式为:y=140x+420,
当x=0时, y=420,
所以甲乙两地之间的距离420千米.
(2)设快车的速度为m千米/时,慢车的速度为n千米/时,
由题意得:
,解得,
所以快车的速度为80千米/时,所以
(3)如图②所示.?
【点评】本题考查了一次函数的运用.关键是通过图象,求出直线解析式,利用直线解析式求A点坐标,得出甲乙两地距离,再根据路程、速度、时间的关系解题.
【夯实基础】
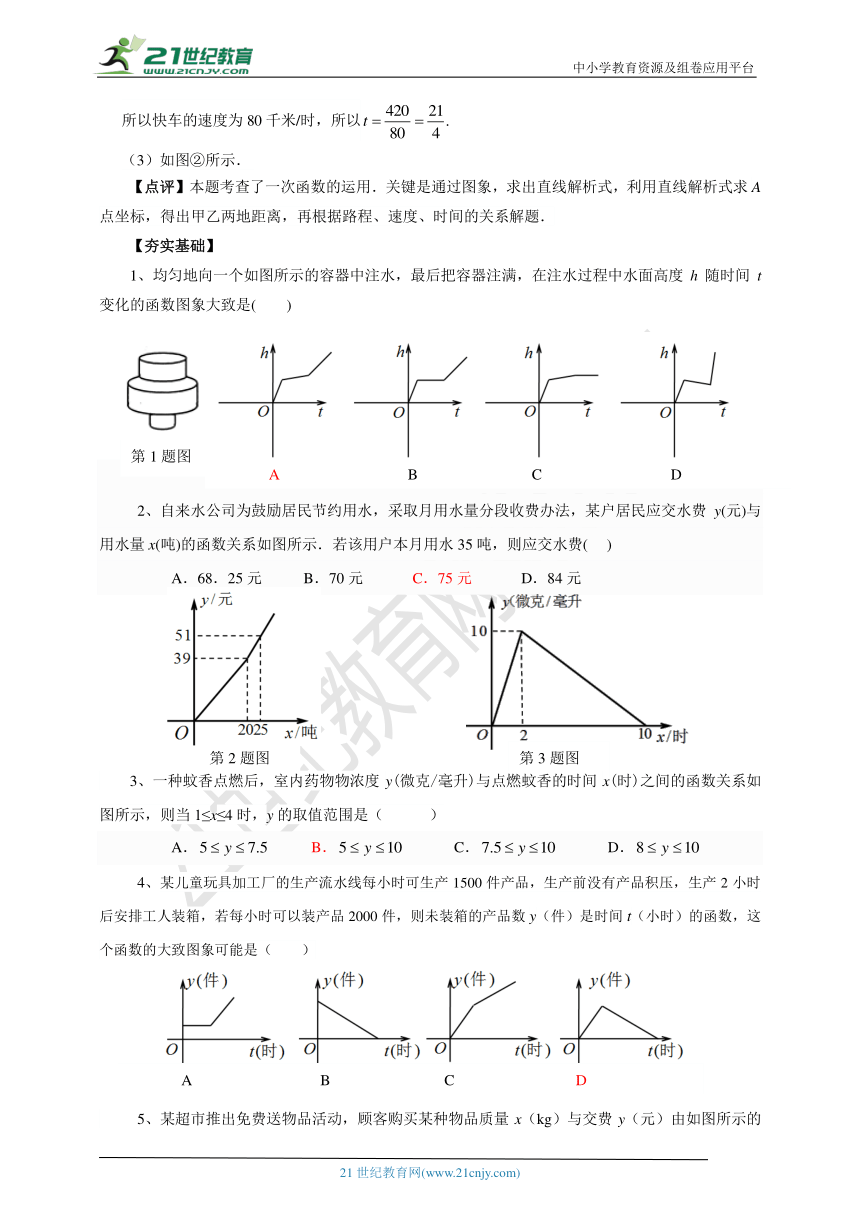
1、均匀地向一个如图所示的容器中注水,最后把容器注满,在注水过程中水面高度h随时间t变化的函数图象大致是( )
2、自来水公司为鼓励居民节约用水,采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水35吨,则应交水费(??? )
?A.68.25元? B.70元??? C.75元?? ?D.84元
3、一种蚊香点燃后,室内药物物浓度y(微克/毫升)与点燃蚊香的时间x(时)之间的函数关系如图所示,则当1≤x≤4时,y的取值范围是( )
?A.? B.??? C.?? ?D.
4、某儿童玩具加工厂的生产流水线每小时可生产1500件产品,生产前没有产品积压,生产2小时后安排工人装箱,若每小时可以装产品2000件,则未装箱的产品数y(件)是时间t(小时)的函数,这个函数的大致图象可能是( )
5、某超市推出免费送物品活动,顾客购买某种物品质量x(kg)与交费y(元)由如图所示的一次函数图象确定,则顾客可以免费领取物品的最最小质量为__20____kg.
6、如图,小明购买一种羽毛球所付款金额y(元)与购买量x(个)之间的函数图象由线段OA和射线AB组成,则一次购买10个羽毛球比分10次购买每次购买1个可节省 .
7、栽种了一颗20cm高的玉米苗,它的生长高度y(厘米)与时间x(天)的关系,并画出如图所示的图象(AB是线段,直线BC平行x轴).
(1)这颗玉米,多少天以后停止长高?
(2)求直线AC的解析式,并求这颗玉米最高长多少厘米?
8、某产品生产车间有工人20名.已知每名工人每天可生产甲种产品24个或乙种产品20个,且每生产一个甲种产品可获得利润120元,每生产一个乙种产品可获得利润200元.在这20名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)请写出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为64320元,要派多少名工人去生产甲种产品?
(3)若生产甲种产品的人数大于生产乙种产品人数的,而小于生产乙种产品人数的,要使获取利润最大,你认为安排多少名工人去生产乙种产品才合适?
【提优特训】
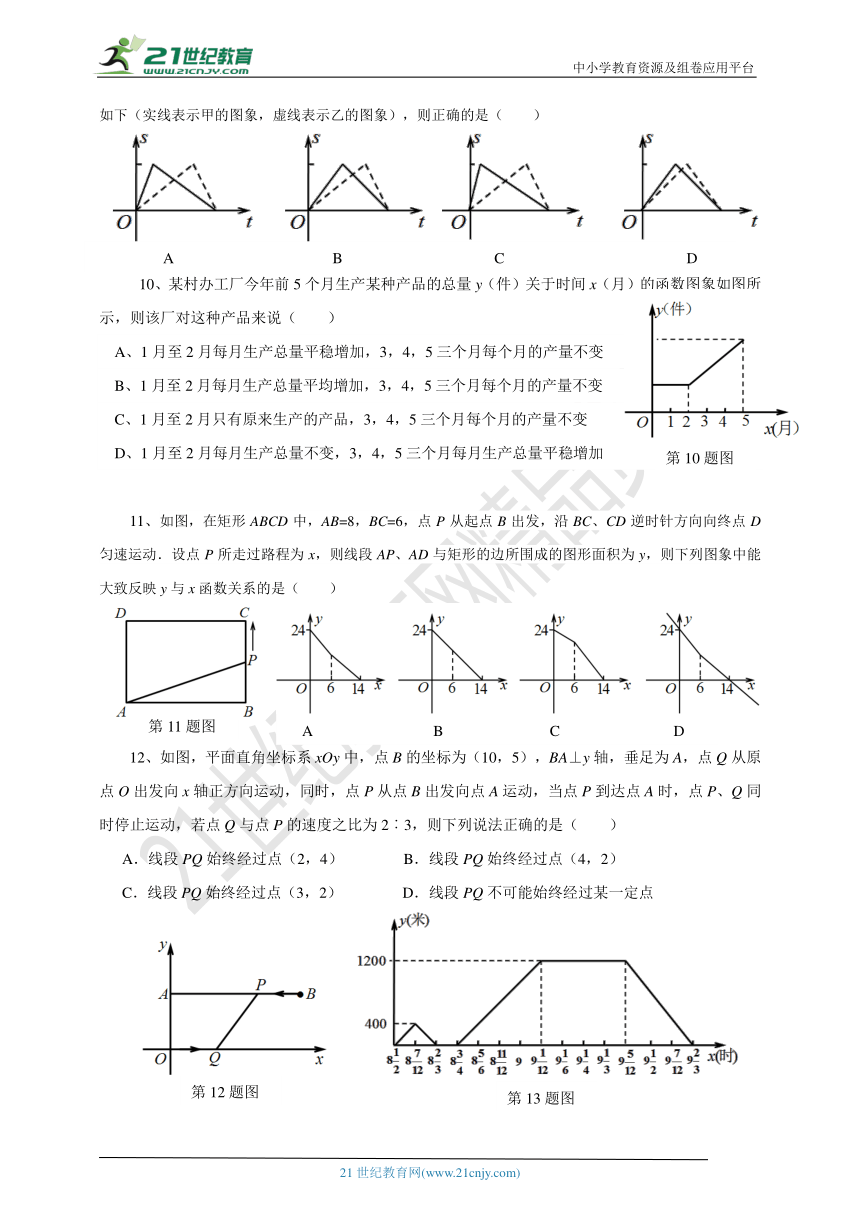
9、某校举行趣味运动会,甲、乙两名学生同时从A地到B地,甲先骑自行车到B地后跑步回A地,乙则是先跑步到B地后骑自行车回A地(骑自行车的速度快于跑步的速度),最后两人恰好同时回到A地.已知甲骑自行车比乙骑自行车的速度快.若学生离A地的距离s与所用时间t的函数关系用图象表示如下(实线表示甲的图象,虚线表示乙的图象),则正确的是( )
10、某村办工厂今年前5个月生产某种产品的总量y(件)关于时间x(月)的函数图象如图所示,则该厂对这种产品来说( )
A、1月至2月每月生产总量平稳增加,3,4,5三个月每个月的产量不变
B、1月至2月每月生产总量平均增加,3,4,5三个月每个月的产量不变
C、1月至2月只有原来生产的产品,3,4,5三个月每个月的产量不变
D、1月至2月每月生产总量不变,3,4,5三个月每月生产总量平稳增加
11、如图,在矩形ABCD中,AB=8,BC=6,点P从起点B出发,沿BC、CD逆时针方向向终点D匀速运动.设点P所走过路程为x,则线段AP、AD与矩形的边所围成的图形面积为y,则下列图象中能大致反映y与x函数关系的是( )
12、如图,平面直角坐标系xOy中,点B的坐标为(10,5),BA⊥y轴,垂足为A,点Q从原点O出发向x轴正方向运动,同时,点P从点B出发向点A运动,当点P到达点A时,点P、Q同时停止运动,若点Q与点P的速度之比为2︰3,则下列说法正确的是( )
A.线段PQ始终经过点(2,4) B.线段PQ始终经过点(4,2)
C.线段PQ始终经过点(3,2) D.线段PQ不可能始终经过某一定点
13、星期日上午8点30分李峰从家中出发骑自行车到距家1200米处的超市购物,如图是8点40分时这段时间内他与家的距离随时间变化的图象.根据此图象,请你用简短的语句分别叙述小王在8点40分至8点45分与9点5分至9点25分这两段时间内活动的情况:
8点40分至8点45分: ;9点5分至9点25分: .
14、冬天来临某商店购进一批棉手套,经试销发现,若按每双26元的价格销售,则每月能售出320双;若按每双31元的价格出售,则每月能售出230双,假定每月的销售量y(双)是价格x(元)的一次函数,则该一个函数的表达式为 .
15、某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:①快递车从甲地到乙地的速度为100千米/时;
②快递车从甲地到乙地用了3小时;
③甲、乙两地之间的距离为120千米;
④图中点B的坐标为;
⑤快递车从乙地返回时的速度为90千米/时,
以上5个结论正确的是 .
16、某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km/h,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均每小时减1千米/时.第40h时,测得风速为17km/h,结合风速及时间的图象,回答下列问题:
(1)在y轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当x≥25时,风速y(km/h)
与时间x(h)之间的函数关系式.
(4)若风速达到或超过20km/h,
称为强沙尘暴,则强沙尘暴持续多少时间?
17、某房地产开发公司计划开发A、B两种户型的住房共100套,该公司所筹资金不少于4377万元,但不超过4386万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
A
B
成本(万元/套)
42
45
售价(万元/套)
50
55
(1)该公司对这两种户型住房有哪几种建房方案?
(2)该公司如何建房获得利润最大?
(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?(注:利润=售价-成本)
18、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
(1)甲、乙两地之间的距离为多少千米;
(2)请解释图中点B的实际意义;?
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,
并写出自变量x的取值范围;?
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.
在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列
快车比第一列快车晚出发多少小时?
【中考链接】
19.2018年黑龙江齐齐哈尔17.(3.00分)在平面直角坐标系中,点A(,1)在射线OM上,点B(,3)在射线ON上,以AB为直角边作Rt△ABA1,
以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作
第三个Rt△A1B1A2,…,依次规律,
得到Rt△B2017A2018B2018,则点B2018的纵坐标为 .
20、2018年江苏连云港24.某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块
购买数量不低于5000块
红色地砖
原价销售
以八折销售
蓝色地砖
原价销售
以九折销售
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
21、2018江苏南通25.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500km.
22、2018?怀化20.某学校积极响应怀化市“三城同创”的号召,绿化校园,计划购进A,B两种树苗,共21棵,已知A种树苗每棵90元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.
(1)求y与x的函数表达式,其中0≤x≤21;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
参考答案
1、A 2、C 3、B 4、D 5、20, 6、2 9、C 10、C 11、A 12、B
13、在家中,在购物 14、y=18x+788 15、①②④⑤ 19、32019
7、解:(1)∵BC∥x轴,
∴从第70天开始这颗玉米的高度不变.
答:这颗玉米从栽种起,70天以后停止长高.
(2)设直线AB的解析式为y=kx+b(k≠0),
∵经过点A(0,20),B(25,75),
∴由题意得,
解得,
∴直线AB的解析式为(0当x=70时,( cm).
答:直线AB的解析式为(08、解:(1)根据题意得:y=24x×120+20(20x)×200=1120x+80000.
(2)当y=64320时,有64320=1120x+80000,解得:x=14.
∴要派14名工人去生产甲种产品。
(3)根据题意可得,,
解得:,
∵x取整数,∴x=9,10,11.
又∵y=1120x+80000,k=1120<0,
∴y随x的增大而减小,
∴当x=9时,该工厂获得的利润最大,
∴209=11(名),
所以要派11名工人去生产乙种产品才合适.
15、解:①设快递车从甲地到乙地的速度为x千米/时,则
3(x60)=120,解得x=100,故①正确;
②甲、乙两地之间的距离为:120+3×60=300(km),300÷100=3(h),
故②正确;
③因为120千米是快递车到达乙地后两车之间的距离,不是甲、乙两地之间的距离,故③错误;
④因为快递车到达乙地后缷完物品再另装货物共用45分钟,
所以图中点B的横坐标为,纵坐标为,故④正确;
⑤设快递车从乙地返回时的速度为y千米/时,则,
y=90,故⑤正确.
故答案为;①②④⑤.
16、解:(1)2×4=8,
则8+4×(10-4)=32;
(2)32÷1+25=57小时;
(3)根据图象,设直线CD解析式为y=kx+b,
方法①直线CD经过(25,32)(57,0),
得,解得,∴y=x+57(25≤x≤57);
方法②直线CD经过(25,32)(40,17),
得,解得,∴y=x+57(25≤x≤57);
方法③直线y=32 (x25)×1=x+57(25≤x≤57).
(4)解:方法①(32-20)÷4=3h
25-10=15h
(32-20)÷1=12h
3+15+12=30h
方法②根据图象,设直线AB解析式为y=mx+n,
直线AB经过(4,8)(10,32),
得,解得,∴y=4x8(4≤x≤10);
当y=20时,x+57=20,4x8=20,
解得, x1=37,x2=7,
∴x1 x2=377=30.
答:强沙尘暴持续30小时.
17、解:(1)设公司建A户型x套,则建B户型(100-x)套,
由题意得: 4377≤42x+45(100-x )?≤4386
解得:38≤x≤41????经检验,符合题意。
∵x取整数,∴x=38、39、40、41.
∴该公司有以下四种建房方案:
①A户型:38套,B户型62套;② A户型:39套,B户型61套;
③A户型:40套,B户型60套;④A户型:41套,B户型59套.
(2)∵每套A户型获利:4250=8万元,
每套B户型获利:5545=10万元。
∴每套B户型获利﹥每套A户型获利,方案一获利最大.
即建48套A户型,32套B户型时获利最大。
(3)由题意得:A户型住房的售价提高a万元后:
每套A户型获利(8+a)万元,每套B户型仍获利10万元.
∴当8+a﹤10,即a﹤2时,方案一获利最大;
当8+a=10, 即a=2时,四种方案获利一样多;
当8+a﹥10,即a﹥2时,方案四获利最大.
18、解:(1)900;
(2)图中点B的实际意义是:当慢车行驶4h时,慢车和快车相遇;
(3)由图象可知,慢车12h行驶的路程为900km,所以慢车的速度为;
???????? 当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为,所以快车的速度为150km/h;
(4)根据题意,快车行驶900km到达乙地,
所以快车行驶到达乙地,此时两车
之间的距离为,
所以点C的坐标为(6,450).
? 设线段BC所表示的y与x之间的函数关系式为y=kx+b,
把(4,0),(6,450)代入得
? 解得所以,线段BC所表示的y与x之间的函数关系式为y=225x900
? 自变量x的取值范围是4≤x≤6;
(5)慢车与第一列快车相遇30分钟后与第二列快车相遇,此时,慢车的行驶时间是4.5h.把x=4.5代入y=225x900,得y=112.5,
此时,慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km,所以两列快车出发的间隔时间是,即第二列快车比第一列快车晚出发0.75h。
19、【分析】根据题意,分别找到AB、A1B1、A2B2……及 BA1、B1A2、B2A3……线段长度递增规律即可.
【解答】解:由已知可知
点A、A1、A2、A3……A2018
各点在正比例函数y=的图象上,
点B、B1、B2、B3……B2018
各点在正比例函数y=的图象上,
两个函数相减得到横坐标不变的情况下
两个函数图象上点的纵坐标的差为:①
由已知,Rt△A1B1A2,…,到Rt△B2017A2018B2018 都有一个锐角为30°
∴当A(B)点横坐标为时,由①AB=2,则BA1=2,则点A1横坐标为,B1 点纵坐标为9=32
当A1(B1)点横坐标为3时,由①A1B1=6,则B1A2=6,则点A2横坐标为,B2点纵坐标为27=33
当A2(B2)点横坐标为9时,由①A2B2=18,则B2A3=18,则点A3横坐标为,B3点纵坐标为81=34
依此类推
点B2018的纵坐标为32019
故答案为:32019
【点评】本题是平面直角坐标系规律探究题,考查了含有特殊角的直角三角形各边数量关系,解答时注意数形结合.
20、【分析】(1)根据题意结合表格中数据,购买红色地砖4000块,蓝色地砖6000块,需付款86000元;购买红色地砖10000块,蓝色地砖3500块,需付款99000元,分别得出方程得出答案;
(2)利用已知得出x的取值范围,再利用一次函数增减性得出答案.
【解答】解:(1)设红色地砖每块a元,蓝色地砖每块b元,由题意可得:
,解得:,
答:红色地砖每块8元,蓝色地砖每块10元;
(2)设购置蓝色地砖x块,则购置红色地砖(12000x)块,所需的总费用为y元,
由题意可得:,
解得:x≥4000,
又x≤6000,
所以蓝砖块数x的取值范围:4000≤x≤6000,
当4000≤x<5000时,
y=10x+×0.8(12000﹣x)
=76800+3.6x,
所以x=4000时,y有最小值91200,
当5000≤x≤6000时,y=0.9×10x+8×0.8(1200﹣x)=2.6x+76800,
所以x=5000时,y有最小值89800,
∵89800<91200,
∴购买蓝色地砖5000块,红色地砖7000块,费用最少,最少费用为89800元.
【点评】此题主要考查了一次函数的应用以及二元一次方程组的应用,正确得出函数关系式是解题关键.
21、【分析】(1)由图象可知,两车同时出发.等量关系有两个:
3.6×(慢车的速度+快车的速度)=720,(93.6)×慢车的速度=3.6×快车的速度,设慢车的速度为akm/h,快车的速度为bkm/h,依此列出方程组,求解即可;
(2)点C表示快车到达乙地,然后求出快车行驶完全程的时间从而求出点C的横坐标,再求出相遇后两辆车行驶的路程得到点C的纵坐标,从而得解;
(3)分相遇前相距500km和相遇后相遇500km两种情况求解即可.
【解答】解:(1)设慢车的速度为akm/h,
快车的速度为bkm/h,
根据题意,得,解得,
故答案为80,120;
(2)图中点C的实际意义是:快车到达乙地;
∵快车走完全程所需时间为720÷120=6(h),
∴点C的横坐标为6,
纵坐标为(80+120)×(63.6)=480,
即点C(6,480);
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为500km.
即相遇前:(80+120)x=720500,
解得x=1.1,
相遇后:∵点C(6,480),
∴慢车行驶20km两车之间的距离为500km,
∵慢车行驶20km需要的时间是( h),
∴x=6+0.25=6.25(h),
故x=1.1 h或6.25 h,两车之间的距离为500km.
【点评】本题考查了一次函数的应用,主要利用了路程、时间、速度三者之间的关系,(3)要分相遇前与相遇后两种情况讨论,这也是本题容易出错的地方.
22、【分析】(1)根据购买两种树苗所需费用=A种树苗费用+B种树苗费用,即可解答;
(2)根据购买B种树苗的数量少于A种树苗的数量,列出不等式,确定x的取值范围,再根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
【解答】解:(1)根据题意,得:y=90x+70(21x)=20x+1470,
所以函数解析式为:y=20x+1470;
(2)∵购买B种树苗的数量少于A种树苗的数量,
∴21x解得:x>10.5,
又∵y=20x+1470,且x取整数,
∴当x=11时,y有最小值=1690,
∴使费用最省的方案是购买B种树苗10棵,A种树苗11棵,所需费用为1690元.
第2课时 一次函数的简单应用(2)
【知识清单】
一、一次函数的表达式的应用:
从“数”的方面看当一次函数y=kx+b(k、b为常数,k≠0)的函数值为0(即y=0)时,则自变量x的值,即为方程kx+b=0的解;从“形”的方面看函数图象与x轴交点的横坐标x的值,即为方程kx+b=0的解.
二、由两条相交的函数图象可获取的信息:
1.交点坐标用(x0,y0)表示,当x= x0,两函数值相等;
2.对于同一自变量来说,函数图象在上方,说明函数值大;反之函数值小.
【经典例题】
例题1、小明家与爷爷家相距36km,小明7点从家出发,骑自行车回爷爷家,哥哥有事要处理从家出发比弟弟晚一个小时,乘车沿相同路线回爷爷家,小明和哥哥的行进路程S(km)与时间t(时)的函数图象如图所示,则下列说法中错误的有( )
①小明骑自行车的平均速度是12km/h;②9点之前哥哥的速度比弟弟的慢;③哥哥在距爷爷家12km处追上小明;④哥哥比弟弟提前30分钟到爷爷家.
A.1个 B.2个 C.3个 D.4个
【考点】一次函数图象的应用.
【分析】由图象可知,小明骑完全程用了3小时,而哥哥用了1.5小时,二人的行程都是36千米可根据公式S=tv进行计算平均速度;两个图象的交点表示二人在同一时刻到达相同的位置,由图象可知9:00二人相遇,由此可分析其行程.
【解答】①∵小明到爷爷家用时107=3(小时),行程36千米,
∴v=36÷3=12km/h.
??? 故:①正确.
②∵哥哥到爷爷家用时9.58=1.5(小时),行程36千米,
∴v=36÷1.5=24km/h,24>12 .
????????? ? 故:②错误.
③∵二人在9:00相遇,此时小明已骑车2小时,哥哥出发1小时,
∴哥哥的行程=24×1=24(千米),小明的行程=12×2=24(千米),
∴3624=12,
哥哥在距爷爷家12km处追上小明.
? ? 故:③正确.
?? ④∵哥哥到爷爷家的时间为9.5小时,弟弟到爷爷家的时间为10小时,
? 109.5=0.5(小时),0.5时=30分钟.
即:④正确.
故:选A .
【点评】本题考查了函数图象的意义、性质;认真读图、分析变量t、S的意义及取值是解题的关键,本题考查了一次函数的应用,解决本题的关键是读懂函数图象,获取有效信息.
例题2、一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶60千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图像
【考点】一次函数图象的应用.
【分析】(1)设线段AB的解析式为y=kx+b,将(2,140),(3,0)代入,可求线段AB的解析式,根据线段AB的解析式求A点坐标,得出甲乙两地之间的距离;(2)根据相遇时:快车路程+慢车路程=甲乙两地距离,利用t=甲乙两地距离÷快车速度,求t.
【解答】如图①(1)线段AB所在直线的函数解析式为:y=kx+b,
将(2,140)、(3,0)代入得:
,解得,
所以线段AB所在直线的函数解析式为:y=140x+420,
当x=0时, y=420,
所以甲乙两地之间的距离420千米.
(2)设快车的速度为m千米/时,慢车的速度为n千米/时,
由题意得:
,解得,
所以快车的速度为80千米/时,所以
(3)如图②所示.?
【点评】本题考查了一次函数的运用.关键是通过图象,求出直线解析式,利用直线解析式求A点坐标,得出甲乙两地距离,再根据路程、速度、时间的关系解题.
【夯实基础】
1、均匀地向一个如图所示的容器中注水,最后把容器注满,在注水过程中水面高度h随时间t变化的函数图象大致是( )
2、自来水公司为鼓励居民节约用水,采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水35吨,则应交水费(??? )
?A.68.25元? B.70元??? C.75元?? ?D.84元
3、一种蚊香点燃后,室内药物物浓度y(微克/毫升)与点燃蚊香的时间x(时)之间的函数关系如图所示,则当1≤x≤4时,y的取值范围是( )
?A.? B.??? C.?? ?D.
4、某儿童玩具加工厂的生产流水线每小时可生产1500件产品,生产前没有产品积压,生产2小时后安排工人装箱,若每小时可以装产品2000件,则未装箱的产品数y(件)是时间t(小时)的函数,这个函数的大致图象可能是( )
5、某超市推出免费送物品活动,顾客购买某种物品质量x(kg)与交费y(元)由如图所示的一次函数图象确定,则顾客可以免费领取物品的最最小质量为__20____kg.
6、如图,小明购买一种羽毛球所付款金额y(元)与购买量x(个)之间的函数图象由线段OA和射线AB组成,则一次购买10个羽毛球比分10次购买每次购买1个可节省 .
7、栽种了一颗20cm高的玉米苗,它的生长高度y(厘米)与时间x(天)的关系,并画出如图所示的图象(AB是线段,直线BC平行x轴).
(1)这颗玉米,多少天以后停止长高?
(2)求直线AC的解析式,并求这颗玉米最高长多少厘米?
8、某产品生产车间有工人20名.已知每名工人每天可生产甲种产品24个或乙种产品20个,且每生产一个甲种产品可获得利润120元,每生产一个乙种产品可获得利润200元.在这20名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)请写出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为64320元,要派多少名工人去生产甲种产品?
(3)若生产甲种产品的人数大于生产乙种产品人数的,而小于生产乙种产品人数的,要使获取利润最大,你认为安排多少名工人去生产乙种产品才合适?
【提优特训】
9、某校举行趣味运动会,甲、乙两名学生同时从A地到B地,甲先骑自行车到B地后跑步回A地,乙则是先跑步到B地后骑自行车回A地(骑自行车的速度快于跑步的速度),最后两人恰好同时回到A地.已知甲骑自行车比乙骑自行车的速度快.若学生离A地的距离s与所用时间t的函数关系用图象表示如下(实线表示甲的图象,虚线表示乙的图象),则正确的是( )
10、某村办工厂今年前5个月生产某种产品的总量y(件)关于时间x(月)的函数图象如图所示,则该厂对这种产品来说( )
A、1月至2月每月生产总量平稳增加,3,4,5三个月每个月的产量不变
B、1月至2月每月生产总量平均增加,3,4,5三个月每个月的产量不变
C、1月至2月只有原来生产的产品,3,4,5三个月每个月的产量不变
D、1月至2月每月生产总量不变,3,4,5三个月每月生产总量平稳增加
11、如图,在矩形ABCD中,AB=8,BC=6,点P从起点B出发,沿BC、CD逆时针方向向终点D匀速运动.设点P所走过路程为x,则线段AP、AD与矩形的边所围成的图形面积为y,则下列图象中能大致反映y与x函数关系的是( )
12、如图,平面直角坐标系xOy中,点B的坐标为(10,5),BA⊥y轴,垂足为A,点Q从原点O出发向x轴正方向运动,同时,点P从点B出发向点A运动,当点P到达点A时,点P、Q同时停止运动,若点Q与点P的速度之比为2︰3,则下列说法正确的是( )
A.线段PQ始终经过点(2,4) B.线段PQ始终经过点(4,2)
C.线段PQ始终经过点(3,2) D.线段PQ不可能始终经过某一定点
13、星期日上午8点30分李峰从家中出发骑自行车到距家1200米处的超市购物,如图是8点40分时这段时间内他与家的距离随时间变化的图象.根据此图象,请你用简短的语句分别叙述小王在8点40分至8点45分与9点5分至9点25分这两段时间内活动的情况:
8点40分至8点45分: ;9点5分至9点25分: .
14、冬天来临某商店购进一批棉手套,经试销发现,若按每双26元的价格销售,则每月能售出320双;若按每双31元的价格出售,则每月能售出230双,假定每月的销售量y(双)是价格x(元)的一次函数,则该一个函数的表达式为 .
15、某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:①快递车从甲地到乙地的速度为100千米/时;
②快递车从甲地到乙地用了3小时;
③甲、乙两地之间的距离为120千米;
④图中点B的坐标为;
⑤快递车从乙地返回时的速度为90千米/时,
以上5个结论正确的是 .
16、某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km/h,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均每小时减1千米/时.第40h时,测得风速为17km/h,结合风速及时间的图象,回答下列问题:
(1)在y轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当x≥25时,风速y(km/h)
与时间x(h)之间的函数关系式.
(4)若风速达到或超过20km/h,
称为强沙尘暴,则强沙尘暴持续多少时间?
17、某房地产开发公司计划开发A、B两种户型的住房共100套,该公司所筹资金不少于4377万元,但不超过4386万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
A
B
成本(万元/套)
42
45
售价(万元/套)
50
55
(1)该公司对这两种户型住房有哪几种建房方案?
(2)该公司如何建房获得利润最大?
(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?(注:利润=售价-成本)
18、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
(1)甲、乙两地之间的距离为多少千米;
(2)请解释图中点B的实际意义;?
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,
并写出自变量x的取值范围;?
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.
在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列
快车比第一列快车晚出发多少小时?
【中考链接】
19.2018年黑龙江齐齐哈尔17.(3.00分)在平面直角坐标系中,点A(,1)在射线OM上,点B(,3)在射线ON上,以AB为直角边作Rt△ABA1,
以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作
第三个Rt△A1B1A2,…,依次规律,
得到Rt△B2017A2018B2018,则点B2018的纵坐标为 .
20、2018年江苏连云港24.某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块
购买数量不低于5000块
红色地砖
原价销售
以八折销售
蓝色地砖
原价销售
以九折销售
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
21、2018江苏南通25.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500km.
22、2018?怀化20.某学校积极响应怀化市“三城同创”的号召,绿化校园,计划购进A,B两种树苗,共21棵,已知A种树苗每棵90元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.
(1)求y与x的函数表达式,其中0≤x≤21;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
参考答案
1、A 2、C 3、B 4、D 5、20, 6、2 9、C 10、C 11、A 12、B
13、在家中,在购物 14、y=18x+788 15、①②④⑤ 19、32019
7、解:(1)∵BC∥x轴,
∴从第70天开始这颗玉米的高度不变.
答:这颗玉米从栽种起,70天以后停止长高.
(2)设直线AB的解析式为y=kx+b(k≠0),
∵经过点A(0,20),B(25,75),
∴由题意得,
解得,
∴直线AB的解析式为(0
答:直线AB的解析式为(0
(2)当y=64320时,有64320=1120x+80000,解得:x=14.
∴要派14名工人去生产甲种产品。
(3)根据题意可得,,
解得:,
∵x取整数,∴x=9,10,11.
又∵y=1120x+80000,k=1120<0,
∴y随x的增大而减小,
∴当x=9时,该工厂获得的利润最大,
∴209=11(名),
所以要派11名工人去生产乙种产品才合适.
15、解:①设快递车从甲地到乙地的速度为x千米/时,则
3(x60)=120,解得x=100,故①正确;
②甲、乙两地之间的距离为:120+3×60=300(km),300÷100=3(h),
故②正确;
③因为120千米是快递车到达乙地后两车之间的距离,不是甲、乙两地之间的距离,故③错误;
④因为快递车到达乙地后缷完物品再另装货物共用45分钟,
所以图中点B的横坐标为,纵坐标为,故④正确;
⑤设快递车从乙地返回时的速度为y千米/时,则,
y=90,故⑤正确.
故答案为;①②④⑤.
16、解:(1)2×4=8,
则8+4×(10-4)=32;
(2)32÷1+25=57小时;
(3)根据图象,设直线CD解析式为y=kx+b,
方法①直线CD经过(25,32)(57,0),
得,解得,∴y=x+57(25≤x≤57);
方法②直线CD经过(25,32)(40,17),
得,解得,∴y=x+57(25≤x≤57);
方法③直线y=32 (x25)×1=x+57(25≤x≤57).
(4)解:方法①(32-20)÷4=3h
25-10=15h
(32-20)÷1=12h
3+15+12=30h
方法②根据图象,设直线AB解析式为y=mx+n,
直线AB经过(4,8)(10,32),
得,解得,∴y=4x8(4≤x≤10);
当y=20时,x+57=20,4x8=20,
解得, x1=37,x2=7,
∴x1 x2=377=30.
答:强沙尘暴持续30小时.
17、解:(1)设公司建A户型x套,则建B户型(100-x)套,
由题意得: 4377≤42x+45(100-x )?≤4386
解得:38≤x≤41????经检验,符合题意。
∵x取整数,∴x=38、39、40、41.
∴该公司有以下四种建房方案:
①A户型:38套,B户型62套;② A户型:39套,B户型61套;
③A户型:40套,B户型60套;④A户型:41套,B户型59套.
(2)∵每套A户型获利:4250=8万元,
每套B户型获利:5545=10万元。
∴每套B户型获利﹥每套A户型获利,方案一获利最大.
即建48套A户型,32套B户型时获利最大。
(3)由题意得:A户型住房的售价提高a万元后:
每套A户型获利(8+a)万元,每套B户型仍获利10万元.
∴当8+a﹤10,即a﹤2时,方案一获利最大;
当8+a=10, 即a=2时,四种方案获利一样多;
当8+a﹥10,即a﹥2时,方案四获利最大.
18、解:(1)900;
(2)图中点B的实际意义是:当慢车行驶4h时,慢车和快车相遇;
(3)由图象可知,慢车12h行驶的路程为900km,所以慢车的速度为;
???????? 当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为,所以快车的速度为150km/h;
(4)根据题意,快车行驶900km到达乙地,
所以快车行驶到达乙地,此时两车
之间的距离为,
所以点C的坐标为(6,450).
? 设线段BC所表示的y与x之间的函数关系式为y=kx+b,
把(4,0),(6,450)代入得
? 解得所以,线段BC所表示的y与x之间的函数关系式为y=225x900
? 自变量x的取值范围是4≤x≤6;
(5)慢车与第一列快车相遇30分钟后与第二列快车相遇,此时,慢车的行驶时间是4.5h.把x=4.5代入y=225x900,得y=112.5,
此时,慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km,所以两列快车出发的间隔时间是,即第二列快车比第一列快车晚出发0.75h。
19、【分析】根据题意,分别找到AB、A1B1、A2B2……及 BA1、B1A2、B2A3……线段长度递增规律即可.
【解答】解:由已知可知
点A、A1、A2、A3……A2018
各点在正比例函数y=的图象上,
点B、B1、B2、B3……B2018
各点在正比例函数y=的图象上,
两个函数相减得到横坐标不变的情况下
两个函数图象上点的纵坐标的差为:①
由已知,Rt△A1B1A2,…,到Rt△B2017A2018B2018 都有一个锐角为30°
∴当A(B)点横坐标为时,由①AB=2,则BA1=2,则点A1横坐标为,B1 点纵坐标为9=32
当A1(B1)点横坐标为3时,由①A1B1=6,则B1A2=6,则点A2横坐标为,B2点纵坐标为27=33
当A2(B2)点横坐标为9时,由①A2B2=18,则B2A3=18,则点A3横坐标为,B3点纵坐标为81=34
依此类推
点B2018的纵坐标为32019
故答案为:32019
【点评】本题是平面直角坐标系规律探究题,考查了含有特殊角的直角三角形各边数量关系,解答时注意数形结合.
20、【分析】(1)根据题意结合表格中数据,购买红色地砖4000块,蓝色地砖6000块,需付款86000元;购买红色地砖10000块,蓝色地砖3500块,需付款99000元,分别得出方程得出答案;
(2)利用已知得出x的取值范围,再利用一次函数增减性得出答案.
【解答】解:(1)设红色地砖每块a元,蓝色地砖每块b元,由题意可得:
,解得:,
答:红色地砖每块8元,蓝色地砖每块10元;
(2)设购置蓝色地砖x块,则购置红色地砖(12000x)块,所需的总费用为y元,
由题意可得:,
解得:x≥4000,
又x≤6000,
所以蓝砖块数x的取值范围:4000≤x≤6000,
当4000≤x<5000时,
y=10x+×0.8(12000﹣x)
=76800+3.6x,
所以x=4000时,y有最小值91200,
当5000≤x≤6000时,y=0.9×10x+8×0.8(1200﹣x)=2.6x+76800,
所以x=5000时,y有最小值89800,
∵89800<91200,
∴购买蓝色地砖5000块,红色地砖7000块,费用最少,最少费用为89800元.
【点评】此题主要考查了一次函数的应用以及二元一次方程组的应用,正确得出函数关系式是解题关键.
21、【分析】(1)由图象可知,两车同时出发.等量关系有两个:
3.6×(慢车的速度+快车的速度)=720,(93.6)×慢车的速度=3.6×快车的速度,设慢车的速度为akm/h,快车的速度为bkm/h,依此列出方程组,求解即可;
(2)点C表示快车到达乙地,然后求出快车行驶完全程的时间从而求出点C的横坐标,再求出相遇后两辆车行驶的路程得到点C的纵坐标,从而得解;
(3)分相遇前相距500km和相遇后相遇500km两种情况求解即可.
【解答】解:(1)设慢车的速度为akm/h,
快车的速度为bkm/h,
根据题意,得,解得,
故答案为80,120;
(2)图中点C的实际意义是:快车到达乙地;
∵快车走完全程所需时间为720÷120=6(h),
∴点C的横坐标为6,
纵坐标为(80+120)×(63.6)=480,
即点C(6,480);
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为500km.
即相遇前:(80+120)x=720500,
解得x=1.1,
相遇后:∵点C(6,480),
∴慢车行驶20km两车之间的距离为500km,
∵慢车行驶20km需要的时间是( h),
∴x=6+0.25=6.25(h),
故x=1.1 h或6.25 h,两车之间的距离为500km.
【点评】本题考查了一次函数的应用,主要利用了路程、时间、速度三者之间的关系,(3)要分相遇前与相遇后两种情况讨论,这也是本题容易出错的地方.
22、【分析】(1)根据购买两种树苗所需费用=A种树苗费用+B种树苗费用,即可解答;
(2)根据购买B种树苗的数量少于A种树苗的数量,列出不等式,确定x的取值范围,再根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
【解答】解:(1)根据题意,得:y=90x+70(21x)=20x+1470,
所以函数解析式为:y=20x+1470;
(2)∵购买B种树苗的数量少于A种树苗的数量,
∴21x
又∵y=20x+1470,且x取整数,
∴当x=11时,y有最小值=1690,
∴使费用最省的方案是购买B种树苗10棵,A种树苗11棵,所需费用为1690元.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
