2018-2019学年度第一学期浙教版九年级数学第三章圆的基本性质单元检测试卷(含答案)
文档属性
| 名称 | 2018-2019学年度第一学期浙教版九年级数学第三章圆的基本性质单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 154.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-18 21:07:55 | ||
图片预览


文档简介
2018-2019学年度第一学期浙教版九年级数学上册
第三章 圆的基本性质 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,的直径与弦交于点,,,,则的度数是( )
A. B. C. D.
?2.,是圆的两条平行弦,那么由,,,四点构成的四边形一定不是( )
A.矩形 B.正方形 C.等腰梯形 D.直角梯形
?3.如图,是的直径,、是上的点,,连接,,若等于,则等于( )
A. B. C. D.
?4.若的半径为,点到圆心的距离不大于,则点
A.在内 B.在外
C.不在内 D.不在外
?5.下列命题正确的有( )
A.在同圆或等圆中,等弦所对的弧相等
B.圆的两条不是直径的相交弦,不能互相平分
C.正多边形的中心是它的对称中心
D.各边相等的圆外切多边形是正多边形?
6.在半径为的圆中,圆心角所对的弧长为( )
A. B. C. D.
?7.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为的“等边扇形”的面积为( )
A. B. C. D.
8.下列图形一定有外接圆的是( )
A.三角形 B.平行四边形
C.梯形 D.菱形
?9.若的半径为,点到圆心的距离为,那么点与的位置关系是( )
A.点在外 B.点在上
C.点在?内 D.不能确定
?10.的直径为,,则点与的位置关系是( )
A.在内 B.在上
C.在外 D.无法确定
二、填空题(共 8 小题 ,每小题 3 分 ,共 24 分 )
?11.如图,已知是圆内接三角形,若,则________度.
12.如图,照相时为了把近处的较高物体照下来,常常保持镜头中心不动,使相机旋转一定的角度,若点从水平位置顺时针旋转了,那么点从水平位置顺时针旋转了________度.
?
13.如图,在中,,将在平面内绕点旋转到的位置,使,则旋转角的度数为________.
?14.如图,中,,,将绕点逆时针旋转到,那么扫过的区域(图中阴影部分)的面积是________.
15.如图,一种电子游戏,电子屏幕上有一正六边形,点沿直线从右向左移动,当出现点与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线上会发出警报的点的个数为________.
?
16.如图,的半径为,弦的长为,点在线段(包括端点,)上移动,则的取值范围是________.
?17.如图,已知反比例函数的图象经过点,若在轴上存在点,使得线段绕点逆时针旋转后,点仍落在反比例函数图象上,则点的坐标为________.
?
18.如图,是的直径,是上的一点,若,,于点,则的长为________.
三、解答题(共 8 小题 ,共 66 分 )
19.(8分) 如图,已知是的弦,,,是弦上任意一点(不与点、重合),连接并延长
交于点,连接.
弦________(结果保留根号);
当时,求的度数.
?
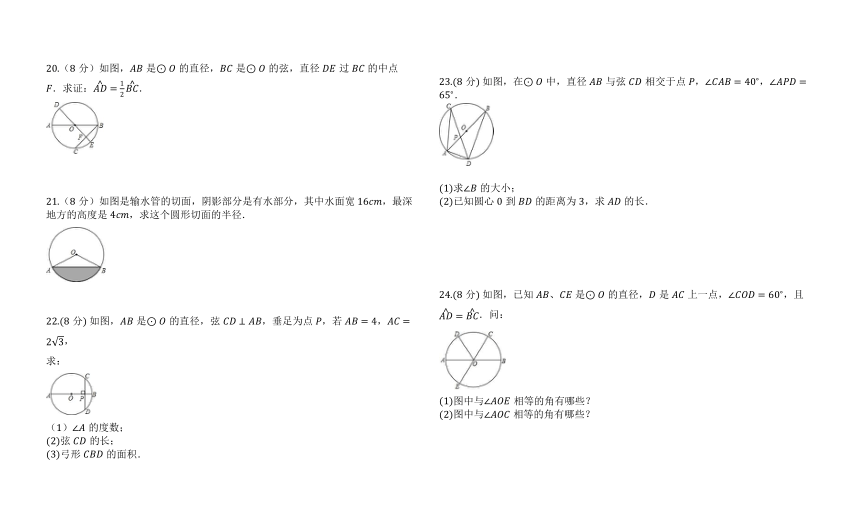
20.(8分)如图,是的直径,是的弦,直径过的中点.求证:.
?
21.(8分)如图是输水管的切面,阴影部分是有水部分,其中水面宽?,最深地方的高度是,求这个圆形切面的半径.
?
22.(8分) 如图,是的直径,弦,垂足为点,若,,
求:
(1)的度数;?
弦的长;?
弓形的面积.
?
23.(8分) 如图,在中,直径与弦相交于点,,.
求的大小;
已知圆心到的距离为,求的长.
?
24.(8分) 如图,已知、是的直径,是上一点,,且.问:
图中与相等的角有哪些?
图中与相等的角有哪些?
?
25.(8分) 如图,在中,点是内心,延长交的外接圆于点,连接、、,且.
求证:是等边三角形.
若,猜想四边形是怎样的四边形,并证明你的猜想.
?
26.(10分) 如图,已知是的直径,弦,垂足为.
求证:;
若过的直线与弦(不含端点)相交于点,与相交于点,求证:.
答案
1.C
2.D
3.D
4.D
5.B
6.D
7.C
8.A
9.C
10.C
11.
12.
13.
14.
15.
16.
17.或
18.
19.解:如图,过作于,
∴是的中点,
?在中,,,
∴,
∴,
∴;
解法一:∵,.
∴.?…
又∵,,,
∴,,…
∴.…
解法二:如图,连接.
∵,,
∴,,
∴.?…
又∵,,
∴,…
∴(同弧所对的圆周角等于它所对圆心角的一半).??…
20.证明:连接,
∵,为中点,
∴,
∵过,
∴弧弧弧,
∵,
∴弧弧,
∴.
21.这个圆形切面的半径是.
22.解:
连接,,
∵是的直径,
∴;
∴√
∴
∴;∵,,
∴,
;连接,,
∵,
∴,,
∴,
∴,
∵,
∴,
∴弓形的面积.
23.解:∵(同弧所对的圆周角相等),,
∴;
又∵,
∴;
∴在中,
∴;过点作于点,则.
∵是直径,
∴(直径所对的圆周角是直角);
∴;
又∵是的中点,
∴是的中位线,
∴.
24.解:∵,
∴,
∵,,
∴,
∵,
∴与相等的角有:,,;∵,
∴,
∴与相等的角有:,,.
25.四边形是菱形,
证明:∵,
由得,
∵,
同得,可推出,
∴是等边三角形,
∴,
由得是等边三角形,
∴,
∴,
∴四边形是菱形.
26.证明:连接,
∵是的直径,
∴,
而,
∴,
∴,
即;
连接,易证,
∴,
∴;
(也可连接,证)
第三章 圆的基本性质 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,的直径与弦交于点,,,,则的度数是( )
A. B. C. D.
?2.,是圆的两条平行弦,那么由,,,四点构成的四边形一定不是( )
A.矩形 B.正方形 C.等腰梯形 D.直角梯形
?3.如图,是的直径,、是上的点,,连接,,若等于,则等于( )
A. B. C. D.
?4.若的半径为,点到圆心的距离不大于,则点
A.在内 B.在外
C.不在内 D.不在外
?5.下列命题正确的有( )
A.在同圆或等圆中,等弦所对的弧相等
B.圆的两条不是直径的相交弦,不能互相平分
C.正多边形的中心是它的对称中心
D.各边相等的圆外切多边形是正多边形?
6.在半径为的圆中,圆心角所对的弧长为( )
A. B. C. D.
?7.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为的“等边扇形”的面积为( )
A. B. C. D.
8.下列图形一定有外接圆的是( )
A.三角形 B.平行四边形
C.梯形 D.菱形
?9.若的半径为,点到圆心的距离为,那么点与的位置关系是( )
A.点在外 B.点在上
C.点在?内 D.不能确定
?10.的直径为,,则点与的位置关系是( )
A.在内 B.在上
C.在外 D.无法确定
二、填空题(共 8 小题 ,每小题 3 分 ,共 24 分 )
?11.如图,已知是圆内接三角形,若,则________度.
12.如图,照相时为了把近处的较高物体照下来,常常保持镜头中心不动,使相机旋转一定的角度,若点从水平位置顺时针旋转了,那么点从水平位置顺时针旋转了________度.
?
13.如图,在中,,将在平面内绕点旋转到的位置,使,则旋转角的度数为________.
?14.如图,中,,,将绕点逆时针旋转到,那么扫过的区域(图中阴影部分)的面积是________.
15.如图,一种电子游戏,电子屏幕上有一正六边形,点沿直线从右向左移动,当出现点与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线上会发出警报的点的个数为________.
?
16.如图,的半径为,弦的长为,点在线段(包括端点,)上移动,则的取值范围是________.
?17.如图,已知反比例函数的图象经过点,若在轴上存在点,使得线段绕点逆时针旋转后,点仍落在反比例函数图象上,则点的坐标为________.
?
18.如图,是的直径,是上的一点,若,,于点,则的长为________.
三、解答题(共 8 小题 ,共 66 分 )
19.(8分) 如图,已知是的弦,,,是弦上任意一点(不与点、重合),连接并延长
交于点,连接.
弦________(结果保留根号);
当时,求的度数.
?
20.(8分)如图,是的直径,是的弦,直径过的中点.求证:.
?
21.(8分)如图是输水管的切面,阴影部分是有水部分,其中水面宽?,最深地方的高度是,求这个圆形切面的半径.
?
22.(8分) 如图,是的直径,弦,垂足为点,若,,
求:
(1)的度数;?
弦的长;?
弓形的面积.
?
23.(8分) 如图,在中,直径与弦相交于点,,.
求的大小;
已知圆心到的距离为,求的长.
?
24.(8分) 如图,已知、是的直径,是上一点,,且.问:
图中与相等的角有哪些?
图中与相等的角有哪些?
?
25.(8分) 如图,在中,点是内心,延长交的外接圆于点,连接、、,且.
求证:是等边三角形.
若,猜想四边形是怎样的四边形,并证明你的猜想.
?
26.(10分) 如图,已知是的直径,弦,垂足为.
求证:;
若过的直线与弦(不含端点)相交于点,与相交于点,求证:.
答案
1.C
2.D
3.D
4.D
5.B
6.D
7.C
8.A
9.C
10.C
11.
12.
13.
14.
15.
16.
17.或
18.
19.解:如图,过作于,
∴是的中点,
?在中,,,
∴,
∴,
∴;
解法一:∵,.
∴.?…
又∵,,,
∴,,…
∴.…
解法二:如图,连接.
∵,,
∴,,
∴.?…
又∵,,
∴,…
∴(同弧所对的圆周角等于它所对圆心角的一半).??…
20.证明:连接,
∵,为中点,
∴,
∵过,
∴弧弧弧,
∵,
∴弧弧,
∴.
21.这个圆形切面的半径是.
22.解:
连接,,
∵是的直径,
∴;
∴√
∴
∴;∵,,
∴,
;连接,,
∵,
∴,,
∴,
∴,
∵,
∴,
∴弓形的面积.
23.解:∵(同弧所对的圆周角相等),,
∴;
又∵,
∴;
∴在中,
∴;过点作于点,则.
∵是直径,
∴(直径所对的圆周角是直角);
∴;
又∵是的中点,
∴是的中位线,
∴.
24.解:∵,
∴,
∵,,
∴,
∵,
∴与相等的角有:,,;∵,
∴,
∴与相等的角有:,,.
25.四边形是菱形,
证明:∵,
由得,
∵,
同得,可推出,
∴是等边三角形,
∴,
由得是等边三角形,
∴,
∴,
∴四边形是菱形.
26.证明:连接,
∵是的直径,
∴,
而,
∴,
∴,
即;
连接,易证,
∴,
∴;
(也可连接,证)
同课章节目录
