【期末专题复习】浙教版九年级数学上册《第三章圆的基本性质》单元检测试卷(含答案)
文档属性
| 名称 | 【期末专题复习】浙教版九年级数学上册《第三章圆的基本性质》单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-24 19:23:49 | ||
图片预览


文档简介
【期末专题复习】浙教版九年级数学上册 第三章 圆的基本性质 单元检测试卷
一、单选题(共10题;共30分)
1.已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是(?? )
A.?点P在⊙O内??????????????????????/B.?点P在⊙O上??????????????????????/C.?点P在⊙O外??????????????????????/D.?无法判断
2.如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是(?? ) /
A.?42°???????????????????????????????????????B.?21°???????????????????????????????????????C.?84°???????????????????????????????????????D.?60°
3.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为(?? ) /
A.?3?????????????????????????????????????????/B.?2.5?????????????????????????????????????????/C.?4?????????????????????????????????????????/D.?3.5
4.已知AB=7cm,则过点A,B,且半径为3cm的圆有( )
A.?0个????????????????????????????????????/B.?1个????????????????????????????????????/C.?2个??????????????????????????????????????/D.?无数个
5.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,CM切⊙O于点C,∠BCM=60°,则∠B的正切值是( )
A.?
1
2
???????????????????????????????????????/B.?
3
3
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
3
6.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是(??) /
A.?25°???????????????????????????????????????B.?30°???????????????????????????????????????C.?35°???????????????????????????????????????D.?40°
7.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( ) ?/
A.?2π????????????????????????????????????B.?4π????????????????????????????????????C.?5π??? ????????????????????????????????????D.?6π
8.如图,⊙O是△ABC的外接圆,已知∠ABO=30o,则∠ACB的大小为?????????( ??) /
A.?60o??????????????????????????????????????/B.?30o??????????????????????????????????????/C.?45o??????????????????????????????????????/D.?50o
9.如图,将△ABC绕点C顺时针方向旋转40°,得△A′CB′,若AC⊥A′B′,则∠BAC等于(?? ) /
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
10.如图,点C是⊙O上一点,⊙O的半径为 2
2
,D、E分别是弦AC、BC上一动点,且OD=OE=
2
,则AB的最大值为(?? ) /
A.?2
6
?????????????????????????????????????/B.?2
3
?????????????????????????????????????/C.?2
2
?????????????????????????????????????/D.?4
2
二、填空题(共10题;共30分)
11.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的直径________cm.
12.如图所示,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积是________./
13.如图:在△ABC中,∠A、∠B的对边分别为a、b,且∠C=90°,分别以AC、BC为直径作半圆,则图中阴影部分的面积为________?
/
14.在矩形ABCD中,AB=4,BC=6,动点P为矩形边上的一点,点P沿着B﹣C的路径运动(含点B和点C),则△ADP的外接圆的圆心O的运动路径长是________. //
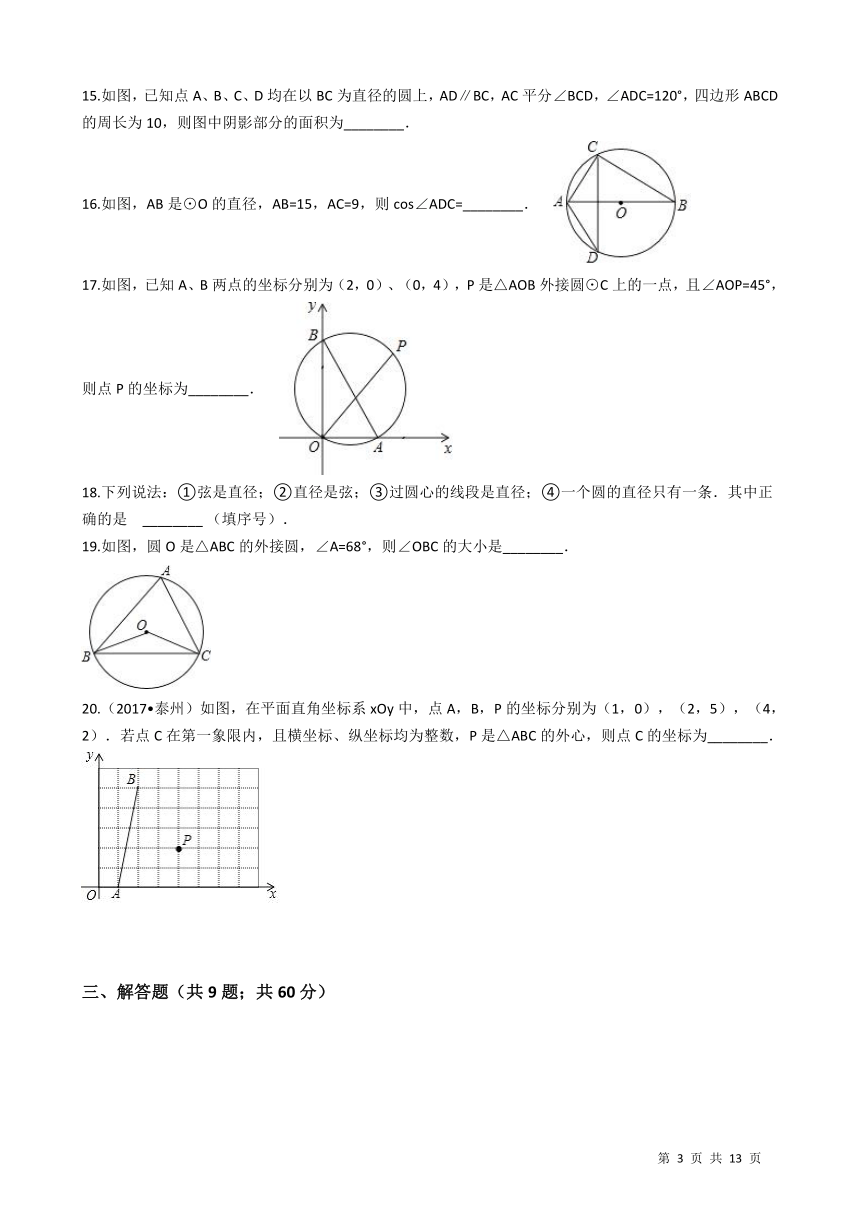
15.如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为________.
16.如图,AB是⊙O的直径,AB=15,AC=9,则cos∠ADC=________. /
17.如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为________. /
18.下列说法:①弦是直径;②直径是弦;③过圆心的线段是直径;④一个圆的直径只有一条.其中正确的是 ________?(填序号).
19.如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是________. /
20.(2017?泰州)如图,在平面直角坐标系xOy中,点A,B,P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为________. /
三、解答题(共9题;共60分)
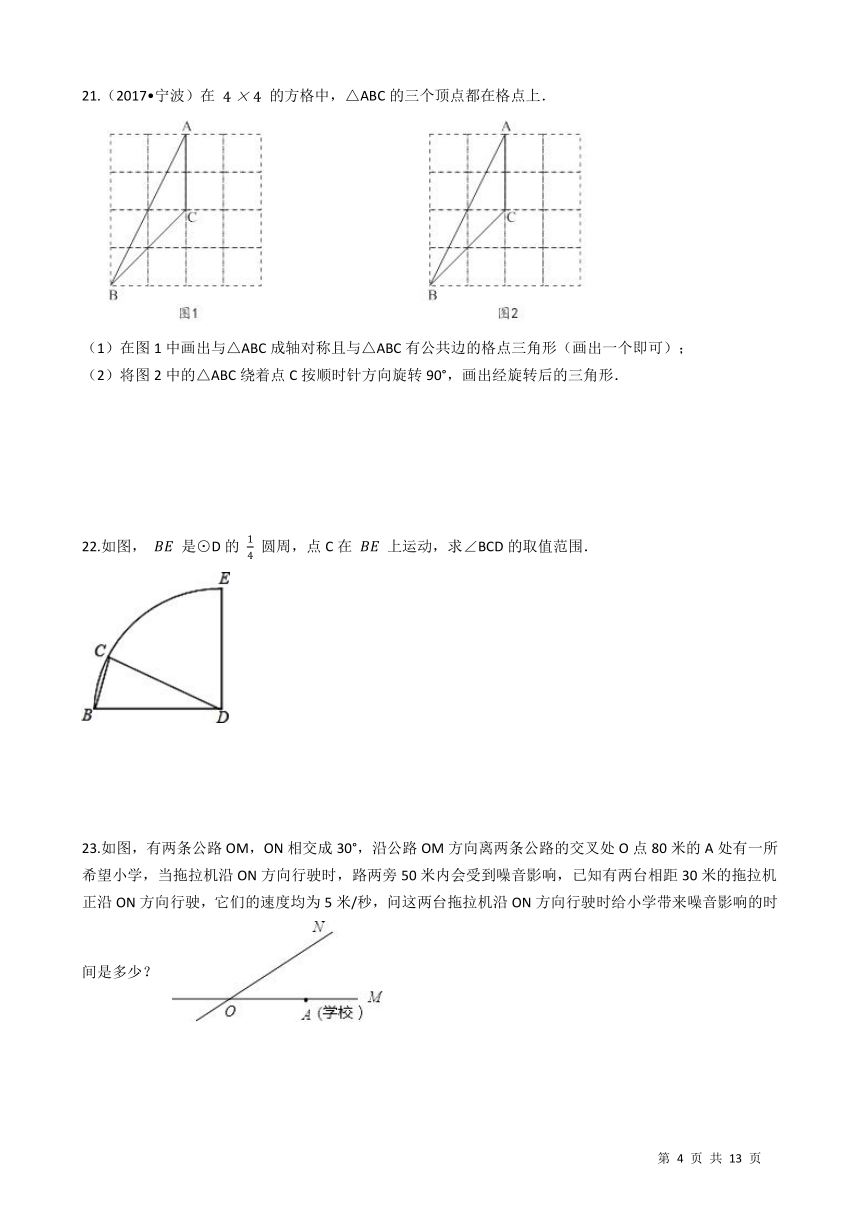
21.(2017?宁波)在 4×4 的方格中,△ABC的三个顶点都在格点上. /
(1)在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);
(2)将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.
22.如图,
????
是⊙D的
1
4
圆周,点C在
????
上运动,求∠BCD的取值范围.
/
23.如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少? /
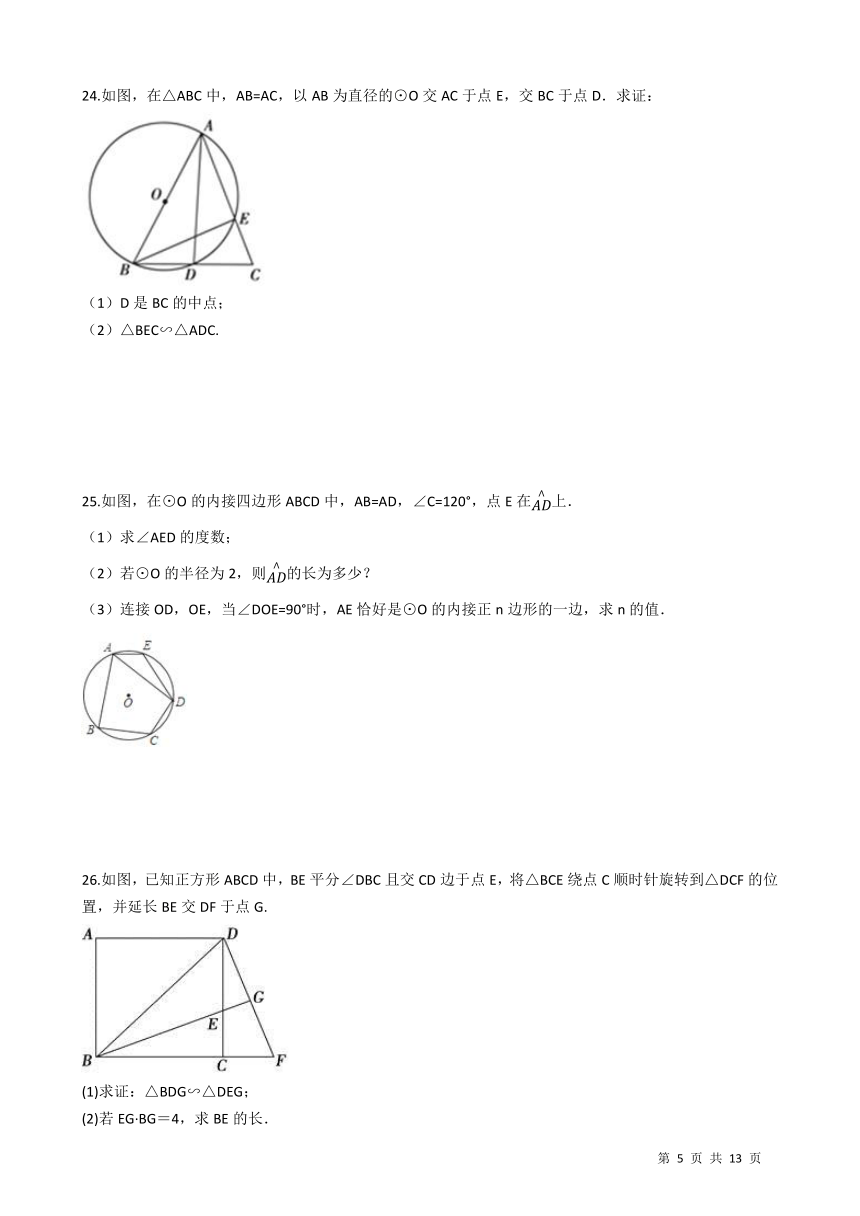
24.如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证: / (1)D是BC的中点; (2)△BEC∽△ADC.
25.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在
????
∧
上. (1)求∠AED的度数; (2)若⊙O的半径为2,则
????
∧
的长为多少? (3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值. /
26.如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G. / (1)求证:△BDG∽△DEG; (2)若EG·BG=4,求BE的长.
27.△ABC和△ECD都是等边三角形 / (1)如图1,若B、C、D三点在一条直线上,求证:BE=AD; (2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
28.如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF. / (1)求证:△ADE≌△ABF; (2)填空:△ABF可以由△ADE绕旋转中心 ?????点,按顺时针方向旋转 ???度得到; (3)若BC=8,DE=6,求△AEF的面积.
29.如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC. (1)求证:∠ACF=∠ADB; (2)若点A到BD的距离为m,BF+CF=n,求线段CD的长; (3)当⊙P的大小发生变化而其他条件不变时,
????
????
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由. /
答案解析部分
一、单选题
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】A
9.【答案】A
10.【答案】A
二、填空题
11.【答案】10
12.【答案】4-
8
9
π
13.【答案】
1
8
π
a
2
+
b
2
?
1
2
ab
14.【答案】
9
4
15.【答案】
3
16.【答案】
4
5
17.【答案】(3,3)
18.【答案】②
19.【答案】22°
20.【答案】(7,4)或(6,5)或(1,4)
三、解答题
21.【答案】(1)解:画出下列其中一个即可. / (2)解: /
22.【答案】解:∵
????
是⊙D的
1
4
圆周,
∴∠BDE=
1
4
×360°=90°,
∵DB=DC,
∴∠B=∠BCD,
∴∠BCD=
1
2
(180°﹣∠BDC)=90°﹣
1
2
∠BDC,
而0≤∠BDC≤90°,
∴45°≤∠BCD≤90°
23.【答案】解:如图, / 过点A作AC⊥ON, ∵∠MON=30°,OA=80米, ∴AC=40米, 当第一台拖拉机到B点时对学校产生噪音影响,此时AB=50, 由勾股定理得:BC=30, 第一台拖拉机到D点时噪音消失, 所以CD=30. 由于两台拖拉机相距30米,则第一台到D点时第二台在C点,还须前行30米后才对学校没有噪音影响. 所以影响时间应是:90÷5=18秒. 答:这两台拖拉机沿ON方向行驶给小学带来噪音影响的时间是18秒
24.【答案】解:(1)证明: ∵AB为⊙O的直径, ∴∠BDA=90°, ∴AD⊥BC. ∵AB=AC. ∴BD=CD, ∴D是BC的中点; (2)∵AB=AC, ∴∠C=∠ABD, ∵AB为⊙O的直径, ∴∠ADB=∠BEC=90°, ∴△BEC∽△ADC;
25.【答案】解:(1)连接BD,如图1所示: ∵四边形ABCD是⊙O的内接四边形, ∴∠BAD+∠C=180°, ∵∠C=120°, ∴∠BAD=60°, ∵AB=AD, ∴△ABD是等边三角形, ∴∠ABD=60°, ∵四边形ABDE是⊙O的内接四边形,∴∠AED+∠ABD=180°, ∴∠AED=120°; (2)∵∠AOD=2∠ABD=120°, ∴
????
∧
的长=
120×π×2
180
=
4π
3
; (3)连接OA,如图2所示: ∵∠ABD=60°, ∴∠AOD=2∠ABD=120°, ∵∠DOE=90°, ∴∠AOE=∠AOD﹣∠DOE=30°, ∴n=
360°
30°
=12. /
26.【答案】(1)证明:∵将△BCE绕点C顺时针旋转到△DCF的位置,∴△BCE≌△DCF, ∴∠FDC=∠EBC,∵BE平分∠DBC, ∴∠DBE=∠EBC,∴∠FDC=∠EBD, ∵∠DGE=∠DGE,∴△BDG∽△DEG. (2)解:∵△BCE≌△DCF, ∴∠F=∠BEC,∠EBC=∠FDC, ∵四边形ABCD是正方形, ∴∠DCB=90°,∠DBC=∠BDC=45°, ∵BE平分∠DBC, ∴∠DBE=∠EBC=22.5°=∠FDC, ∴∠BDF=45°+22.5°=67.5°, ∠F=90°-22.5°=67.5°=∠BDF, ∴BD=BF,∵△BCE≌△DCF, ∴∠F=∠BEC=67.5°=∠DEG, ∴∠DGB=180°-22.5°-67.5°=90°, 即BG⊥DF,∵BD=BF,∴DF=2DG, ∵△BDG∽△DEG,BG·EG=4, ∴
????
????
=
????
????
, ∴BG·EG=DG·DG=4, ∴DG=2,∴BE=DF=2DG=4.
27.【答案】解:(1)∵△ABC和△ECD都是等边三角形,∴AC=BC,EC=DC,∠ACB=∠ECD=60°. ∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE. ∴△ACD≌△BCE. ∴AD=BE. (2)BC垂直平分DE,理由如下: 如图, / 延长BC交DE于M, ∵∠ACB=60°,∠ACE=90°,∴∠ECM=180°-∠ACB-∠ACE=30°. ∵∠DCM=∠ECD-∠ECM=30°,∴∠ECM=∠DCM. ∵△ECD是等边三角形,∴CM垂直平分DE,即BC垂直平分DE.
28.【答案】解;(1)∵四边形ABCD是正方形, ∴AD=AB,∠D=∠ABC=90°, ∴∠ABF=90°, 在△ADE和△ABF中,
????=????
∠??????=∠??????
????=????
, ∴△ADE≌△ABF(SAS) (2)A、90; (3)∵在正方形ABCD中,AD=BC=8,DE=6,∠D=90°, ∴AE=
??
??
2
+??
??
2
=10, ∵△ABF可以由△ADE绕A点顺时针方向旋转90°得到, ∴AE=AF,∠EAF=90°, ∴△AEF的面积=
1
2
AE2=
1
2
×100=50(平方单位).
29.【答案】(1)证明:连接AB, ∵OP⊥BC, ∴BO=CO, ∴AB=AC, 又∵AC=AD, ∴AB=AD, ∴∠ABD=∠ADB, 又∵∠ABD=∠ACF, ∴∠ACF=∠ADB.???? (2)解:过点A作AM⊥CF交CF的延长线于M,过点A作AN⊥BF于N,连接AF, 则AN=m, ∴∠ANB=∠AMC=90°, 在△ABN和△ACM中 ,
∠??????=∠??????
∠??????=∠??????
????=????
∴Rt△ABN≌Rt△ACM(AAS) ∴BN=CM,AN=AM, 又∵∠ANF=∠AMF=90°, 在Rt△AFN和Rt△AFM中
????=????
????=????
, ∴Rt△AFN≌Rt△AFM(HL), ∴NF=MF, ∴BF+CF=BN+NF+CM﹣MF, =BN+CM=2BN=n, ∴BN=
??
2
, ∴在Rt△ABN中,AB2=BN2+AN2=m2+
??
2
2
=m2+
??
2
4
, 在Rt△ACD中,CD2=AB2+AC2=2AB2=2m2+
??
2
2
, ∴CD=
1
2
8
??
2
+2
??
2
.??????????????????????????????????? (3)解:
????
????
的值不发生变化, 过点D作DH⊥AO于H,过点D作DQ⊥BC于Q,??????????? ∵∠DAH+∠OAC=90°,∠DAH+∠ADH=90°, ∴∠OAC=∠ADH, 在△DHA和△AOC中
∠??????=∠??????
∠??????=∠??????
????=????
, ∴Rt△DHA≌Rt△AOC(AAS), ∴DH=AO,AH=OC, 又∵BO=OC, ∴HO=AH+AO=OB+DH, 而DH=OQ,HO=DQ, ∴DQ=OB+OQ=BQ, ∴∠DBQ=45°, 又∵DH∥BC, ∴∠HDE=45°, ∴△DHE为等腰直角三角形, ∴
????
????
=
2
, ∴
????
????
=
2
. //?
一、单选题(共10题;共30分)
1.已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是(?? )
A.?点P在⊙O内??????????????????????/B.?点P在⊙O上??????????????????????/C.?点P在⊙O外??????????????????????/D.?无法判断
2.如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是(?? ) /
A.?42°???????????????????????????????????????B.?21°???????????????????????????????????????C.?84°???????????????????????????????????????D.?60°
3.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为(?? ) /
A.?3?????????????????????????????????????????/B.?2.5?????????????????????????????????????????/C.?4?????????????????????????????????????????/D.?3.5
4.已知AB=7cm,则过点A,B,且半径为3cm的圆有( )
A.?0个????????????????????????????????????/B.?1个????????????????????????????????????/C.?2个??????????????????????????????????????/D.?无数个
5.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,CM切⊙O于点C,∠BCM=60°,则∠B的正切值是( )
A.?
1
2
???????????????????????????????????????/B.?
3
3
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
3
6.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是(??) /
A.?25°???????????????????????????????????????B.?30°???????????????????????????????????????C.?35°???????????????????????????????????????D.?40°
7.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( ) ?/
A.?2π????????????????????????????????????B.?4π????????????????????????????????????C.?5π??? ????????????????????????????????????D.?6π
8.如图,⊙O是△ABC的外接圆,已知∠ABO=30o,则∠ACB的大小为?????????( ??) /
A.?60o??????????????????????????????????????/B.?30o??????????????????????????????????????/C.?45o??????????????????????????????????????/D.?50o
9.如图,将△ABC绕点C顺时针方向旋转40°,得△A′CB′,若AC⊥A′B′,则∠BAC等于(?? ) /
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
10.如图,点C是⊙O上一点,⊙O的半径为 2
2
,D、E分别是弦AC、BC上一动点,且OD=OE=
2
,则AB的最大值为(?? ) /
A.?2
6
?????????????????????????????????????/B.?2
3
?????????????????????????????????????/C.?2
2
?????????????????????????????????????/D.?4
2
二、填空题(共10题;共30分)
11.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的直径________cm.
12.如图所示,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积是________./
13.如图:在△ABC中,∠A、∠B的对边分别为a、b,且∠C=90°,分别以AC、BC为直径作半圆,则图中阴影部分的面积为________?
/
14.在矩形ABCD中,AB=4,BC=6,动点P为矩形边上的一点,点P沿着B﹣C的路径运动(含点B和点C),则△ADP的外接圆的圆心O的运动路径长是________. //
15.如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为________.
16.如图,AB是⊙O的直径,AB=15,AC=9,则cos∠ADC=________. /
17.如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为________. /
18.下列说法:①弦是直径;②直径是弦;③过圆心的线段是直径;④一个圆的直径只有一条.其中正确的是 ________?(填序号).
19.如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是________. /
20.(2017?泰州)如图,在平面直角坐标系xOy中,点A,B,P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为________. /
三、解答题(共9题;共60分)
21.(2017?宁波)在 4×4 的方格中,△ABC的三个顶点都在格点上. /
(1)在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);
(2)将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.
22.如图,
????
是⊙D的
1
4
圆周,点C在
????
上运动,求∠BCD的取值范围.
/
23.如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少? /
24.如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证: / (1)D是BC的中点; (2)△BEC∽△ADC.
25.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在
????
∧
上. (1)求∠AED的度数; (2)若⊙O的半径为2,则
????
∧
的长为多少? (3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值. /
26.如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G. / (1)求证:△BDG∽△DEG; (2)若EG·BG=4,求BE的长.
27.△ABC和△ECD都是等边三角形 / (1)如图1,若B、C、D三点在一条直线上,求证:BE=AD; (2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
28.如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF. / (1)求证:△ADE≌△ABF; (2)填空:△ABF可以由△ADE绕旋转中心 ?????点,按顺时针方向旋转 ???度得到; (3)若BC=8,DE=6,求△AEF的面积.
29.如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC. (1)求证:∠ACF=∠ADB; (2)若点A到BD的距离为m,BF+CF=n,求线段CD的长; (3)当⊙P的大小发生变化而其他条件不变时,
????
????
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由. /
答案解析部分
一、单选题
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】A
9.【答案】A
10.【答案】A
二、填空题
11.【答案】10
12.【答案】4-
8
9
π
13.【答案】
1
8
π
a
2
+
b
2
?
1
2
ab
14.【答案】
9
4
15.【答案】
3
16.【答案】
4
5
17.【答案】(3,3)
18.【答案】②
19.【答案】22°
20.【答案】(7,4)或(6,5)或(1,4)
三、解答题
21.【答案】(1)解:画出下列其中一个即可. / (2)解: /
22.【答案】解:∵
????
是⊙D的
1
4
圆周,
∴∠BDE=
1
4
×360°=90°,
∵DB=DC,
∴∠B=∠BCD,
∴∠BCD=
1
2
(180°﹣∠BDC)=90°﹣
1
2
∠BDC,
而0≤∠BDC≤90°,
∴45°≤∠BCD≤90°
23.【答案】解:如图, / 过点A作AC⊥ON, ∵∠MON=30°,OA=80米, ∴AC=40米, 当第一台拖拉机到B点时对学校产生噪音影响,此时AB=50, 由勾股定理得:BC=30, 第一台拖拉机到D点时噪音消失, 所以CD=30. 由于两台拖拉机相距30米,则第一台到D点时第二台在C点,还须前行30米后才对学校没有噪音影响. 所以影响时间应是:90÷5=18秒. 答:这两台拖拉机沿ON方向行驶给小学带来噪音影响的时间是18秒
24.【答案】解:(1)证明: ∵AB为⊙O的直径, ∴∠BDA=90°, ∴AD⊥BC. ∵AB=AC. ∴BD=CD, ∴D是BC的中点; (2)∵AB=AC, ∴∠C=∠ABD, ∵AB为⊙O的直径, ∴∠ADB=∠BEC=90°, ∴△BEC∽△ADC;
25.【答案】解:(1)连接BD,如图1所示: ∵四边形ABCD是⊙O的内接四边形, ∴∠BAD+∠C=180°, ∵∠C=120°, ∴∠BAD=60°, ∵AB=AD, ∴△ABD是等边三角形, ∴∠ABD=60°, ∵四边形ABDE是⊙O的内接四边形,∴∠AED+∠ABD=180°, ∴∠AED=120°; (2)∵∠AOD=2∠ABD=120°, ∴
????
∧
的长=
120×π×2
180
=
4π
3
; (3)连接OA,如图2所示: ∵∠ABD=60°, ∴∠AOD=2∠ABD=120°, ∵∠DOE=90°, ∴∠AOE=∠AOD﹣∠DOE=30°, ∴n=
360°
30°
=12. /
26.【答案】(1)证明:∵将△BCE绕点C顺时针旋转到△DCF的位置,∴△BCE≌△DCF, ∴∠FDC=∠EBC,∵BE平分∠DBC, ∴∠DBE=∠EBC,∴∠FDC=∠EBD, ∵∠DGE=∠DGE,∴△BDG∽△DEG. (2)解:∵△BCE≌△DCF, ∴∠F=∠BEC,∠EBC=∠FDC, ∵四边形ABCD是正方形, ∴∠DCB=90°,∠DBC=∠BDC=45°, ∵BE平分∠DBC, ∴∠DBE=∠EBC=22.5°=∠FDC, ∴∠BDF=45°+22.5°=67.5°, ∠F=90°-22.5°=67.5°=∠BDF, ∴BD=BF,∵△BCE≌△DCF, ∴∠F=∠BEC=67.5°=∠DEG, ∴∠DGB=180°-22.5°-67.5°=90°, 即BG⊥DF,∵BD=BF,∴DF=2DG, ∵△BDG∽△DEG,BG·EG=4, ∴
????
????
=
????
????
, ∴BG·EG=DG·DG=4, ∴DG=2,∴BE=DF=2DG=4.
27.【答案】解:(1)∵△ABC和△ECD都是等边三角形,∴AC=BC,EC=DC,∠ACB=∠ECD=60°. ∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE. ∴△ACD≌△BCE. ∴AD=BE. (2)BC垂直平分DE,理由如下: 如图, / 延长BC交DE于M, ∵∠ACB=60°,∠ACE=90°,∴∠ECM=180°-∠ACB-∠ACE=30°. ∵∠DCM=∠ECD-∠ECM=30°,∴∠ECM=∠DCM. ∵△ECD是等边三角形,∴CM垂直平分DE,即BC垂直平分DE.
28.【答案】解;(1)∵四边形ABCD是正方形, ∴AD=AB,∠D=∠ABC=90°, ∴∠ABF=90°, 在△ADE和△ABF中,
????=????
∠??????=∠??????
????=????
, ∴△ADE≌△ABF(SAS) (2)A、90; (3)∵在正方形ABCD中,AD=BC=8,DE=6,∠D=90°, ∴AE=
??
??
2
+??
??
2
=10, ∵△ABF可以由△ADE绕A点顺时针方向旋转90°得到, ∴AE=AF,∠EAF=90°, ∴△AEF的面积=
1
2
AE2=
1
2
×100=50(平方单位).
29.【答案】(1)证明:连接AB, ∵OP⊥BC, ∴BO=CO, ∴AB=AC, 又∵AC=AD, ∴AB=AD, ∴∠ABD=∠ADB, 又∵∠ABD=∠ACF, ∴∠ACF=∠ADB.???? (2)解:过点A作AM⊥CF交CF的延长线于M,过点A作AN⊥BF于N,连接AF, 则AN=m, ∴∠ANB=∠AMC=90°, 在△ABN和△ACM中 ,
∠??????=∠??????
∠??????=∠??????
????=????
∴Rt△ABN≌Rt△ACM(AAS) ∴BN=CM,AN=AM, 又∵∠ANF=∠AMF=90°, 在Rt△AFN和Rt△AFM中
????=????
????=????
, ∴Rt△AFN≌Rt△AFM(HL), ∴NF=MF, ∴BF+CF=BN+NF+CM﹣MF, =BN+CM=2BN=n, ∴BN=
??
2
, ∴在Rt△ABN中,AB2=BN2+AN2=m2+
??
2
2
=m2+
??
2
4
, 在Rt△ACD中,CD2=AB2+AC2=2AB2=2m2+
??
2
2
, ∴CD=
1
2
8
??
2
+2
??
2
.??????????????????????????????????? (3)解:
????
????
的值不发生变化, 过点D作DH⊥AO于H,过点D作DQ⊥BC于Q,??????????? ∵∠DAH+∠OAC=90°,∠DAH+∠ADH=90°, ∴∠OAC=∠ADH, 在△DHA和△AOC中
∠??????=∠??????
∠??????=∠??????
????=????
, ∴Rt△DHA≌Rt△AOC(AAS), ∴DH=AO,AH=OC, 又∵BO=OC, ∴HO=AH+AO=OB+DH, 而DH=OQ,HO=DQ, ∴DQ=OB+OQ=BQ, ∴∠DBQ=45°, 又∵DH∥BC, ∴∠HDE=45°, ∴△DHE为等腰直角三角形, ∴
????
????
=
2
, ∴
????
????
=
2
. //?
同课章节目录
