【期末专题复习】浙教版九年级数学下册《第二章直线和圆的位置关系》单元检测试卷(含答案)
文档属性
| 名称 | 【期末专题复习】浙教版九年级数学下册《第二章直线和圆的位置关系》单元检测试卷(含答案) | 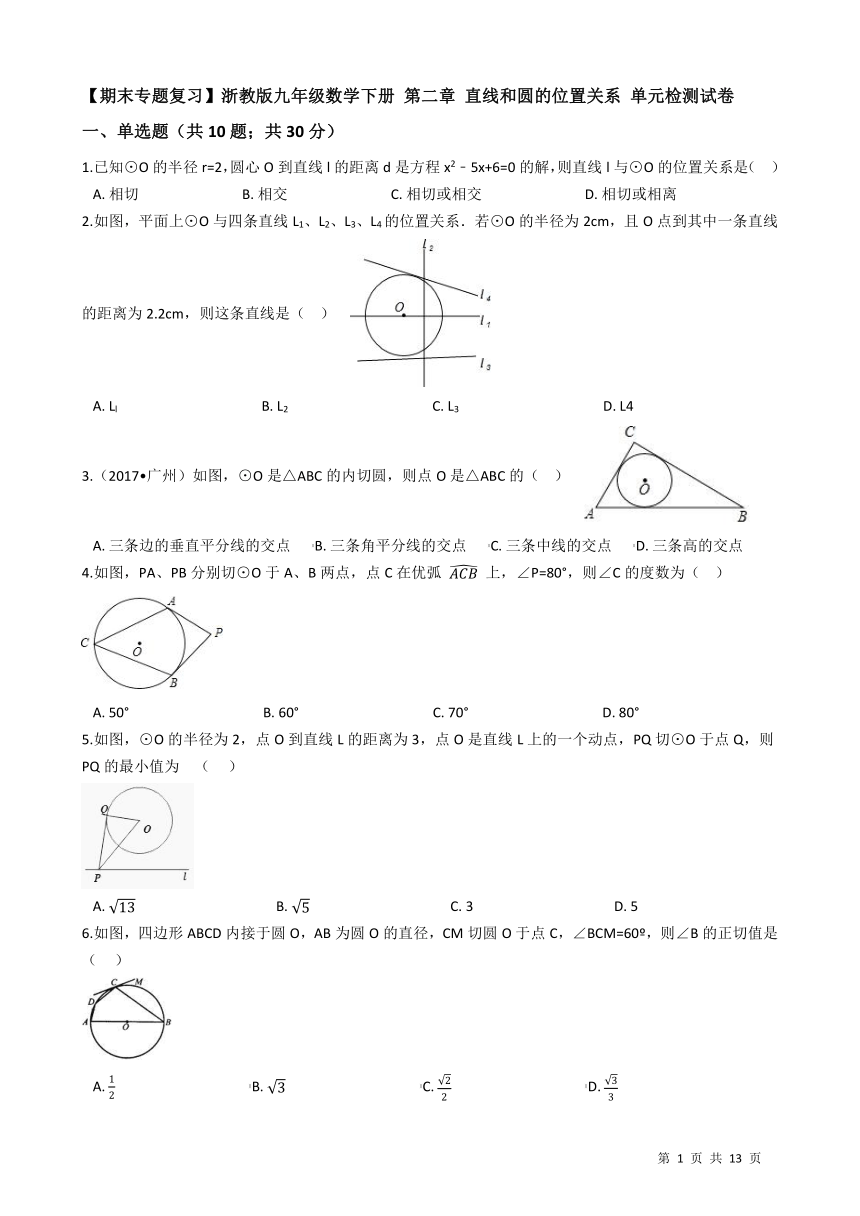 | |
| 格式 | zip | ||
| 文件大小 | 235.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-24 19:16:06 | ||
图片预览



文档简介
【期末专题复习】浙教版九年级数学下册 第二章 直线和圆的位置关系 单元检测试卷
一、单选题(共10题;共30分)
1.已知⊙O的半径r=2,圆心O到直线l的距离d是方程x2﹣5x+6=0的解,则直线l与⊙O的位置关系是(?? )
A.?相切??????????????????????????????B.?相交??????????????????????????????C.?相切或相交??????????????????????????????D.?相切或相离
2.如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是(?? ) /
A.?Ll??????????????????????????????????????????B.?L2??????????????????????????????????????????C.?L3??????????????????????????????????????????D.?L4
3.(2017?广州)如图,⊙O是△ABC的内切圆,则点O是△ABC的(?? ) /
A.?三条边的垂直平分线的交点??????/B.?三条角平分线的交点??????/C.?三条中线的交点??????/D.?三条高的交点
4.如图,PA、PB分别切⊙O于A、B两点,点C在优弧
??????
上,∠P=80°,则∠C的度数为(?? ) /
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
5.如图,⊙O的半径为2,点O到直线L的距离为3,点O是直线L上的一个动点,PQ切⊙O于点Q,则PQ的最小值为 ( ???) /
A.?
13
?????????????????????????????????????????B.?
5
?????????????????????????????????????????C.?3?????????????????????????????????????????D.?5
6.如图,四边形ABCD内接于圆O,AB为圆O的直径,CM切圆O于点C,∠BCM=60o,则∠B的正切值是(?????) /
A.?
1
2
???????????????????????????????????????/B.?
3
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
3
3
7.在平面直角坐标系中,抛物线y=-(x-2)2+1的顶点是点P,对称轴与x轴相交于点Q,以点P为圆心,PQ长为半径画⊙P,那么下列判断正确的是(????)
A.?x轴与⊙P相离;????????????B.?x轴与⊙P相切;????????????C.?y轴与⊙P与相切;????????????D.?y轴与⊙P相交.
8.下列说法正确的是()
A.?垂直于半径的直线是圆的切线?????????????????????????????/B.?经过三个点一定可以作圆 C.?圆的切线垂直于圆的半径????????????????????????????????????/D.?每个三角形都有一个内切圆
9.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为(??????? ) /
A.?40°???????????????????????????????????????B.?50°???????????????????????????????????????C.?60°???????????????????????????????????????D.?80°
10.在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( ) /
A.?AF=4,BD=9,CE=5????????????????????????????????????????/B.?AF=4,BD=5,CE=9 C.?AF=5,BD=4,CE=9????????????????????????????????????????/D.?AF=9,BD=4,CE=5
二、填空题(共10题;共33分)
11.如图,四边形ABCD是平行四边形,其中边AD是⊙O的直径,BC与⊙O相切于点B,若⊙O的周长是12π,则四边形ABCD的面积为________. /
12.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=
1
2
,则AB的长是________. /
13.三角形的内切圆的切点将该圆周分为5:9:10三条弧,则此三角形的最小的内角为________.
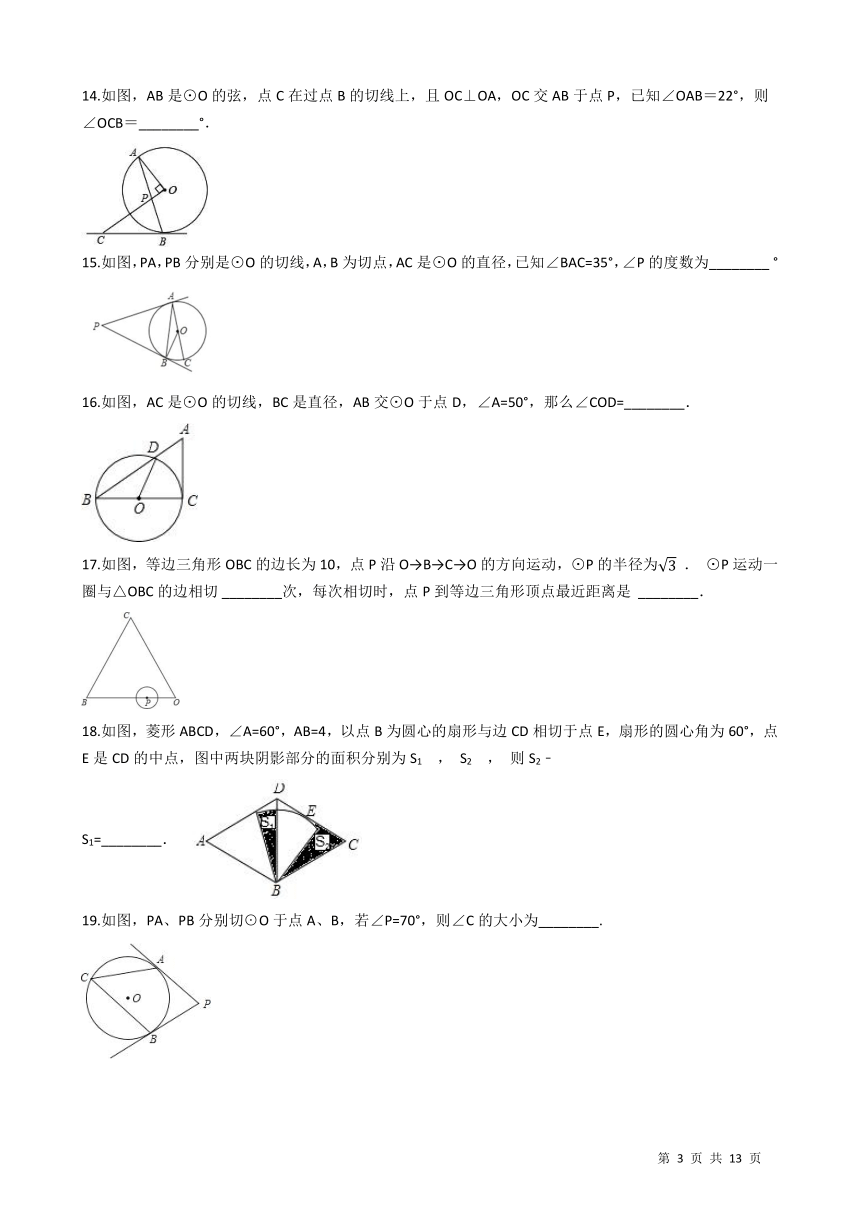
14.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=________°. /
15.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为________?° /
16.如图,AC是⊙O的切线,BC是直径,AB交⊙O于点D,∠A=50°,那么∠COD=________.
17.如图,等边三角形OBC的边长为10,点P沿O→B→C→O的方向运动,⊙P的半径为
3
. ⊙P运动一圈与△OBC的边相切?________次,每次相切时,点P到等边三角形顶点最近距离是??________. /
18.如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1=________. /
19.如图,PA、PB分别切?O于点A、B,若∠P=70°,则∠C的大小为________. /
20.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________。/
三、解答题(共9题;共57分)
21.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线. /
22.如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
1
2
ED,延长DB到点F,使DB到点F,使FB=
1
2
BD,连接AF. / ⑴△BDE∽△FDA; ⑵试判断直线AF与⊙O的位置关系,并给出证明。
23.如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF. / (1)求证:直线PA为⊙O的切线; (2)试探究线段EF,OD,OP之间的等量关系,并加以证明; (3)若BC=6,tan∠F=
1
2
,求cos∠ACB的值和线段PE的长.
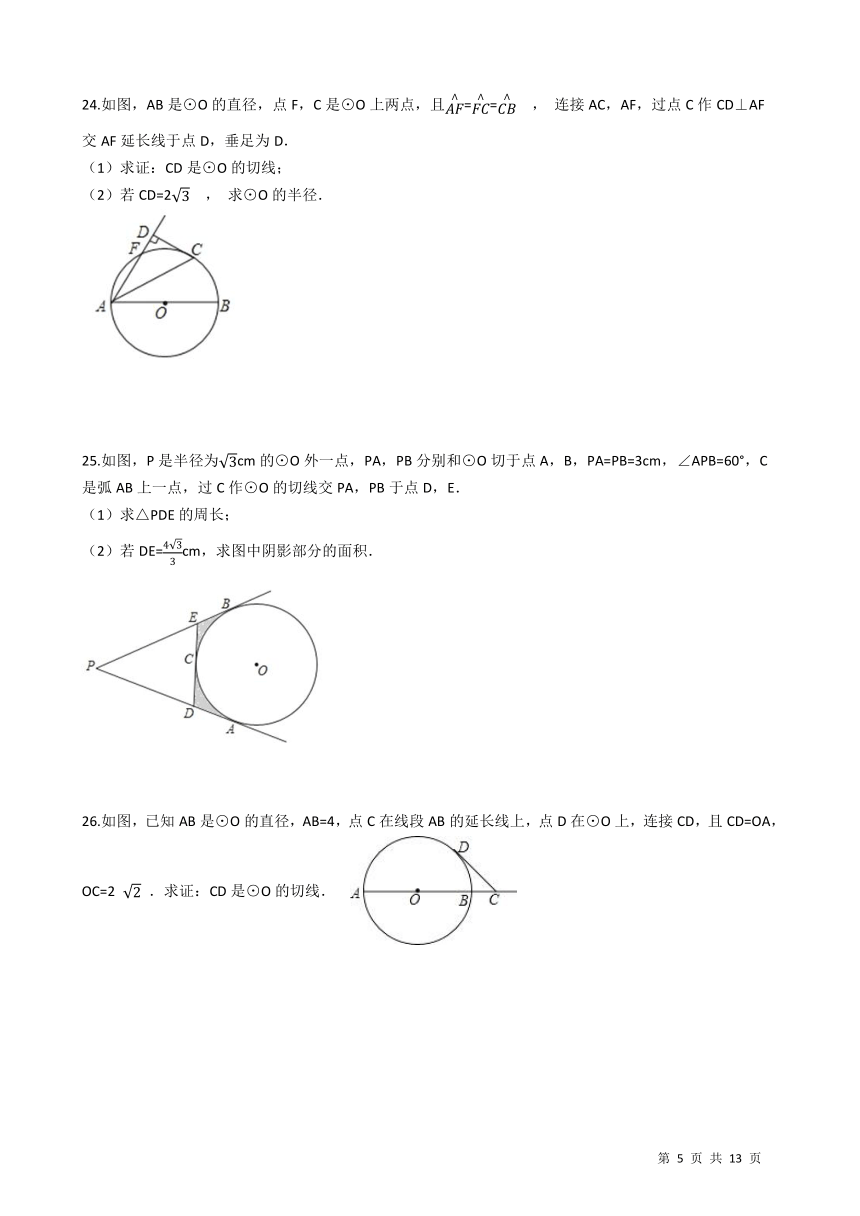
24.如图,AB是⊙O的直径,点F,C是⊙O上两点,且
????
∧
=
????
∧
=
????
∧
, 连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D. (1)求证:CD是⊙O的切线; (2)若CD=2
3
, 求⊙O的半径. ?/
25.如图,P是半径为
3
cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E. (1)求△PDE的周长; (2)若DE=
4
3
3
cm,求图中阴影部分的面积. /
26.如图,已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上,点D在⊙O上,连接CD,且CD=OA,OC=2
2
.求证:CD是⊙O的切线. /
27.在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G. (1)求证:内切圆的半径r=1; (2)求tan∠OAG的值. /
28.已知△ABC内接于⊙O , AC是⊙O的直径,D是弧AB的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E . /
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
29.如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连接BC. (Ⅰ)如图①,若∠P=20°,求∠BCO的度数; (Ⅱ)如图②,过A作弦AD⊥OP于E,连接DC,若OE=
1
2
CD,求∠P的度数. /
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】A
二、填空题
11.【答案】72
12.【答案】8
13.【答案】30°
14.【答案】44
15.【答案】70
16.【答案】80°
17.【答案】6;2
18.【答案】2
3
﹣π
19.【答案】55°
20.【答案】3或 4
3
三、解答题
21.【答案】证明:连接OD; ∵AD平行于OC, ∴∠COD=∠ODA,∠COB=∠A; ∵∠ODA=∠A, ∴∠COD=∠COB,OC=OC,OD=OB, ∴△OCD≌△OCB, ∴∠CDO=∠CBO=90°. ∴DC是⊙O的切线.
22.【答案】解:(1)在△BDE和△FDA中, ∵FB=
1
2
BD,AE=
1
2
ED,AD=AE+ED,FD=FB+BD ∴
????
????
=
????
????
=
2
3
, 又∵∠BDE=∠FDA, ∴△BDE∽△FDA. (2)直线AF与⊙O相切. 证明:连接OA,OB,OC, ∵AB=AC,BO=CO,OA=OA, ∴△OAB≌△OAC, ∴∠OAB=∠OAC, ∴AO是等腰三角形ABC顶角∠BAC的平分线, ∴AB=AC, ∴AO⊥BC, ∵△BDE∽△FDA,得∠EBD=∠AFD, ∴BE∥FA, ∵AO⊥BE知,AO⊥FA, ∴直线AF与⊙O相切.
23.【答案】(1)证明:如图,连接OB, ∵PB是⊙O的切线,∴∠PBO=90°. ∵OA=OB,BA⊥PO于D,∴AD=BD,∠POA=∠POB. 又∵PO=PO,∴△PAO≌△PBO(SAS). ∴∠PAO="∠PBO=90°." ∴直线PA为⊙O的切线. / (2)解:EF2=4OD?OP,证明如下: ∵∠PAO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°. ∴∠OAD=∠OPA. ∴△OAD∽△OPA. ∴
????
????
=
????
????
,即OA2=OD?OP. 又∵EF=2OA,∴EF2=4OD?OP. (3)解:∵OA=OC,AD=BD,BC=6,∴OD=
1
2
BC=3(三角形中位线定理). 设AD=x, ∵tan∠F=
????
????
=
1
2
,∴FD=2x,OA=OF=2x﹣3. 在Rt△AOD中,由勾股定理,得(2x﹣3)2=x2+32 , 解得,x1=4,x2=0(不合题意,舍去).∴AD=4,OA=2x﹣3=5. ∵AC是⊙O直径,∴∠ABC=90°. 又∵AC=2OA=10,BC=6,∴cos∠ACB=
????
????
=
6
10
=
3
5
. ∵OA2=OD?OP,∴3(PE+5)=25.∴PE=
10
3
.
24.【答案】(1)证明:连结OC,如图, ∵
????
∧
=
????
∧
, ∴∠FAC=∠BAC, ∵OA=OC, ∴∠OAC=∠OCA, ∴∠FAC=∠OCA, ∴OC∥AF, ∵CD⊥AF, ∴OC⊥CD, ∴CD是⊙O的切线; (2)解:连结BC,如图, ∵AB为直径, ∴∠ACB=90°, ∵
????
∧
=
????
∧
=
????
∧
, ∴∠BOC=
1
3
×180°=60°, ∴∠BAC=30°, ∴∠DAC=30°, 在Rt△ADC中,CD=2
3
, ∴AC=2CD=4
3
, 在Rt△ACB中,BC=
3
3
AC=
3
3
×4
3
=4, ∴AB=2BC=8, ∴⊙O的半径为4. ?/
25.【答案】解:(1)∵PA、PB、DE是⊙O的切线, ∴PA=PB=3cm,CE=BE,AD=DC, ∴△PDE的周长=PE+DE+PD=PE+CE+CD+PD =PE+BE+AD+PD =PA+PB =3cm+3cm =6cm; (2)连接OB、OA、OE,OD,如图, ∵PA、PB、OC是⊙O的切线, ∴OB⊥PB,OA⊥PA,OC⊥DE, ∴∠OBP=∠OPA=90°, ∵∠APB=60°, ∴∠BOA=120°, ∵BE=CE,DC=DA, ∴S△OCE=S△OBE , S△OCD=S△ODA , ∴S五边AOBED=2S△ODE=2×
1
2
×
4
3
3
×
3
=4, ∴图中阴影部分的面积=S五边AOBED﹣S扇形AOB=4﹣
120·π·
3
2
360
=(4﹣π)cm2 . /
26.【答案】证明:连接OD,如图, CD=OD=OA= /AB=2,OC=2 /, ∵22+22=(2 /)2 , ∴OD2+CD2=OC2 , ∴△OCD为直角三角形,∠ODC=90°, ∴OD⊥CD, 又∵点D在⊙O上, ∴CD是⊙O的切线. /
27.【答案】(1)证明:如图连结OE,OF,OG. ∵⊙O是△ABC的内切圆,∠C=90°, ∴四边形CEOF是正方形, ∴CE=CF=r. 又∵AG=AE=3﹣r,BG=BF=4﹣r,AG+BG=5, ∴(3﹣r)+(4﹣r)=5. 解得r=1; (2)解:连结OA,在Rt△AOG中, ∵r=1,AG=3﹣r=2, tan∠OAG=
????
????
=
1
2
. /
28.【答案】(1)解:直线EF与⊙O相切,理由为: 连接OD,如图所示: ∵AC为⊙O的直径, ∴∠CBA=90° 又∵∠F=90° ∴∠CBA=∠F ∴AB‖EF ∴∠AMO=∠EDO 又∵D为弧AB的中点 ∴弧BD=弧AD ∴OD⊥AB ∴∠AMO=∠EDO=90° ∴EF为⊙O的切线 / (2)shan 解:在Rt△AEF中,∠ACB=60° ∴∠E=30° 又∵CF=6 ∴CE=2CF=12 ∴EF=
??
??
2
???
??
2
=6
3
在Rt△ODE中,∠E=30° ∴OD=
1
2
OE 又∵OA=
1
2
OE ∴OA=AE=OC=
1
3
CE=4,OE=8 又∵∠ODE=∠F=90°,∠E=∠E ∴△ODE∽△CFE ∴
????
????
=
????
????
,即
4
6
=
????
6
3
∴DE=4
3
又∵Rt△ODE中,∠E=30° ∴∠DOE=60° ∴ S阴影=
??
△??????
?S扇形OAD=
1
2
×4×4
3
-
60·π·
4
2
360
=8
3
-
8π
3
29.【答案】解:(Ⅰ)如图1中, / ∵PA是⊙O的切线, ∴OA⊥AP, ∴∠PAO=90°,∵∠P=20°, ∴∠AOC=90°﹣20°=70°, ∴∠B=
1
2
∠AOC=35°, ∵OB=OC, ∴∠B=∠OCB=35°, ∴∠BCO=35°. (Ⅱ)如图2中,连接BD、OD. / ∵AD⊥OP于E, ∴AE=ED,
????
=
????
, ∵AE=ED,OA=OB, ∴OE=
1
2
DB, ∵OE=
1
2
CD, ∴CD=DB, ∴
????
=
????
, ∴
????
=
????
=
????
, ∴∠AOC=∠COD=∠BOD=60°, ∵PA是⊙O的切线, ∴∠PAO=90°, ∴∠P=30°
一、单选题(共10题;共30分)
1.已知⊙O的半径r=2,圆心O到直线l的距离d是方程x2﹣5x+6=0的解,则直线l与⊙O的位置关系是(?? )
A.?相切??????????????????????????????B.?相交??????????????????????????????C.?相切或相交??????????????????????????????D.?相切或相离
2.如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是(?? ) /
A.?Ll??????????????????????????????????????????B.?L2??????????????????????????????????????????C.?L3??????????????????????????????????????????D.?L4
3.(2017?广州)如图,⊙O是△ABC的内切圆,则点O是△ABC的(?? ) /
A.?三条边的垂直平分线的交点??????/B.?三条角平分线的交点??????/C.?三条中线的交点??????/D.?三条高的交点
4.如图,PA、PB分别切⊙O于A、B两点,点C在优弧
??????
上,∠P=80°,则∠C的度数为(?? ) /
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
5.如图,⊙O的半径为2,点O到直线L的距离为3,点O是直线L上的一个动点,PQ切⊙O于点Q,则PQ的最小值为 ( ???) /
A.?
13
?????????????????????????????????????????B.?
5
?????????????????????????????????????????C.?3?????????????????????????????????????????D.?5
6.如图,四边形ABCD内接于圆O,AB为圆O的直径,CM切圆O于点C,∠BCM=60o,则∠B的正切值是(?????) /
A.?
1
2
???????????????????????????????????????/B.?
3
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
3
3
7.在平面直角坐标系中,抛物线y=-(x-2)2+1的顶点是点P,对称轴与x轴相交于点Q,以点P为圆心,PQ长为半径画⊙P,那么下列判断正确的是(????)
A.?x轴与⊙P相离;????????????B.?x轴与⊙P相切;????????????C.?y轴与⊙P与相切;????????????D.?y轴与⊙P相交.
8.下列说法正确的是()
A.?垂直于半径的直线是圆的切线?????????????????????????????/B.?经过三个点一定可以作圆 C.?圆的切线垂直于圆的半径????????????????????????????????????/D.?每个三角形都有一个内切圆
9.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为(??????? ) /
A.?40°???????????????????????????????????????B.?50°???????????????????????????????????????C.?60°???????????????????????????????????????D.?80°
10.在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( ) /
A.?AF=4,BD=9,CE=5????????????????????????????????????????/B.?AF=4,BD=5,CE=9 C.?AF=5,BD=4,CE=9????????????????????????????????????????/D.?AF=9,BD=4,CE=5
二、填空题(共10题;共33分)
11.如图,四边形ABCD是平行四边形,其中边AD是⊙O的直径,BC与⊙O相切于点B,若⊙O的周长是12π,则四边形ABCD的面积为________. /
12.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=
1
2
,则AB的长是________. /
13.三角形的内切圆的切点将该圆周分为5:9:10三条弧,则此三角形的最小的内角为________.
14.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=________°. /
15.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为________?° /
16.如图,AC是⊙O的切线,BC是直径,AB交⊙O于点D,∠A=50°,那么∠COD=________.
17.如图,等边三角形OBC的边长为10,点P沿O→B→C→O的方向运动,⊙P的半径为
3
. ⊙P运动一圈与△OBC的边相切?________次,每次相切时,点P到等边三角形顶点最近距离是??________. /
18.如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1=________. /
19.如图,PA、PB分别切?O于点A、B,若∠P=70°,则∠C的大小为________. /
20.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________。/
三、解答题(共9题;共57分)
21.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线. /
22.如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
1
2
ED,延长DB到点F,使DB到点F,使FB=
1
2
BD,连接AF. / ⑴△BDE∽△FDA; ⑵试判断直线AF与⊙O的位置关系,并给出证明。
23.如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF. / (1)求证:直线PA为⊙O的切线; (2)试探究线段EF,OD,OP之间的等量关系,并加以证明; (3)若BC=6,tan∠F=
1
2
,求cos∠ACB的值和线段PE的长.
24.如图,AB是⊙O的直径,点F,C是⊙O上两点,且
????
∧
=
????
∧
=
????
∧
, 连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D. (1)求证:CD是⊙O的切线; (2)若CD=2
3
, 求⊙O的半径. ?/
25.如图,P是半径为
3
cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E. (1)求△PDE的周长; (2)若DE=
4
3
3
cm,求图中阴影部分的面积. /
26.如图,已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上,点D在⊙O上,连接CD,且CD=OA,OC=2
2
.求证:CD是⊙O的切线. /
27.在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G. (1)求证:内切圆的半径r=1; (2)求tan∠OAG的值. /
28.已知△ABC内接于⊙O , AC是⊙O的直径,D是弧AB的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E . /
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
29.如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连接BC. (Ⅰ)如图①,若∠P=20°,求∠BCO的度数; (Ⅱ)如图②,过A作弦AD⊥OP于E,连接DC,若OE=
1
2
CD,求∠P的度数. /
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】A
二、填空题
11.【答案】72
12.【答案】8
13.【答案】30°
14.【答案】44
15.【答案】70
16.【答案】80°
17.【答案】6;2
18.【答案】2
3
﹣π
19.【答案】55°
20.【答案】3或 4
3
三、解答题
21.【答案】证明:连接OD; ∵AD平行于OC, ∴∠COD=∠ODA,∠COB=∠A; ∵∠ODA=∠A, ∴∠COD=∠COB,OC=OC,OD=OB, ∴△OCD≌△OCB, ∴∠CDO=∠CBO=90°. ∴DC是⊙O的切线.
22.【答案】解:(1)在△BDE和△FDA中, ∵FB=
1
2
BD,AE=
1
2
ED,AD=AE+ED,FD=FB+BD ∴
????
????
=
????
????
=
2
3
, 又∵∠BDE=∠FDA, ∴△BDE∽△FDA. (2)直线AF与⊙O相切. 证明:连接OA,OB,OC, ∵AB=AC,BO=CO,OA=OA, ∴△OAB≌△OAC, ∴∠OAB=∠OAC, ∴AO是等腰三角形ABC顶角∠BAC的平分线, ∴AB=AC, ∴AO⊥BC, ∵△BDE∽△FDA,得∠EBD=∠AFD, ∴BE∥FA, ∵AO⊥BE知,AO⊥FA, ∴直线AF与⊙O相切.
23.【答案】(1)证明:如图,连接OB, ∵PB是⊙O的切线,∴∠PBO=90°. ∵OA=OB,BA⊥PO于D,∴AD=BD,∠POA=∠POB. 又∵PO=PO,∴△PAO≌△PBO(SAS). ∴∠PAO="∠PBO=90°." ∴直线PA为⊙O的切线. / (2)解:EF2=4OD?OP,证明如下: ∵∠PAO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°. ∴∠OAD=∠OPA. ∴△OAD∽△OPA. ∴
????
????
=
????
????
,即OA2=OD?OP. 又∵EF=2OA,∴EF2=4OD?OP. (3)解:∵OA=OC,AD=BD,BC=6,∴OD=
1
2
BC=3(三角形中位线定理). 设AD=x, ∵tan∠F=
????
????
=
1
2
,∴FD=2x,OA=OF=2x﹣3. 在Rt△AOD中,由勾股定理,得(2x﹣3)2=x2+32 , 解得,x1=4,x2=0(不合题意,舍去).∴AD=4,OA=2x﹣3=5. ∵AC是⊙O直径,∴∠ABC=90°. 又∵AC=2OA=10,BC=6,∴cos∠ACB=
????
????
=
6
10
=
3
5
. ∵OA2=OD?OP,∴3(PE+5)=25.∴PE=
10
3
.
24.【答案】(1)证明:连结OC,如图, ∵
????
∧
=
????
∧
, ∴∠FAC=∠BAC, ∵OA=OC, ∴∠OAC=∠OCA, ∴∠FAC=∠OCA, ∴OC∥AF, ∵CD⊥AF, ∴OC⊥CD, ∴CD是⊙O的切线; (2)解:连结BC,如图, ∵AB为直径, ∴∠ACB=90°, ∵
????
∧
=
????
∧
=
????
∧
, ∴∠BOC=
1
3
×180°=60°, ∴∠BAC=30°, ∴∠DAC=30°, 在Rt△ADC中,CD=2
3
, ∴AC=2CD=4
3
, 在Rt△ACB中,BC=
3
3
AC=
3
3
×4
3
=4, ∴AB=2BC=8, ∴⊙O的半径为4. ?/
25.【答案】解:(1)∵PA、PB、DE是⊙O的切线, ∴PA=PB=3cm,CE=BE,AD=DC, ∴△PDE的周长=PE+DE+PD=PE+CE+CD+PD =PE+BE+AD+PD =PA+PB =3cm+3cm =6cm; (2)连接OB、OA、OE,OD,如图, ∵PA、PB、OC是⊙O的切线, ∴OB⊥PB,OA⊥PA,OC⊥DE, ∴∠OBP=∠OPA=90°, ∵∠APB=60°, ∴∠BOA=120°, ∵BE=CE,DC=DA, ∴S△OCE=S△OBE , S△OCD=S△ODA , ∴S五边AOBED=2S△ODE=2×
1
2
×
4
3
3
×
3
=4, ∴图中阴影部分的面积=S五边AOBED﹣S扇形AOB=4﹣
120·π·
3
2
360
=(4﹣π)cm2 . /
26.【答案】证明:连接OD,如图, CD=OD=OA= /AB=2,OC=2 /, ∵22+22=(2 /)2 , ∴OD2+CD2=OC2 , ∴△OCD为直角三角形,∠ODC=90°, ∴OD⊥CD, 又∵点D在⊙O上, ∴CD是⊙O的切线. /
27.【答案】(1)证明:如图连结OE,OF,OG. ∵⊙O是△ABC的内切圆,∠C=90°, ∴四边形CEOF是正方形, ∴CE=CF=r. 又∵AG=AE=3﹣r,BG=BF=4﹣r,AG+BG=5, ∴(3﹣r)+(4﹣r)=5. 解得r=1; (2)解:连结OA,在Rt△AOG中, ∵r=1,AG=3﹣r=2, tan∠OAG=
????
????
=
1
2
. /
28.【答案】(1)解:直线EF与⊙O相切,理由为: 连接OD,如图所示: ∵AC为⊙O的直径, ∴∠CBA=90° 又∵∠F=90° ∴∠CBA=∠F ∴AB‖EF ∴∠AMO=∠EDO 又∵D为弧AB的中点 ∴弧BD=弧AD ∴OD⊥AB ∴∠AMO=∠EDO=90° ∴EF为⊙O的切线 / (2)shan 解:在Rt△AEF中,∠ACB=60° ∴∠E=30° 又∵CF=6 ∴CE=2CF=12 ∴EF=
??
??
2
???
??
2
=6
3
在Rt△ODE中,∠E=30° ∴OD=
1
2
OE 又∵OA=
1
2
OE ∴OA=AE=OC=
1
3
CE=4,OE=8 又∵∠ODE=∠F=90°,∠E=∠E ∴△ODE∽△CFE ∴
????
????
=
????
????
,即
4
6
=
????
6
3
∴DE=4
3
又∵Rt△ODE中,∠E=30° ∴∠DOE=60° ∴ S阴影=
??
△??????
?S扇形OAD=
1
2
×4×4
3
-
60·π·
4
2
360
=8
3
-
8π
3
29.【答案】解:(Ⅰ)如图1中, / ∵PA是⊙O的切线, ∴OA⊥AP, ∴∠PAO=90°,∵∠P=20°, ∴∠AOC=90°﹣20°=70°, ∴∠B=
1
2
∠AOC=35°, ∵OB=OC, ∴∠B=∠OCB=35°, ∴∠BCO=35°. (Ⅱ)如图2中,连接BD、OD. / ∵AD⊥OP于E, ∴AE=ED,
????
=
????
, ∵AE=ED,OA=OB, ∴OE=
1
2
DB, ∵OE=
1
2
CD, ∴CD=DB, ∴
????
=
????
, ∴
????
=
????
=
????
, ∴∠AOC=∠COD=∠BOD=60°, ∵PA是⊙O的切线, ∴∠PAO=90°, ∴∠P=30°
