浙江省丽江市青田二中2018 年秋九上数学期末复习汇编学案(A本,无答案)
文档属性
| 名称 | 浙江省丽江市青田二中2018 年秋九上数学期末复习汇编学案(A本,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-31 00:00:00 | ||
图片预览



文档简介
2018 年秋九上数学
青
田
二
中
数
学
期
末
复
习
汇
编
(A)
班级:___________ 姓名:______________
【基础篇】
第一章 二次函数
【知识结构】
1. 形如 y= (其中 a,b,c 是常数,a 0)的函数叫做二次函数,自变
量的取值范围是 .
2. 函数 y=a(x-m)2 +k(a≠0)的图象可由函数 y=ax2 的图象先向 (当 m>0)或向 (当
m<0)平移 个单位,再向 (当 k>0)或向 (当 k<0)平移 个单位得
到,顶点是 ,对称轴是 .
3. 二次函数 y=ax2+bx+c(a≠0)的图象是一条 ,它的对称轴是直线 ,
顶点坐标是 ,当 a>0 时,抛物线的开口 ,顶点是抛物线上的 ;
当 a<0 时,抛物线的开口 ,顶点是抛物线上的 .
【例题解析】
例 1 已知 12)2( ???? xxmy m 是 y 关于 x 的二次函数,则 m 的值为 .
练习
已知函数
222 2)( ???? mmxmmy
(1)当此函数是二次函数时,m= ,此时的函数表达式为 .
(2)当此函数是一次函数时,m= ,此时的函数表达式为 .
例 2.如图,已知二次函数 y=x2+bx+c过点 A(1,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点 P使△ABP的面积为 10,请直接写出点 P的坐标.
练习
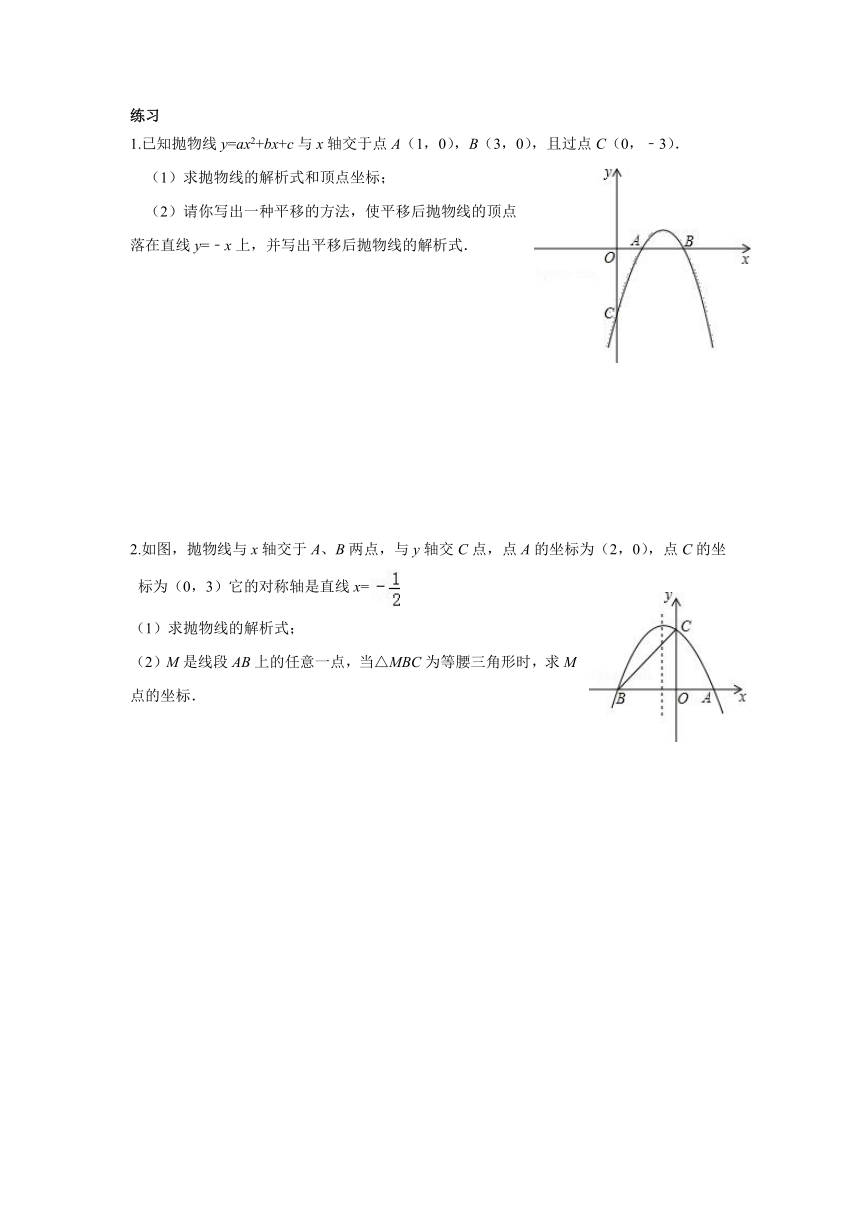
1.已知抛物线 y=ax2+bx+c与 x轴交于点 A(1,0),B(3,0),且过点 C(0,﹣3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点
落在直线 y=﹣x上,并写出平移后抛物线的解析式.
2.如图,抛物线与 x轴交于 A、B两点,与 y轴交 C点,点 A的坐标为(2,0),点 C的坐
标为(0,3)它的对称轴是直线 x=
(1)求抛物线的解析式;
(2)M是线段 AB上的任意一点,当△MBC为等腰三角形时,求 M
点的坐标.
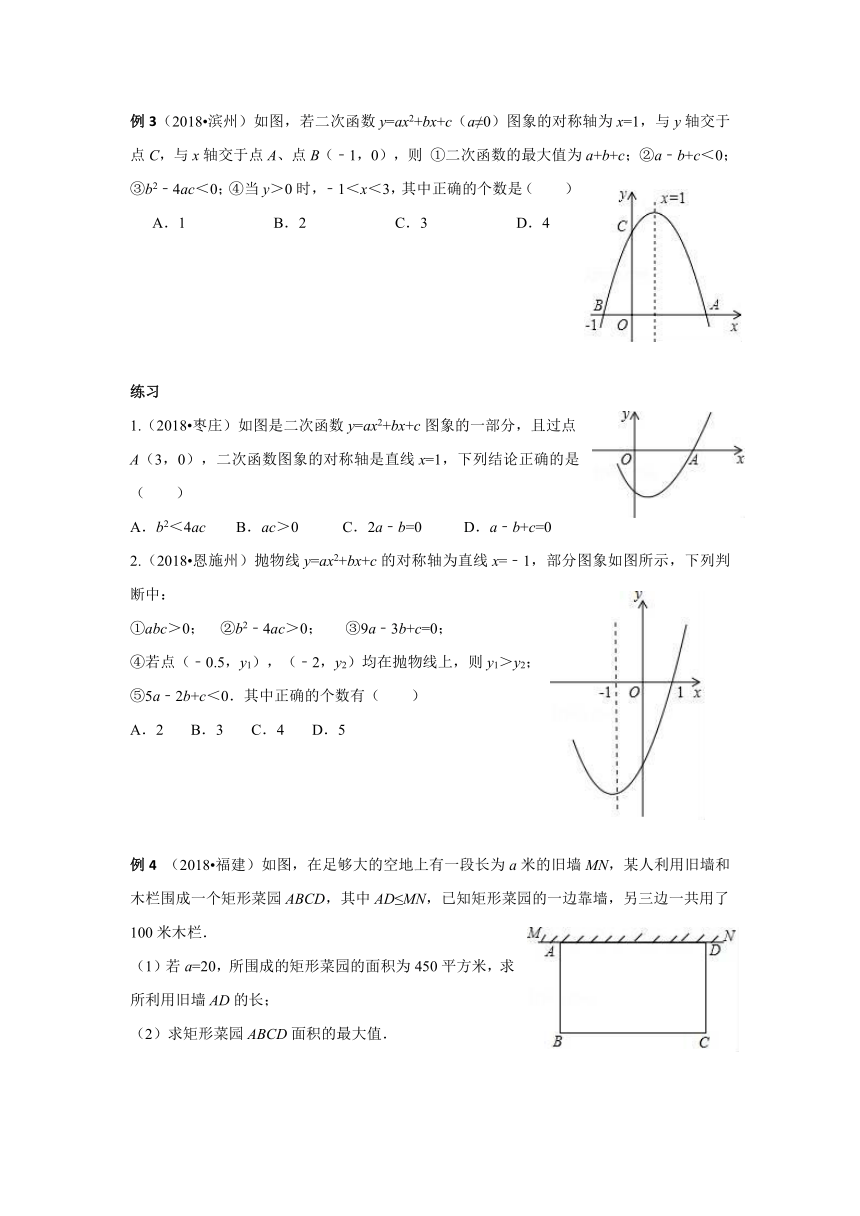
例 3(2018?滨州)如图,若二次函数 y=ax2+bx+c(a≠0)图象的对称轴为 x=1,与 y轴交于
点 C,与 x轴交于点 A、点 B(﹣1,0),则 ①二次函数的最大值为 a+b+c;②a﹣b+c<0;
③b2﹣4ac<0;④当 y>0时,﹣1<x<3,其中正确的个数是( )
A.1 B.2 C.3 D.4
练习
1.(2018?枣庄)如图是二次函数 y=ax2+bx+c图象的一部分,且过点
A(3,0),二次函数图象的对称轴是直线 x=1,下列结论正确的是
( )
A.b2<4ac B.ac>0 C.2a﹣b=0 D.a﹣b+c=0
2.(2018?恩施州)抛物线 y=ax2+bx+c的对称轴为直线 x=﹣1,部分图象如图所示,下列判
断中:
①abc>0; ②b2﹣4ac>0; ③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则 y1>y2;
⑤5a﹣2b+c<0.其中正确的个数有( )
A.2 B.3 C.4 D.5
例 4 (2018?福建)如图,在足够大的空地上有一段长为 a米的旧墙 MN,某人利用旧墙和
木栏围成一个矩形菜园 ABCD,其中 AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了
100米木栏.
(1)若 a=20,所围成的矩形菜园的面积为 450平方米,求
所利用旧墙 AD的长;
(2)求矩形菜园 ABCD面积的最大值.
练习
1.(2018?淮安)某景区商店销售一种纪念品,每件的进货价为 40元.经市场调研,当该纪
念品每件的销售价为 50元时,每天可销售 200件;当每件的销售价每增加 1元,每天的销
售数量将减少 10件.
(1)当每件的销售价为 52元时,该纪念品每天的销售数量为 件;
(2)当每件的销售价 x为多少时,销售该纪念品每天获得的利润 y最大?并求出最大利润.
2.一列火车在 A城的正北 240 km 处,以 120 km/h的速度驶向 A城.同时,一辆汽车在 A
城的正东 120 km处,以 120 km/h 速度向正西方向行驶.假设
火车和汽车的行驶方向和速度都保持不变,问何时火车与汽
车之间的距离最近?当火车与汽车距离最近时,汽车是否已
过铁路与公路的交叉口?
作业:
1. 抛物线 2xy ? 向右平移 2 个单位,再向上平移 3 个单位,得到的抛物线的解析式为( )
A. 3)2( 2 ??? xy B. 3)2( 2 ??? xy C. 3)2( 2 ??? xy D. 3)2( 2 ??? xy
2. 若抛物线 cxxy ??? 22 的顶点在 x轴上,则 c的值为( )
A. 1 B. -1 C. 2 D. 4
3.已知二次函数 cbxaxy ??? 2 的图象过点 A(1,2),B(3,2),C(5,7).若点 M(-
2,y1),N((-1,y2),K(8,y3)也在二次函数 cbxaxy ??? 2 的图象上,则下列结论
正确的是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y1<y3<y2
4.知二次函数 )0(2 ???? acbxaxy 的图象如图所示,则下列结
论:(1)4a+2b+c>0(2)方程 02 ??? cbxax 两根之和小于零 (3)
y随 x的增大而增大(4)一次函数 bcxy ?? 的图象一定不过第二
象限,其中正确的个数是 ( )
A、 4 个 B、 3 个 C、2 个 D、1 个
5.抛物线 ? ? 91 22 ???? kxky 开口向下,且经过原点,则 k =
6.抛物线 5)2(4 2 ???? xy 的对称轴是_________,顶点坐标是____.
7.已知二次函数 cbxxy ??? 2 的图象经过点(-1,0),(0,2),当 y随 x的增大而增大时,
x的取值范围是 ______
8.(2018?乌鲁木齐)把拋物线 y=2x
2
﹣4x+3 向左平移 1 个单位长度,得到的抛物线的解析
式为 .
9.(2018?宁波)已知抛物线 y=﹣ x2+bx+c经过点(1,0),(0, ).
(1)求该抛物线的函数表达式;
(2)将抛物线 y=﹣ x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平
移后的函数表达式.
2
O
x
y
10.(2018?黄冈)已知直线 l:y=kx+1与抛物线 y=x2﹣4x.
(1)求证:直线 l与该抛物线总有两个交点;
(2)设直线 l与该抛物线两交点为 A,B,O为原点,当 k=﹣2时,求△OAB的面积.
11.(2018?衢州)某游乐园有一个直径为 16 米的圆形喷水池,喷水池的周边有
一圈喷水头,喷出的水柱为抛物线,在距水池中心 3 米处达到最高,高度为 5
米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平
方向为 x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高
1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状
不变的前提下,把水池的直径扩大到 32米,各方向喷出的水柱仍在喷水池中心
保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
第三章 圆的基本性质
【知识结构】
1.如果 P 是圆所在平面内的一点,d 表示 P 到圆心的距离,r 表示圆的半径,则 d圆______;d___r,则 p 在圆上;d>r,则 p 在圆____.
2.如图,用几何语言表示垂径定理及逆定理
3.如图,用几何语言表示圆心角定理及逆定理
4.如图,用几何语言表示圆周角定理
5.圆内接四边形的对角________.
6.弧长计算公式:___________________;扇形面积计算公式:________________________.
【例题解析】
例题 1 如图, AB是⊙O的直径,弦 CD⊥ AB于点
E , cmCDcmOC 8,5 ?? ,求 AE。
练习 如图,在⊙O 中,AE 是直径,半径 OC 垂直于弦 AB 于 D,连接 BE,
若 AB=2 7 ,CD=1,则 BE 的长是( )
A.5 B.6 C.7 D.8
例题 2 如图,四边形 ABCD 是菱形,⊙O经过点 A,C,D 与 BC 相交于
点 E,连接 AC,AE,若∠D=78°,求∠EAC.[来源∶Z&xx&k.Com]
练习 如图,已知 AB 是⊙O 的弦,半径 OC 垂直 AB,点 D 是⊙O 上一点,
且点 D 与点 C 位于弦 AB 两侧,连接 AD、CD、OB,若∠BOC=70°,求∠
ADC.
例题 3 如图,△ABC 是⊙O 的内接三角形,AB=AC,∠BCA=65°,作 CD
∥AB,并与⊙O 相交于点 D,连接 BD,求∠DBC 的大小
练习 如图,点 A B C、 、 为 O? 上的三个点,
02 , 40BOC AOB BAC? ? ? ? ? ,则 ACB? ? ________度.
例题 4 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所
用的经验公式是:弧田面积=
1
2
(弦×矢+矢 2).弧田(如图阴影部
分),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,
“矢”等于半径长与圆心到弦的距离之差,现有圆心角为 120°,
半径等于 4 米的弧田,按照上述公式计算出弧田的面积为______
米 2.
练习 如图,⊙O是 ABC? 的外接圆, 2?BC , 030??BAC ,求劣弧 BC的长.
【作业】
1. 如图,AB 是⊙O 的直径,弦 CD⊥AB 于点 E,若 AB=8,AE=1,则弦 CD 的长是( )
A. 7 B.2 7 C.6 D.8
2.如图,?ABC 内接于⊙O,∠A=60°,BC=6 3,则?BC的长为( )
A.2? B.4? C.8? D.12?
3.如图,BC 是⊙O 的直径,点 A 在圆上,连接 AO,AC,∠AOB=64°,则∠ACB= 度.
4.如图,在圆内接四边形 ABCD 中,若∠A、∠B、∠C 的度数之比为 4∶3∶5,则∠D 的度数
是________ ?.
A
O
B
D
C
C
D
A
B
O
5.如图, ABC△ 内接于 O⊙ ,若 32OAB =∠ °,则 C =∠ .
6.如图,点 A,B,C 均在 6×6 的正方形网格格点上,过 A ,B ,C 三点的外接圆除经过 A,B,
C 三点外还能经过的格点数为 .
7.如图,四边形 ABCD 是⊙O 的内接四边形,点 D 是AC⌒的中点,点 E 是BC⌒上的一点,若∠
CED=40°,求∠ADC.
8.已知? O 的半径为 10cm,AB,CD是? O 的两条弦, / /AB CD,AB=16cm,CD=12cm,
求弦 AB和CD之间的距离.
9.如图,四边形 ABCD 内接于⊙O,AB 是⊙O 的直径,点 P 在 CA 的延长线上,∠CAD=45°.
若 AB=4,求
︵
CD的长;
第五章 解直角三角形
【知识结构】
1. 锐角三角函数的定义
如图所示,在 Rt△ABC 中,⑴sInA= ⑵coSA=
⑶tanA= ,锐角 A 的正弦,余弦,正切统称为锐角 A 的三角函
数。
2. 特殊角的三角函数
锐角α
三角函数
30° 45° 60°
Sinα
Cosα
tanα
3. 解直角三角形
图形 已知条件 解法步骤
在 Rt△ABC中,
∠C=90°
两
边
两直角边(如 a,b)
①由 tanA=,
求∠A;
②∠B=90°-∠A;
③c=
斜边与一直
角边(如 c,a)
①由 sinA=,
求∠A;
②∠B=90°-∠A;
③b=
一
边
一
角
一直
角边
和一
锐角
一锐角一邻
边(如∠A,b)
①∠B=90°-∠A;
②a=b·tanA;
③c=
一锐角一对
边(如∠A,a)
①∠B=90°-∠A;
②b=;
③c=
斜边和一
锐角(如 c,∠A)
①∠B=90°-∠A;
②a=c·sinA;
③b=c·cosA
【例题解析】
例题 1 在 Rt△ABC 中,∠C=90°,AB=5,BC=3,则 tanA 的值是( )
A. 3/4 B. 4/3 C. 3/5 D. 4/5
练习 如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且 OP与 x轴正半轴的夹
角α的正切值是 43,则 sinα的值为( )
A. 4/5 B. 5/4 C. 3/5 D. 5/3
例题 2 在△ABC中,若 tanA=1,sinB=2√2,你认为最确切的判断是( )
A. △ABC是等腰三角形 B. △ABC是等腰直角三角形
C. △ABC是直角三角形 D. △ABC是一般锐角三角形.
练习 1. 在 Rt△ABC 中,∠C=90°,AB=2,BC=√3,则 sinA/2=___.
2.求下列各式的值:
(1)tan30°+2cos60°; (2)sin30°+sin245°-tan260°+cos245°.
(3)sin260°+cos60°-tan45°;(4)sin60°-cos45°+;
例题 3 在 Rt△ABC 中,∠C=90°,已知 a,b,c 分别是∠A,∠B,∠C 的对边,且 a=2 ,
b=6 ,解这个直角三角形
练习 在△ABC 中,∠C=90°,∠A,∠B,∠C 的对边分别为 a,b,c.若∠A=60°,c=
12,求 a 和 b.
例题 4如图,港口 A在观测站 O的正东方向,OA=40海里,某船从港
口 A出发,沿北偏东 15°方向航行半小时后到达 B处,此时从观测站
O 处测得该船位于北偏东 60°的方向。求该船航行的速度___.
练习 如图,电线杆 CD 的高度为 h,两根拉线 AC 与 BC 相互垂
直,∠CAB=α,则拉线 BC 的长度为(A、D. B 在同一条直线上)( )
A. h/sinα B. h/cosα C. h/tanα D. h/?cosα
【作业】
1. 下列式子错误的是( )
A.cos40°=sin50° B.tan15°·tan75°=1
C.sin225°+cos225°=1 D.sin60°=2sin30°
2. 将一张矩形纸片 ABCD(如图)那样折起,使顶点 C落在 C′处,测量得 AB=4,DE=8. 则
sin∠C′ED为( )
A. 2 B. 1/ 2 C. √2/2 D. √3/2
3. 已知直线 l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为 h,矩形
ABCD 的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则
tanα的值等于( )
A. 3/2 B. 3/4 C. 4/3 D. 2/3.
4. 如图,一艘海轮位于灯塔 P 的南偏东 70°方向的 M 处,它以每小时 40
海里的速度向正北方向航行,2小时后到达位于灯塔 P的北偏东 40°的N处,
则 N 处与灯塔 P 的距离为( )
A. 40海里 B. 60海里 C. 70海里 D. 80 海里
5. 如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接 AC,BD,若 AC=2,则 tanD 的值
是 。
6. 如图,在 Rt△ABC中,∠C=90°,∠A=30°,E为 AB上一点且
AE:EB=4:1,EF⊥AC于 F,连接 FB,则 tan∠CFB的值等于
7.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀
丽.现在塔底低于地面约 7 米,某校学生测得古塔的整体高度约为
40 米.其测量塔顶相对地面高度的过程如下:先在地面 A 处测得塔
顶的仰角为 30°,再向古塔方向行进 米后到达 处,在 处测得
塔顶的仰角为 45°(如图所示),那么 的值约为_________米( ,结果精确到 0.1).
8.如图,在△ABC 中,CD⊥AB,垂足为 D. 若
AB=12,CD=6,tanA=3/2,求 sinB+cosB 的值。
9. 如图,已知四边形 ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,
BC的延长线与 AD的延长线交于点 E.
(1)若∠A=60°,求 BC的长;(2)若 sinA=4/5,求 AD的长。
(注意:本题中的计算过程和结果均保留根号)
.
10.如图,在一斜坡坡顶A处的同一水平线上有一古塔,为测量塔高
BC,数学老师带领同学在坡脚P处测得斜坡的坡角为α,且
tanα=7/24,塔顶C处的仰角为30°,他们沿着斜坡攀行了50米,到达
坡顶A处,在A处测得塔顶C的仰角为60°? .
(1)求斜坡的高度AD;
(2)求塔高BC.
【提高篇】
第一章 二次函数
【知识结构】
1. 二次函数的图象与系数 a,b,c 的关系.
2. 利用二次函数求实际问题中的最值.
3. 二次函数与几何综合问题,如线段的最值、面积的最值、存在性问题等.
【例题精讲】
【例 1】 (2018?白银)如图是二次函数 y=ax2+bx+c(a,b,
c 是常数,a≠0)图象的一部分,与 x 轴的交点 A 在点(2,0)
和(3,0)之间,对称轴是 x=1.对于下列说法:
①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m 为
实数);⑤当﹣1<x<3 时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
【练习】
1.(2018?衡阳)如图,抛物线 y=ax2+bx+c 与 x 轴交于点 A(﹣1,0),
顶点坐标(1,n)与 y 轴的交点在(0,2),(0,3)之间(包含
端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣ ;③对于任意实数 m,a+b≥am2+bm 总
成立;④关于 x的方程 ax2+bx+c=n﹣1 有两个不相等的实数根.其中结论正确的个数为( )
A.1 个 B.2 个 C.3 个 D.4 个
2.(2018?荆门)二次函数 y=ax2+bx+c(a≠0)的大致图象如图所示,
顶点坐标为(﹣2,﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;
③若方程 a(x+5)(x﹣1)=﹣1 有两个根 x1和 x2,且 x1<x2,则﹣5
<x1<x2<1;④若方程|ax2+bx+c|=1 有四个根,则这四个根的和为﹣
4.其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4 个
【例 2】
(2018?天门)绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如
图,线段 EF、折线 ABCD 分别表示该有机产品每千克的销售价 y1(元)、生产成本 y2(元)
与产量 x(kg)之间的函数关系.
(1)求该产品销售价 y1(元)与产量 x(kg)之间的函数关系式;
(2)直接写出生产成本 y2(元)与产量 x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
【练习】
1.(2018?扬州)“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为 30 元
/件,每天销售 y(件)与销售单价 x(元)之间存在一次函数关系,如图所示.
(1)求 y 与 x 之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于 240 件,当销售单价
为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出 150
元给希望工程,为了保证捐款后每天剩余利润不低于 3600 元,试
确定该漆器笔筒销售单价的范围.
2.(2018?温州)温州某企业安排 65 名工人生产甲、乙两种产品,每人每天生产 2 件甲或 1
件乙,甲产品每件可获利 15 元.根据市场需求和生产经验,乙产品每天产量不少于 5 件,
当每天生产 5 件时,每件可获利 120 元,每增加 1 件,当天平均每件利润减少 2 元.设每天
安排 x人生产乙产品.
(1)根据信息填表
产品种类 每天工人数(人) 每天产量(件) 每件产品可获利润
(元)
甲 15
乙 x x
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多 550 元,求每件乙产品
可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相
等.已知每人每天可生产 1 件丙(每人每天只能生产一件产品),丙产品每件可获利 30 元,
求每天生产三种产品可获得的总利润 W(元)的最大值及相应的 x 值.
【例 3】
(2017 四川内江,28,12 分)如图,在平面直角坐标系中,抛物线 y=ax2+bx+c(a≠0)与
y 轴交于点 C(0,3),与 x 轴交于 A,B 两点,点 B 坐标为(4,0),抛物线的对称轴方程
为 x=1.
(1)求抛物线的解析式;
(2)点 M 从 A 点出发,在线段 AB 上以每秒 3 个单位长度
的速度向 B 点运动,同时点 N 从 B 点出发,在线段 BC 上以
每秒 1 个单位长度的速度向 C 点运动,其中一个点到达终点
时,另一个点也停止运动,设△MBN 的面积为 S,点 M 运
动时间为 t,试求 S 与 t 的函数关系,并求 S 的最大值;
(3)在点 M 运动过程中,是否存在某一时刻 t,使△MBN
为直角三角形?若存在,求出 t 的值;若不存在,请说明理
由.
【练习】
1.(2018.温州)如图,抛物线 2y ax bx? ? ( 0a ? )交 x轴正半轴于点 A,直线 2y x? 经
过抛物线的顶点 M.已知该抛物线的对称轴为直线 2x ? ,交 x轴于点 B.
(1)求 a,b的值.
(2)P 是第一象限内抛物线上的一点,且在对称轴的右侧,连结 OP,BP.设点 P 的横坐标
为m,△OBP 的面积为 S,记 SK
m
? ,求K关于m的函
数表达式及K的范围.
2.(2018.绍兴)巳知,点M 为二次函数 14)( 2 ????? bbxy 图象的顶点,直线 5?? mxy
分别交 x轴, y 轴于点 BA,
(1)判断顶点M 是否在直线 14 ?? xy 上,并说明理由.
(2)如图 1.若二次函数图象也经过点 BA, .且 14)(5 2 ?????? bbxmx .根据图象,写出
x的取值范围.
(3)如图 2.点 A坐标为 )0,5( ,点M 在 BA0? 内,若点 ),
4
1( 1yC , ),4
3( 2yD 都在二次函数图
象上,试比较 1y 与 2y 的大小.
3.(2017 山东东营)
如图,直线 y=-
3
3
x+ 3分别与 x 轴、y 轴交于 B、C 两点,点 A 在 x 轴上,∠ACB=90°,
抛物线 y=ax2+bx+ 3经过 A、B 两点.
(1)求 A、B 两点的坐标;
(2)求抛物线的解析式;
(3)点 M 是直线 BC 上方抛物线上的一点,过点
M 从作 MH⊥BC 于点 H,作轴 MD∥y 轴交 BC 于点
D,求△DMH 周长的最大值.
4.(2017 湖南岳阳)
如图,抛物线 2
2
3
y x bx c? ? ? 经过点 ? ?3,0B , ? ?0, 2C ? ,直线 l: 2 2
3 3
y x? ? ? 交 y 轴于点 E,
且与抛物线交于 A,D 两点.P 为抛物线上一动点(不与 A,D 重合).
(1) 求抛物线的解析式;
(2) 当点 P 在直线 l 下方时,过点 P 作 PM x∥ 轴交 l 于点 M,PN y∥ 轴交 l 于点 N.求
PM PN? 的最大值;
(3) 设 F 为直线 l 上的点,以 E,C,P,F 为顶点的四边形能否构成平行四边形?若能,
求出点 F 的坐标;若不能,请说明理由.
C
D
H
A B
M
O
y
x
第三章 圆的基本性质
1.半角模型:是指从角的顶点向角的内部引出两条直线,这两条直线形成的夹
角恰好等于原角的一半。
如图,正方形 ABCD 中,E,F分别是 BC,CD 上的点,连结 AE,AF 分别交对角线 BD
于 M,N,且∠EAF=45度,连结 MF,EN.请证明下述结论:
(1) BE+DF=EF;
(2)S⊿ABE+S⊿ADF=S⊿AEF; S⊿AMN=S 四边形MNFE;
(3)C⊿ECF=2AB; (4)BM2+DN2=MN2
(5)⊿AEN 和⊿AFM都是等腰直角三角形;
(6)⊿AMN∽⊿DNF∽⊿BEM∽⊿AEF∽⊿BNA∽⊿DAM
(7)A、M、F、D四点共圆,A、B、E、N也四点共圆,M、N、F、C、E五点
共圆;
(8)∠AEB=∠AEF,∠AFE=∠AFD
(9)设 BE=x,,则 EF=
1
12
?
?
x
x
还能继续发现新的结论吗?请写下来跟大家分享!
2. 四点共圆
四边形一组对角互补,则这个四边形的四个顶点共圆。
同底同侧等角的三角形,各顶点共圆。
例题 如图,BE,CD 是⊿ABC 的高,连结 DE.
(1) 求证 AE.AC=AB.AD;
(2) 若∠BAC=120度,点M为 BC的中点,
求 DE:DM的值。
变式:如图 1,正方形 ABCD 中,E 为 BC 上一动点(可与 B,C 重合),过 B 作 BG
⊥AE 于 G,延长 BG 至点 F,使∠CFB=45 度。
(1) 求证:AG=FG;
(2) 如图 2,延长 FC,AE 交于点 M,连结 DF,BM.若 C为 FM的中点,BM=10,
求 FD的长。
(3) 如图 3,当点 E 在 BC 上运动时,过点 C 作 CH⊥BF 于 H,若正方形边
长为 1,求 AG+CH+DF 的最大值和最小值。
3.托勒密定理
圆的内接凸四边形的两组对边乘积之和等于两条对角线的乘积
请证明此定理。如图,四边形 ABCD 内接于⊙O,
则 AC.BD=AB.CD+AD.BC;
变式:有逆定理请叙述并证明之。
4.圆与垂直弦:如图 1,在⊙O 中,
AB⊥CD,OH⊥BD,则 AC=2OH.
例 如图,已知半径为 52 的⊙O 内有互相垂
直的两条弦 AB,CD,相交于点 P.
(1) 求证:PA.PB=PC.PD
(2) 设 BC中点为 F,连结 FP并延长交 AD于 E,
求证:EF⊥AD;
(3) 若 AB=8,CD=6,求 OP 的长。
变式:如图,已知⊙O 的半径为 3,点 M为⊙O 内的一个定点,OM= 5 ,
AB,CD是⊙O 的两条互相垂直的弦,垂足为 M.
(1) 当 AB=4时,求四边形 ADBC 的面积;
(2) 当 AB 变化时,求四边形 ADBC 的面积的最大值。
5.“圆”领衔的综合题
例 如图,点 E是△ABC 的内心,AE 的延长线交 BC 于点 F,交△ABC 的外接圆⊙O 于点 D;
连接 BD,过点 D 作直线 DM,使∠BDM=∠DAC.
(1)求证:直线 DM 是⊙O 的切线;
(2)求证:DE2=DF·DA.
A
M D
B
O
E
F C
··
变式:如图,已知 AB 是⊙O 的直径,弦 CD 与直径 AB 相交于点 F.点 E 在⊙O 外,作直线
AE,且∠EAC=∠D.
(1)求证:直线 AE 是⊙O 的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD=3
4
,CF=10
3
,求 BF 的长.
练习:1.(2017 浙江丽水 22,10 分)如图,在 Rt△ABC 中,∠C=Rt∠,以 BC 为直径的⊙
O交 AB 于点 D,切线 DE 交 AC 于点 E.
(1)求证:∠A=∠ADE;
(2)若 AD=16,DE=10,求 BC 的长.
2. (2017 山东枣庄 19,8 分)如图,在△ABC 中,∠C=90°,∠BAC 的平分线交 BC 于点
D,点 O 在 AB 上,以点 O 为圆心,OA 为半径的圆恰好
经过点 D,分别交 AC,AB 于 E,F.
(1)试判断直线 BC 与⊙O 的位置关系,并说明理由;
(2)若 BD=2 ,BF=2,求阴影部分的面积(结果保
留π).
3. (2017 浙江金华,22,10 分)如图,已知:AB 是⊙O 的直径,点 C 在⊙O 上,CD 是⊙O
的切线,AD⊥CD 于点 D.E 是 AB 延长线上的一点,CE 交⊙O 于点 F,连接 OC,AC.
(1)求证:AC 平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE 的度数.
②若⊙O 的半径为 2 2 ,求线段 EF 的长
4. (2017 山东聊城,10 分)如图, O? 是 ABC? 的外接圆,O点在 BC边上, BAC? 的
平分线交 O? 于点D,连接 ,BD CD,过点D作 BC的平行线,与 AB的延长线相交于点 P .
(1)求证: PD是 O? 的切线;
(2)求证: PBD DCA? ?∽ ;
(3)当 6, 8AB AC? ? 时,求线段PB的长.
第五章 解直角三角形
类型一 构造直角三角形的策略
例1 (2017丽水) 如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠
BOD=70
?
,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70? ≈
0.94,cos70
?
≈0.34,tan70
?
≈2.75)
变式(重庆中考) 如图,已知点 C与某建筑物底端 B相聚 306米(点 C与点 B在同一水平
面上),某同学从点 C出发,沿同一剖面的斜坡 CD行走 195米至坡顶 D处。斜坡 CD的坡
度(或坡比)i=1:2.4,在 D处测得该建筑物顶端 A的俯角为 20°,则建筑物 AB的高度约为(精
确到 0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)
A.29.1米 B.31.9米
C.45.9米 D.95.9米
类型二 等角转化的策略
例2 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sinB=AD/AB B.sinB=AC/BC
C.sinB=AD/AC D.sinB=CD/AC
变式 如图,15个形状大小完全相同的菱形组成网格,菱形的
顶点称为格点。已知菱形的一个角为60
?
,A. B. C都在格点上,点D在过A. B. C三点的圆弧
上,若E也在格点上,且∠AED=∠ACD,则cos∠AEC=___.
类型三 等边或等比转化的策略
例3(深圳中考) 如图,学校环保社成员想测量斜坡CD旁一棵树AB
的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得
树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树
AB的高度是( )m.
A. 20√3 B. 30 C. 30√3 D. 40
变式 如图,AB是O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC
上。设∠PCB=α,∠POC=β.
求证:tanα? tanβ2=13.
作业】
1.Rt△ABC中,∠ABC=90°,以AB为直径作O交AC于D,作直径DE,连接BE,
若sin∠ACB=45,BC=6,则BE=( )
A. 6 B. 32/5 C. 24/5 D. 8
2.(抚顺中考)如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB
的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方
向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯
角∠A′NB为45°,则电视塔AB的高度为___米(结果保留根号).
3.(邵阳中考) 如图所示,运载火箭从地面L处垂直向上发射,当火箭
到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30? ,n
秒后,火箭到达B点,此时仰角是45? ,则火箭在这n秒中上升的高度是
___km.
4.(绍兴中考) 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼
的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之
间的距离AB=30m.
(1)求∠BCD的度数。
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:
tan20°≈0.36,tan18°≈0.32)
5.(衢州中考) 在直角坐标系中,过
原点O及点A(8,0),C(0,6)作矩形
OABC、连结OB,点D为OB的中点,点E
是线段AB上的动点,连结DE,作DF
⊥DE,交OA于点F,连结EF.已知点E
从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。
(1)如图1,当t=3时,求DF的长。
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明
理由;如果不变,请求出tan∠DEF的值。
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值。
【专题篇】
专题:绝对值与数轴
【数轴与实际问题】
例 1 5个城市的国际标准时间(单位:时)在数轴上表示如下,那么北京时间 2006年 6月 17日上午
9时应是( )
A、伦敦时间 2006年 6月 17日凌晨 1时
B、纽约时间 2006年 6月 17日晚上 22时
C、多伦多时间 2006年 6月 16日晚上 20时
D、首尔时间 2006年 6月 17日上午 8时
例 2 在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所。已知青少年宫在学校
东 300米处,商场在学校西 200米处,医院在学校东 500米处。将马路近似地看成一条直线,以学校为
原点,以正东方向为正方向,用 1个单位长度表示 100米。
① 在数轴上表示出四家公共场所的位置。
② 计算青少年宫与商场之间的距离。
练习
1、如图,数轴上的点 P、O、Q、R、S表示某城市一条大街上的五个公交车站点,有一辆公交车距 P站
点 3km,距 Q站点 0.7km,则这辆公交车的位置在( )
A、R站点与 S站点之间 B、P站点与 O站点之间
C、O站点与 Q站点之间 D、Q站点与 R站点之间
2、老师在黑板上画数轴,取了原点 O后,用一个铁丝做的圆环作为工具,以圆环的直径在数轴上画出单
位长 1,再将圆环拉直成一线段,在数轴的正方向上以此线段长自原点 O起截得 A点,则 A点表示的
数是_____________。
【数轴与比较有理数的大小】
例 3 已知 a、b、c 在数轴上的位置如图。则在
1
a
? , a? , c b? , c a? 中,最大的一个是( )
A. a? B. c b? C. c a? D. 1
a
?
例 4 三个有理数 a、b、c 在数轴上的位置如图所示,则( )
A.
1 1 1
c a c b a b
? ?
? ? ?
B.
1 1 1
b c c a b a
? ?
? ? ?
练习
1、己知 a,b两数在数轴上对应的点如图所示,下列结论正确的是( )。
A. a b? B. 0ab ?
C. 0b a? ? D. 0a b? ?
2、如图,数轴上 A、B 两点分别对应实数 a、b则下列结论正确的是( )
A. 0a b? ? B. b a?
C. 0a b? ? D. 0a b? ?
3、若两个非零的有理数 a、b,满足:|a|=a,|b|=-b,a+b<0,则在数轴上表示数 a、b的点
正确的是( )
A、 B、
C、 D、
【寻找、判断数轴上的点】
例 5 如图,数轴上的 A、B、C三点所表示的数分别是 a、b、c,其中 AB=BC,如果|a|>|b|>|c|,
那么该数轴的原点 O的位置应该在( )
A、点 A的左边 B、点 A与点 B之间
C、点 B与点 C之间 D、点 B与点 C之间或点 C的右边
例 6 如图,数轴上标出若干点,每相邻的两点相距一个单位长度,点 A、B、C、D 对应的数分别为整数
a、b、c、d,且 2 4d a? ? 。试问:数轴上的原点在哪一点上?
练习
1、在数轴上,坐标是整数的点称为“整点”。设数轴的单位长度是 1厘米,若在这个数轴上随意画出一条
长 2008厘米的线段 AB, 则线段 AB 盖住的整点至少有_______个,至多有 个。
2、如图,数轴上标出若干个点,每相邻两点相距 1个单位,点 A、B、C、D 对应的整数 a、b、c、d,
且 2 9b a? ? ,那么数轴的原点对应点是( )。
A、A 点 B、B 点 C、C 点 D、D 点
3、如图所示,圆的周长为 4个单位长度,在圆的 4等分点处标上字母 A,B,C,D,先将圆周上的字母
A对应的点与数轴的数字 1所对应的点重合,若将圆沿着数轴向左滚动,那么数轴上的-2010所对应的
点将与圆周上字母所对应的点( )重合.
A B C DM N
a b c d
【与数轴有关的计算】
例 7 如图所示,在数轴上有六个点,点 F 所表示的数是8, 4AF ? 且 AB BC CD DE EF? ? ? ? ,
则与点C 所表示的数最接近的整数是 。
例 8 上午 8点,某人驾驶一辆汽车从 A地出发,向东记为正,向西记为负。记录前 4次行驶过程如下:
-15公里,+25公里,-20公里,+30公里,若要汽车最后回到 A地,则最后一次如何行驶?已知汽车
行驶的速度为 55千米/小时,在这期间他办事花去 2小时,问他回到 A地的时间?
练习
1、 如图,数轴上有 6个点,且相邻两点间的距离都相等,
则与 D点所表示的数最接近的整数是______。
2、某一电子昆虫落在数轴上的某点 0k ,从 0k 点开始跳动,第 1次向左跳 1个单位长度到 1k ,第 2次由 1k
向右跳 2个单位长度到 2k ,第 3次由 2k 向左跳 3个单位长度到 3k ,第 4次由 3k 向右跳 4个单位长度到 4k ,
依此规律跳下去,当它跳第 100次落下时,电子昆虫在数轴上的落点 100k 表示的数恰好是 2010,则电子
昆虫的初始位置 0k 所表示的数是___________。
3、一青蛙要从 A点跳到 B点,以平均每分钟 2米的速度跳跃。它先前进 1米,再后退 2米,又前进 3米,
再后退 4米,…(每次跳跃都在 A、B两点所在的直线上)
(1)5分钟后它离 A点多远?
(2)若 A、B两点相距 100米,它可能到达 B点吗?如果能,它第一次到达 B点需要多长时间?如果不
能,请说明理由。
三、利用数轴,深入认识绝对值
例 9 观察下列每对数在数轴上的对应点间的距离 4与-2,3与 5,-2与-6,-4与 3。
并回答下列各题:
(1)你能发现所得距离与这两个数的差的绝对值有什么关系吗?____________
(2)| x |的几何意义是数轴上表示_______的点与________之间的距离;
按照(1)的理解,| x |_________| x-0|(>, ?, <);
(3) 2 1? 的几何意义是数轴上表示 2的点与表示 1的点之间的距离;则 2 1? ? ____ ;
(4) 3x ? 的几何意义是数轴上表示 ___ 的点与表示 _____ 的点之间的距离,
若 3 1x ? ? ,则 x ? ________ ;
(5) 2x ? 的几何意义是数轴上表示 __ 的点与表示 _____ 的点之间的距离,
若 2 2x ? ? ,则 x ? ________ ;
例 10 m n? 的几何意义是数轴上表示m的点与表示 n的点之间的距离。
(1)当 1x ? ? 时,则 2 2x x? ? ? ? 。
(2)结合数轴求得 2 3x x? ? ? 的最小值为_____,取得最小值时 x的取值范围为___________。
(3)满足 341 ???? xx 的 x的取值范围为_________________。
练习
1、如图表示数轴上四个点的位置关系,且它们表示的数分别为 p , q, r , s。
若 10p r? ? , 12p s? ? , 9q s? ? ,则 q r? ? _______ 。
2、不相等的有理数 a,b, c在数轴上的对应点分别为 A,B,C,如果 a b b c a c? ? ? ? ? ,那
么点 A,B,C 在数轴上的位置关系是( )
A.点 A 在点 B,C 之间 B.点 B在点 A,C 之间
C.点C 在点 A,B 之间 D.以上三种情况均有可能
【2、利用数轴,绝对值化简】
例 11 知数 a、b、c在数轴上的位置如图所示,化简 a b a b b c? ? ? ? ? 的结果是( )。
A. 2 3a b c? ? B. 3b c?
C. b c? D. c b?
练习
1、 如图所示,根据数轴上给出的 a、b、c的条件,
试说明 a b b c a c? ? ? ? ? 的值与 c无关。
c0 ba
2、已知有理数 cba ,, 在数轴上的对应的位置如下图:则 bacac ?????1 化简后的结果是( )
A、 1?b B、 12 ?? ba C、 cba 221 ??? D、 bc ?? 21
3、已知 dcba ,,, 为有理数,在数轴上的位置如图所示:
且 ,64366 ???? dcba 求 cbabda ????? 22323 的值。
专题:数与式
知识精髓
对于代数式而言,求值与恒等变形的关系十分密切。一般情况下,代数式先化简后求值比较
方便。但是,有的代数式必须经过恒等变形以后,才能把代数式隐含的条件显现出来,进而
求出代数式的值。因此,求值中的方法技巧如下:
一、整体法:把问题或某些条件当成一个整体来处理
例 1 已知 0m
m
1
? 的值。
变式 1:若 m 为实数,且 3
1
??
m
m ,求
2
2 1
m
m ? 的值。
变式 2:设 a>b>0,a2+b2=4ab,求
ab
ba 22 ?
的值。
变式 3:已知 m 是方程 X2-2011x+1=0 的一个根,试求
1
2011
2010
2
2
?
??
m
mm 的值。
二、配方法:配成完全平方式,得到一元二次方程的根。
例 2 已知 a,b,c 是实数,求 12261412 ????????? cbacba
,求 a(c+b)+b(c+a)+c(a+b)的值。
变式 1:已知
2
1
1
??
???
ba
ba ,求以 a,b为边的等腰三角形的周长。
变式 2:已知实数 a,b,满足 a2+b2=ab+a+b-1,求 a+b 的值。
变式 3:已知实数满足 x2-2x+4y=5,试求 x+2y 的最大值。
三、换元法:把某个式子看成一个整体,用一个变量去代替它
例 3 计算:
??
?
?
??
?
?
?????
?
?
??
?
?
????????
?
?
??
?
?
??????
?
?
??
?
?
????
2010
1
...
3
1
2
1
2011
1
2010
1
...
3
1
2
1
1
2011
1
2010
1
...
3
1
2
1
2010
1
...
3
1
2
1
1
变式 1:解方程: 06
1
5
1
2
??
?
???
?
?
??
?
?
? x
x
x
x
变式 2:若实数 n 满足(n-44)2+(46-n)2=3,试求(n-44)(46-n)的值。
变式 3:已知关于 x的方程满足(x2+x)2-2(x2+x)-3=0,试求 x2+x 的值。
四、降次法:把含未知数的项的指数降低
例 4 已知 a 是 x2-3x+1=0 的根,试求
1
8252
2
2345
?
???
a
aaaa
的值.
变式 1:已知 x2-x-1=0,则代数式-x3+2x+2011 的值。
变式 2:a,b是一元二次方程 2x2-5x-3=0 的两根,求 2a2-4a+b 的值。
配套练习
1、已知 b 为正数,a 为 b 的小数部分,且 a2+b2=27,求 a+b 的值。
2、已知 4
4
??
a
b
b
a
,试求代数式
a
b
b
a
???
?
?
??
?
?
2
的值。
3、已知 A=a+2,B=a2-a+5,C=a2+5a-19,其中 a>2.
(1)判断 A 与 B 的大小关系;
(2)指出 A 与 C 哪个大?并说明理由。
4、已知 44
1
,
36
1
,
24
1
?
?
?
?
?
? ca
ac
cb
bc
ba
ab
,求 cabcab
abc
?? 的值。
5、若 m2-2m=1,求代数式 4m3-6m2-9m
m
1
? +2017 的值。
6、已知 a+b=4n+2,ab=1,若 19a2+155ab+19b2=2017,求 n 的值。
真题再现
1、已知 a-b-2=0,则 4ab-(a+b)2+7 的值= 。
2、若 a-x2=1,b-x2=2,c-x2=3,且 abc=2013.求
cbaab
c
ac
b
bc
a 111
????? 的值。
专题:判别式法解二次三项式
【知识结构】
判别式法,通过判别式解答问题,即对一元二次方程 ax2+bx+c=0(a≠0)判别式为? =b2-4ac,
当? >0 时,方程有两个不相等的实数根,当 ? =0 时,方程有两个相等的实数根;当? <0
时,方程没有实数根。判别式法在化简,构造求值,构造相关、证明题、综合应用等方面有
广泛应用。
【例题解析】
例题 1 已知关于 x 的方程 x2+2(m+1)x+m2+5=0 有两个不相等的实数根,化简:
441 2 ???? mmm
练习 若关于 x的方程(m-2)x2-2(m-1)x+m-3=0 有实数根,试讨论关于 x 的方程
(m-6)x2-2(m+1)x+m=0 的根的情况。
例题 2 已知 a,b,c 为△ABC 的三边,当 m>0 时,关于 x 的方程 c(x2+m)+b(x2-m)-2 m ax=0
有两个相等的实数根,试说明△ABC 的形状.
练习:如果一直角三角形的三边为 a, b, c,∠ B=90°,试判断关于 x 的方程
a(x2-1)-2cx+b(x2+1)=0 的根的情况。
例题 3 已知 x2-ax+3-b=0 有两个不相等的实数根,x2+(6-a)x+6-b=0 有两个相等的实数根,
x2+(4-a)x+5-b=0 无实数根,求 a,b 的取值范围;
练习:设两个方程 x2+4ax+4a2+a=0,x2+2 (a-1)x+a2=0 中至少有一个方程有实数根,求 a 的取
值范围。
例题 4 已知 x,y,z 为实数,且满足 0782 ???? xyzx 和 06622 ????? xyzzy ,求
证:1≤x≤9.
? ? 0)(
4
3)(22 ?????? caxcaxcb
练习 已知 x,y,z 为实数且满足 1??? zyx ,xy=z2-7z+14,在 z 为何值时, 22 yx ? 取
到最大值?最大值是多少?
【作业】
1. 若关于 a 的二次三项式 ka2+4a+1 是一个完全平方式,则 k 的值 ( )
A.1 B.2 C.4 D.
4
1
2.关于 x 的方程 02 ??? axx ,给出下列四个结论:
①存在实数 a,使得方程恰有 2 个不同的实根;
②存在实数 a,使得方程恰有 3 个不同的实根;
③存在实数 a,使得方程恰有 4 个不同的实根;
④存在实数 a,使得方程恰有 6 个不同的实根;
其中正确的结论个数是( )
A.1 B.2 C.3 D.4
3. 若 二 次 三 项 式 3x2-x+m 能 在 实 数 范 围 内 分 解 因 式 , 则 m 的 取 值 范 围
是: . .
4. 实数 x,y,z 满足 x+y +z=5,xy+yz+zx=3,则 z 的最大值是________.
5.已知 a,b,c为△ABC 的三边的长,方程
有两个相等的实数根,求证:△ABC 是等腰三角形。
6.若关于 x 的不等式组
?
?
?
??
??
23
2
ax
ax
有解,求函数
4
1)3( 2 ???? xxay 的图象与 x轴的交
点个数。
7.若 21 , xx 是关于 x 的方程 x2+bx+c=0 的两个实数根,且 kxx 221 ?? (k 是整数),则称方
程 x2+bx+c=0 为“偶系二次方程”,例如 x2-6x-27=0,x2-2x-8=0,x2+3x-
4
27
都是“偶系二次方程”;
(1)判断方程 x2+x-12=0 是否是“偶系二次方程”,并说明理由;
(2)对于任意一个整数 b,是否存在实数 c,使得关于 x 的方程 x2+bx+c=0 是“偶系二次方
程”,并说明理由。
8.已知实数 x,y,z 满足 x+y +z=0,xyz=2,求 zyx ?? 的最小值。
专题:不定方程
【知识结构】
不定方程(组)是指未知数的个数多于方程(组),其特点是它的解一般有多个,不能
唯一确定.
一、如何确定不定方程(组)的解?
不定方程(组)往往会给出限定条件,求的往往是不定方程(组)特殊解,如整数解、
正整数解、自然数解等等.
【例题解析】
例 1. 二元一次方程 2x+y=6 有 个解;有 个自然数解;有 个正整数解.
小结:求不定方程(组)的解,关键是看清题目要求,做到不漏不重.
练习 1.试试你的理解能力(求下例不定方程的正整数解):
(1) x+y=5; (2) 2x+3y=11; (1) 5x+2y=24; (2) 4x+3y=50.
例 2.适当提高:求方程 x+y+xy=2008 的正整数解.
小结:利用因式分解将不定方程转化为二元一次方程组求解.
练习 1.求方程 x
2
-y
2
=105 的正整数解.
练习 2.求方程(x+1)
2
+(y-2)
2
=1 的整数解有 组.
二、不定方程(组)的应用
不定方程(组)应用广泛,解决问题的关键是——充分挖掘题目隐含的条件,进而确定方
案.
例题.数学趣题:
我国古代数学家张建丘所著《算经》中的“百钱买百鸡”问题,鸡翁一,值钱五;
鸡母一,值钱三;鸡雏三,值钱一,百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?
【练习】
1. 假期到了,17 名女教师去外地培训,住宿时有 2 人间和 3 人间可供租住,若每个房间都
要住满,那么她们有几种租住方案( )
A.2 种 B.3 种 C.4 种 D.5 种
2. 地震期间为了紧急安置 60 名地震灾民,需要搭建可容纳 6 人或 4 人的帐篷,若所搭建
的帐篷恰好能容纳这 60 名灾民,则不同的搭建方案有( )
A.4 种 B.6 种 C.9 种 D.11 种
3.二中团委与社区联合举办“保护地球,人人有责”活动,选派 20 名学生分三组到 120 个
店铺发传单,若地一、二、三小组每人分别负责 8、6、5 个店铺,且每组店铺至少有两个
人,则学生分组方案有( )
A.3 种 B.4 种 C.5 种 D.6 种
4.现有球迷 150 人欲同时租用 A、B、C三种型号的客车去观看世界杯足球赛,其中 A、B、C
三种型号客车的载客量分别为 50 人、30 人、10 人,要求每辆车必须满载,其中 A型号客
车最多租两辆,则球迷们一次性达到赛场的租车方案有( )
A.3 种 B.4 种 C.5 种 D.6 种
5.小明决定买一些书包送给灾区的小朋友,超市中有 A、B、C 三种款式,其中 A 款每个 30
元,B款每个 40 元,C款每个 50 元,小明买了三款书包共 10 个,用了 400 元,问这三款
书包分别买了几个?
反思:若将题目中“小明买了三款书包共 10 个”改成“小明买了 10 个书包”,那么方案共
有哪几种?
6.某商场计划拨款 9 万元从厂家购进 50 台电视机,已知该厂生产甲、乙、丙三种不同型号
的电视机,出厂价分别为每台 1500 元、2100 元、2500 元.
(1) 某商场同时购进其中两种不同型号的电视机共 50 台,用去 9 万元,请你研究一下商
场的进货方案;
(2) 某商场销售一台甲,乙,丙型电视机分别可获利 150 元、200 元、250 元.在同时购
进两种不同型号电视机的方案中,为了使销售时获利最多,你选择哪种进货方案?
(3) 若商场准备用9万元同时购进这三种不同型号的电视机共50台,请你设计进货方案.
7.某车间共有 20 位工人,生产甲、乙、丙三种型号的零件,因受金融风暴 影响,该车间每
天只需生产甲、乙、丙三种零件共 50 件.如果丙型零件至少生产 3 件, 每人每天生产的零
件数与每个零件产值的数据如下表:
型号 每人每天生产零件数(件) 每个零件产值(元)
甲型 3 400
乙型 2 500
丙型 1 600
(1)问生产甲、乙、丙三种型号零件的工人分别有多少人?
(2)若使车间每天生产的产值最高,则生产三种型号零件的工人各有多少人?
三.解方程(组)拓展
【例题解析】
例 1.
? ?
12
1 2 5 22
4
x y z
x y z
x y
? ? ??
? ? ? ??
? ??
? ?
4 2 0
2 2 3
2 2 4
x y z
x y z
x y z
? ? ??
? ? ? ??
? ? ? ? ??
? ?
: : 1: 2 : 7
3
2 3 21
x y z
x y z
??
? ? ? ??
例 2.在实数范围内解下列方程或方程组:
【练习】解方程或方程组:
? ?
2 21 11 2 0
1
x x y
x
? ? ?
? ? ?
?
? ? 2 22 3 3 3 0x xy y x y? ? ? ? ? ?
? ? 2
2
3
2 4
x y z
xy z
? ? ??
?
? ??
? ?1 1 2 2 1 1 3 0x x y? ? ? ? ? ? ? ? 2 22 5 6 2 14 8 10 0x xy y x y? ? ? ? ? ?
? ?4 2 1 3 2 5 0x y x y? ? ? ? ? ?? ? ? ? ? ?2 23 1 4 8x y xy? ? ?
专题:含绝对值的函数
【知识结构】
1. 将含字母系数的绝对值方程转化为求函数图象的交点问题进行解决。
2. 通过数形结合思想和分类讨论思想解决字母系数的绝对值方程。
【例题解析】
例题 1 已知函数 y=∣x-2∣+1,当自变量 x 满足-1≤x≤m时,函数值 y的取值范围是 1≤y
≤4,则实数 m 的取值范围是: .
练习 : 已知函数 y=∣x-3∣-∣x+2∣,求 y 的最大值与最小值.
例题 2 设直线 y=ax+2 与函数 y=∣x-1∣-∣x-2∣+2 的图象交于三个不同的点,求实数 a的取
值范围。
练习 :方程 2x-1=a∣x-1∣有两个实数解,求实数 k 的取值范围。
例题 3 已知函数 f(x)= ∣8-2x-x2∣和一次函数 y=kx+k(k 为常数),这两个函数图象有( )
个交点。
练习 :若函数 y=b 的图象与函数 y= x2-3∣x-1∣-4x-3 的图象恰有三个交点,则 b 的可能值
为: 。
例题 4 已知函数 y=∣x2-2ax∣,其中 a 为常数
(1) 当 0≤x≤1 时,y 的最大值为 2,求 a的值;
(2) 若 a>0,当 0≤x≤2 时,y≤2,求 a 的取值范围;
(3) 当 a=-1 时,关于 x 的方程∣x2-2ax∣=m∣x-1∣有四个不同的实数解,求 m 的取值
范围。
练习:已知关于 x 的多项式 x2+bx+c,其中 b,c 是常数;
(1)当 b=2,c=-3 时,求多项式 x2+bx+c 的最小值;
(2)当 c=5 时,函数 y=x2+b∣x∣+c,若 y≥1,求 b 的取值范围;
(3)当 c=b2时,令 y=x2+bx+c,当 b≤x≤b+3 时,函数值 y 的最小值为 21,求此时二次函
数的解析式。
【作业】
1. 已知函数 y=∣x-1∣+∣x-5∣+∣x+2∣的最小值是( )
A.5 B. 6 C.7 D.8
2.已知 x 是正实数,则 y=∣x-1∣+∣2x-1∣+∣3x-1∣+∣4x-1∣+∣5x-1∣的 y最大值是
A.2 B. 3 C.4 D.5
3. 若方程∣x2-4x+3∣+ k=0 有三个根,则 k 的值是: 。
4.t 为常数,函数 y=∣x2-2x-t∣在 0≤y≤3上的最大值为 2,则 t的值: 。
5.已知如图所示,函数 )62(
3
1 2 ??? xxy 对应的曲线依次交 x轴正负半轴于点 A,B;
(1)求直线 y=
3
4
与该曲线所有交点的坐标;
(2)过点作两条互相垂直的直线分别交该曲线于点 C,D 两点,且点 C 落在 A 点右侧,D 点
落在 A,B 之间,若 AD=AC,求△ADC 的面积。
6.已知:关于 x 的方程 x 2 ? ( m ? 1) x ? m ? 2 ? 0 有两异号实数根 x1 , x2 ,且
x1> 2x ,若 x12 ? x22 ? 8 .
(1) 求 m 的值;
(2) 若函数 y ? x 2 ? bx ? c 的图像与 x 轴的两个交点的横坐标为 ? x1 ?1 ,
7. 已知关于 x 的多项式 x 2 -2|x-m|+1,其中 m 为常数.
(1)若 m=0,求方程 x
2
-2|x-m|+1=0 的根;
(2)令 y= x
2
-2|x-m|+1,当 0<m≤1 时,求 y 的最小值(用含 m 的代数式表示);
(3)若方程 x
2
-2|x-m|+1=1.5 恰有三个实数根,求 m 的值.
青
田
二
中
数
学
期
末
复
习
汇
编
(A)
班级:___________ 姓名:______________
【基础篇】
第一章 二次函数
【知识结构】
1. 形如 y= (其中 a,b,c 是常数,a 0)的函数叫做二次函数,自变
量的取值范围是 .
2. 函数 y=a(x-m)2 +k(a≠0)的图象可由函数 y=ax2 的图象先向 (当 m>0)或向 (当
m<0)平移 个单位,再向 (当 k>0)或向 (当 k<0)平移 个单位得
到,顶点是 ,对称轴是 .
3. 二次函数 y=ax2+bx+c(a≠0)的图象是一条 ,它的对称轴是直线 ,
顶点坐标是 ,当 a>0 时,抛物线的开口 ,顶点是抛物线上的 ;
当 a<0 时,抛物线的开口 ,顶点是抛物线上的 .
【例题解析】
例 1 已知 12)2( ???? xxmy m 是 y 关于 x 的二次函数,则 m 的值为 .
练习
已知函数
222 2)( ???? mmxmmy
(1)当此函数是二次函数时,m= ,此时的函数表达式为 .
(2)当此函数是一次函数时,m= ,此时的函数表达式为 .
例 2.如图,已知二次函数 y=x2+bx+c过点 A(1,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点 P使△ABP的面积为 10,请直接写出点 P的坐标.
练习
1.已知抛物线 y=ax2+bx+c与 x轴交于点 A(1,0),B(3,0),且过点 C(0,﹣3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点
落在直线 y=﹣x上,并写出平移后抛物线的解析式.
2.如图,抛物线与 x轴交于 A、B两点,与 y轴交 C点,点 A的坐标为(2,0),点 C的坐
标为(0,3)它的对称轴是直线 x=
(1)求抛物线的解析式;
(2)M是线段 AB上的任意一点,当△MBC为等腰三角形时,求 M
点的坐标.
例 3(2018?滨州)如图,若二次函数 y=ax2+bx+c(a≠0)图象的对称轴为 x=1,与 y轴交于
点 C,与 x轴交于点 A、点 B(﹣1,0),则 ①二次函数的最大值为 a+b+c;②a﹣b+c<0;
③b2﹣4ac<0;④当 y>0时,﹣1<x<3,其中正确的个数是( )
A.1 B.2 C.3 D.4
练习
1.(2018?枣庄)如图是二次函数 y=ax2+bx+c图象的一部分,且过点
A(3,0),二次函数图象的对称轴是直线 x=1,下列结论正确的是
( )
A.b2<4ac B.ac>0 C.2a﹣b=0 D.a﹣b+c=0
2.(2018?恩施州)抛物线 y=ax2+bx+c的对称轴为直线 x=﹣1,部分图象如图所示,下列判
断中:
①abc>0; ②b2﹣4ac>0; ③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则 y1>y2;
⑤5a﹣2b+c<0.其中正确的个数有( )
A.2 B.3 C.4 D.5
例 4 (2018?福建)如图,在足够大的空地上有一段长为 a米的旧墙 MN,某人利用旧墙和
木栏围成一个矩形菜园 ABCD,其中 AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了
100米木栏.
(1)若 a=20,所围成的矩形菜园的面积为 450平方米,求
所利用旧墙 AD的长;
(2)求矩形菜园 ABCD面积的最大值.
练习
1.(2018?淮安)某景区商店销售一种纪念品,每件的进货价为 40元.经市场调研,当该纪
念品每件的销售价为 50元时,每天可销售 200件;当每件的销售价每增加 1元,每天的销
售数量将减少 10件.
(1)当每件的销售价为 52元时,该纪念品每天的销售数量为 件;
(2)当每件的销售价 x为多少时,销售该纪念品每天获得的利润 y最大?并求出最大利润.
2.一列火车在 A城的正北 240 km 处,以 120 km/h的速度驶向 A城.同时,一辆汽车在 A
城的正东 120 km处,以 120 km/h 速度向正西方向行驶.假设
火车和汽车的行驶方向和速度都保持不变,问何时火车与汽
车之间的距离最近?当火车与汽车距离最近时,汽车是否已
过铁路与公路的交叉口?
作业:
1. 抛物线 2xy ? 向右平移 2 个单位,再向上平移 3 个单位,得到的抛物线的解析式为( )
A. 3)2( 2 ??? xy B. 3)2( 2 ??? xy C. 3)2( 2 ??? xy D. 3)2( 2 ??? xy
2. 若抛物线 cxxy ??? 22 的顶点在 x轴上,则 c的值为( )
A. 1 B. -1 C. 2 D. 4
3.已知二次函数 cbxaxy ??? 2 的图象过点 A(1,2),B(3,2),C(5,7).若点 M(-
2,y1),N((-1,y2),K(8,y3)也在二次函数 cbxaxy ??? 2 的图象上,则下列结论
正确的是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y1<y3<y2
4.知二次函数 )0(2 ???? acbxaxy 的图象如图所示,则下列结
论:(1)4a+2b+c>0(2)方程 02 ??? cbxax 两根之和小于零 (3)
y随 x的增大而增大(4)一次函数 bcxy ?? 的图象一定不过第二
象限,其中正确的个数是 ( )
A、 4 个 B、 3 个 C、2 个 D、1 个
5.抛物线 ? ? 91 22 ???? kxky 开口向下,且经过原点,则 k =
6.抛物线 5)2(4 2 ???? xy 的对称轴是_________,顶点坐标是____.
7.已知二次函数 cbxxy ??? 2 的图象经过点(-1,0),(0,2),当 y随 x的增大而增大时,
x的取值范围是 ______
8.(2018?乌鲁木齐)把拋物线 y=2x
2
﹣4x+3 向左平移 1 个单位长度,得到的抛物线的解析
式为 .
9.(2018?宁波)已知抛物线 y=﹣ x2+bx+c经过点(1,0),(0, ).
(1)求该抛物线的函数表达式;
(2)将抛物线 y=﹣ x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平
移后的函数表达式.
2
O
x
y
10.(2018?黄冈)已知直线 l:y=kx+1与抛物线 y=x2﹣4x.
(1)求证:直线 l与该抛物线总有两个交点;
(2)设直线 l与该抛物线两交点为 A,B,O为原点,当 k=﹣2时,求△OAB的面积.
11.(2018?衢州)某游乐园有一个直径为 16 米的圆形喷水池,喷水池的周边有
一圈喷水头,喷出的水柱为抛物线,在距水池中心 3 米处达到最高,高度为 5
米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平
方向为 x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高
1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状
不变的前提下,把水池的直径扩大到 32米,各方向喷出的水柱仍在喷水池中心
保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
第三章 圆的基本性质
【知识结构】
1.如果 P 是圆所在平面内的一点,d 表示 P 到圆心的距离,r 表示圆的半径,则 d
2.如图,用几何语言表示垂径定理及逆定理
3.如图,用几何语言表示圆心角定理及逆定理
4.如图,用几何语言表示圆周角定理
5.圆内接四边形的对角________.
6.弧长计算公式:___________________;扇形面积计算公式:________________________.
【例题解析】
例题 1 如图, AB是⊙O的直径,弦 CD⊥ AB于点
E , cmCDcmOC 8,5 ?? ,求 AE。
练习 如图,在⊙O 中,AE 是直径,半径 OC 垂直于弦 AB 于 D,连接 BE,
若 AB=2 7 ,CD=1,则 BE 的长是( )
A.5 B.6 C.7 D.8
例题 2 如图,四边形 ABCD 是菱形,⊙O经过点 A,C,D 与 BC 相交于
点 E,连接 AC,AE,若∠D=78°,求∠EAC.[来源∶Z&xx&k.Com]
练习 如图,已知 AB 是⊙O 的弦,半径 OC 垂直 AB,点 D 是⊙O 上一点,
且点 D 与点 C 位于弦 AB 两侧,连接 AD、CD、OB,若∠BOC=70°,求∠
ADC.
例题 3 如图,△ABC 是⊙O 的内接三角形,AB=AC,∠BCA=65°,作 CD
∥AB,并与⊙O 相交于点 D,连接 BD,求∠DBC 的大小
练习 如图,点 A B C、 、 为 O? 上的三个点,
02 , 40BOC AOB BAC? ? ? ? ? ,则 ACB? ? ________度.
例题 4 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所
用的经验公式是:弧田面积=
1
2
(弦×矢+矢 2).弧田(如图阴影部
分),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,
“矢”等于半径长与圆心到弦的距离之差,现有圆心角为 120°,
半径等于 4 米的弧田,按照上述公式计算出弧田的面积为______
米 2.
练习 如图,⊙O是 ABC? 的外接圆, 2?BC , 030??BAC ,求劣弧 BC的长.
【作业】
1. 如图,AB 是⊙O 的直径,弦 CD⊥AB 于点 E,若 AB=8,AE=1,则弦 CD 的长是( )
A. 7 B.2 7 C.6 D.8
2.如图,?ABC 内接于⊙O,∠A=60°,BC=6 3,则?BC的长为( )
A.2? B.4? C.8? D.12?
3.如图,BC 是⊙O 的直径,点 A 在圆上,连接 AO,AC,∠AOB=64°,则∠ACB= 度.
4.如图,在圆内接四边形 ABCD 中,若∠A、∠B、∠C 的度数之比为 4∶3∶5,则∠D 的度数
是________ ?.
A
O
B
D
C
C
D
A
B
O
5.如图, ABC△ 内接于 O⊙ ,若 32OAB =∠ °,则 C =∠ .
6.如图,点 A,B,C 均在 6×6 的正方形网格格点上,过 A ,B ,C 三点的外接圆除经过 A,B,
C 三点外还能经过的格点数为 .
7.如图,四边形 ABCD 是⊙O 的内接四边形,点 D 是AC⌒的中点,点 E 是BC⌒上的一点,若∠
CED=40°,求∠ADC.
8.已知? O 的半径为 10cm,AB,CD是? O 的两条弦, / /AB CD,AB=16cm,CD=12cm,
求弦 AB和CD之间的距离.
9.如图,四边形 ABCD 内接于⊙O,AB 是⊙O 的直径,点 P 在 CA 的延长线上,∠CAD=45°.
若 AB=4,求
︵
CD的长;
第五章 解直角三角形
【知识结构】
1. 锐角三角函数的定义
如图所示,在 Rt△ABC 中,⑴sInA= ⑵coSA=
⑶tanA= ,锐角 A 的正弦,余弦,正切统称为锐角 A 的三角函
数。
2. 特殊角的三角函数
锐角α
三角函数
30° 45° 60°
Sinα
Cosα
tanα
3. 解直角三角形
图形 已知条件 解法步骤
在 Rt△ABC中,
∠C=90°
两
边
两直角边(如 a,b)
①由 tanA=,
求∠A;
②∠B=90°-∠A;
③c=
斜边与一直
角边(如 c,a)
①由 sinA=,
求∠A;
②∠B=90°-∠A;
③b=
一
边
一
角
一直
角边
和一
锐角
一锐角一邻
边(如∠A,b)
①∠B=90°-∠A;
②a=b·tanA;
③c=
一锐角一对
边(如∠A,a)
①∠B=90°-∠A;
②b=;
③c=
斜边和一
锐角(如 c,∠A)
①∠B=90°-∠A;
②a=c·sinA;
③b=c·cosA
【例题解析】
例题 1 在 Rt△ABC 中,∠C=90°,AB=5,BC=3,则 tanA 的值是( )
A. 3/4 B. 4/3 C. 3/5 D. 4/5
练习 如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且 OP与 x轴正半轴的夹
角α的正切值是 43,则 sinα的值为( )
A. 4/5 B. 5/4 C. 3/5 D. 5/3
例题 2 在△ABC中,若 tanA=1,sinB=2√2,你认为最确切的判断是( )
A. △ABC是等腰三角形 B. △ABC是等腰直角三角形
C. △ABC是直角三角形 D. △ABC是一般锐角三角形.
练习 1. 在 Rt△ABC 中,∠C=90°,AB=2,BC=√3,则 sinA/2=___.
2.求下列各式的值:
(1)tan30°+2cos60°; (2)sin30°+sin245°-tan260°+cos245°.
(3)sin260°+cos60°-tan45°;(4)sin60°-cos45°+;
例题 3 在 Rt△ABC 中,∠C=90°,已知 a,b,c 分别是∠A,∠B,∠C 的对边,且 a=2 ,
b=6 ,解这个直角三角形
练习 在△ABC 中,∠C=90°,∠A,∠B,∠C 的对边分别为 a,b,c.若∠A=60°,c=
12,求 a 和 b.
例题 4如图,港口 A在观测站 O的正东方向,OA=40海里,某船从港
口 A出发,沿北偏东 15°方向航行半小时后到达 B处,此时从观测站
O 处测得该船位于北偏东 60°的方向。求该船航行的速度___.
练习 如图,电线杆 CD 的高度为 h,两根拉线 AC 与 BC 相互垂
直,∠CAB=α,则拉线 BC 的长度为(A、D. B 在同一条直线上)( )
A. h/sinα B. h/cosα C. h/tanα D. h/?cosα
【作业】
1. 下列式子错误的是( )
A.cos40°=sin50° B.tan15°·tan75°=1
C.sin225°+cos225°=1 D.sin60°=2sin30°
2. 将一张矩形纸片 ABCD(如图)那样折起,使顶点 C落在 C′处,测量得 AB=4,DE=8. 则
sin∠C′ED为( )
A. 2 B. 1/ 2 C. √2/2 D. √3/2
3. 已知直线 l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为 h,矩形
ABCD 的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则
tanα的值等于( )
A. 3/2 B. 3/4 C. 4/3 D. 2/3.
4. 如图,一艘海轮位于灯塔 P 的南偏东 70°方向的 M 处,它以每小时 40
海里的速度向正北方向航行,2小时后到达位于灯塔 P的北偏东 40°的N处,
则 N 处与灯塔 P 的距离为( )
A. 40海里 B. 60海里 C. 70海里 D. 80 海里
5. 如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接 AC,BD,若 AC=2,则 tanD 的值
是 。
6. 如图,在 Rt△ABC中,∠C=90°,∠A=30°,E为 AB上一点且
AE:EB=4:1,EF⊥AC于 F,连接 FB,则 tan∠CFB的值等于
7.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀
丽.现在塔底低于地面约 7 米,某校学生测得古塔的整体高度约为
40 米.其测量塔顶相对地面高度的过程如下:先在地面 A 处测得塔
顶的仰角为 30°,再向古塔方向行进 米后到达 处,在 处测得
塔顶的仰角为 45°(如图所示),那么 的值约为_________米( ,结果精确到 0.1).
8.如图,在△ABC 中,CD⊥AB,垂足为 D. 若
AB=12,CD=6,tanA=3/2,求 sinB+cosB 的值。
9. 如图,已知四边形 ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,
BC的延长线与 AD的延长线交于点 E.
(1)若∠A=60°,求 BC的长;(2)若 sinA=4/5,求 AD的长。
(注意:本题中的计算过程和结果均保留根号)
.
10.如图,在一斜坡坡顶A处的同一水平线上有一古塔,为测量塔高
BC,数学老师带领同学在坡脚P处测得斜坡的坡角为α,且
tanα=7/24,塔顶C处的仰角为30°,他们沿着斜坡攀行了50米,到达
坡顶A处,在A处测得塔顶C的仰角为60°? .
(1)求斜坡的高度AD;
(2)求塔高BC.
【提高篇】
第一章 二次函数
【知识结构】
1. 二次函数的图象与系数 a,b,c 的关系.
2. 利用二次函数求实际问题中的最值.
3. 二次函数与几何综合问题,如线段的最值、面积的最值、存在性问题等.
【例题精讲】
【例 1】 (2018?白银)如图是二次函数 y=ax2+bx+c(a,b,
c 是常数,a≠0)图象的一部分,与 x 轴的交点 A 在点(2,0)
和(3,0)之间,对称轴是 x=1.对于下列说法:
①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m 为
实数);⑤当﹣1<x<3 时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
【练习】
1.(2018?衡阳)如图,抛物线 y=ax2+bx+c 与 x 轴交于点 A(﹣1,0),
顶点坐标(1,n)与 y 轴的交点在(0,2),(0,3)之间(包含
端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣ ;③对于任意实数 m,a+b≥am2+bm 总
成立;④关于 x的方程 ax2+bx+c=n﹣1 有两个不相等的实数根.其中结论正确的个数为( )
A.1 个 B.2 个 C.3 个 D.4 个
2.(2018?荆门)二次函数 y=ax2+bx+c(a≠0)的大致图象如图所示,
顶点坐标为(﹣2,﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;
③若方程 a(x+5)(x﹣1)=﹣1 有两个根 x1和 x2,且 x1<x2,则﹣5
<x1<x2<1;④若方程|ax2+bx+c|=1 有四个根,则这四个根的和为﹣
4.其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4 个
【例 2】
(2018?天门)绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如
图,线段 EF、折线 ABCD 分别表示该有机产品每千克的销售价 y1(元)、生产成本 y2(元)
与产量 x(kg)之间的函数关系.
(1)求该产品销售价 y1(元)与产量 x(kg)之间的函数关系式;
(2)直接写出生产成本 y2(元)与产量 x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
【练习】
1.(2018?扬州)“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为 30 元
/件,每天销售 y(件)与销售单价 x(元)之间存在一次函数关系,如图所示.
(1)求 y 与 x 之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于 240 件,当销售单价
为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出 150
元给希望工程,为了保证捐款后每天剩余利润不低于 3600 元,试
确定该漆器笔筒销售单价的范围.
2.(2018?温州)温州某企业安排 65 名工人生产甲、乙两种产品,每人每天生产 2 件甲或 1
件乙,甲产品每件可获利 15 元.根据市场需求和生产经验,乙产品每天产量不少于 5 件,
当每天生产 5 件时,每件可获利 120 元,每增加 1 件,当天平均每件利润减少 2 元.设每天
安排 x人生产乙产品.
(1)根据信息填表
产品种类 每天工人数(人) 每天产量(件) 每件产品可获利润
(元)
甲 15
乙 x x
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多 550 元,求每件乙产品
可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相
等.已知每人每天可生产 1 件丙(每人每天只能生产一件产品),丙产品每件可获利 30 元,
求每天生产三种产品可获得的总利润 W(元)的最大值及相应的 x 值.
【例 3】
(2017 四川内江,28,12 分)如图,在平面直角坐标系中,抛物线 y=ax2+bx+c(a≠0)与
y 轴交于点 C(0,3),与 x 轴交于 A,B 两点,点 B 坐标为(4,0),抛物线的对称轴方程
为 x=1.
(1)求抛物线的解析式;
(2)点 M 从 A 点出发,在线段 AB 上以每秒 3 个单位长度
的速度向 B 点运动,同时点 N 从 B 点出发,在线段 BC 上以
每秒 1 个单位长度的速度向 C 点运动,其中一个点到达终点
时,另一个点也停止运动,设△MBN 的面积为 S,点 M 运
动时间为 t,试求 S 与 t 的函数关系,并求 S 的最大值;
(3)在点 M 运动过程中,是否存在某一时刻 t,使△MBN
为直角三角形?若存在,求出 t 的值;若不存在,请说明理
由.
【练习】
1.(2018.温州)如图,抛物线 2y ax bx? ? ( 0a ? )交 x轴正半轴于点 A,直线 2y x? 经
过抛物线的顶点 M.已知该抛物线的对称轴为直线 2x ? ,交 x轴于点 B.
(1)求 a,b的值.
(2)P 是第一象限内抛物线上的一点,且在对称轴的右侧,连结 OP,BP.设点 P 的横坐标
为m,△OBP 的面积为 S,记 SK
m
? ,求K关于m的函
数表达式及K的范围.
2.(2018.绍兴)巳知,点M 为二次函数 14)( 2 ????? bbxy 图象的顶点,直线 5?? mxy
分别交 x轴, y 轴于点 BA,
(1)判断顶点M 是否在直线 14 ?? xy 上,并说明理由.
(2)如图 1.若二次函数图象也经过点 BA, .且 14)(5 2 ?????? bbxmx .根据图象,写出
x的取值范围.
(3)如图 2.点 A坐标为 )0,5( ,点M 在 BA0? 内,若点 ),
4
1( 1yC , ),4
3( 2yD 都在二次函数图
象上,试比较 1y 与 2y 的大小.
3.(2017 山东东营)
如图,直线 y=-
3
3
x+ 3分别与 x 轴、y 轴交于 B、C 两点,点 A 在 x 轴上,∠ACB=90°,
抛物线 y=ax2+bx+ 3经过 A、B 两点.
(1)求 A、B 两点的坐标;
(2)求抛物线的解析式;
(3)点 M 是直线 BC 上方抛物线上的一点,过点
M 从作 MH⊥BC 于点 H,作轴 MD∥y 轴交 BC 于点
D,求△DMH 周长的最大值.
4.(2017 湖南岳阳)
如图,抛物线 2
2
3
y x bx c? ? ? 经过点 ? ?3,0B , ? ?0, 2C ? ,直线 l: 2 2
3 3
y x? ? ? 交 y 轴于点 E,
且与抛物线交于 A,D 两点.P 为抛物线上一动点(不与 A,D 重合).
(1) 求抛物线的解析式;
(2) 当点 P 在直线 l 下方时,过点 P 作 PM x∥ 轴交 l 于点 M,PN y∥ 轴交 l 于点 N.求
PM PN? 的最大值;
(3) 设 F 为直线 l 上的点,以 E,C,P,F 为顶点的四边形能否构成平行四边形?若能,
求出点 F 的坐标;若不能,请说明理由.
C
D
H
A B
M
O
y
x
第三章 圆的基本性质
1.半角模型:是指从角的顶点向角的内部引出两条直线,这两条直线形成的夹
角恰好等于原角的一半。
如图,正方形 ABCD 中,E,F分别是 BC,CD 上的点,连结 AE,AF 分别交对角线 BD
于 M,N,且∠EAF=45度,连结 MF,EN.请证明下述结论:
(1) BE+DF=EF;
(2)S⊿ABE+S⊿ADF=S⊿AEF; S⊿AMN=S 四边形MNFE;
(3)C⊿ECF=2AB; (4)BM2+DN2=MN2
(5)⊿AEN 和⊿AFM都是等腰直角三角形;
(6)⊿AMN∽⊿DNF∽⊿BEM∽⊿AEF∽⊿BNA∽⊿DAM
(7)A、M、F、D四点共圆,A、B、E、N也四点共圆,M、N、F、C、E五点
共圆;
(8)∠AEB=∠AEF,∠AFE=∠AFD
(9)设 BE=x,,则 EF=
1
12
?
?
x
x
还能继续发现新的结论吗?请写下来跟大家分享!
2. 四点共圆
四边形一组对角互补,则这个四边形的四个顶点共圆。
同底同侧等角的三角形,各顶点共圆。
例题 如图,BE,CD 是⊿ABC 的高,连结 DE.
(1) 求证 AE.AC=AB.AD;
(2) 若∠BAC=120度,点M为 BC的中点,
求 DE:DM的值。
变式:如图 1,正方形 ABCD 中,E 为 BC 上一动点(可与 B,C 重合),过 B 作 BG
⊥AE 于 G,延长 BG 至点 F,使∠CFB=45 度。
(1) 求证:AG=FG;
(2) 如图 2,延长 FC,AE 交于点 M,连结 DF,BM.若 C为 FM的中点,BM=10,
求 FD的长。
(3) 如图 3,当点 E 在 BC 上运动时,过点 C 作 CH⊥BF 于 H,若正方形边
长为 1,求 AG+CH+DF 的最大值和最小值。
3.托勒密定理
圆的内接凸四边形的两组对边乘积之和等于两条对角线的乘积
请证明此定理。如图,四边形 ABCD 内接于⊙O,
则 AC.BD=AB.CD+AD.BC;
变式:有逆定理请叙述并证明之。
4.圆与垂直弦:如图 1,在⊙O 中,
AB⊥CD,OH⊥BD,则 AC=2OH.
例 如图,已知半径为 52 的⊙O 内有互相垂
直的两条弦 AB,CD,相交于点 P.
(1) 求证:PA.PB=PC.PD
(2) 设 BC中点为 F,连结 FP并延长交 AD于 E,
求证:EF⊥AD;
(3) 若 AB=8,CD=6,求 OP 的长。
变式:如图,已知⊙O 的半径为 3,点 M为⊙O 内的一个定点,OM= 5 ,
AB,CD是⊙O 的两条互相垂直的弦,垂足为 M.
(1) 当 AB=4时,求四边形 ADBC 的面积;
(2) 当 AB 变化时,求四边形 ADBC 的面积的最大值。
5.“圆”领衔的综合题
例 如图,点 E是△ABC 的内心,AE 的延长线交 BC 于点 F,交△ABC 的外接圆⊙O 于点 D;
连接 BD,过点 D 作直线 DM,使∠BDM=∠DAC.
(1)求证:直线 DM 是⊙O 的切线;
(2)求证:DE2=DF·DA.
A
M D
B
O
E
F C
··
变式:如图,已知 AB 是⊙O 的直径,弦 CD 与直径 AB 相交于点 F.点 E 在⊙O 外,作直线
AE,且∠EAC=∠D.
(1)求证:直线 AE 是⊙O 的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD=3
4
,CF=10
3
,求 BF 的长.
练习:1.(2017 浙江丽水 22,10 分)如图,在 Rt△ABC 中,∠C=Rt∠,以 BC 为直径的⊙
O交 AB 于点 D,切线 DE 交 AC 于点 E.
(1)求证:∠A=∠ADE;
(2)若 AD=16,DE=10,求 BC 的长.
2. (2017 山东枣庄 19,8 分)如图,在△ABC 中,∠C=90°,∠BAC 的平分线交 BC 于点
D,点 O 在 AB 上,以点 O 为圆心,OA 为半径的圆恰好
经过点 D,分别交 AC,AB 于 E,F.
(1)试判断直线 BC 与⊙O 的位置关系,并说明理由;
(2)若 BD=2 ,BF=2,求阴影部分的面积(结果保
留π).
3. (2017 浙江金华,22,10 分)如图,已知:AB 是⊙O 的直径,点 C 在⊙O 上,CD 是⊙O
的切线,AD⊥CD 于点 D.E 是 AB 延长线上的一点,CE 交⊙O 于点 F,连接 OC,AC.
(1)求证:AC 平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE 的度数.
②若⊙O 的半径为 2 2 ,求线段 EF 的长
4. (2017 山东聊城,10 分)如图, O? 是 ABC? 的外接圆,O点在 BC边上, BAC? 的
平分线交 O? 于点D,连接 ,BD CD,过点D作 BC的平行线,与 AB的延长线相交于点 P .
(1)求证: PD是 O? 的切线;
(2)求证: PBD DCA? ?∽ ;
(3)当 6, 8AB AC? ? 时,求线段PB的长.
第五章 解直角三角形
类型一 构造直角三角形的策略
例1 (2017丽水) 如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠
BOD=70
?
,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70? ≈
0.94,cos70
?
≈0.34,tan70
?
≈2.75)
变式(重庆中考) 如图,已知点 C与某建筑物底端 B相聚 306米(点 C与点 B在同一水平
面上),某同学从点 C出发,沿同一剖面的斜坡 CD行走 195米至坡顶 D处。斜坡 CD的坡
度(或坡比)i=1:2.4,在 D处测得该建筑物顶端 A的俯角为 20°,则建筑物 AB的高度约为(精
确到 0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)
A.29.1米 B.31.9米
C.45.9米 D.95.9米
类型二 等角转化的策略
例2 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sinB=AD/AB B.sinB=AC/BC
C.sinB=AD/AC D.sinB=CD/AC
变式 如图,15个形状大小完全相同的菱形组成网格,菱形的
顶点称为格点。已知菱形的一个角为60
?
,A. B. C都在格点上,点D在过A. B. C三点的圆弧
上,若E也在格点上,且∠AED=∠ACD,则cos∠AEC=___.
类型三 等边或等比转化的策略
例3(深圳中考) 如图,学校环保社成员想测量斜坡CD旁一棵树AB
的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得
树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树
AB的高度是( )m.
A. 20√3 B. 30 C. 30√3 D. 40
变式 如图,AB是O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC
上。设∠PCB=α,∠POC=β.
求证:tanα? tanβ2=13.
作业】
1.Rt△ABC中,∠ABC=90°,以AB为直径作O交AC于D,作直径DE,连接BE,
若sin∠ACB=45,BC=6,则BE=( )
A. 6 B. 32/5 C. 24/5 D. 8
2.(抚顺中考)如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB
的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方
向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯
角∠A′NB为45°,则电视塔AB的高度为___米(结果保留根号).
3.(邵阳中考) 如图所示,运载火箭从地面L处垂直向上发射,当火箭
到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30? ,n
秒后,火箭到达B点,此时仰角是45? ,则火箭在这n秒中上升的高度是
___km.
4.(绍兴中考) 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼
的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之
间的距离AB=30m.
(1)求∠BCD的度数。
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:
tan20°≈0.36,tan18°≈0.32)
5.(衢州中考) 在直角坐标系中,过
原点O及点A(8,0),C(0,6)作矩形
OABC、连结OB,点D为OB的中点,点E
是线段AB上的动点,连结DE,作DF
⊥DE,交OA于点F,连结EF.已知点E
从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。
(1)如图1,当t=3时,求DF的长。
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明
理由;如果不变,请求出tan∠DEF的值。
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值。
【专题篇】
专题:绝对值与数轴
【数轴与实际问题】
例 1 5个城市的国际标准时间(单位:时)在数轴上表示如下,那么北京时间 2006年 6月 17日上午
9时应是( )
A、伦敦时间 2006年 6月 17日凌晨 1时
B、纽约时间 2006年 6月 17日晚上 22时
C、多伦多时间 2006年 6月 16日晚上 20时
D、首尔时间 2006年 6月 17日上午 8时
例 2 在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所。已知青少年宫在学校
东 300米处,商场在学校西 200米处,医院在学校东 500米处。将马路近似地看成一条直线,以学校为
原点,以正东方向为正方向,用 1个单位长度表示 100米。
① 在数轴上表示出四家公共场所的位置。
② 计算青少年宫与商场之间的距离。
练习
1、如图,数轴上的点 P、O、Q、R、S表示某城市一条大街上的五个公交车站点,有一辆公交车距 P站
点 3km,距 Q站点 0.7km,则这辆公交车的位置在( )
A、R站点与 S站点之间 B、P站点与 O站点之间
C、O站点与 Q站点之间 D、Q站点与 R站点之间
2、老师在黑板上画数轴,取了原点 O后,用一个铁丝做的圆环作为工具,以圆环的直径在数轴上画出单
位长 1,再将圆环拉直成一线段,在数轴的正方向上以此线段长自原点 O起截得 A点,则 A点表示的
数是_____________。
【数轴与比较有理数的大小】
例 3 已知 a、b、c 在数轴上的位置如图。则在
1
a
? , a? , c b? , c a? 中,最大的一个是( )
A. a? B. c b? C. c a? D. 1
a
?
例 4 三个有理数 a、b、c 在数轴上的位置如图所示,则( )
A.
1 1 1
c a c b a b
? ?
? ? ?
B.
1 1 1
b c c a b a
? ?
? ? ?
练习
1、己知 a,b两数在数轴上对应的点如图所示,下列结论正确的是( )。
A. a b? B. 0ab ?
C. 0b a? ? D. 0a b? ?
2、如图,数轴上 A、B 两点分别对应实数 a、b则下列结论正确的是( )
A. 0a b? ? B. b a?
C. 0a b? ? D. 0a b? ?
3、若两个非零的有理数 a、b,满足:|a|=a,|b|=-b,a+b<0,则在数轴上表示数 a、b的点
正确的是( )
A、 B、
C、 D、
【寻找、判断数轴上的点】
例 5 如图,数轴上的 A、B、C三点所表示的数分别是 a、b、c,其中 AB=BC,如果|a|>|b|>|c|,
那么该数轴的原点 O的位置应该在( )
A、点 A的左边 B、点 A与点 B之间
C、点 B与点 C之间 D、点 B与点 C之间或点 C的右边
例 6 如图,数轴上标出若干点,每相邻的两点相距一个单位长度,点 A、B、C、D 对应的数分别为整数
a、b、c、d,且 2 4d a? ? 。试问:数轴上的原点在哪一点上?
练习
1、在数轴上,坐标是整数的点称为“整点”。设数轴的单位长度是 1厘米,若在这个数轴上随意画出一条
长 2008厘米的线段 AB, 则线段 AB 盖住的整点至少有_______个,至多有 个。
2、如图,数轴上标出若干个点,每相邻两点相距 1个单位,点 A、B、C、D 对应的整数 a、b、c、d,
且 2 9b a? ? ,那么数轴的原点对应点是( )。
A、A 点 B、B 点 C、C 点 D、D 点
3、如图所示,圆的周长为 4个单位长度,在圆的 4等分点处标上字母 A,B,C,D,先将圆周上的字母
A对应的点与数轴的数字 1所对应的点重合,若将圆沿着数轴向左滚动,那么数轴上的-2010所对应的
点将与圆周上字母所对应的点( )重合.
A B C DM N
a b c d
【与数轴有关的计算】
例 7 如图所示,在数轴上有六个点,点 F 所表示的数是8, 4AF ? 且 AB BC CD DE EF? ? ? ? ,
则与点C 所表示的数最接近的整数是 。
例 8 上午 8点,某人驾驶一辆汽车从 A地出发,向东记为正,向西记为负。记录前 4次行驶过程如下:
-15公里,+25公里,-20公里,+30公里,若要汽车最后回到 A地,则最后一次如何行驶?已知汽车
行驶的速度为 55千米/小时,在这期间他办事花去 2小时,问他回到 A地的时间?
练习
1、 如图,数轴上有 6个点,且相邻两点间的距离都相等,
则与 D点所表示的数最接近的整数是______。
2、某一电子昆虫落在数轴上的某点 0k ,从 0k 点开始跳动,第 1次向左跳 1个单位长度到 1k ,第 2次由 1k
向右跳 2个单位长度到 2k ,第 3次由 2k 向左跳 3个单位长度到 3k ,第 4次由 3k 向右跳 4个单位长度到 4k ,
依此规律跳下去,当它跳第 100次落下时,电子昆虫在数轴上的落点 100k 表示的数恰好是 2010,则电子
昆虫的初始位置 0k 所表示的数是___________。
3、一青蛙要从 A点跳到 B点,以平均每分钟 2米的速度跳跃。它先前进 1米,再后退 2米,又前进 3米,
再后退 4米,…(每次跳跃都在 A、B两点所在的直线上)
(1)5分钟后它离 A点多远?
(2)若 A、B两点相距 100米,它可能到达 B点吗?如果能,它第一次到达 B点需要多长时间?如果不
能,请说明理由。
三、利用数轴,深入认识绝对值
例 9 观察下列每对数在数轴上的对应点间的距离 4与-2,3与 5,-2与-6,-4与 3。
并回答下列各题:
(1)你能发现所得距离与这两个数的差的绝对值有什么关系吗?____________
(2)| x |的几何意义是数轴上表示_______的点与________之间的距离;
按照(1)的理解,| x |_________| x-0|(>, ?, <);
(3) 2 1? 的几何意义是数轴上表示 2的点与表示 1的点之间的距离;则 2 1? ? ____ ;
(4) 3x ? 的几何意义是数轴上表示 ___ 的点与表示 _____ 的点之间的距离,
若 3 1x ? ? ,则 x ? ________ ;
(5) 2x ? 的几何意义是数轴上表示 __ 的点与表示 _____ 的点之间的距离,
若 2 2x ? ? ,则 x ? ________ ;
例 10 m n? 的几何意义是数轴上表示m的点与表示 n的点之间的距离。
(1)当 1x ? ? 时,则 2 2x x? ? ? ? 。
(2)结合数轴求得 2 3x x? ? ? 的最小值为_____,取得最小值时 x的取值范围为___________。
(3)满足 341 ???? xx 的 x的取值范围为_________________。
练习
1、如图表示数轴上四个点的位置关系,且它们表示的数分别为 p , q, r , s。
若 10p r? ? , 12p s? ? , 9q s? ? ,则 q r? ? _______ 。
2、不相等的有理数 a,b, c在数轴上的对应点分别为 A,B,C,如果 a b b c a c? ? ? ? ? ,那
么点 A,B,C 在数轴上的位置关系是( )
A.点 A 在点 B,C 之间 B.点 B在点 A,C 之间
C.点C 在点 A,B 之间 D.以上三种情况均有可能
【2、利用数轴,绝对值化简】
例 11 知数 a、b、c在数轴上的位置如图所示,化简 a b a b b c? ? ? ? ? 的结果是( )。
A. 2 3a b c? ? B. 3b c?
C. b c? D. c b?
练习
1、 如图所示,根据数轴上给出的 a、b、c的条件,
试说明 a b b c a c? ? ? ? ? 的值与 c无关。
c0 ba
2、已知有理数 cba ,, 在数轴上的对应的位置如下图:则 bacac ?????1 化简后的结果是( )
A、 1?b B、 12 ?? ba C、 cba 221 ??? D、 bc ?? 21
3、已知 dcba ,,, 为有理数,在数轴上的位置如图所示:
且 ,64366 ???? dcba 求 cbabda ????? 22323 的值。
专题:数与式
知识精髓
对于代数式而言,求值与恒等变形的关系十分密切。一般情况下,代数式先化简后求值比较
方便。但是,有的代数式必须经过恒等变形以后,才能把代数式隐含的条件显现出来,进而
求出代数式的值。因此,求值中的方法技巧如下:
一、整体法:把问题或某些条件当成一个整体来处理
例 1 已知 0
m
1
? 的值。
变式 1:若 m 为实数,且 3
1
??
m
m ,求
2
2 1
m
m ? 的值。
变式 2:设 a>b>0,a2+b2=4ab,求
ab
ba 22 ?
的值。
变式 3:已知 m 是方程 X2-2011x+1=0 的一个根,试求
1
2011
2010
2
2
?
??
m
mm 的值。
二、配方法:配成完全平方式,得到一元二次方程的根。
例 2 已知 a,b,c 是实数,求 12261412 ????????? cbacba
,求 a(c+b)+b(c+a)+c(a+b)的值。
变式 1:已知
2
1
1
??
???
ba
ba ,求以 a,b为边的等腰三角形的周长。
变式 2:已知实数 a,b,满足 a2+b2=ab+a+b-1,求 a+b 的值。
变式 3:已知实数满足 x2-2x+4y=5,试求 x+2y 的最大值。
三、换元法:把某个式子看成一个整体,用一个变量去代替它
例 3 计算:
??
?
?
??
?
?
?????
?
?
??
?
?
????????
?
?
??
?
?
??????
?
?
??
?
?
????
2010
1
...
3
1
2
1
2011
1
2010
1
...
3
1
2
1
1
2011
1
2010
1
...
3
1
2
1
2010
1
...
3
1
2
1
1
变式 1:解方程: 06
1
5
1
2
??
?
???
?
?
??
?
?
? x
x
x
x
变式 2:若实数 n 满足(n-44)2+(46-n)2=3,试求(n-44)(46-n)的值。
变式 3:已知关于 x的方程满足(x2+x)2-2(x2+x)-3=0,试求 x2+x 的值。
四、降次法:把含未知数的项的指数降低
例 4 已知 a 是 x2-3x+1=0 的根,试求
1
8252
2
2345
?
???
a
aaaa
的值.
变式 1:已知 x2-x-1=0,则代数式-x3+2x+2011 的值。
变式 2:a,b是一元二次方程 2x2-5x-3=0 的两根,求 2a2-4a+b 的值。
配套练习
1、已知 b 为正数,a 为 b 的小数部分,且 a2+b2=27,求 a+b 的值。
2、已知 4
4
??
a
b
b
a
,试求代数式
a
b
b
a
???
?
?
??
?
?
2
的值。
3、已知 A=a+2,B=a2-a+5,C=a2+5a-19,其中 a>2.
(1)判断 A 与 B 的大小关系;
(2)指出 A 与 C 哪个大?并说明理由。
4、已知 44
1
,
36
1
,
24
1
?
?
?
?
?
? ca
ac
cb
bc
ba
ab
,求 cabcab
abc
?? 的值。
5、若 m2-2m=1,求代数式 4m3-6m2-9m
m
1
? +2017 的值。
6、已知 a+b=4n+2,ab=1,若 19a2+155ab+19b2=2017,求 n 的值。
真题再现
1、已知 a-b-2=0,则 4ab-(a+b)2+7 的值= 。
2、若 a-x2=1,b-x2=2,c-x2=3,且 abc=2013.求
cbaab
c
ac
b
bc
a 111
????? 的值。
专题:判别式法解二次三项式
【知识结构】
判别式法,通过判别式解答问题,即对一元二次方程 ax2+bx+c=0(a≠0)判别式为? =b2-4ac,
当? >0 时,方程有两个不相等的实数根,当 ? =0 时,方程有两个相等的实数根;当? <0
时,方程没有实数根。判别式法在化简,构造求值,构造相关、证明题、综合应用等方面有
广泛应用。
【例题解析】
例题 1 已知关于 x 的方程 x2+2(m+1)x+m2+5=0 有两个不相等的实数根,化简:
441 2 ???? mmm
练习 若关于 x的方程(m-2)x2-2(m-1)x+m-3=0 有实数根,试讨论关于 x 的方程
(m-6)x2-2(m+1)x+m=0 的根的情况。
例题 2 已知 a,b,c 为△ABC 的三边,当 m>0 时,关于 x 的方程 c(x2+m)+b(x2-m)-2 m ax=0
有两个相等的实数根,试说明△ABC 的形状.
练习:如果一直角三角形的三边为 a, b, c,∠ B=90°,试判断关于 x 的方程
a(x2-1)-2cx+b(x2+1)=0 的根的情况。
例题 3 已知 x2-ax+3-b=0 有两个不相等的实数根,x2+(6-a)x+6-b=0 有两个相等的实数根,
x2+(4-a)x+5-b=0 无实数根,求 a,b 的取值范围;
练习:设两个方程 x2+4ax+4a2+a=0,x2+2 (a-1)x+a2=0 中至少有一个方程有实数根,求 a 的取
值范围。
例题 4 已知 x,y,z 为实数,且满足 0782 ???? xyzx 和 06622 ????? xyzzy ,求
证:1≤x≤9.
? ? 0)(
4
3)(22 ?????? caxcaxcb
练习 已知 x,y,z 为实数且满足 1??? zyx ,xy=z2-7z+14,在 z 为何值时, 22 yx ? 取
到最大值?最大值是多少?
【作业】
1. 若关于 a 的二次三项式 ka2+4a+1 是一个完全平方式,则 k 的值 ( )
A.1 B.2 C.4 D.
4
1
2.关于 x 的方程 02 ??? axx ,给出下列四个结论:
①存在实数 a,使得方程恰有 2 个不同的实根;
②存在实数 a,使得方程恰有 3 个不同的实根;
③存在实数 a,使得方程恰有 4 个不同的实根;
④存在实数 a,使得方程恰有 6 个不同的实根;
其中正确的结论个数是( )
A.1 B.2 C.3 D.4
3. 若 二 次 三 项 式 3x2-x+m 能 在 实 数 范 围 内 分 解 因 式 , 则 m 的 取 值 范 围
是: . .
4. 实数 x,y,z 满足 x+y +z=5,xy+yz+zx=3,则 z 的最大值是________.
5.已知 a,b,c为△ABC 的三边的长,方程
有两个相等的实数根,求证:△ABC 是等腰三角形。
6.若关于 x 的不等式组
?
?
?
??
??
23
2
ax
ax
有解,求函数
4
1)3( 2 ???? xxay 的图象与 x轴的交
点个数。
7.若 21 , xx 是关于 x 的方程 x2+bx+c=0 的两个实数根,且 kxx 221 ?? (k 是整数),则称方
程 x2+bx+c=0 为“偶系二次方程”,例如 x2-6x-27=0,x2-2x-8=0,x2+3x-
4
27
都是“偶系二次方程”;
(1)判断方程 x2+x-12=0 是否是“偶系二次方程”,并说明理由;
(2)对于任意一个整数 b,是否存在实数 c,使得关于 x 的方程 x2+bx+c=0 是“偶系二次方
程”,并说明理由。
8.已知实数 x,y,z 满足 x+y +z=0,xyz=2,求 zyx ?? 的最小值。
专题:不定方程
【知识结构】
不定方程(组)是指未知数的个数多于方程(组),其特点是它的解一般有多个,不能
唯一确定.
一、如何确定不定方程(组)的解?
不定方程(组)往往会给出限定条件,求的往往是不定方程(组)特殊解,如整数解、
正整数解、自然数解等等.
【例题解析】
例 1. 二元一次方程 2x+y=6 有 个解;有 个自然数解;有 个正整数解.
小结:求不定方程(组)的解,关键是看清题目要求,做到不漏不重.
练习 1.试试你的理解能力(求下例不定方程的正整数解):
(1) x+y=5; (2) 2x+3y=11; (1) 5x+2y=24; (2) 4x+3y=50.
例 2.适当提高:求方程 x+y+xy=2008 的正整数解.
小结:利用因式分解将不定方程转化为二元一次方程组求解.
练习 1.求方程 x
2
-y
2
=105 的正整数解.
练习 2.求方程(x+1)
2
+(y-2)
2
=1 的整数解有 组.
二、不定方程(组)的应用
不定方程(组)应用广泛,解决问题的关键是——充分挖掘题目隐含的条件,进而确定方
案.
例题.数学趣题:
我国古代数学家张建丘所著《算经》中的“百钱买百鸡”问题,鸡翁一,值钱五;
鸡母一,值钱三;鸡雏三,值钱一,百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?
【练习】
1. 假期到了,17 名女教师去外地培训,住宿时有 2 人间和 3 人间可供租住,若每个房间都
要住满,那么她们有几种租住方案( )
A.2 种 B.3 种 C.4 种 D.5 种
2. 地震期间为了紧急安置 60 名地震灾民,需要搭建可容纳 6 人或 4 人的帐篷,若所搭建
的帐篷恰好能容纳这 60 名灾民,则不同的搭建方案有( )
A.4 种 B.6 种 C.9 种 D.11 种
3.二中团委与社区联合举办“保护地球,人人有责”活动,选派 20 名学生分三组到 120 个
店铺发传单,若地一、二、三小组每人分别负责 8、6、5 个店铺,且每组店铺至少有两个
人,则学生分组方案有( )
A.3 种 B.4 种 C.5 种 D.6 种
4.现有球迷 150 人欲同时租用 A、B、C三种型号的客车去观看世界杯足球赛,其中 A、B、C
三种型号客车的载客量分别为 50 人、30 人、10 人,要求每辆车必须满载,其中 A型号客
车最多租两辆,则球迷们一次性达到赛场的租车方案有( )
A.3 种 B.4 种 C.5 种 D.6 种
5.小明决定买一些书包送给灾区的小朋友,超市中有 A、B、C 三种款式,其中 A 款每个 30
元,B款每个 40 元,C款每个 50 元,小明买了三款书包共 10 个,用了 400 元,问这三款
书包分别买了几个?
反思:若将题目中“小明买了三款书包共 10 个”改成“小明买了 10 个书包”,那么方案共
有哪几种?
6.某商场计划拨款 9 万元从厂家购进 50 台电视机,已知该厂生产甲、乙、丙三种不同型号
的电视机,出厂价分别为每台 1500 元、2100 元、2500 元.
(1) 某商场同时购进其中两种不同型号的电视机共 50 台,用去 9 万元,请你研究一下商
场的进货方案;
(2) 某商场销售一台甲,乙,丙型电视机分别可获利 150 元、200 元、250 元.在同时购
进两种不同型号电视机的方案中,为了使销售时获利最多,你选择哪种进货方案?
(3) 若商场准备用9万元同时购进这三种不同型号的电视机共50台,请你设计进货方案.
7.某车间共有 20 位工人,生产甲、乙、丙三种型号的零件,因受金融风暴 影响,该车间每
天只需生产甲、乙、丙三种零件共 50 件.如果丙型零件至少生产 3 件, 每人每天生产的零
件数与每个零件产值的数据如下表:
型号 每人每天生产零件数(件) 每个零件产值(元)
甲型 3 400
乙型 2 500
丙型 1 600
(1)问生产甲、乙、丙三种型号零件的工人分别有多少人?
(2)若使车间每天生产的产值最高,则生产三种型号零件的工人各有多少人?
三.解方程(组)拓展
【例题解析】
例 1.
? ?
12
1 2 5 22
4
x y z
x y z
x y
? ? ??
? ? ? ??
? ??
? ?
4 2 0
2 2 3
2 2 4
x y z
x y z
x y z
? ? ??
? ? ? ??
? ? ? ? ??
? ?
: : 1: 2 : 7
3
2 3 21
x y z
x y z
??
? ? ? ??
例 2.在实数范围内解下列方程或方程组:
【练习】解方程或方程组:
? ?
2 21 11 2 0
1
x x y
x
? ? ?
? ? ?
?
? ? 2 22 3 3 3 0x xy y x y? ? ? ? ? ?
? ? 2
2
3
2 4
x y z
xy z
? ? ??
?
? ??
? ?1 1 2 2 1 1 3 0x x y? ? ? ? ? ? ? ? 2 22 5 6 2 14 8 10 0x xy y x y? ? ? ? ? ?
? ?4 2 1 3 2 5 0x y x y? ? ? ? ? ?? ? ? ? ? ?2 23 1 4 8x y xy? ? ?
专题:含绝对值的函数
【知识结构】
1. 将含字母系数的绝对值方程转化为求函数图象的交点问题进行解决。
2. 通过数形结合思想和分类讨论思想解决字母系数的绝对值方程。
【例题解析】
例题 1 已知函数 y=∣x-2∣+1,当自变量 x 满足-1≤x≤m时,函数值 y的取值范围是 1≤y
≤4,则实数 m 的取值范围是: .
练习 : 已知函数 y=∣x-3∣-∣x+2∣,求 y 的最大值与最小值.
例题 2 设直线 y=ax+2 与函数 y=∣x-1∣-∣x-2∣+2 的图象交于三个不同的点,求实数 a的取
值范围。
练习 :方程 2x-1=a∣x-1∣有两个实数解,求实数 k 的取值范围。
例题 3 已知函数 f(x)= ∣8-2x-x2∣和一次函数 y=kx+k(k 为常数),这两个函数图象有( )
个交点。
练习 :若函数 y=b 的图象与函数 y= x2-3∣x-1∣-4x-3 的图象恰有三个交点,则 b 的可能值
为: 。
例题 4 已知函数 y=∣x2-2ax∣,其中 a 为常数
(1) 当 0≤x≤1 时,y 的最大值为 2,求 a的值;
(2) 若 a>0,当 0≤x≤2 时,y≤2,求 a 的取值范围;
(3) 当 a=-1 时,关于 x 的方程∣x2-2ax∣=m∣x-1∣有四个不同的实数解,求 m 的取值
范围。
练习:已知关于 x 的多项式 x2+bx+c,其中 b,c 是常数;
(1)当 b=2,c=-3 时,求多项式 x2+bx+c 的最小值;
(2)当 c=5 时,函数 y=x2+b∣x∣+c,若 y≥1,求 b 的取值范围;
(3)当 c=b2时,令 y=x2+bx+c,当 b≤x≤b+3 时,函数值 y 的最小值为 21,求此时二次函
数的解析式。
【作业】
1. 已知函数 y=∣x-1∣+∣x-5∣+∣x+2∣的最小值是( )
A.5 B. 6 C.7 D.8
2.已知 x 是正实数,则 y=∣x-1∣+∣2x-1∣+∣3x-1∣+∣4x-1∣+∣5x-1∣的 y最大值是
A.2 B. 3 C.4 D.5
3. 若方程∣x2-4x+3∣+ k=0 有三个根,则 k 的值是: 。
4.t 为常数,函数 y=∣x2-2x-t∣在 0≤y≤3上的最大值为 2,则 t的值: 。
5.已知如图所示,函数 )62(
3
1 2 ??? xxy 对应的曲线依次交 x轴正负半轴于点 A,B;
(1)求直线 y=
3
4
与该曲线所有交点的坐标;
(2)过点作两条互相垂直的直线分别交该曲线于点 C,D 两点,且点 C 落在 A 点右侧,D 点
落在 A,B 之间,若 AD=AC,求△ADC 的面积。
6.已知:关于 x 的方程 x 2 ? ( m ? 1) x ? m ? 2 ? 0 有两异号实数根 x1 , x2 ,且
x1> 2x ,若 x12 ? x22 ? 8 .
(1) 求 m 的值;
(2) 若函数 y ? x 2 ? bx ? c 的图像与 x 轴的两个交点的横坐标为 ? x1 ?1 ,
7. 已知关于 x 的多项式 x 2 -2|x-m|+1,其中 m 为常数.
(1)若 m=0,求方程 x
2
-2|x-m|+1=0 的根;
(2)令 y= x
2
-2|x-m|+1,当 0<m≤1 时,求 y 的最小值(用含 m 的代数式表示);
(3)若方程 x
2
-2|x-m|+1=1.5 恰有三个实数根,求 m 的值.
同课章节目录
