浙教版2018-2019学年度上学期七年级数学期末复习专题训练试卷6 第6章图形的初步认识(有答案)
文档属性
| 名称 | 浙教版2018-2019学年度上学期七年级数学期末复习专题训练试卷6 第6章图形的初步认识(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 258.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-05 09:55:32 | ||
图片预览



文档简介
浙教版2018-2019学年度(上)七年级期末复习训练试卷6
第6章图形的初步认识(有答案)
(时间:100分钟 满分:120分)
题号
1
2
3
4
5
6
7
8
9
10
答案
一、选择题(共10题 每题3分 共30分)
1、在长方形、正方体、三角形、球、射线、圆中,有( )个平面图形.
A.4????????????????????????????B.3?????????????????????????????????C.2??????????????????????????????D.1
2、A、B两点的距离是35厘米,有一点M,如果AM+BM=40厘米,那么下面结论正确的是 (??? )
A.点M一定在线段AB上??????????????????????????B.点M一定在直线AB外
C.点M一定在直线AB上??????????????????????????D.点M一定在直线AB上,也可能在直线 AB外
3、给出下列说法:①等角的补角相等;②相等的两个角一定是对顶角;③两点确定一条直线;
④若两条直线相交所形成的四个角相等,则这两条直线互相垂直. 其中正确个数是( )
A.1??????????????????????????????B.2????????????????????????????????????C.3???????????????????????????????D.4
4、若∠α与∠β互为补角,且∠α>∠β,则∠β的余角是( )
A.?????????????B.????????????????C.?????????????D.
5、如图,直线AB与直线CD相交于点O.若EO⊥AB于点O,∠1=62°,则∠2等于(?? )
A.18°???????????????????????B.28°???????????????????????????C.38°??????????????????????????D.48°
6、如图,射线和线段条数分别为( )
A.4和6 B. 5和6 C.6和7 D. 6和8
7、下列各图形中,有交点的是( )
8、下列选项中,∠1与∠2是对顶角的是( )
9、已知α、β都是钝角,则计算?的结果可能是( )
A.20° B.39.75° C.45° D.50°
10、如图,已知O是直线AB上一点,OD平分∠BOC,
若,? 则∠2的度数是(? ?????)
A、65° B、70°?????????? ???
C、75° D、80°
二、填空题(共10题 每题3分 共30分)
11、 °.
12、往返A、B两地的火车,中途还需停靠5个站,则铁路部门对此运行区间应准备________ 种不同的火车票.
13、点 A、B在直线l两侧,点P是直线l上的动点,则使PA+PB值最小的点P的位置是________?.
14、如图,从A到B要经过点C,人们通常会走连接AB的斜的直路,而不愿意走从A到C再到B这条路,这其中的道理是________?.
?
.
15、一个锐角的补角与这个角的余角的差的度数是 .
16、如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则∠AOC+∠DOB的度数是________.
17、钟面上3点40分时,时针与分针的夹角的度数是________度.
18、线段AB的长为14,点C为线段AB的中点,点D在直线AB上,且DB=6,则线段CD的长为________?.
19、如图,O是直线AB上的一点,DO⊥AB,CO⊥EO.
(1)如果∠1=68°,那么∠3= ,∠4= ;
(2)和∠1互为余角的有 ,和∠1相等的角有 ;
(3)OE的方向是 ,OC的方向是 .
20、在平面内有若干条直线,在下列情形下,可将平面最多分成几部分?
(1)有一条直线时,最多分成2 部分;(2)有两条直线时,最多分成 部分;
(3)有三条直线时,最多分成 部分;(4)有n条直线时,最多分成 部分.
三、解答题(共6题 共60分)
21、(8分)如图,在平面内有A、B、C、D四点.
(1)画直线AC和DC,线段AB,射线DB;
(2)在线段AB上任取一点E(不同于A、B),连接线段DE,交AC于点F.
22、(10分)一个角的余角比它的补角的大12°,求这个角的度数.
23、(10分)已知线段a、b,画线段c=3a2b .
24、(10分)如图,已知直线AB与直线ED相交于点O,射线OA平分∠COE, OM,ON分别为∠BOC,∠BOD的平分线.
(1)∠BOD与∠BOC相补吗?请说明理由;
(2)若∠MON=46°,试求∠AOC与∠COD的度数.
25、(10分)如图,线段AC=14cm,点M在线段AC上,且AM:MC=4:3,若点N为线段CB的中点,,求AB的长.
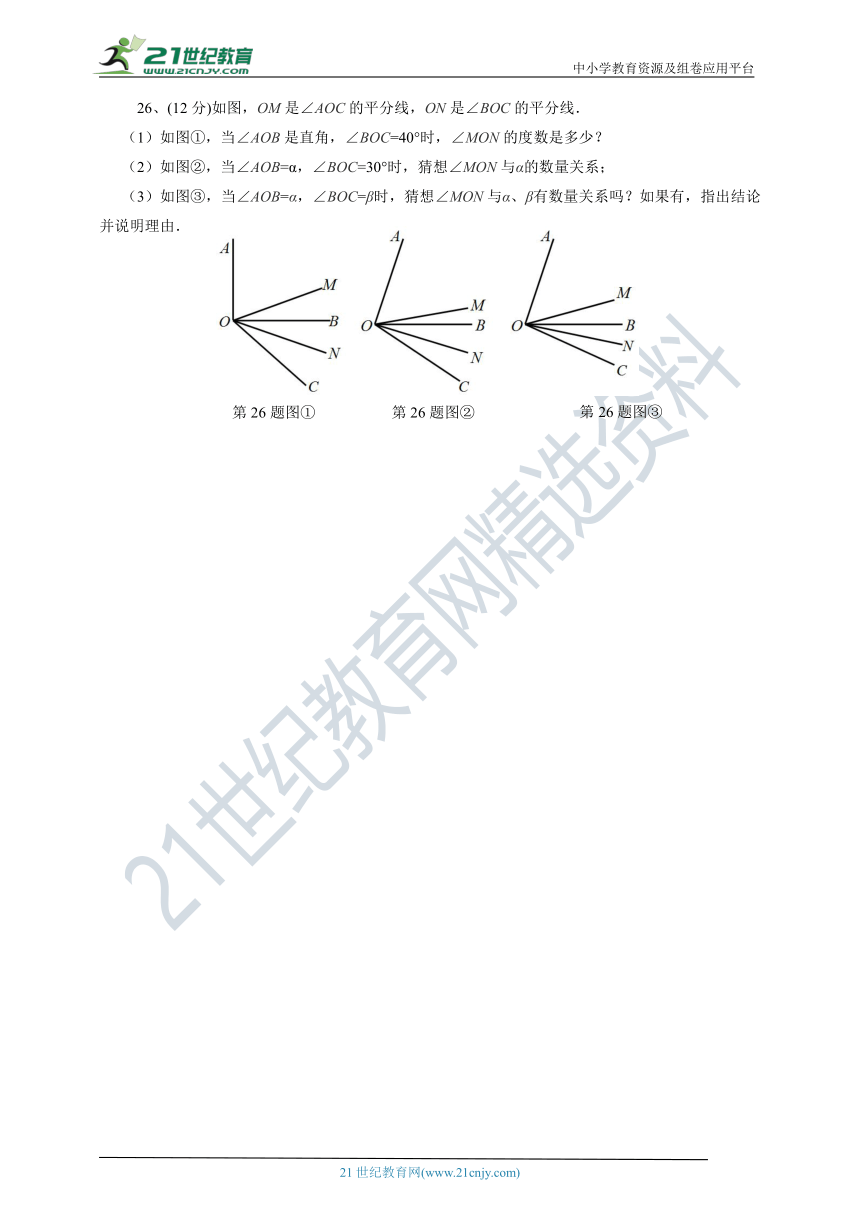
26、(12分)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图①,当∠AOB是直角,∠BOC=40°时,∠MON的度数是多少?
(2)如图②,当∠AOB=α,∠BOC=30°时,猜想∠MON与α的数量关系;
(3)如图③,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
参考答案
一、选择题(共10小题 每题3分 共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
A
B
D
B
C
B
C
二、填空题(共8小题 每题3分 共24分)
11、88.6 12、56 13、连接AB与直线l的交点, 14、两点之间线段最短 15、90°
16、180° 17、130° 18、13或1 19、(1)68°,22° (2)∠2,∠4,∠3(3)北偏东68°,北偏西22° 20、(2)4 (3)7 (4)
三、解答题(共6题 共60分)
21、(12分)如图,在平面内有A、B、C、D四点.
(1)画直线AC和DC,线段AB,射线DB;
(2)在线段AB上任取一点E(不同于A、B),连接线段DE,交AC于点F.
解:如图所示
22、(8分)一个角的余角比它的补角的大12°,求这个角的度数.
解:设这个角为x度,
则这个角的余角是(90x)度,补角是(180x)度.
根据题意,得,
解方程,得.
所以这个角的度数为27°.
23、(10分)已知线段a、b,画线段c=3a2b .
作法:(1)画射线AM,
(2)在射线AM上截取AB=3a,
(3)在线段AB上截取线段BD=2b,
所以线段AD就是要画的线段c.
24、(8分)如图,已知直线AB与直线ED相交于点O,射线OA平分∠COE, OM,ON分别为∠BOC,∠BOD的平分线.
(1)∠BOD与∠BOC相补吗?请说明理由;
(2)若∠MON=46°,试求∠AOC与∠COD的度数.
解:(1)互补,理由如下:
∵射线OA平分∠COE,
∴∠AOE=∠AOC.
∵∠AOE与∠BOD是对顶角,
∴∠AOE=∠BOD.
∴∠AOC=∠BOD.
∵∠AOC+∠COB=180°,
∴∠BOD +∠COB=180°.
∴∠BOD与∠BOC相补.
(2)设∠BON为x度,
∵ON平分∠BOD,
∴∠BON=∠DON=x,∴∠BOD=2x.
∵∠BOD +∠COB=180°,
∴∠COB=180°∠BOD=180°2x.
∵OM平分∠BOC,
∴∠MOB=∠MOC=(180°2x)°÷2=(90x)°.
∴∠MON=∠MOB∠NOB.
即90xx=46.解得x=22.
∴∠BOD=2×22°=44°.
∴∠AOC=∠BOD=44°.
∴
.
25、(10分)如图,线段AC=14cm,点M在线段AC上,且AM:MC=4:3,若点N为线段CB的中点,,求AB的长.
解:∵AC=14cm ,AM:MC=4:3,
∴.
∵点N为线段CB的中点,
∴CN=BN.
设BN的长为x,则CN的长为x,
∴,
∴,
解得x=9.
∴CB=2NB=2×9=18,
∴AB=AC+CB=14+18=32.
26、(12分)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图①,当∠AOB是直角,∠BOC=40°时,∠MON的度数是多少?
(2)如图②,当∠AOB=α,∠BOC=30°时,猜想∠MON与α的数量关系;
(3)如图③,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
解:(1)如图1,∵∠AOB=90°,∠BOC=40°,
∴∠AOC=90°+40°=130°,
∵OM平分∠AOC,ON平分∠BOC,
∴, .
∴∠MON=∠MOC∠NOC=45°.???
(2)如图2,,理由如下:
∵∠AOB=α,∠BOC=30°,
∴∠AOC=α+30°,
∵OM平分∠AOC,ON平分∠BOC,
∴,.
∴.
(3)如图3,,与β的大小无关.???
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.?????????
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴,
,
∴
即.
第6章图形的初步认识(有答案)
(时间:100分钟 满分:120分)
题号
1
2
3
4
5
6
7
8
9
10
答案
一、选择题(共10题 每题3分 共30分)
1、在长方形、正方体、三角形、球、射线、圆中,有( )个平面图形.
A.4????????????????????????????B.3?????????????????????????????????C.2??????????????????????????????D.1
2、A、B两点的距离是35厘米,有一点M,如果AM+BM=40厘米,那么下面结论正确的是 (??? )
A.点M一定在线段AB上??????????????????????????B.点M一定在直线AB外
C.点M一定在直线AB上??????????????????????????D.点M一定在直线AB上,也可能在直线 AB外
3、给出下列说法:①等角的补角相等;②相等的两个角一定是对顶角;③两点确定一条直线;
④若两条直线相交所形成的四个角相等,则这两条直线互相垂直. 其中正确个数是( )
A.1??????????????????????????????B.2????????????????????????????????????C.3???????????????????????????????D.4
4、若∠α与∠β互为补角,且∠α>∠β,则∠β的余角是( )
A.?????????????B.????????????????C.?????????????D.
5、如图,直线AB与直线CD相交于点O.若EO⊥AB于点O,∠1=62°,则∠2等于(?? )
A.18°???????????????????????B.28°???????????????????????????C.38°??????????????????????????D.48°
6、如图,射线和线段条数分别为( )
A.4和6 B. 5和6 C.6和7 D. 6和8
7、下列各图形中,有交点的是( )
8、下列选项中,∠1与∠2是对顶角的是( )
9、已知α、β都是钝角,则计算?的结果可能是( )
A.20° B.39.75° C.45° D.50°
10、如图,已知O是直线AB上一点,OD平分∠BOC,
若,? 则∠2的度数是(? ?????)
A、65° B、70°?????????? ???
C、75° D、80°
二、填空题(共10题 每题3分 共30分)
11、 °.
12、往返A、B两地的火车,中途还需停靠5个站,则铁路部门对此运行区间应准备________ 种不同的火车票.
13、点 A、B在直线l两侧,点P是直线l上的动点,则使PA+PB值最小的点P的位置是________?.
14、如图,从A到B要经过点C,人们通常会走连接AB的斜的直路,而不愿意走从A到C再到B这条路,这其中的道理是________?.
?
.
15、一个锐角的补角与这个角的余角的差的度数是 .
16、如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则∠AOC+∠DOB的度数是________.
17、钟面上3点40分时,时针与分针的夹角的度数是________度.
18、线段AB的长为14,点C为线段AB的中点,点D在直线AB上,且DB=6,则线段CD的长为________?.
19、如图,O是直线AB上的一点,DO⊥AB,CO⊥EO.
(1)如果∠1=68°,那么∠3= ,∠4= ;
(2)和∠1互为余角的有 ,和∠1相等的角有 ;
(3)OE的方向是 ,OC的方向是 .
20、在平面内有若干条直线,在下列情形下,可将平面最多分成几部分?
(1)有一条直线时,最多分成2 部分;(2)有两条直线时,最多分成 部分;
(3)有三条直线时,最多分成 部分;(4)有n条直线时,最多分成 部分.
三、解答题(共6题 共60分)
21、(8分)如图,在平面内有A、B、C、D四点.
(1)画直线AC和DC,线段AB,射线DB;
(2)在线段AB上任取一点E(不同于A、B),连接线段DE,交AC于点F.
22、(10分)一个角的余角比它的补角的大12°,求这个角的度数.
23、(10分)已知线段a、b,画线段c=3a2b .
24、(10分)如图,已知直线AB与直线ED相交于点O,射线OA平分∠COE, OM,ON分别为∠BOC,∠BOD的平分线.
(1)∠BOD与∠BOC相补吗?请说明理由;
(2)若∠MON=46°,试求∠AOC与∠COD的度数.
25、(10分)如图,线段AC=14cm,点M在线段AC上,且AM:MC=4:3,若点N为线段CB的中点,,求AB的长.
26、(12分)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图①,当∠AOB是直角,∠BOC=40°时,∠MON的度数是多少?
(2)如图②,当∠AOB=α,∠BOC=30°时,猜想∠MON与α的数量关系;
(3)如图③,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
参考答案
一、选择题(共10小题 每题3分 共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
A
B
D
B
C
B
C
二、填空题(共8小题 每题3分 共24分)
11、88.6 12、56 13、连接AB与直线l的交点, 14、两点之间线段最短 15、90°
16、180° 17、130° 18、13或1 19、(1)68°,22° (2)∠2,∠4,∠3(3)北偏东68°,北偏西22° 20、(2)4 (3)7 (4)
三、解答题(共6题 共60分)
21、(12分)如图,在平面内有A、B、C、D四点.
(1)画直线AC和DC,线段AB,射线DB;
(2)在线段AB上任取一点E(不同于A、B),连接线段DE,交AC于点F.
解:如图所示
22、(8分)一个角的余角比它的补角的大12°,求这个角的度数.
解:设这个角为x度,
则这个角的余角是(90x)度,补角是(180x)度.
根据题意,得,
解方程,得.
所以这个角的度数为27°.
23、(10分)已知线段a、b,画线段c=3a2b .
作法:(1)画射线AM,
(2)在射线AM上截取AB=3a,
(3)在线段AB上截取线段BD=2b,
所以线段AD就是要画的线段c.
24、(8分)如图,已知直线AB与直线ED相交于点O,射线OA平分∠COE, OM,ON分别为∠BOC,∠BOD的平分线.
(1)∠BOD与∠BOC相补吗?请说明理由;
(2)若∠MON=46°,试求∠AOC与∠COD的度数.
解:(1)互补,理由如下:
∵射线OA平分∠COE,
∴∠AOE=∠AOC.
∵∠AOE与∠BOD是对顶角,
∴∠AOE=∠BOD.
∴∠AOC=∠BOD.
∵∠AOC+∠COB=180°,
∴∠BOD +∠COB=180°.
∴∠BOD与∠BOC相补.
(2)设∠BON为x度,
∵ON平分∠BOD,
∴∠BON=∠DON=x,∴∠BOD=2x.
∵∠BOD +∠COB=180°,
∴∠COB=180°∠BOD=180°2x.
∵OM平分∠BOC,
∴∠MOB=∠MOC=(180°2x)°÷2=(90x)°.
∴∠MON=∠MOB∠NOB.
即90xx=46.解得x=22.
∴∠BOD=2×22°=44°.
∴∠AOC=∠BOD=44°.
∴
.
25、(10分)如图,线段AC=14cm,点M在线段AC上,且AM:MC=4:3,若点N为线段CB的中点,,求AB的长.
解:∵AC=14cm ,AM:MC=4:3,
∴.
∵点N为线段CB的中点,
∴CN=BN.
设BN的长为x,则CN的长为x,
∴,
∴,
解得x=9.
∴CB=2NB=2×9=18,
∴AB=AC+CB=14+18=32.
26、(12分)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图①,当∠AOB是直角,∠BOC=40°时,∠MON的度数是多少?
(2)如图②,当∠AOB=α,∠BOC=30°时,猜想∠MON与α的数量关系;
(3)如图③,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
解:(1)如图1,∵∠AOB=90°,∠BOC=40°,
∴∠AOC=90°+40°=130°,
∵OM平分∠AOC,ON平分∠BOC,
∴, .
∴∠MON=∠MOC∠NOC=45°.???
(2)如图2,,理由如下:
∵∠AOB=α,∠BOC=30°,
∴∠AOC=α+30°,
∵OM平分∠AOC,ON平分∠BOC,
∴,.
∴.
(3)如图3,,与β的大小无关.???
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.?????????
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴,
,
∴
即.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
