浙教版九年级下《第二章直线与圆的位置关系》单元评估试题有答案
文档属性
| 名称 | 浙教版九年级下《第二章直线与圆的位置关系》单元评估试题有答案 |  | |
| 格式 | zip | ||
| 文件大小 | 207.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-05 19:00:28 | ||
图片预览



文档简介
浙教版九年级数学下册 第二章 直线与圆的位置关系 单元评估检测试题
一、单选题(共10题;共30分)
1.如图,直线l是⊙O的切线,点A为切点,B为直线l上一点,连接OB交⊙O于点C,D是优弧AC上一点,连接AD,CD.若∠ABO=40°.则∠D的大小是( ??) /
A.?50°???????????????????????????????????????B.?40°???????????????????????????????????????C.?35°???????????????????????????????????????D.?25°
2.已知直角三角形的两条直角边分别为12cm和16cm,则这个直角三角形内切圆的半径是( ??)
A.?2cm?????????????????????????????????????B.?3cm?????????????????????????????????????C.?4cm?????????????????????????????????????D.?5cm
3.如图,已知△ABC中,AB= AC,∠ABC=70°,点I是△ABC的内心,则∠BIC的度数为(????? ) /
A.?40°?????????????????????????????????????/B.?70°?????????????????????????????????????/C.?110°?????????????????????????????????????/D.?140°
4.如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( ) /
A.?
4
5
??????????????????????????????????????????B.?
3
5
??????????????????????????????????????????C.?
4
3
??????????????????????????????????????????D.?
3
4
5.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
????
∧
上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( ) /
A.?12???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?4
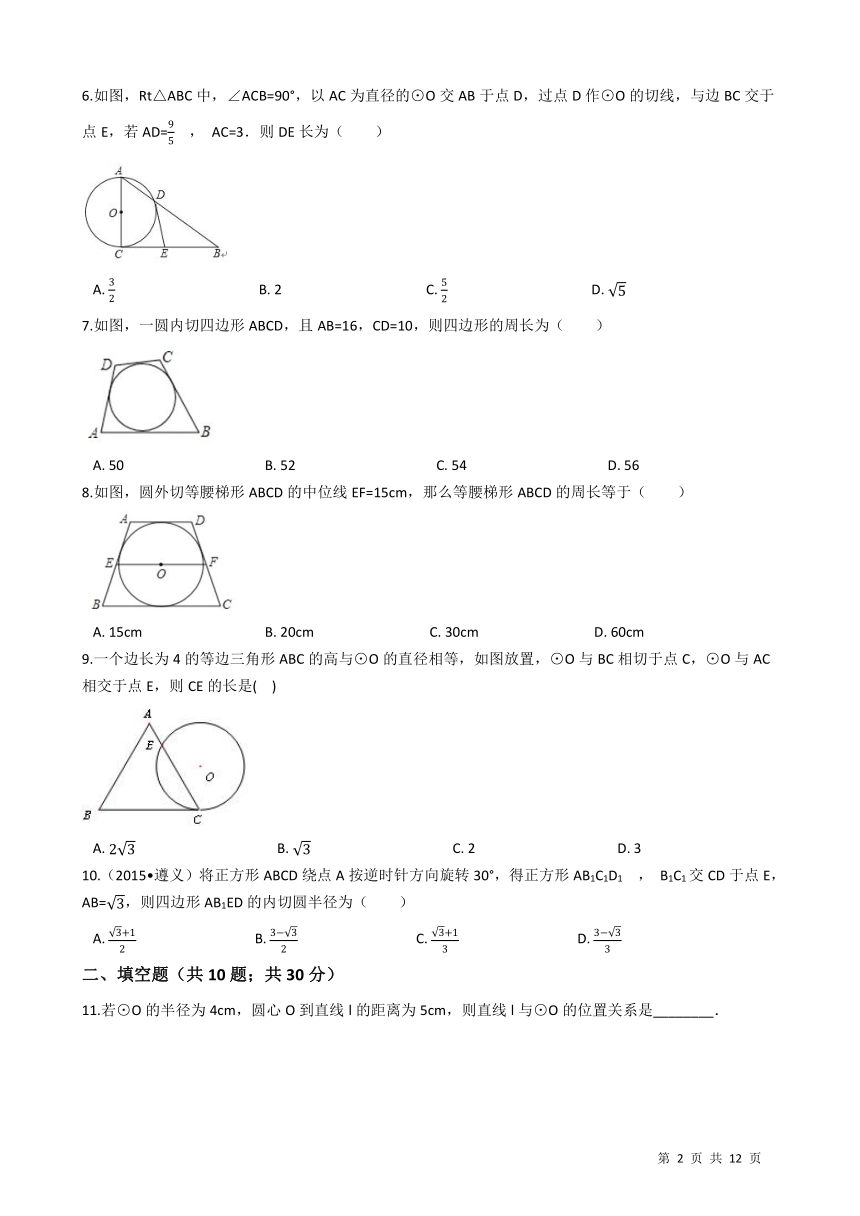
6.如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=
9
5
, AC=3.则DE长为( ) /
A.?
3
2
??????????????????????????????????????????B.?2??????????????????????????????????????????C.?
5
2
??????????????????????????????????????????D.?
5
7.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( ) /
A.?50?????????????????????????????????????????B.?52?????????????????????????????????????????C.?54?????????????????????????????????????????D.?56
8.如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于( ) /
A.?15cm???????????????????????????????????/B.?20cm?????????????????????????????????/C.?30cm?????????????????????????????????/D.?60cm
9.一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是(?? ) /
A.?2
3
?????????????????????????????????????????/B.?
3
?????????????????????????????????????????/C.?2?????????????????????????????????????????/D.?3
10.(2015?遵义)将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1 , B1C1交CD于点E,AB=
3
,则四边形AB1ED的内切圆半径为( )
A.?
3
+1
2
??????????????????????????????????/B.?
3?
3
2
??????????????????????????????????/C.?
3
+1
3
??????????????????????????????????/D.?
3?
3
3
二、填空题(共10题;共30分)
11.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是________.
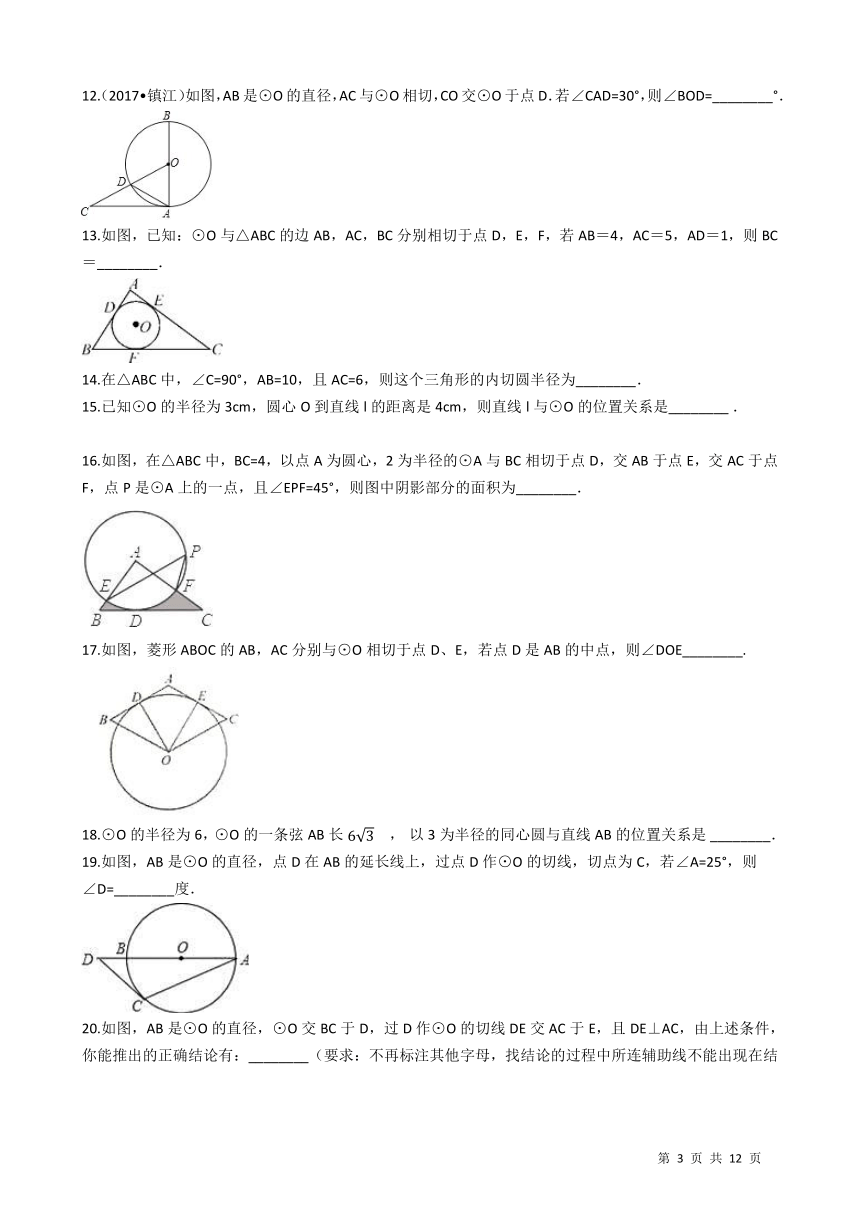
12.(2017?镇江)如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°. /
13.如图,已知:⊙O与△ABC的边AB,AC,BC分别相切于点D,E,F,若AB=4,AC=5,AD=1,则BC=________.
/
14.在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为________.
15.已知⊙O的半径为3cm,圆心O到直线l的距离是4cm,则直线l与⊙O的位置关系是________?.
16.如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为________.
/
17.如图,菱形ABOC的AB,AC分别与⊙O相切于点D、E,若点D是AB的中点,则∠DOE________. /
18.⊙O的半径为6,⊙O的一条弦AB长6
3
, 以3为半径的同心圆与直线AB的位置关系是?________.
19.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=________度.
/
20.如图,AB是⊙O的直径,⊙O交BC于D,过D作⊙O的切线DE交AC于E,且DE⊥AC,由上述条件,你能推出的正确结论有:________(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,至少写出4个结论,结论不能类同). /
三、解答题(共8题;共60分)
21.如图,点I是△ABC的内心,∠A=80°,求∠BIC的度数./
22.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线. /
23.已知:如图,在 △?????? 中, ????=???? ,以 ???? 为直径的 ⊙?? 交 ???? 于点 ?? ,过点 ?? 作 ????⊥???? 于点 ?? .求证: ???? 是 ⊙?? 的切线.
/
24.如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E. (1)求证:BD=ID; (2)求证:ID2=DE?DA. /
25.如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E. (1)求证:直线CD为⊙O的切线; (2)当AB=2BE,且CE=时,求AD的长. /
26.如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D,交BC于点E,连接BD. (1)线段BD与ID相等吗?证明你的结论. (2)证明:ID2=DE?AD. /
27.如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD= 50°,求证:CD是⊙O的切线. ?/
28.已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E. (1)如图,求证:EB=EC=ED; (2)试问在线段DC上是否存在点F,满足BC2=4DF?DC?若存在,作出点F,并予以证明;若不存在,请说明理由. /
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
二、填空题
11.【答案】相离
12.【答案】120
13.【答案】7
14.【答案】2
15.【答案】相离
16.【答案】4-π
17.【答案】60°
18.【答案】相切
19.【答案】40
20.【答案】∠ADB=∠AED=∠CED=90°, △ADE∽△ABD,∠ADE=∠B,∠CAD=∠BAD
三、解答题
21.【答案】解:∵点I是△ABC的内心,∴∠IBC=
1
2
∠ABC,∠ICB=
1
2
∠ACB ,∴∠IBC+∠ICB=
1
2
(∠ABC+∠ACB). ∵∠A=80°,∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,∴∠IBC+∠ICB=
1
2
×100°=50°, ∴∠BIC=180°-(∠IBC+∠ICB)=180°-50°=130°
22.【答案】证明:连接OD; ∵AD平行于OC, ∴∠COD=∠ODA,∠COB=∠A; ∵∠ODA=∠A, ∴∠COD=∠COB,OC=OC,OD=OB, ∴△OCD≌△OCB, ∴∠CDO=∠CBO=90°. ∴DC是⊙O的切线.
23.【答案】解:连接OD.
/
∵OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠ODE=∠DEC;
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线.
24.【答案】(2)证明:连接BI,CI,CD, ∵I为内心, ∴AI为∠BAC角平分线, BI为∠ABC平分线, ∴∠ABI=∠CBI,∠BAD=∠DAC, ∵∠BID=∠ABI+∠BAI, ∠CBD=∠DAC=∠BAI, ∴∠BID=∠CBI+∠CBD=∠DBI, ∴△DBI为等腰三角形, ∴DB=DI; (3)证明:∵∠DBE=∠CAD,∠BAE=∠CAE, ∴∠BAE=∠EBD, ∴△DBE∽△DAB, ∴
????
????
=
????
????
, ∴DB2=DE?DA, 又∵DB=DI(已证), ∴DI2=DE?DA. /
25.【答案】(1)证明:连接OC, ∵AC平分∠DAB, ∴∠1=∠2, ∵又AO=CO, ∴∠3=∠2, ∴∠1=∠3, ∴OC∥AD, ∵又CD⊥AD, ∴CD⊥OC, ∴CD为⊙O的切线; / (2)解:∵直径AB=2BE, ∴OE=2OC, 在Rt△EOC中,设CO=x,即OE=2x, 由勾股定理得:CE=
3
x, 又∵CE=
3
, ∴x=1 即OC=1, ∵OC∥AD(已证)? ∴△EOC∽△EAD, ∴
????
????
=
????
????
, 即
1
????
=
2
3
,? ∴AD=
3
2
26.【答案】解:(1)ID=BD, 理由:∵I是△ABC的内心, ∴∠1=∠2,∠3=∠4; ∵∠BID=∠3+∠2,∠DBI=∠4+∠5,且∠5=∠1, ∴∠BID=∠DBI; ∴ID=BD; (2)证明:如图所示: ∵∠5=∠1,∠1=∠2; ∴∠5=∠2; 又∵∠D=∠D, ∴△BDE∽△ADB; ∴BD:DE=AD:BD; ∴BD2=AD?DE; 又∵ID=BD, ∴ID2=AD?DE. /
27.【答案】证明:连接DO, ∵AO=DO, ∴∠DAO=∠ADO=20°, ∴∠COD=∠A+∠ADO=40°, ∵∠ACD=50°, ∴∠ODC=90°. ∴CD是⊙O的切线. ?/
28.【答案】(1)证明:连接BD. 由于ED、EB是⊙O的切线,由切线长定理,得 ED=EB,∠DEO=∠BEO, ∴OE垂直平分BD. 又∵AB是⊙O的直径, ∴AD⊥BD. ∴AD∥OE. 即OE∥AC. 又O为AB的中点, ∴OE为△ABC的中位线, ∴BE=EC, ∴EB=EC=ED. (2)解:在△DEC中,由于ED=EC, ∴∠C=∠CDE, ∴∠DEC=180°﹣2∠C. ①当∠DEC>∠C时,有180°﹣2∠C>∠C,即0°<∠C<60°时,在线段DC上存在点F 满足条件. 在∠DEC内,以ED为一边,作∠DEF,使∠DEF=∠C,且EF交DC于点F,则点F即为所求. 这是因为: 在△DCE和△DEF中, ∠CDE=∠EDF,∠C=∠DEF, ∴△DEF∽△DCE. ∴DE2=DF?DC. 即(
1
2
BC)2=DF?DC ∴BC2=4DF?DC. ②当∠DEC=∠C时,△DEC为等边三角形,即∠DEC=∠C=60°, 此时,C点即为满足条件的F点,于是,DF=DC=DE,仍有BC2=4DE2=4DF?DC. ③当∠DEC<∠C时,即180°﹣2∠C<∠C,60°<∠C<90°;所作的∠DEF>∠DEC,此时点 F在DC的延长线上,故线段DC上不存在满足条件的点F. /
一、单选题(共10题;共30分)
1.如图,直线l是⊙O的切线,点A为切点,B为直线l上一点,连接OB交⊙O于点C,D是优弧AC上一点,连接AD,CD.若∠ABO=40°.则∠D的大小是( ??) /
A.?50°???????????????????????????????????????B.?40°???????????????????????????????????????C.?35°???????????????????????????????????????D.?25°
2.已知直角三角形的两条直角边分别为12cm和16cm,则这个直角三角形内切圆的半径是( ??)
A.?2cm?????????????????????????????????????B.?3cm?????????????????????????????????????C.?4cm?????????????????????????????????????D.?5cm
3.如图,已知△ABC中,AB= AC,∠ABC=70°,点I是△ABC的内心,则∠BIC的度数为(????? ) /
A.?40°?????????????????????????????????????/B.?70°?????????????????????????????????????/C.?110°?????????????????????????????????????/D.?140°
4.如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( ) /
A.?
4
5
??????????????????????????????????????????B.?
3
5
??????????????????????????????????????????C.?
4
3
??????????????????????????????????????????D.?
3
4
5.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
????
∧
上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( ) /
A.?12???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?4
6.如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=
9
5
, AC=3.则DE长为( ) /
A.?
3
2
??????????????????????????????????????????B.?2??????????????????????????????????????????C.?
5
2
??????????????????????????????????????????D.?
5
7.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( ) /
A.?50?????????????????????????????????????????B.?52?????????????????????????????????????????C.?54?????????????????????????????????????????D.?56
8.如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于( ) /
A.?15cm???????????????????????????????????/B.?20cm?????????????????????????????????/C.?30cm?????????????????????????????????/D.?60cm
9.一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是(?? ) /
A.?2
3
?????????????????????????????????????????/B.?
3
?????????????????????????????????????????/C.?2?????????????????????????????????????????/D.?3
10.(2015?遵义)将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1 , B1C1交CD于点E,AB=
3
,则四边形AB1ED的内切圆半径为( )
A.?
3
+1
2
??????????????????????????????????/B.?
3?
3
2
??????????????????????????????????/C.?
3
+1
3
??????????????????????????????????/D.?
3?
3
3
二、填空题(共10题;共30分)
11.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是________.
12.(2017?镇江)如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°. /
13.如图,已知:⊙O与△ABC的边AB,AC,BC分别相切于点D,E,F,若AB=4,AC=5,AD=1,则BC=________.
/
14.在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为________.
15.已知⊙O的半径为3cm,圆心O到直线l的距离是4cm,则直线l与⊙O的位置关系是________?.
16.如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为________.
/
17.如图,菱形ABOC的AB,AC分别与⊙O相切于点D、E,若点D是AB的中点,则∠DOE________. /
18.⊙O的半径为6,⊙O的一条弦AB长6
3
, 以3为半径的同心圆与直线AB的位置关系是?________.
19.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=________度.
/
20.如图,AB是⊙O的直径,⊙O交BC于D,过D作⊙O的切线DE交AC于E,且DE⊥AC,由上述条件,你能推出的正确结论有:________(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,至少写出4个结论,结论不能类同). /
三、解答题(共8题;共60分)
21.如图,点I是△ABC的内心,∠A=80°,求∠BIC的度数./
22.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线. /
23.已知:如图,在 △?????? 中, ????=???? ,以 ???? 为直径的 ⊙?? 交 ???? 于点 ?? ,过点 ?? 作 ????⊥???? 于点 ?? .求证: ???? 是 ⊙?? 的切线.
/
24.如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E. (1)求证:BD=ID; (2)求证:ID2=DE?DA. /
25.如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E. (1)求证:直线CD为⊙O的切线; (2)当AB=2BE,且CE=时,求AD的长. /
26.如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D,交BC于点E,连接BD. (1)线段BD与ID相等吗?证明你的结论. (2)证明:ID2=DE?AD. /
27.如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD= 50°,求证:CD是⊙O的切线. ?/
28.已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E. (1)如图,求证:EB=EC=ED; (2)试问在线段DC上是否存在点F,满足BC2=4DF?DC?若存在,作出点F,并予以证明;若不存在,请说明理由. /
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
二、填空题
11.【答案】相离
12.【答案】120
13.【答案】7
14.【答案】2
15.【答案】相离
16.【答案】4-π
17.【答案】60°
18.【答案】相切
19.【答案】40
20.【答案】∠ADB=∠AED=∠CED=90°, △ADE∽△ABD,∠ADE=∠B,∠CAD=∠BAD
三、解答题
21.【答案】解:∵点I是△ABC的内心,∴∠IBC=
1
2
∠ABC,∠ICB=
1
2
∠ACB ,∴∠IBC+∠ICB=
1
2
(∠ABC+∠ACB). ∵∠A=80°,∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,∴∠IBC+∠ICB=
1
2
×100°=50°, ∴∠BIC=180°-(∠IBC+∠ICB)=180°-50°=130°
22.【答案】证明:连接OD; ∵AD平行于OC, ∴∠COD=∠ODA,∠COB=∠A; ∵∠ODA=∠A, ∴∠COD=∠COB,OC=OC,OD=OB, ∴△OCD≌△OCB, ∴∠CDO=∠CBO=90°. ∴DC是⊙O的切线.
23.【答案】解:连接OD.
/
∵OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠ODE=∠DEC;
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线.
24.【答案】(2)证明:连接BI,CI,CD, ∵I为内心, ∴AI为∠BAC角平分线, BI为∠ABC平分线, ∴∠ABI=∠CBI,∠BAD=∠DAC, ∵∠BID=∠ABI+∠BAI, ∠CBD=∠DAC=∠BAI, ∴∠BID=∠CBI+∠CBD=∠DBI, ∴△DBI为等腰三角形, ∴DB=DI; (3)证明:∵∠DBE=∠CAD,∠BAE=∠CAE, ∴∠BAE=∠EBD, ∴△DBE∽△DAB, ∴
????
????
=
????
????
, ∴DB2=DE?DA, 又∵DB=DI(已证), ∴DI2=DE?DA. /
25.【答案】(1)证明:连接OC, ∵AC平分∠DAB, ∴∠1=∠2, ∵又AO=CO, ∴∠3=∠2, ∴∠1=∠3, ∴OC∥AD, ∵又CD⊥AD, ∴CD⊥OC, ∴CD为⊙O的切线; / (2)解:∵直径AB=2BE, ∴OE=2OC, 在Rt△EOC中,设CO=x,即OE=2x, 由勾股定理得:CE=
3
x, 又∵CE=
3
, ∴x=1 即OC=1, ∵OC∥AD(已证)? ∴△EOC∽△EAD, ∴
????
????
=
????
????
, 即
1
????
=
2
3
,? ∴AD=
3
2
26.【答案】解:(1)ID=BD, 理由:∵I是△ABC的内心, ∴∠1=∠2,∠3=∠4; ∵∠BID=∠3+∠2,∠DBI=∠4+∠5,且∠5=∠1, ∴∠BID=∠DBI; ∴ID=BD; (2)证明:如图所示: ∵∠5=∠1,∠1=∠2; ∴∠5=∠2; 又∵∠D=∠D, ∴△BDE∽△ADB; ∴BD:DE=AD:BD; ∴BD2=AD?DE; 又∵ID=BD, ∴ID2=AD?DE. /
27.【答案】证明:连接DO, ∵AO=DO, ∴∠DAO=∠ADO=20°, ∴∠COD=∠A+∠ADO=40°, ∵∠ACD=50°, ∴∠ODC=90°. ∴CD是⊙O的切线. ?/
28.【答案】(1)证明:连接BD. 由于ED、EB是⊙O的切线,由切线长定理,得 ED=EB,∠DEO=∠BEO, ∴OE垂直平分BD. 又∵AB是⊙O的直径, ∴AD⊥BD. ∴AD∥OE. 即OE∥AC. 又O为AB的中点, ∴OE为△ABC的中位线, ∴BE=EC, ∴EB=EC=ED. (2)解:在△DEC中,由于ED=EC, ∴∠C=∠CDE, ∴∠DEC=180°﹣2∠C. ①当∠DEC>∠C时,有180°﹣2∠C>∠C,即0°<∠C<60°时,在线段DC上存在点F 满足条件. 在∠DEC内,以ED为一边,作∠DEF,使∠DEF=∠C,且EF交DC于点F,则点F即为所求. 这是因为: 在△DCE和△DEF中, ∠CDE=∠EDF,∠C=∠DEF, ∴△DEF∽△DCE. ∴DE2=DF?DC. 即(
1
2
BC)2=DF?DC ∴BC2=4DF?DC. ②当∠DEC=∠C时,△DEC为等边三角形,即∠DEC=∠C=60°, 此时,C点即为满足条件的F点,于是,DF=DC=DE,仍有BC2=4DE2=4DF?DC. ③当∠DEC<∠C时,即180°﹣2∠C<∠C,60°<∠C<90°;所作的∠DEF>∠DEC,此时点 F在DC的延长线上,故线段DC上不存在满足条件的点F. /
