1.2.2 二次根式的性质(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 1.2.2 二次根式的性质(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 329.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-02 14:26:20 | ||
图片预览



文档简介
浙江版八年级数学下册第1章二次根式1.2二次根式的性质
第2课时 二次根式的性质(2)
【知识清单】
一、二次根式的性质:?
1. (a≥0,b≥0)
2. (a≥0,b>0)
二、最简二次根式
像、、这样,(1)被开方数不含分母;(2) 被开方数中不含开得尽方的因数或因式,这样的二次根式称为最简二次根式.
在二次根式的运算中,一般要把最后结果化为最简二次根式或有理式.
【经典例题】
例题1、化简下列各式:
(1)= ;(2)= ; (3)= .
【考点】二次根式的性质.?
【分析】利用二次根式的性质进行化简即可.
【解答】(1)= ;
(2)= ;
(3)= .
【点评】本题考查了二次根式的性质:在二次根式的运算中,一般要把最后结果化为最简二次根式或有理式.
例题2、在△ABC中,已知AB=,AC=4,BC=,则△ABC的面积为( )
A. B. C.6 D.
【考点】二次根式的简单应用.
【分析】根据题意可得出BC2=AB2+AC2,再由勾股定理的逆定理可得出△ABC为Rt△,从而得出△ABC的面积.
【解答】∵AB=,AC=4,BC=,
∴AB2=7,AC2=16,BC2=23,
∴BC2=AB2+AC2,
∴△ABC为直角三角形,
∴S△ABC=.
故答案为:选A.
【点评】本题考查了勾股定理的逆定理,已知三角形的三边满足a2+b2=c2,从而得出三角形为直角三角形.
【夯实基础】
1.计算的结果是( )
A. B. ± C. D. ±
2. 若有意义,则不等式axb>0的解集是
A. B. C. D.
3.化简的结果是( )
A. B. C. D.
4. 成立的条件是( )
A. x≥3 B. x≤3 C. 3≤x≤3 D. x=3
5. 把下列根式化成最简二次根式
(1)= ; (2)= .
6. = .
7.先化简,再求出下面算式的近似值:
(1) (精确到千分位); (2) (精确到0.01)
8.化简
(1) (2) (a≥0, b≥0) (3) (4)
【提优特训】
9.化简:①;②;③;
④;⑤,其中正确的是( )个
A. 1 B. 2 C. 3 D. 4
10.若,则用含有x的代数式表示为( )
A. 10x B. C. D.
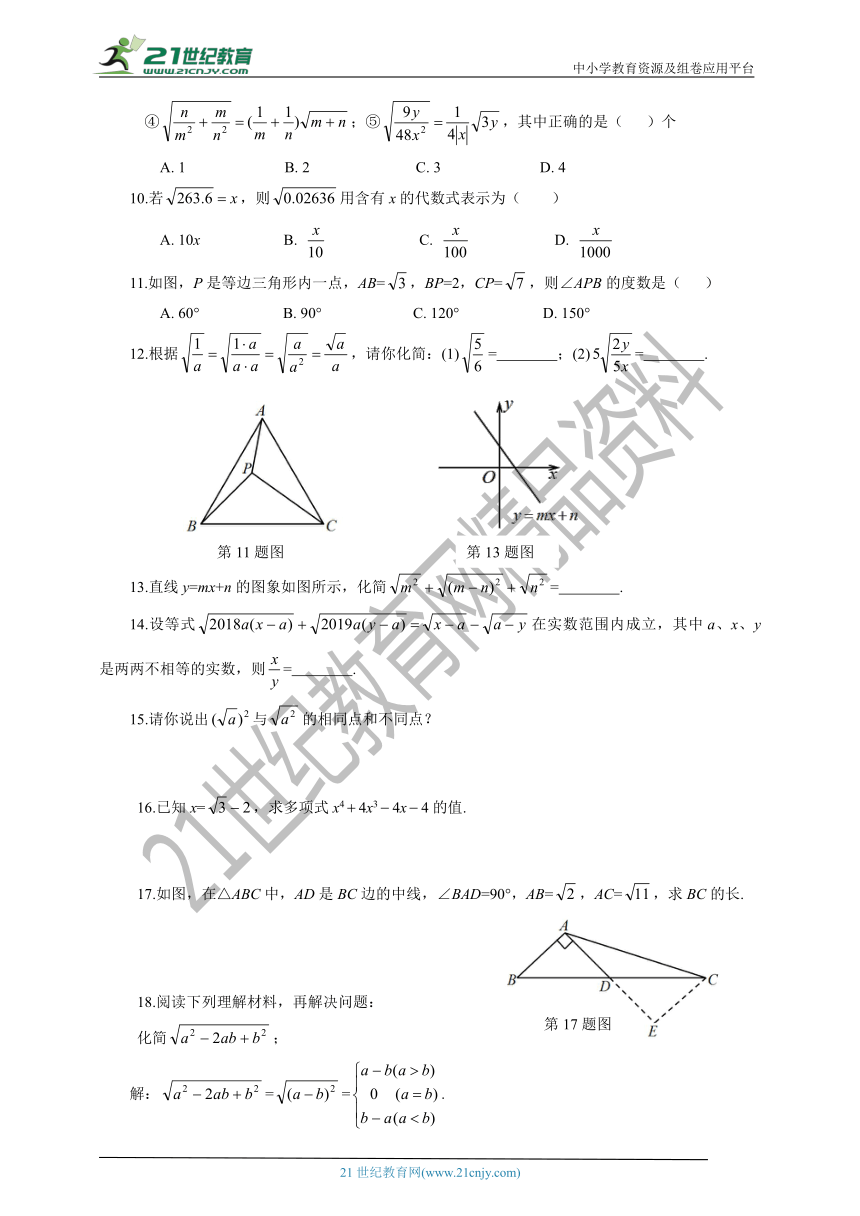
11.如图,P是等边三角形内一点,AB=,BP=2,CP=,则∠APB的度数是( )
A. 60° B. 90° C. 120° D. 150°
12.根据,请你化简:(1)= ;(2)= .
13.直线y=mx+n的图象如图所示,化简= .
14.设等式在实数范围内成立,其中a、x、y是两两不相等的实数,则= .
15.请你说出与的相同点和不同点?
16.已知x=,求多项式x44x34x4的值.
17.如图,在△ABC中,AD是BC边的中线,∠BAD=90°,AB=,AC=,求BC的长.
18.阅读下列理解材料,再解决问题:
化简;
解:==.
根据你的理解,化简下列各题:
(1) ; (2) .
19、观察下列等式:
(1) =,(2) = 2,(3) = 3,(4) = 4,…,
根据你发现的规律填空:
(1)第10个等式是_______________________;
(2)写出你猜想的第n个等式(用含n的代数式表示),并证明其准确性.
【中考链接】
20.2018?河北计算:= .
21.2018?山东滨州20.(5分)观察下列各式:
=1+,=1+,=1+,……
请利用你所发现的规律,
计算++…+其结果为 .
22.2018?山东枣庄15.(4分)我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为.现已知△ABC的三边长分别为1,2,,则△ABC的面积为 .
参考答案
1、A 2、B 3、A 4、C 5、(1) (2) 6、13 9、C 10、C 11、D 12、(1) (2) 13、2(nm) 14、
7.先化简,再求出下面算式的近似值:
(1) (精确到千分位); (2) (精确到0.01)
解:(1);
(2)= .
8.化简
(1) (2) (a≥0, b≥0) (3) (4)
解:(1) =;
(2) =;
(3) =;
(4) ==.
15.请你说出与的相同点和不同点?
解:(1)相同点:与都是非负数;
(2)不同点:①名称不同是a的算术平方根的平方;是a的平方的算术平方根;
②取值范围不同中的a的取值范围是a≥0;中的a的取值范围是全体实数.
③结果不同=a(a≥0); .
16.已知x=,求多项式x44x34x4的值.
解:∵x=,
∴(x2)2=,
即x24x1=0.
x44x34x4
=x44x3x2x24x4
=x2(x24x1)(x24x)4
= 014=3
17.如图,在△ABC中,AD是BC边的中线,∠BAD=90°,AB=,AC=,求BC的长.
解:延长AD到E,使AD=ED,连接CE,
∵点是BC的中点,
∴BD=CD,
在△ABD和△ECD中,
∵
∴△ABD≌△ECD(SAS)
∴AB=CE=
∴∠BAD=∠CED=90°
在Rt△AEC中,
∵AE2=AC2CE2.
∴AE=.
∴AD=.
在Rt△ABD中,
∵BD2=AB2+AD2.
∴AE=.
∴BC=2BD=.
18.阅读下列理解材料,再解决问题:
化简;
解:==.
根据你的理解,化简下列各题:
(1) ; (2) .
解:(1) =
=
=;
(2)
19、观察下列等式:
(1) =,(2) = 2,(3) = 3,(4) = 4,…,
根据你发现的规律填空:
(1)第10个等式是_______________________;
(2)写出你猜想的第n个等式(用含n的代数式表示),并证明其准确性.
解:(1)=10;
(2) =n
证明:=.
【中考链接】
20.2018?河北计算:= .
【考点】22:算术平方根.
【专题】11 :计算题;511:实数.
【分析】先计算被开方数,再根据算术平方根的定义计算可得.
【解答】解:==2,
故答案为:2.
【点评】本题主要考查算术平方根,解题的关键是熟练掌握算术平方根的定义.
21.2018?山东滨州20.(5分)观察下列各式:
=1+,=1+,=1+,……
请利用你所发现的规律,
计算++…+其结果为 .
【分析】直接根据已知数据变化规律进而将原式变形求出答案.
【解答】解:由题意可得:
…
=111…1
=(1…)
=
=.
故答案为:.
【点评】此题主要考查了数字变化规律,正确将原式变形是解题关键.
22.2018?山东枣庄15.(4分)我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为.现已知△ABC的三边长分别为1,2,,则△ABC的面积为 .
【分析】根据题目中的面积公式可以求得△ABC的三边长分别为1,2,的面积,从而可以解答本题.
【解答】解:∵,
∴△ABC的三边长分别为1,2,,则△ABC的面积为:
=1,
故答案为:1.
【点评】本题考查二次根式的应用,解答本题的关键是明确题意,利用题目中的面积公式解答.
第2课时 二次根式的性质(2)
【知识清单】
一、二次根式的性质:?
1. (a≥0,b≥0)
2. (a≥0,b>0)
二、最简二次根式
像、、这样,(1)被开方数不含分母;(2) 被开方数中不含开得尽方的因数或因式,这样的二次根式称为最简二次根式.
在二次根式的运算中,一般要把最后结果化为最简二次根式或有理式.
【经典例题】
例题1、化简下列各式:
(1)= ;(2)= ; (3)= .
【考点】二次根式的性质.?
【分析】利用二次根式的性质进行化简即可.
【解答】(1)= ;
(2)= ;
(3)= .
【点评】本题考查了二次根式的性质:在二次根式的运算中,一般要把最后结果化为最简二次根式或有理式.
例题2、在△ABC中,已知AB=,AC=4,BC=,则△ABC的面积为( )
A. B. C.6 D.
【考点】二次根式的简单应用.
【分析】根据题意可得出BC2=AB2+AC2,再由勾股定理的逆定理可得出△ABC为Rt△,从而得出△ABC的面积.
【解答】∵AB=,AC=4,BC=,
∴AB2=7,AC2=16,BC2=23,
∴BC2=AB2+AC2,
∴△ABC为直角三角形,
∴S△ABC=.
故答案为:选A.
【点评】本题考查了勾股定理的逆定理,已知三角形的三边满足a2+b2=c2,从而得出三角形为直角三角形.
【夯实基础】
1.计算的结果是( )
A. B. ± C. D. ±
2. 若有意义,则不等式axb>0的解集是
A. B. C. D.
3.化简的结果是( )
A. B. C. D.
4. 成立的条件是( )
A. x≥3 B. x≤3 C. 3≤x≤3 D. x=3
5. 把下列根式化成最简二次根式
(1)= ; (2)= .
6. = .
7.先化简,再求出下面算式的近似值:
(1) (精确到千分位); (2) (精确到0.01)
8.化简
(1) (2) (a≥0, b≥0) (3) (4)
【提优特训】
9.化简:①;②;③;
④;⑤,其中正确的是( )个
A. 1 B. 2 C. 3 D. 4
10.若,则用含有x的代数式表示为( )
A. 10x B. C. D.
11.如图,P是等边三角形内一点,AB=,BP=2,CP=,则∠APB的度数是( )
A. 60° B. 90° C. 120° D. 150°
12.根据,请你化简:(1)= ;(2)= .
13.直线y=mx+n的图象如图所示,化简= .
14.设等式在实数范围内成立,其中a、x、y是两两不相等的实数,则= .
15.请你说出与的相同点和不同点?
16.已知x=,求多项式x44x34x4的值.
17.如图,在△ABC中,AD是BC边的中线,∠BAD=90°,AB=,AC=,求BC的长.
18.阅读下列理解材料,再解决问题:
化简;
解:==.
根据你的理解,化简下列各题:
(1) ; (2) .
19、观察下列等式:
(1) =,(2) = 2,(3) = 3,(4) = 4,…,
根据你发现的规律填空:
(1)第10个等式是_______________________;
(2)写出你猜想的第n个等式(用含n的代数式表示),并证明其准确性.
【中考链接】
20.2018?河北计算:= .
21.2018?山东滨州20.(5分)观察下列各式:
=1+,=1+,=1+,……
请利用你所发现的规律,
计算++…+其结果为 .
22.2018?山东枣庄15.(4分)我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为.现已知△ABC的三边长分别为1,2,,则△ABC的面积为 .
参考答案
1、A 2、B 3、A 4、C 5、(1) (2) 6、13 9、C 10、C 11、D 12、(1) (2) 13、2(nm) 14、
7.先化简,再求出下面算式的近似值:
(1) (精确到千分位); (2) (精确到0.01)
解:(1);
(2)= .
8.化简
(1) (2) (a≥0, b≥0) (3) (4)
解:(1) =;
(2) =;
(3) =;
(4) ==.
15.请你说出与的相同点和不同点?
解:(1)相同点:与都是非负数;
(2)不同点:①名称不同是a的算术平方根的平方;是a的平方的算术平方根;
②取值范围不同中的a的取值范围是a≥0;中的a的取值范围是全体实数.
③结果不同=a(a≥0); .
16.已知x=,求多项式x44x34x4的值.
解:∵x=,
∴(x2)2=,
即x24x1=0.
x44x34x4
=x44x3x2x24x4
=x2(x24x1)(x24x)4
= 014=3
17.如图,在△ABC中,AD是BC边的中线,∠BAD=90°,AB=,AC=,求BC的长.
解:延长AD到E,使AD=ED,连接CE,
∵点是BC的中点,
∴BD=CD,
在△ABD和△ECD中,
∵
∴△ABD≌△ECD(SAS)
∴AB=CE=
∴∠BAD=∠CED=90°
在Rt△AEC中,
∵AE2=AC2CE2.
∴AE=.
∴AD=.
在Rt△ABD中,
∵BD2=AB2+AD2.
∴AE=.
∴BC=2BD=.
18.阅读下列理解材料,再解决问题:
化简;
解:==.
根据你的理解,化简下列各题:
(1) ; (2) .
解:(1) =
=
=;
(2)
19、观察下列等式:
(1) =,(2) = 2,(3) = 3,(4) = 4,…,
根据你发现的规律填空:
(1)第10个等式是_______________________;
(2)写出你猜想的第n个等式(用含n的代数式表示),并证明其准确性.
解:(1)=10;
(2) =n
证明:=.
【中考链接】
20.2018?河北计算:= .
【考点】22:算术平方根.
【专题】11 :计算题;511:实数.
【分析】先计算被开方数,再根据算术平方根的定义计算可得.
【解答】解:==2,
故答案为:2.
【点评】本题主要考查算术平方根,解题的关键是熟练掌握算术平方根的定义.
21.2018?山东滨州20.(5分)观察下列各式:
=1+,=1+,=1+,……
请利用你所发现的规律,
计算++…+其结果为 .
【分析】直接根据已知数据变化规律进而将原式变形求出答案.
【解答】解:由题意可得:
…
=111…1
=(1…)
=
=.
故答案为:.
【点评】此题主要考查了数字变化规律,正确将原式变形是解题关键.
22.2018?山东枣庄15.(4分)我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为.现已知△ABC的三边长分别为1,2,,则△ABC的面积为 .
【分析】根据题目中的面积公式可以求得△ABC的三边长分别为1,2,的面积,从而可以解答本题.
【解答】解:∵,
∴△ABC的三边长分别为1,2,,则△ABC的面积为:
=1,
故答案为:1.
【点评】本题考查二次根式的应用,解答本题的关键是明确题意,利用题目中的面积公式解答.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
