浙教版九年级数学下第二章 直线与圆的位置关系 单元检测
文档属性
| 名称 | 浙教版九年级数学下第二章 直线与圆的位置关系 单元检测 |  | |
| 格式 | zip | ||
| 文件大小 | 370.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 13:28:57 | ||
图片预览



文档简介
浙教版九年级数学下第二章直线与圆的位置关系
单元检测
题号 一 二 三 总分
得分
第Ⅰ卷(选择题)
评卷人 得 分
一、选择题(共10小题,3*10=30)
1.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25° B.30° C.40° D.45°
2.如图,在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
3.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
4.如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
A. B. C. D.
5.如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长是( )
A.5 B.5 C.5 D.
6.如图,在Rt△ABC中,∠A=90°,BC=2 ,以BC的中点O为圆心的⊙O分别与AB,AC相切于D,E两点,则的长为( )
A. B. C.π D.2π
7.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2 ≤b≤2
C.-2 <b<2 D.-2 <b<2
8.如图,⊙O的半径为2,点O到直线l的距离为3,P是直线l上的一个动点,PB切⊙O于点B,则PB长的最小值为( )
A. B. C.3 D.2
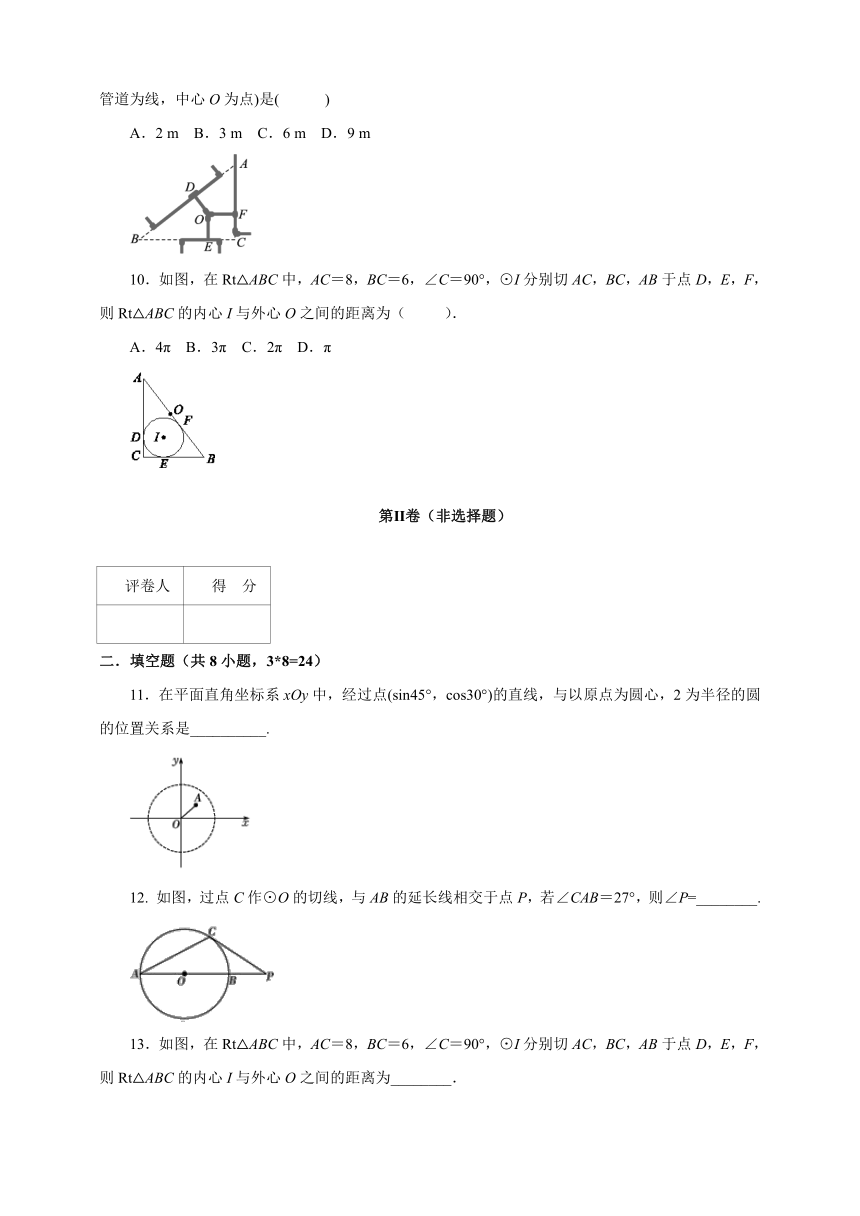
9.下图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边长分别为6 m和8 m.按照输油中心O到三条支路的距离相等来连结管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A.2 m B.3 m C.6 m D.9 m
10.如图,在Rt△ABC中,AC=8,BC=6,∠C=90°,⊙I分别切AC,BC,AB于点D,E,F,则Rt△ABC的内心I与外心O之间的距离为( ).
A.4π B.3π C.2π D.π
第Ⅱ卷(非选择题)
评卷人 得 分
二.填空题(共8小题,3*8=24)
11.在平面直角坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是__________.
12. 如图,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,则∠P=________.
13.如图,在Rt△ABC中,AC=8,BC=6,∠C=90°,⊙I分别切AC,BC,AB于点D,E,F,则Rt△ABC的内心I与外心O之间的距离为________.
14.如图,在平行四边形ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则弧FE的长为________.
15.如图,AT切⊙O于点A,AB是⊙O的直径,若∠ABT=40°,则∠ATB=________°.
16.如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°.
17.如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,P为直线y=-x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是________.
18.如图,已知⊙C的半径为3,圆外一定点O满足OC=5,P为⊙C上一动点,经过点O的直线l上有两点A,B且OA=OB, ∠APB=90°,l不经过点C,则AB的最小值为________.
评卷人 得 分
三.解答题(共7小题, 46分)
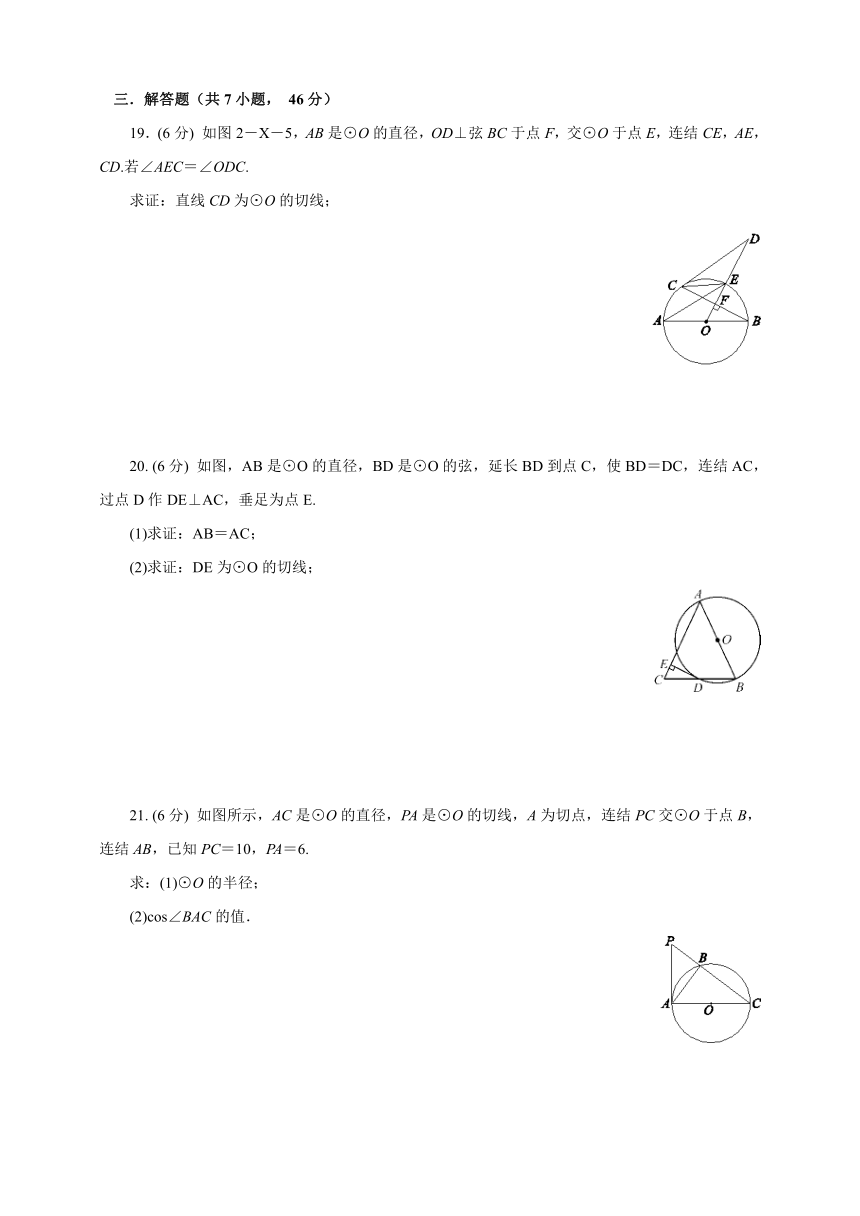
19.(6分) 如图2-X-5,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE,AE,CD.若∠AEC=∠ODC.
求证:直线CD为⊙O的切线;
20. (6分) 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使BD=DC,连结AC,过点D作DE⊥AC,垂足为点E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
21. (6分) 如图所示,AC是⊙O的直径,PA是⊙O的切线,A为切点,连结PC交⊙O于点B,连结AB,已知PC=10,PA=6.
求:(1)⊙O的半径;
(2)cos∠BAC的值.
22.如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
23.如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.
24.如图,在△ABC中,AC=BC,∠ACB=90°, ⊙O(圆心O在△ABC内部)经过B,C两点,交AB于点E,经过点E作⊙O的切线交AC于点F,连结CO并延长交AB于点G,作ED∥AC交CG于点D.
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的长.
25.如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数;
②若⊙O的半径为2 ,求线段EF的长.
参考答案
1-5 CAABC
6-10 BDBCD
11. 相交
12. 36°
13.
14. π
15. 50
16. 120
17. 2
18. 4
19. 解:连结CO.∵圆周角∠AEC与∠ABC所对的弧相同,∴∠ABC=∠AEC.又∠AEC=∠ODC,∴∠ABC=∠ODC.∵OC=OB,OD⊥BC,∴∠OCB=∠OBC,且∠OCB+∠COD=90°.∴∠ODC+∠COD=90°,∴∠OCD=180°-∠ODC-∠COD=90°,即OC⊥CD.又OC为⊙O的半径,∴直线CD为⊙O的切线.
20. 解:(1)连结AD,∵AB是⊙O的直径,∴∠ADB=90°,又BD=CD,∴AD是BC的垂直平分线,∴AB=AC
(2)连结OD,∵O,D分别是AB,BC的中点,∴OD∥AC,又DE⊥AC,∴OD⊥DE,∴DE为⊙O的切线
21.解:(1)∵PA是⊙O的切线,AC为⊙O的直径,∴PA⊥AC.在Rt△ACP中,PA=6,PC=10,∴AC==8,∴AO=AC=4.故⊙O的半径为4.
(2)∵AC为⊙O的直径,∴∠ABC=90°.又∵∠PAC=90°,∠ACB=∠PCA,∴△ABC∽△PAC,∴∠BAC=∠P,∴cos∠BAC=cosP===.
22.解:(1)证明:如图,连结OD,∵DE是⊙O的切线,∴∠ODE=90°,∴∠ADE+∠BDO=90°.∵∠ACB=90°,∴∠A+∠B=90°.∵OD=OB,∴∠B=∠BDO.∴∠A=∠ADE.
(2)如图,连结CD,∵∠ADE=∠A,∴AE=DE.∵BC是⊙O的直径,∠ACB=90°.∴EC是⊙O的切线,∴DE=EC,∴AE=EC.∵DE=10,∴AC=2DE=20.在Rt△ADC中,DC==12.设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2-202,∴x2+122=(x+16)2-202,解得x=9,∴BC==15.
23.解:(1)在Rt△ABC中,∵BC=,AC=3,∴AB==2 .∵BC⊥OC,∴BC是⊙O的切线.又∵⊙O与斜边AB相切于点D,∴BD=BC=,∴AD=AB-BD=2 -=.
(2)在Rt△ABC中,∵sinA===,∴∠A=30°.∵⊙O与斜边AB相切于点D,∴OD⊥AB,∴∠AOD=90°-∠A=60°.∵=tanA=tan30°,∴=,∴OD=1,∴S阴影==.
24.解:(1)证明:如图,连结OE.∵AC=BC,∠ACB=90°,∴∠B=45°,∴∠COE=2∠B=90°.∵EF是⊙O的切线,∴OE⊥EF,∴∠FEO=90°,∴∠FEO+∠COE=180°,∴EF∥CD.又∵ED∥AC,∴四边形CDEF是平行四边形.
(2)如图,过点G作GH⊥BC,垂足为H.∵四边形CDEF是平行四边形,∴∠DEF=∠1.又∵GH⊥BC,∴∠GHB=∠ACB=90°,∴AC∥GH,∴∠1=∠2,∴∠DEF=∠2.又∵tan∠DEF=2,∴在Rt△CHG中,tan∠2==2.∵在Rt△BHG中,∠B=45°,∴GH=BH,∴=2.又∵BC=3,∴CH=2,BH=1.在Rt△BHG中,由勾股定理,得BG=.
25.解:(1)证明:∵CD是⊙O的切线,∴OC⊥CD.又∵AD⊥CD,∴OC∥AD,∴∠DAC=∠ACO.∵OA=OC,∴∠OAC=∠ACO,∴∠DAC=∠OAC,∴AC平分∠DAO.
(2)①∵OC∥AD,∴∠EOC=∠DAO=105°,∴∠OCE=180°-∠EOC-∠E=180°-105°-30°=45°.②如图,过点O作OG⊥CE于点G,∴FG=CG.在Rt△OGC中,OC=2 ,∠OCE=45°,∴OG=CG=OCsin45°=2 ×=2,∴FG=CG=2.在Rt△OGE中,OG=2,∠E=30°,∴EG===2 ,∴EF=EG-FG=2 -2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
单元检测
题号 一 二 三 总分
得分
第Ⅰ卷(选择题)
评卷人 得 分
一、选择题(共10小题,3*10=30)
1.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25° B.30° C.40° D.45°
2.如图,在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
3.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
4.如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
A. B. C. D.
5.如图,AB是⊙O的直径,PA切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长是( )
A.5 B.5 C.5 D.
6.如图,在Rt△ABC中,∠A=90°,BC=2 ,以BC的中点O为圆心的⊙O分别与AB,AC相切于D,E两点,则的长为( )
A. B. C.π D.2π
7.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2 ≤b≤2
C.-2 <b<2 D.-2 <b<2
8.如图,⊙O的半径为2,点O到直线l的距离为3,P是直线l上的一个动点,PB切⊙O于点B,则PB长的最小值为( )
A. B. C.3 D.2
9.下图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边长分别为6 m和8 m.按照输油中心O到三条支路的距离相等来连结管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A.2 m B.3 m C.6 m D.9 m
10.如图,在Rt△ABC中,AC=8,BC=6,∠C=90°,⊙I分别切AC,BC,AB于点D,E,F,则Rt△ABC的内心I与外心O之间的距离为( ).
A.4π B.3π C.2π D.π
第Ⅱ卷(非选择题)
评卷人 得 分
二.填空题(共8小题,3*8=24)
11.在平面直角坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是__________.
12. 如图,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,则∠P=________.
13.如图,在Rt△ABC中,AC=8,BC=6,∠C=90°,⊙I分别切AC,BC,AB于点D,E,F,则Rt△ABC的内心I与外心O之间的距离为________.
14.如图,在平行四边形ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则弧FE的长为________.
15.如图,AT切⊙O于点A,AB是⊙O的直径,若∠ABT=40°,则∠ATB=________°.
16.如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°.
17.如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,P为直线y=-x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是________.
18.如图,已知⊙C的半径为3,圆外一定点O满足OC=5,P为⊙C上一动点,经过点O的直线l上有两点A,B且OA=OB, ∠APB=90°,l不经过点C,则AB的最小值为________.
评卷人 得 分
三.解答题(共7小题, 46分)
19.(6分) 如图2-X-5,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE,AE,CD.若∠AEC=∠ODC.
求证:直线CD为⊙O的切线;
20. (6分) 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使BD=DC,连结AC,过点D作DE⊥AC,垂足为点E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
21. (6分) 如图所示,AC是⊙O的直径,PA是⊙O的切线,A为切点,连结PC交⊙O于点B,连结AB,已知PC=10,PA=6.
求:(1)⊙O的半径;
(2)cos∠BAC的值.
22.如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
23.如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.
24.如图,在△ABC中,AC=BC,∠ACB=90°, ⊙O(圆心O在△ABC内部)经过B,C两点,交AB于点E,经过点E作⊙O的切线交AC于点F,连结CO并延长交AB于点G,作ED∥AC交CG于点D.
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的长.
25.如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数;
②若⊙O的半径为2 ,求线段EF的长.
参考答案
1-5 CAABC
6-10 BDBCD
11. 相交
12. 36°
13.
14. π
15. 50
16. 120
17. 2
18. 4
19. 解:连结CO.∵圆周角∠AEC与∠ABC所对的弧相同,∴∠ABC=∠AEC.又∠AEC=∠ODC,∴∠ABC=∠ODC.∵OC=OB,OD⊥BC,∴∠OCB=∠OBC,且∠OCB+∠COD=90°.∴∠ODC+∠COD=90°,∴∠OCD=180°-∠ODC-∠COD=90°,即OC⊥CD.又OC为⊙O的半径,∴直线CD为⊙O的切线.
20. 解:(1)连结AD,∵AB是⊙O的直径,∴∠ADB=90°,又BD=CD,∴AD是BC的垂直平分线,∴AB=AC
(2)连结OD,∵O,D分别是AB,BC的中点,∴OD∥AC,又DE⊥AC,∴OD⊥DE,∴DE为⊙O的切线
21.解:(1)∵PA是⊙O的切线,AC为⊙O的直径,∴PA⊥AC.在Rt△ACP中,PA=6,PC=10,∴AC==8,∴AO=AC=4.故⊙O的半径为4.
(2)∵AC为⊙O的直径,∴∠ABC=90°.又∵∠PAC=90°,∠ACB=∠PCA,∴△ABC∽△PAC,∴∠BAC=∠P,∴cos∠BAC=cosP===.
22.解:(1)证明:如图,连结OD,∵DE是⊙O的切线,∴∠ODE=90°,∴∠ADE+∠BDO=90°.∵∠ACB=90°,∴∠A+∠B=90°.∵OD=OB,∴∠B=∠BDO.∴∠A=∠ADE.
(2)如图,连结CD,∵∠ADE=∠A,∴AE=DE.∵BC是⊙O的直径,∠ACB=90°.∴EC是⊙O的切线,∴DE=EC,∴AE=EC.∵DE=10,∴AC=2DE=20.在Rt△ADC中,DC==12.设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2-202,∴x2+122=(x+16)2-202,解得x=9,∴BC==15.
23.解:(1)在Rt△ABC中,∵BC=,AC=3,∴AB==2 .∵BC⊥OC,∴BC是⊙O的切线.又∵⊙O与斜边AB相切于点D,∴BD=BC=,∴AD=AB-BD=2 -=.
(2)在Rt△ABC中,∵sinA===,∴∠A=30°.∵⊙O与斜边AB相切于点D,∴OD⊥AB,∴∠AOD=90°-∠A=60°.∵=tanA=tan30°,∴=,∴OD=1,∴S阴影==.
24.解:(1)证明:如图,连结OE.∵AC=BC,∠ACB=90°,∴∠B=45°,∴∠COE=2∠B=90°.∵EF是⊙O的切线,∴OE⊥EF,∴∠FEO=90°,∴∠FEO+∠COE=180°,∴EF∥CD.又∵ED∥AC,∴四边形CDEF是平行四边形.
(2)如图,过点G作GH⊥BC,垂足为H.∵四边形CDEF是平行四边形,∴∠DEF=∠1.又∵GH⊥BC,∴∠GHB=∠ACB=90°,∴AC∥GH,∴∠1=∠2,∴∠DEF=∠2.又∵tan∠DEF=2,∴在Rt△CHG中,tan∠2==2.∵在Rt△BHG中,∠B=45°,∴GH=BH,∴=2.又∵BC=3,∴CH=2,BH=1.在Rt△BHG中,由勾股定理,得BG=.
25.解:(1)证明:∵CD是⊙O的切线,∴OC⊥CD.又∵AD⊥CD,∴OC∥AD,∴∠DAC=∠ACO.∵OA=OC,∴∠OAC=∠ACO,∴∠DAC=∠OAC,∴AC平分∠DAO.
(2)①∵OC∥AD,∴∠EOC=∠DAO=105°,∴∠OCE=180°-∠EOC-∠E=180°-105°-30°=45°.②如图,过点O作OG⊥CE于点G,∴FG=CG.在Rt△OGC中,OC=2 ,∠OCE=45°,∴OG=CG=OCsin45°=2 ×=2,∴FG=CG=2.在Rt△OGE中,OG=2,∠E=30°,∴EG===2 ,∴EF=EG-FG=2 -2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
