2.3.2 一元二次方程的应用(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 2.3.2 一元二次方程的应用(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 300.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-02 00:00:00 | ||
图片预览



文档简介
浙江版八年级数学下册第2章2.3一元二次方程的应用
第2课时 一元二次方程的应用(2)
【知识清单】
一、列一元二次方程解应用题的一般步骤:与列一元一次方程解应用题的步骤类似,列一元二次方程方程解实际问题的一般步骤也可归纳为:“审、找、设、列、解、验、答”七个步骤.
(1)审:审清题意,弄清已知量与未知量;
(2)找:找出等量关系;
(3)设:设未知数,有直接和间接两种设法,因题而异;
(4)列:列出一元二次方程;
(5)解:求出所列方程的解;
(6)验:①检验方程的解是否正确,②是否符合题意;
(7)答:作答.
二、列方程解决实际生活中有关面积计算问题:
1.不规则图形面积的求法一般转化为规则图形来计算,常用的方法是割补法;平移、旋转等几何变换在平面图形面积计算问题中也常常用到,主要起到转化作用.
2.平面内距离计算问题主要是构造直角三角形,利用勾股定理进行计算.
【经典例题】
例题1、用32cm长的铁丝做成一个长方形,用36cm长的铁丝做成一个有一边长为10cm的等腰三角形,如果长方形的面积与等腰三角形的面积相等,则长方形的边长为( )
A、4cm、12cm B、6cm、10cm C、4cm、12cm或6cm、10cm D、无法确定
【考点】一元二次方程的应用.
【分析】因为本题中等腰三角形的边长不确定,所以需分情况讨论,分别求出面积.
【解答】等腰三角形周长为36cm,其中一边长为10cm,那么,有两种情况:
(1)腰长为10cm时,则底边长为12cm,此时由勾股定理可得高长为8cm,则三角形面积
为48 cm 2.所以长方形的面积也为48cm 2.
设长方形的两边为a和b,那么ab=48,a+b=32÷2=16,
则a=16b,把a=16b代入ab=48,
整理得b216b+48=0,
解得,b1=4,b2=12,
∴a1=12,a2=4.
∴长方形两边分别为12cm和4cm.
(2)底边长为10cm,那么腰长为13cm,由勾股定理可得高长为12cm,则三角形面积为60cm 2.
所以长方形的面积也为60cm2.同样,ab=60,a+b=16,则长方形的两边分别为6cm和10cm.
故选C.
【点评】本题涉及长方形的周长和面积,熟练掌握一元二次方程的解法是关键.
例题2、MN是一面长28m的墙,用长48m的篱笆,围成一个一面是墙,中间隔着一道篱笆的长方形温室大棚ABCD,已知温室大棚的设计面积为180m2,求温室大棚的宽AB应当是多少?
【考点】一元二次方程的应用.
【分析】?设温室大棚的宽为xm,则AB=x,BC=483x,利用面积公式表示出长方形的面积即可列出方程,根据实际情况求出x的值即可.
【解答】设温室大棚的宽为xm,那么它的长是(483x)m 根据题意得方程
x(483x)=180,
即x216x+60=0.
解得x1=6,x2=10,
当x=6时,483x=30>28,
所以x=6(不合题意,舍去).
答:温室大棚的宽为10m.
【点评】考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题的关键是垂直于墙的有三道篱笆.
【夯实基础】
1、老张有一块长65cm,宽60cm的长方形铁皮,准备制作一个工具箱,如图,他将长方形铁皮的四个角各剪掉一个边长xcm的正方形后,剩余的部分刚好能围成一个底面积为Scm2的无盖长方形工具箱,根据题意写出S的函数表达式为( )
A. S=(65x)(60x) B. S=80×704x2
C. S=(802x)(702x) D. S=80×704x2(70+80)x
2、如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了3m,另一边减少了4m,
剩余一块面积为20m2的长方形空地,则原正方形空地的边长是( )
A.7m B.8m C.9m D.10m
3、如图,长方形ABCD的周长是24cm,以AB、AD为边向外作正方形ABEF和正方形
ADGH,若正方形ABEF和ADGH的面积之和为80cm2,那么长方形ABCD的面积是( )
A. 24cm2 B.28cm2 C. 32cm2 D. 36cm2
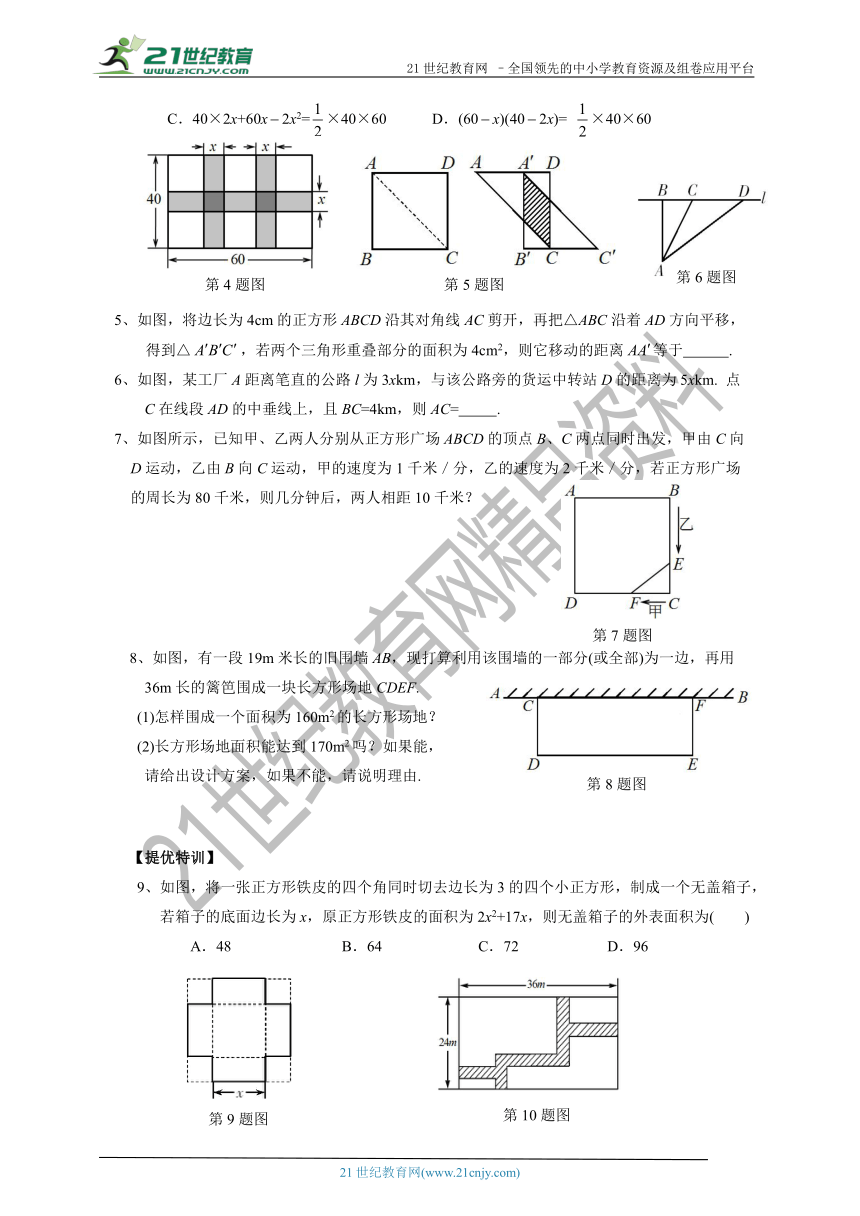
4、如图,在长为60米,宽为40米的长方形场地上修建1横2纵三条宽度相等的甬道,其余部分为绿地,若绿化面积为长方形面积的一半,则甬道的宽应为多少米?设甬道的宽为x米,则列出的方程不正确的为( )
A.(602x)(40x)=×40×60 B.40×6040×2x60x+2x2=×40×60
C.40×2x+60x2x2=×40×60 D.(60x)(402x)= ×40×60
5、如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,
得到△,若两个三角形重叠部分的面积为4cm2,则它移动的距离等于 .
6、如图,某工厂A距离笔直的公路l为3xkm,与该公路旁的货运中转站D的距离为5xkm. 点
C在线段AD的中垂线上,且BC=4km,则AC= .
7、如图所示,已知甲、乙两人分别从正方形广场ABCD的顶点B、C两点同时出发,甲由C向
D运动,乙由B向C运动,甲的速度为1千米/分,乙的速度为2千米/分,若正方形广场
的周长为80千米,则几分钟后,两人相距10千米?
8、如图,有一段19m米长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用
36m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160m2的长方形场地?
(2)长方形场地面积能达到170m2吗?如果能,
请给出设计方案,如果不能,请说明理由.
【提优特训】
9、如图,将一张正方形铁皮的四个角同时切去边长为3的四个小正方形,制成一个无盖箱子,
若箱子的底面边长为x,原正方形铁皮的面积为2x2+17x,则无盖箱子的外表面积为( )
A.48 B.64 C.72 D.96
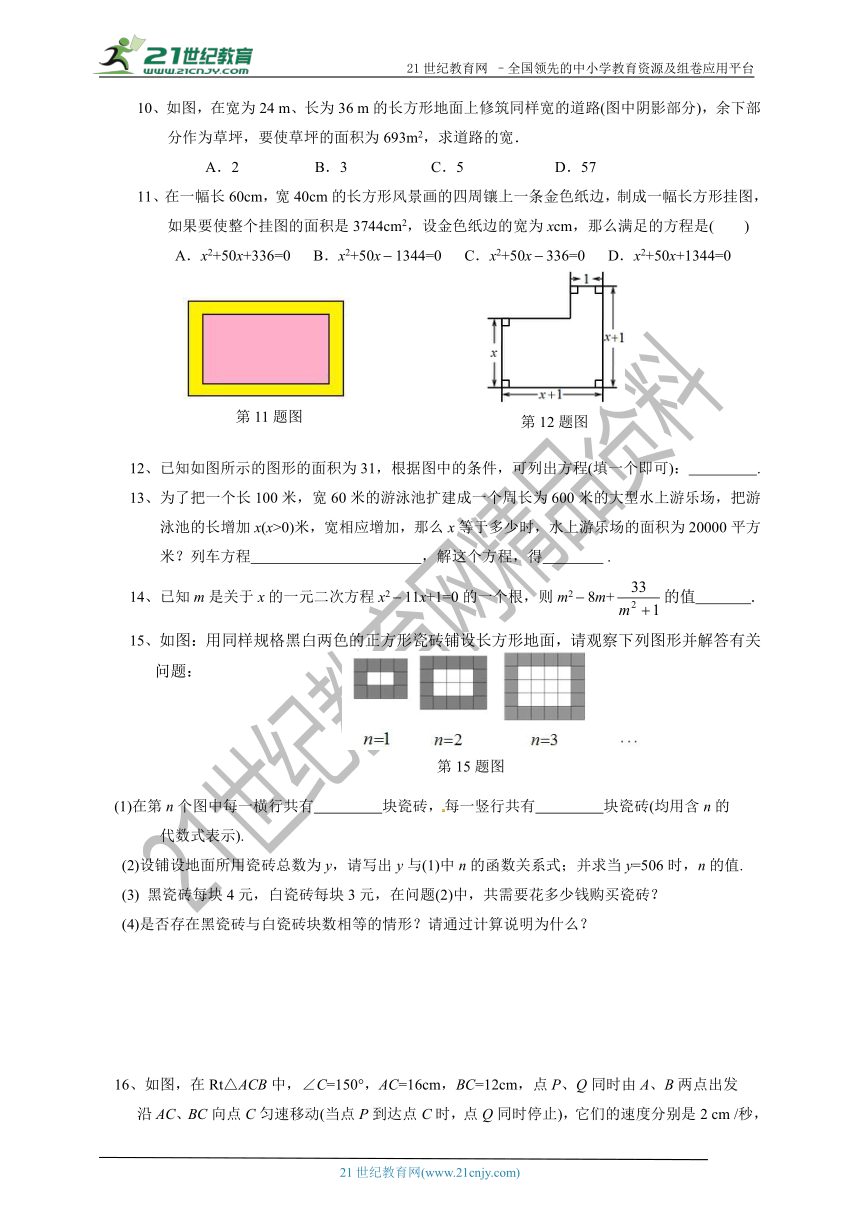
10、如图,在宽为24 m、长为36 m的长方形地面上修筑同样宽的道路(图中阴影部分),余下部分作为草坪,要使草坪的面积为693m2,求道路的宽.
A.2 B.3 C.5 D.57
11、在一幅长60cm,宽40cm的长方形风景画的四周镶上一条金色纸边,制成一幅长方形挂图,如果要使整个挂图的面积是3744cm2,设金色纸边的宽为xcm,那么满足的方程是( )
A.x2+50x+336=0 B.x2+50x1344=0 C.x2+50x336=0 D.x2+50x+1344=0
12、已知如图所示的图形的面积为31,根据图中的条件,可列出方程(填一个即可): .
13、为了把一个长100米,宽60米的游泳池扩建成一个周长为600米的大型水上游乐场,把游泳池的长增加x(x>0)米,宽相应增加,那么x等于多少时,水上游乐场的面积为20000平方
米?列车方程? ? ?,解这个方程,得?? ?.
14、已知m是关于x的一元二次方程x211x+1=0的一个根,则m28m+的值 .
15、如图:用同样规格黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形并解答有关问题:
(1)在第n个图中每一横行共有 块瓷砖,每一竖行共有 块瓷砖(均用含n的
代数式表示).
(2)设铺设地面所用瓷砖总数为y,请写出y与(1)中n的函数关系式;并求当y=506时,n的值.
(3) 黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明为什么?
16、如图,在Rt△ACB中,∠C=150°,AC=16cm,BC=12cm,点P、Q同时由A、B两点出发
沿AC、BC向点C匀速移动(当点P到达点C时,点Q同时停止),它们的速度分别是2 cm /秒,
1 cm /秒.
问:(1)写出△PCQ的面积S△PCQ与时间t的函数关系?
(2)几秒后S△PCQ =S△ACB?
17、将一条长为32cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于30cm2吗?若能,求出两段铁丝的长度;若不能,请说
明理由.
(3)则这两个正方形面积之和的最小值是多少cm2.
18、在一块长16m,宽12m的长方形荒地上,要建造一个花园,要求花园所占面积为荒地面积的
一半.下面分别是小明和小颖的设计方案.
小明的设计方案如图1:其中花园四周小路的宽度相等(阴影部分).通过解方程,可得到小路的宽
为2m或12m.
小颖的设计方案如图2:其中花园中每个角上的扇形都相同(阴影部分).
(1)你认为小明的结果对吗?请说明理由;
(2)请你帮助小颖求出图中的x(精确到0.1m);
(3)你还有其他的设计方案吗?请在图3中画出你所设计的草图(标上相关数据).
【中考链接】
19、(2018?广西北海)如图,矩形纸片 ABCD,AB=4,BC=3,点 P 在 BC 边上,将△CDP 沿 DP 折叠,点 C落在点 E 处,PE、DE 分别交 AB 于点 O、F,且 OP=OF,则EF的值为( )
A. B. C.1 D.
20、(2018?大连)8.(3.00分)如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为(? ?)
A.10×64×6x=32? B.(102x)(62x)=32?
C.(10x)(6x)=32 D.10×64x2=32?
21、(2018?山东日照)为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为 .
22、(2018?江苏常州)26.(10.00分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x22x=0,可以通过因式分解把它转化为x(x2+x2)=0,解方程x=0和x2+x2=0,可得方程x3+x22x=0的解.
(1)问题:方程x3+x22x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程=x的解;
(3)应用:如图,已知长方形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
参考答案
1、C 2、B 3、C 4、D 5、2cm 6、 9、B 10、B 11、C 12、x2+x+1=31
13、(100+x)(200x)=20000 ,x=100 14、32 19、A 20、B, 21、x(x+40)=1200
7、如图所示,已知甲、乙两人分别从正方形广场ABCD的顶点B、C两点同时出发,甲由C向
D运动,乙由B向C运动,甲的速度为1千米/分,乙的速度为2千米/分,若正方形广场
的周长为80千米,则几分钟后,两人相距10千米?
解:设x分钟后,两个相距10千米,
则CF=x千米,CE=(202x)千米,
由勾股定理得(0≤x≤10)
x2+(202x)2=102
解得x1=6,x2=10.
当x=6时, CF=6,EC=2012=8<20符合题意
当x=10时,CF=10,EC=2020=0不符合题意,舍去
答:6分钟后,两人相距10千米
8、如图,有一段19m米长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用
36m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160m2的长方形场地?
(2)长方形场地面积能达到170m2吗?如果能,
请给出设计方案,如果不能,请说明理由.
解: (1)设CD=xm,则DE=(362x)m,
依题意得x(362x)=160,
整理得x218x+80=0,
解得x1=10,x2=8,
当x1=10时,362x=16,当x2=8时,362x=20>19(不合题意舍去),
∴能围成一个长16m,宽10m的长方形场地.
(2)设CD=ym,则DE=(362y)m,
依题意得y(362y)=170,整理得y218y+85=0,
△=(18)24×1×85=16<0,故方程没有实数根,
∴长方形场地面积不能达到170m2.
15、如图:用同样规格黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形并解答有关问题:
(1)在第n个图中每一横行共有 块瓷砖,每一竖行共有 块瓷砖(均用含n的
代数式表示).
(2)设铺设地面所用瓷砖总数为y,请写出y与(1)中n的函数关系式;并求当y=506时,n的值.
(3) 黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明为什么?
解:(1)通过观察图形可知,n+3,n+2
(2)当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,①每个图形需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形
数的平方加上图形数;②每个需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等
于图形数的4倍加上6.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为n2+n;
黑瓷砖的块数可用含n的代数式表示为4n+6.
观察图形可知,由题意,得y=(n+3)(n+2)
当y=506时,(n +3)(n+2)=506,
解之,n1 =25(舍去) ,n2 =20.
并求当y=506时, n的值为20块.
在问题(2)中,购买瓷砖共花费:420×3+86×4=1604(元)
(3)每一横行有白砖(n+1)块,每一竖列有白砖n块,因而白砖总数是n(n+1)块,n=20时,需白砖为
20×21=420(块),需黑砖数为86(块).
在问题(2)中,购买瓷砖共花费:420×3+86×4=1604(元).
答:共花1604元钱购买瓷砖.
(4)n(n+1)=4n+6.
解得n= .
因为n不为整数.
∴不存在黑白瓷砖块数相等的情形.
16、如图,在Rt△ACB中,∠C=150°,AC=16cm,BC=12cm,点P、Q同时由A、B两点出发
沿AC、BC向点C匀速移动(当点P到达点C时,点Q同时停止),它们的速度分别是2 cm /秒,
1 cm /秒.
问:(1)写出△PCQ的面积S△PCQ与时间t的函数关系?
(2)几秒后S△PCQ =S△ACB?
解:(1)设t秒后,PC=AC-AP=16-2t,CQ=BCBQ=12t,
∵∠C=150°,
∴∠PCE=180°150°=30°.
∴PE=PC=8t,AD=AC=8.
∴S△PCQ=PE·CQ=(8t)( 12t)=t210t+48.
(2) 设x秒后S△PCQ =S△ACB?
∵△ABC面积为×AD×BC=×8×12=48,
∴x210x+48=×48,
解得x1=4,x2=16(不合题意舍去)
4秒后S△PCQ =S△ACB.
17、将一条长为32cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于30cm2吗?若能,求出两段铁丝的长度;若不能,请说
明理由.
(3)则这两个正方形面积之和的最小值是多少cm2.
解:(1)设其中一个正方形的边长为xcm,则另一个正方形的边长为(8x)cm,
依题意列方程得x2+(8x)2=34,
整理得:x28x+15=0,(x3)(x5)=0,
解方程得x1=3,x2=5,
3×4=12cm,3212=20cm;
或5×4=20cm,3220=12cm.
因此这段铁丝剪成两段后的长度分别是12cm、20cm;
(2)两个正方形的面积之和不可能等于12cm2.
由(1)可知x2+(8x)2=30,
化简后得2x216x+34=0,
∵△=(16)24×2×34=16<0,
∴方程无实数解;
所以两个正方形的面积之和不可能等于30cm2.
(3)设两个正方形的面积和为y,
则y=x2+(8x)2=2(x4)2+32,
∴当x=4时,y的最小值=32,
∴这两个正方形面积之和的最小值是32cm2.
18、在一块长16m,宽12m的长方形荒地上,要建造一个花园,要求花园所占面积为荒地面积的
一半.下面分别是小明和小颖的设计方案.
小明的设计方案如图1:其中花园四周小路的宽度相等(阴影部分).通过解方程,可得到小路的宽
为2m或12m.
小颖的设计方案如图2:其中花园中每个角上的扇形都相同(阴影部分).
(1)你认为小明的结果对吗?请说明理由;
(2)请你帮助小颖求出图中的x(精确到0.1m);
(3)你还有其他的设计方案吗?请在图3中画出你所设计的草图(标上相关数据).
解:(1)小明的结果不对.
设小路宽xm,则得方程(162x)(122x)=×16×12
解得:x1=2,x2=12
而荒地的宽为12m,若小路宽为12m,不符合实际情况,故x2=12m不合题意
(2)由题意得:=×16×12
x2=,x≈5.5m .
答:小颖的设计方案中扇形的半径约为5.5m
(3)
22、(2018?江苏常州)26.(10.00分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x22x=0,可以通过因式分解把它转化为x(x2+x2)=0,解方程x=0和x2+x2=0,可得方程x3+x22x=0的解.
(1)问题:方程x3+x22x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程=x的解;
(3)应用:如图,已知长方形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
【分析】(1)因式分解多项式,然后得结论;
(2)两边平方,把无理方程转化为整式方程,求解,注意验根;
(3)设AP的长为xm,根据勾股定理和BP+CP=10,可列出方程,由于方程含有根号,两边平方,把无理方程转化为整式方程,求解,
【解答】解:(1)x3+x22x=0,
x(x2+x2)=0,
x(x+2)(x1)=0
所以x=0或x+2=0或x1=0
∴x1=0,x2=2,x3=1;
故答案为:2,1;
(2)=x,
方程的两边平方,得2x+3=x2
即x22x3=0
(x3)(x+1)=0
∴x3=0或x+1=0
∴x1=3,x2=1,
当x=1时,==1≠1,
所以1不是原方程的解.
所以方程=x的解是x=3;
(3)因为四边形ABCD是长方形,
所以∠A=∠D=90°,AB=CD=3m
设AP=xm,则PD=(8x)m
因为BP+CP=10,
BP=,CP=
∴=10
∴
两边平方,得(8x)2+9=10020+9+x2
整理,得5=4x+9
两边平方并整理,得x28x+16=0
即(x4)2=0
所以x=4.
经检验,x=4是方程的解.
答:AP的长为4m.
【点评】本题考查了转化的思想方法,一元二次方程的解法.解无理方程是注意到验根.解决(3)时,根据勾股定理和绳长,列出方程是关键.
第2课时 一元二次方程的应用(2)
【知识清单】
一、列一元二次方程解应用题的一般步骤:与列一元一次方程解应用题的步骤类似,列一元二次方程方程解实际问题的一般步骤也可归纳为:“审、找、设、列、解、验、答”七个步骤.
(1)审:审清题意,弄清已知量与未知量;
(2)找:找出等量关系;
(3)设:设未知数,有直接和间接两种设法,因题而异;
(4)列:列出一元二次方程;
(5)解:求出所列方程的解;
(6)验:①检验方程的解是否正确,②是否符合题意;
(7)答:作答.
二、列方程解决实际生活中有关面积计算问题:
1.不规则图形面积的求法一般转化为规则图形来计算,常用的方法是割补法;平移、旋转等几何变换在平面图形面积计算问题中也常常用到,主要起到转化作用.
2.平面内距离计算问题主要是构造直角三角形,利用勾股定理进行计算.
【经典例题】
例题1、用32cm长的铁丝做成一个长方形,用36cm长的铁丝做成一个有一边长为10cm的等腰三角形,如果长方形的面积与等腰三角形的面积相等,则长方形的边长为( )
A、4cm、12cm B、6cm、10cm C、4cm、12cm或6cm、10cm D、无法确定
【考点】一元二次方程的应用.
【分析】因为本题中等腰三角形的边长不确定,所以需分情况讨论,分别求出面积.
【解答】等腰三角形周长为36cm,其中一边长为10cm,那么,有两种情况:
(1)腰长为10cm时,则底边长为12cm,此时由勾股定理可得高长为8cm,则三角形面积
为48 cm 2.所以长方形的面积也为48cm 2.
设长方形的两边为a和b,那么ab=48,a+b=32÷2=16,
则a=16b,把a=16b代入ab=48,
整理得b216b+48=0,
解得,b1=4,b2=12,
∴a1=12,a2=4.
∴长方形两边分别为12cm和4cm.
(2)底边长为10cm,那么腰长为13cm,由勾股定理可得高长为12cm,则三角形面积为60cm 2.
所以长方形的面积也为60cm2.同样,ab=60,a+b=16,则长方形的两边分别为6cm和10cm.
故选C.
【点评】本题涉及长方形的周长和面积,熟练掌握一元二次方程的解法是关键.
例题2、MN是一面长28m的墙,用长48m的篱笆,围成一个一面是墙,中间隔着一道篱笆的长方形温室大棚ABCD,已知温室大棚的设计面积为180m2,求温室大棚的宽AB应当是多少?
【考点】一元二次方程的应用.
【分析】?设温室大棚的宽为xm,则AB=x,BC=483x,利用面积公式表示出长方形的面积即可列出方程,根据实际情况求出x的值即可.
【解答】设温室大棚的宽为xm,那么它的长是(483x)m 根据题意得方程
x(483x)=180,
即x216x+60=0.
解得x1=6,x2=10,
当x=6时,483x=30>28,
所以x=6(不合题意,舍去).
答:温室大棚的宽为10m.
【点评】考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题的关键是垂直于墙的有三道篱笆.
【夯实基础】
1、老张有一块长65cm,宽60cm的长方形铁皮,准备制作一个工具箱,如图,他将长方形铁皮的四个角各剪掉一个边长xcm的正方形后,剩余的部分刚好能围成一个底面积为Scm2的无盖长方形工具箱,根据题意写出S的函数表达式为( )
A. S=(65x)(60x) B. S=80×704x2
C. S=(802x)(702x) D. S=80×704x2(70+80)x
2、如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了3m,另一边减少了4m,
剩余一块面积为20m2的长方形空地,则原正方形空地的边长是( )
A.7m B.8m C.9m D.10m
3、如图,长方形ABCD的周长是24cm,以AB、AD为边向外作正方形ABEF和正方形
ADGH,若正方形ABEF和ADGH的面积之和为80cm2,那么长方形ABCD的面积是( )
A. 24cm2 B.28cm2 C. 32cm2 D. 36cm2
4、如图,在长为60米,宽为40米的长方形场地上修建1横2纵三条宽度相等的甬道,其余部分为绿地,若绿化面积为长方形面积的一半,则甬道的宽应为多少米?设甬道的宽为x米,则列出的方程不正确的为( )
A.(602x)(40x)=×40×60 B.40×6040×2x60x+2x2=×40×60
C.40×2x+60x2x2=×40×60 D.(60x)(402x)= ×40×60
5、如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,
得到△,若两个三角形重叠部分的面积为4cm2,则它移动的距离等于 .
6、如图,某工厂A距离笔直的公路l为3xkm,与该公路旁的货运中转站D的距离为5xkm. 点
C在线段AD的中垂线上,且BC=4km,则AC= .
7、如图所示,已知甲、乙两人分别从正方形广场ABCD的顶点B、C两点同时出发,甲由C向
D运动,乙由B向C运动,甲的速度为1千米/分,乙的速度为2千米/分,若正方形广场
的周长为80千米,则几分钟后,两人相距10千米?
8、如图,有一段19m米长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用
36m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160m2的长方形场地?
(2)长方形场地面积能达到170m2吗?如果能,
请给出设计方案,如果不能,请说明理由.
【提优特训】
9、如图,将一张正方形铁皮的四个角同时切去边长为3的四个小正方形,制成一个无盖箱子,
若箱子的底面边长为x,原正方形铁皮的面积为2x2+17x,则无盖箱子的外表面积为( )
A.48 B.64 C.72 D.96
10、如图,在宽为24 m、长为36 m的长方形地面上修筑同样宽的道路(图中阴影部分),余下部分作为草坪,要使草坪的面积为693m2,求道路的宽.
A.2 B.3 C.5 D.57
11、在一幅长60cm,宽40cm的长方形风景画的四周镶上一条金色纸边,制成一幅长方形挂图,如果要使整个挂图的面积是3744cm2,设金色纸边的宽为xcm,那么满足的方程是( )
A.x2+50x+336=0 B.x2+50x1344=0 C.x2+50x336=0 D.x2+50x+1344=0
12、已知如图所示的图形的面积为31,根据图中的条件,可列出方程(填一个即可): .
13、为了把一个长100米,宽60米的游泳池扩建成一个周长为600米的大型水上游乐场,把游泳池的长增加x(x>0)米,宽相应增加,那么x等于多少时,水上游乐场的面积为20000平方
米?列车方程? ? ?,解这个方程,得?? ?.
14、已知m是关于x的一元二次方程x211x+1=0的一个根,则m28m+的值 .
15、如图:用同样规格黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形并解答有关问题:
(1)在第n个图中每一横行共有 块瓷砖,每一竖行共有 块瓷砖(均用含n的
代数式表示).
(2)设铺设地面所用瓷砖总数为y,请写出y与(1)中n的函数关系式;并求当y=506时,n的值.
(3) 黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明为什么?
16、如图,在Rt△ACB中,∠C=150°,AC=16cm,BC=12cm,点P、Q同时由A、B两点出发
沿AC、BC向点C匀速移动(当点P到达点C时,点Q同时停止),它们的速度分别是2 cm /秒,
1 cm /秒.
问:(1)写出△PCQ的面积S△PCQ与时间t的函数关系?
(2)几秒后S△PCQ =S△ACB?
17、将一条长为32cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于30cm2吗?若能,求出两段铁丝的长度;若不能,请说
明理由.
(3)则这两个正方形面积之和的最小值是多少cm2.
18、在一块长16m,宽12m的长方形荒地上,要建造一个花园,要求花园所占面积为荒地面积的
一半.下面分别是小明和小颖的设计方案.
小明的设计方案如图1:其中花园四周小路的宽度相等(阴影部分).通过解方程,可得到小路的宽
为2m或12m.
小颖的设计方案如图2:其中花园中每个角上的扇形都相同(阴影部分).
(1)你认为小明的结果对吗?请说明理由;
(2)请你帮助小颖求出图中的x(精确到0.1m);
(3)你还有其他的设计方案吗?请在图3中画出你所设计的草图(标上相关数据).
【中考链接】
19、(2018?广西北海)如图,矩形纸片 ABCD,AB=4,BC=3,点 P 在 BC 边上,将△CDP 沿 DP 折叠,点 C落在点 E 处,PE、DE 分别交 AB 于点 O、F,且 OP=OF,则EF的值为( )
A. B. C.1 D.
20、(2018?大连)8.(3.00分)如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为(? ?)
A.10×64×6x=32? B.(102x)(62x)=32?
C.(10x)(6x)=32 D.10×64x2=32?
21、(2018?山东日照)为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为 .
22、(2018?江苏常州)26.(10.00分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x22x=0,可以通过因式分解把它转化为x(x2+x2)=0,解方程x=0和x2+x2=0,可得方程x3+x22x=0的解.
(1)问题:方程x3+x22x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程=x的解;
(3)应用:如图,已知长方形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
参考答案
1、C 2、B 3、C 4、D 5、2cm 6、 9、B 10、B 11、C 12、x2+x+1=31
13、(100+x)(200x)=20000 ,x=100 14、32 19、A 20、B, 21、x(x+40)=1200
7、如图所示,已知甲、乙两人分别从正方形广场ABCD的顶点B、C两点同时出发,甲由C向
D运动,乙由B向C运动,甲的速度为1千米/分,乙的速度为2千米/分,若正方形广场
的周长为80千米,则几分钟后,两人相距10千米?
解:设x分钟后,两个相距10千米,
则CF=x千米,CE=(202x)千米,
由勾股定理得(0≤x≤10)
x2+(202x)2=102
解得x1=6,x2=10.
当x=6时, CF=6,EC=2012=8<20符合题意
当x=10时,CF=10,EC=2020=0不符合题意,舍去
答:6分钟后,两人相距10千米
8、如图,有一段19m米长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用
36m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160m2的长方形场地?
(2)长方形场地面积能达到170m2吗?如果能,
请给出设计方案,如果不能,请说明理由.
解: (1)设CD=xm,则DE=(362x)m,
依题意得x(362x)=160,
整理得x218x+80=0,
解得x1=10,x2=8,
当x1=10时,362x=16,当x2=8时,362x=20>19(不合题意舍去),
∴能围成一个长16m,宽10m的长方形场地.
(2)设CD=ym,则DE=(362y)m,
依题意得y(362y)=170,整理得y218y+85=0,
△=(18)24×1×85=16<0,故方程没有实数根,
∴长方形场地面积不能达到170m2.
15、如图:用同样规格黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形并解答有关问题:
(1)在第n个图中每一横行共有 块瓷砖,每一竖行共有 块瓷砖(均用含n的
代数式表示).
(2)设铺设地面所用瓷砖总数为y,请写出y与(1)中n的函数关系式;并求当y=506时,n的值.
(3) 黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明为什么?
解:(1)通过观察图形可知,n+3,n+2
(2)当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,①每个图形需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形
数的平方加上图形数;②每个需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等
于图形数的4倍加上6.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为n2+n;
黑瓷砖的块数可用含n的代数式表示为4n+6.
观察图形可知,由题意,得y=(n+3)(n+2)
当y=506时,(n +3)(n+2)=506,
解之,n1 =25(舍去) ,n2 =20.
并求当y=506时, n的值为20块.
在问题(2)中,购买瓷砖共花费:420×3+86×4=1604(元)
(3)每一横行有白砖(n+1)块,每一竖列有白砖n块,因而白砖总数是n(n+1)块,n=20时,需白砖为
20×21=420(块),需黑砖数为86(块).
在问题(2)中,购买瓷砖共花费:420×3+86×4=1604(元).
答:共花1604元钱购买瓷砖.
(4)n(n+1)=4n+6.
解得n= .
因为n不为整数.
∴不存在黑白瓷砖块数相等的情形.
16、如图,在Rt△ACB中,∠C=150°,AC=16cm,BC=12cm,点P、Q同时由A、B两点出发
沿AC、BC向点C匀速移动(当点P到达点C时,点Q同时停止),它们的速度分别是2 cm /秒,
1 cm /秒.
问:(1)写出△PCQ的面积S△PCQ与时间t的函数关系?
(2)几秒后S△PCQ =S△ACB?
解:(1)设t秒后,PC=AC-AP=16-2t,CQ=BCBQ=12t,
∵∠C=150°,
∴∠PCE=180°150°=30°.
∴PE=PC=8t,AD=AC=8.
∴S△PCQ=PE·CQ=(8t)( 12t)=t210t+48.
(2) 设x秒后S△PCQ =S△ACB?
∵△ABC面积为×AD×BC=×8×12=48,
∴x210x+48=×48,
解得x1=4,x2=16(不合题意舍去)
4秒后S△PCQ =S△ACB.
17、将一条长为32cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于30cm2吗?若能,求出两段铁丝的长度;若不能,请说
明理由.
(3)则这两个正方形面积之和的最小值是多少cm2.
解:(1)设其中一个正方形的边长为xcm,则另一个正方形的边长为(8x)cm,
依题意列方程得x2+(8x)2=34,
整理得:x28x+15=0,(x3)(x5)=0,
解方程得x1=3,x2=5,
3×4=12cm,3212=20cm;
或5×4=20cm,3220=12cm.
因此这段铁丝剪成两段后的长度分别是12cm、20cm;
(2)两个正方形的面积之和不可能等于12cm2.
由(1)可知x2+(8x)2=30,
化简后得2x216x+34=0,
∵△=(16)24×2×34=16<0,
∴方程无实数解;
所以两个正方形的面积之和不可能等于30cm2.
(3)设两个正方形的面积和为y,
则y=x2+(8x)2=2(x4)2+32,
∴当x=4时,y的最小值=32,
∴这两个正方形面积之和的最小值是32cm2.
18、在一块长16m,宽12m的长方形荒地上,要建造一个花园,要求花园所占面积为荒地面积的
一半.下面分别是小明和小颖的设计方案.
小明的设计方案如图1:其中花园四周小路的宽度相等(阴影部分).通过解方程,可得到小路的宽
为2m或12m.
小颖的设计方案如图2:其中花园中每个角上的扇形都相同(阴影部分).
(1)你认为小明的结果对吗?请说明理由;
(2)请你帮助小颖求出图中的x(精确到0.1m);
(3)你还有其他的设计方案吗?请在图3中画出你所设计的草图(标上相关数据).
解:(1)小明的结果不对.
设小路宽xm,则得方程(162x)(122x)=×16×12
解得:x1=2,x2=12
而荒地的宽为12m,若小路宽为12m,不符合实际情况,故x2=12m不合题意
(2)由题意得:=×16×12
x2=,x≈5.5m .
答:小颖的设计方案中扇形的半径约为5.5m
(3)
22、(2018?江苏常州)26.(10.00分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x22x=0,可以通过因式分解把它转化为x(x2+x2)=0,解方程x=0和x2+x2=0,可得方程x3+x22x=0的解.
(1)问题:方程x3+x22x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程=x的解;
(3)应用:如图,已知长方形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
【分析】(1)因式分解多项式,然后得结论;
(2)两边平方,把无理方程转化为整式方程,求解,注意验根;
(3)设AP的长为xm,根据勾股定理和BP+CP=10,可列出方程,由于方程含有根号,两边平方,把无理方程转化为整式方程,求解,
【解答】解:(1)x3+x22x=0,
x(x2+x2)=0,
x(x+2)(x1)=0
所以x=0或x+2=0或x1=0
∴x1=0,x2=2,x3=1;
故答案为:2,1;
(2)=x,
方程的两边平方,得2x+3=x2
即x22x3=0
(x3)(x+1)=0
∴x3=0或x+1=0
∴x1=3,x2=1,
当x=1时,==1≠1,
所以1不是原方程的解.
所以方程=x的解是x=3;
(3)因为四边形ABCD是长方形,
所以∠A=∠D=90°,AB=CD=3m
设AP=xm,则PD=(8x)m
因为BP+CP=10,
BP=,CP=
∴=10
∴
两边平方,得(8x)2+9=10020+9+x2
整理,得5=4x+9
两边平方并整理,得x28x+16=0
即(x4)2=0
所以x=4.
经检验,x=4是方程的解.
答:AP的长为4m.
【点评】本题考查了转化的思想方法,一元二次方程的解法.解无理方程是注意到验根.解决(3)时,根据勾股定理和绳长,列出方程是关键.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
