浙江省台州市第三中学2018-2019学年八年级下学期数学第四章 平行四边形单元试卷
文档属性
| 名称 | 浙江省台州市第三中学2018-2019学年八年级下学期数学第四章 平行四边形单元试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 293.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-11 09:02:50 | ||
图片预览



文档简介
第四章 《平行四边形》 单元测试练习
姓名 成绩
一.选择题
1.如图,在?ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO B.AB=CD
C.∠BAD=∠BCD D.AC=BD
2.(2017·辽宁辽阳中考)如图,在?ABCD中,∠BAD=120°,连结BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A.2 B.1 C. D.
3.(2018·四川泸州中考)如图,?ABCD的对角线AC,BD相交于点O,E是AB中点,且AE+EO=4,则?ABCD的周长为( )
A.20 B.16 C.12 D.8
4.如图,A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
A.100° B.110° C.120° D.125°
5.(2018·安徽中考)□ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF
C.AF∥CE D.∠BAE=∠DCF
6. (2018·甘肃兰州中考)如图,矩形ABCD中,AB=3,BC=4,BE∥DF且BE与DF之间的距离为3,则AE的长度是( )
A. B. C. D.
7.(2017·浙江丽水中考)如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A. B.2 C.2 D.4
8.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别为AB,AC,BC的中点,则CD和EF的大小关系是( )
A.CD>EF B.CD<EF
C.CD=EF D.无法比较
9. (2018·江苏苏州中考)如图,在△ABC中,延长BC至D,使得CD=BC.过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD.连结DF,若AB=8,则DF的长为( )
A.3 B.4 C.2 D.3
10.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.DE⊥DC
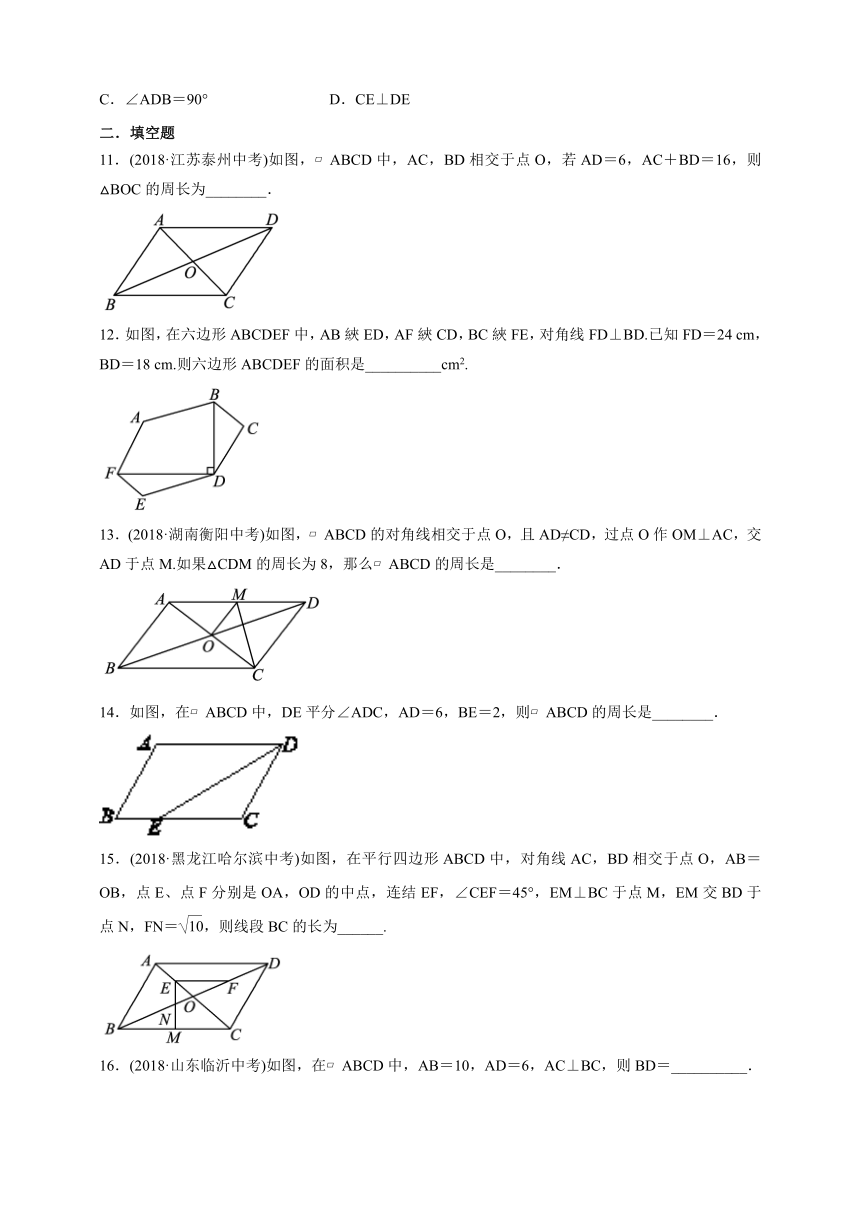
C.∠ADB=90° D.CE⊥DE
二.填空题
11.(2018·江苏泰州中考)如图,?ABCD中,AC,BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为________.
12.如图,在六边形ABCDEF中,AB綊ED,AF綊CD,BC綊FE,对角线FD⊥BD.已知FD=24 cm,BD=18 cm.则六边形ABCDEF的面积是__________cm2.
13.(2018·湖南衡阳中考)如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么?ABCD的周长是________.
14.如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是________.
15.(2018·黑龙江哈尔滨中考)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AB=OB,点E、点F分别是OA,OD的中点,连结EF,∠CEF=45°,EM⊥BC于点M,EM交BD于点N,FN=,则线段BC的长为______.
16.(2018·山东临沂中考)如图,在?ABCD中,AB=10,AD=6,AC⊥BC,则BD=__________.
17.(2018·陕西中考)如图,点O是?ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=AB;G,H分别是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是___________.
18 如图,在?ABCD中,AB=3,BC=5,以点B为圆心,以任意长为半径作弧,分别交BA,BC于点P,Q,再分别以P,Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为________.
三.解答题(共7小题, 66分)
19.(2018·浙江衢州中考)如图,在?ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.
20. 如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8 cm,求线段BE的长.
21.(2019·创新题)阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于点D,交AC于点E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
(1)请回答:BC+DE的值为________.
(2)参考小明思考问题的方法,解决问题:
如图3,已知?ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
22.(2018·云南中考)如图,在平行四边形ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC,平行四边形ABCD的面积为S,由A,E,F三点确定的圆的周长为l.
(1)若△ABE的面积为30,直接写出S的值;
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求l的值.
参考答案
1-5 DBBCB
6-10CCCBB
11. 14
12. 432
13. 16
14. 20
15. 4
16. 4
17. =
18. 2
19. 证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF.又BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.在△ABE与△CDF中,
∴△ABE≌△CDF,∴AE=CF.
20. 解:(1)四边形ACED是平行四边形.理由如下:∵四边形ABCD是正方形,∴AD∥BC.又∵DE∥AC,∴四边形ACED是平行四边形.
(2)由(1)得AD=CE.∵四边形ABCD是正方形,BD=8 cm,易得BC=AD=4 cm,∴BE=BC+CE=2BC=8 cm.
21. 解:(1)
(2)如图,连结AE,CE.∵四边形ABCD是平行四边形,∴AB∥DC.∵四边形ABEF是矩形,∴AB∥FE,BF=AE.∴DC∥FE.∴四边形DCEF是平行四边形.∴CE∥DF.∵AC=BF=DF,∴AC=AE=CE,∴△ACE是等边三角形.∴∠ACE=60°.∵CE∥DF,∴∠AGF=∠ACE=60°.
22. (1)解:如图,作EG⊥AB于点G,则S△ABE=×AB×EG=30,则AB·EG=60,∴平行四边形ABCD的面积为60.
(2)证明:如图,延长AE交BC延长线于点H.∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠ADE=∠HCE,∠DAE=∠CHE.∵E为CD的中点,∴CE=ED,∴△ADE≌△HCE,∴AD=HC,AE=HE,∴AD+FC=HC+FC.由AF=AD+FC和FH=HC+FC得AF=FH,∴∠FAE=∠CHE.又∵∠DAE=∠CHE,∴∠DAE=∠FAE,∴AE平分∠DAF.
(3)解:如图,连结EF.∵AE=BE,AE=HE,∴AE=BE=HE,∴∠BAE=∠ABE,∠HBE=∠BHE.∵∠DAE=∠CHE,∴∠BAE+∠DAE=∠ABE+∠HBE,即∠DAB=∠CBA.由四边形ABCD是平行四边形得∠DAB+∠CBA=180°,∴∠CBA=90°,∴AF2=AB2+BF2=16+(5-FC)2=(FC+CH)2=(FC+5)2,解得FC=,∴AF=FC+CH=.∵AE=HE,AF=FH,∴FE⊥AH,∴AF是△AEF的外接圆直径,∴△AEF的外接圆的周长l=π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
