浙教版八下数学 4.2 夹在两平行线间的平行线段 同步练习(含答案)
文档属性
| 名称 | 浙教版八下数学 4.2 夹在两平行线间的平行线段 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-16 12:25:55 | ||
图片预览




文档简介
浙教版八年级下第四章平行四边形同步练习
4.2 夹在两平行线间的平行线段
题号 一 二 三 总分
得分
第Ⅰ卷(选择题)
评卷人 得 分
一.选择题(共10小题,3*10=30)
1.如图,在△ABC中,DE∥AB,FD∥BC,EF∥CA,则下列说法中错误的是( )
A.AD=EF B.DF=DE C.DF=CE D.AF=DE
2.如图,线段a,b,c的端点分别在直线l1,l2上,则下列说法正确的是( )
A.若l1∥l2,则a=b B.若l1∥l2,则a=c
C.若a∥b,则a=b D.若l1∥l2且a∥b,则a=b
3.如图,AE∥BD,BE∥DF,AB∥CD,下面给出四个结论:①AB=CD;②BE=DF;③S四边形ABDC=S四边形BDFE;④S△ABE=S△CDF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点E是?ABCD边AD上任意一点,且平行四边形的面积为4,则△BCE的面积为( )
A.4 B.3 C.2 D.不能确定,与点E的位置有关
5.如图,AE,CF是?ABCD的两条高,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
6.在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
7.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在方格纸的格点上找一点C,使△ABC的面积为3,则这样的点C共有( )
A.4个 B.5个 C.6个 D.7个
8.如图,点E是?ABCD内的任意一点,若S?ABCD=8,则图中阴影部分的面积是( )
A.3 B.4 C.5 D.6
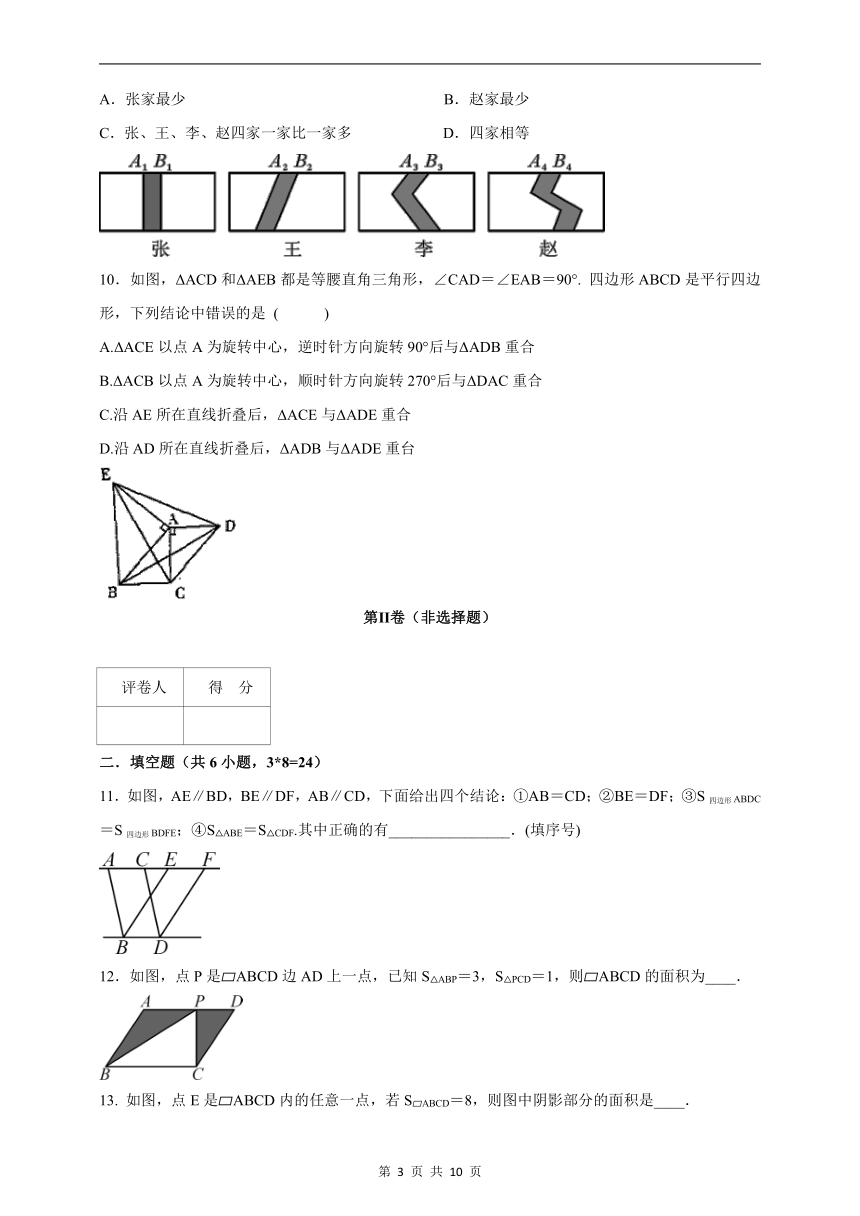
9.如图,张、王、李、赵四家的承包田都是形状、面积完全相同的矩形,四家用不同的方式修路(图中阴影部分),以便施肥、喷药之用,但各家修的路有一个共同特点,即A1B1=A2B2=A3B3=A4B4,且路两侧都是平行的,那么路的占地面积( )
A.张家最少 B.赵家最少
C.张、王、李、赵四家一家比一家多 D.四家相等
10.如图,ΔACD和ΔAEB都是等腰直角三角形,∠CAD=∠EAB=90°. 四边形ABCD是平行四边形,下列结论中错误的是 ( )
A.ΔACE以点A为旋转中心,逆时针方向旋转90°后与ΔADB重合
B.ΔACB以点A为旋转中心,顺时针方向旋转270°后与ΔDAC重合
C.沿AE所在直线折叠后,ΔACE与ΔADE重合
D.沿AD所在直线折叠后,ΔADB与ΔADE重台
第Ⅱ卷(非选择题)
评卷人 得 分
二.填空题(共6小题,3*8=24)
11.如图,AE∥BD,BE∥DF,AB∥CD,下面给出四个结论:①AB=CD;②BE=DF;③S四边形ABDC=S四边形BDFE;④S△ABE=S△CDF.其中正确的有________________.(填序号)
12.如图,点P是?ABCD边AD上一点,已知S△ABP=3,S△PCD=1,则?ABCD的面积为____.
13. 如图,点E是?ABCD内的任意一点,若S?ABCD=8,则图中阴影部分的面积是____.
14.□ABCD中,对角线AC,BD交于点O,EF过点O分别交AB,CD于E,F,那么图中有全等三角形 对.
15如图,在□ABCD中,E在AD上,以BE为折痕把△ABE向上翻折,使点A落在CD上的点F. 若△DEF的周长为8,△FCB的周长为22,则FC= .
16.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,且∠EAF=45°,且AE+AF=2,求□ABCD的周长.
17. 如图,O为□ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=12,则S△DOE的值为 .
18. 如图,□ABCD中,AC⊥AB,∠ABD=30°,AC与BD交于点O,AO=1,则BC的长= ..
评卷人 得 分
三.解答题(共7小题,46分)
19. (6分)如图,在?ABCD中,F,E分别是BA,DC延长线上的点,且AE∥CF,交BC,AD于点G,H.求证:EG=FH.
20.(6分)如图,将?ABCD分成3块,已知图形中阴影部分AEFG是平行四边形,面积是12平方厘米,请分别求出图中三角形ABG和梯形CDEF的面积.
21.(6分)如图,m∥n,AD∥BC,CD∶CF=2∶1,如果△CEF的面积为10,求四边形ABCD的面积.
22. (6分)如图,直线l1∥l2,点A在直线l1上,点B,C在直线l2上,点D是l1上一动点.
(1)写出图中所有面积相等的各组三角形;
(2)当点D在直线l1上运动时(不与点A重合),△BCD的面积是否发生变化?说明理由.
23.(6分)如图,在?ABCD中,AC⊥AB,AB=6,BC=8,
(1)求AB与CD之间的距离;
(2)求AD与BC之间的距离.
24. (8分)如图,把?ABCD分成4个小平行四边形,已知?AEOG,?BFOG,?CFOH的面积分别为8,10,30,求?OEDH的面积.
25. (8分)如图,在平行四边形ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC,平行四边形ABCD的面积为S,由A,E,F三点确定的圆的周长为l.
(1)若△ABE的面积为30,直接写出S的值;
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求l的值.
参考答案
1-5 BDDCC
6-10 CCBDB
11. ①②③④
12. 8
13. 4
14. 6
15. 7
16. 8
17. 1.5
18.
19. 解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∵AB∥CD,AE∥CF,∴AE=CF,∵AD∥BC,
AE∥CF,∴AG=CH,∴AE-AG=CF-CH,即EG=FH
20. 解:分别过点A作AM⊥BC于M,CN⊥AD于N,
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=9 cm,
∴AM=CN,∵S?AEFG=GF·AM,∴AM===4(cm),
∴CN=AM=4 cm,∵四边形AEFG是平行四边形,∴AE=GF=3 cm,
∴DE=6 cm,∴S△ABG=BG·AM=6(cm2),
S梯形CDEF=(CF+DE)·CN=18(cm2)
21. 解:过点A作AG⊥n于点G,EH⊥n于点H,∵m∥n,
∴AG=EH,∵AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,又∵S△CEF=CF·EH=10,CD∶CF=2∶1,
∴S?ABCD=CD·AG=2CF·EH=40
22. 解:(1)面积相等的三角形有:△ABC与△DBC;△ABD与△ACD;△OAB与△OCD
(2)△BCD的面积是不变.理由如下:过点A作AE⊥l2,过点D作DF⊥l2,则AE=DF,∵BC=BC,∴△ABC与△BCD等底等高,∴△BCD的面积是不变的
23. 解:(1)∵四边形ABCD是平行四边形,∴AB∥CD.∵AC⊥AB,∴AC⊥CD,∴AB与CD之间的距离就是AC的长.在Rt△ABC中,AC2=BC2-AB2=82-62=64-36=28,∴AC==2
(2)过点A作AE⊥BC于点E.∵AD∥BC,∴AD与BC之间的距离就是AE的长.由等积法可知AE·BC=AB·AC,∴AE·8=6×2,∴AE==
24. 解:设平行线AD,GH之间的距离为h1,
平行线GH,BC之间的距离为h2,则==
,==,∴=,
即=,∴S?OEDH=24
25. 解:(1)如图,作EG⊥AB于点G,
则S△ABE=×AB×EG=30,则AB·EG=60,
∴平行四边形ABCD的面积为60.
(2)如图,延长AE交BC延长线于点H.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠HCE,∠DAE=∠CHE.
∵E为CD的中点,
∴CE=ED,
∴△ADE≌△HCE,
∴AD=HC,AE=HE,
∴AD+FC=HC+FC.
由AF=AD+FC和FH=HC+FC得AF=FH,
∴∠FAE=∠CHE.
又∵∠DAE=∠CHE,
∴∠DAE=∠FAE,
∴AE平分∠DAF.
(3)如图,连结EF.
∵AE=BE,AE=HE,
∴AE=BE=HE,
∴∠BAE=∠ABE,∠HBE=∠BHE.
∵∠DAE=∠CHE,
∴∠BAE+∠DAE=∠ABE+∠HBE,
即∠DAB=∠CBA.
由四边形ABCD是平行四边形得∠DAB+∠CBA=180°,
∴∠CBA=90°,
∴AF2=AB2+BF2=16+(5-FC)2=(FC+CH)2=(FC+5)2,
解得FC=,
∴AF=FC+CH=.
∵AE=HE,AF=FH,
∴FE⊥AH,
∴AF是△AEF的外接圆直径,
∴△AEF的外接圆的周长l=π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第 1 页 共 3 页
4.2 夹在两平行线间的平行线段
题号 一 二 三 总分
得分
第Ⅰ卷(选择题)
评卷人 得 分
一.选择题(共10小题,3*10=30)
1.如图,在△ABC中,DE∥AB,FD∥BC,EF∥CA,则下列说法中错误的是( )
A.AD=EF B.DF=DE C.DF=CE D.AF=DE
2.如图,线段a,b,c的端点分别在直线l1,l2上,则下列说法正确的是( )
A.若l1∥l2,则a=b B.若l1∥l2,则a=c
C.若a∥b,则a=b D.若l1∥l2且a∥b,则a=b
3.如图,AE∥BD,BE∥DF,AB∥CD,下面给出四个结论:①AB=CD;②BE=DF;③S四边形ABDC=S四边形BDFE;④S△ABE=S△CDF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点E是?ABCD边AD上任意一点,且平行四边形的面积为4,则△BCE的面积为( )
A.4 B.3 C.2 D.不能确定,与点E的位置有关
5.如图,AE,CF是?ABCD的两条高,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
6.在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
7.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在方格纸的格点上找一点C,使△ABC的面积为3,则这样的点C共有( )
A.4个 B.5个 C.6个 D.7个
8.如图,点E是?ABCD内的任意一点,若S?ABCD=8,则图中阴影部分的面积是( )
A.3 B.4 C.5 D.6
9.如图,张、王、李、赵四家的承包田都是形状、面积完全相同的矩形,四家用不同的方式修路(图中阴影部分),以便施肥、喷药之用,但各家修的路有一个共同特点,即A1B1=A2B2=A3B3=A4B4,且路两侧都是平行的,那么路的占地面积( )
A.张家最少 B.赵家最少
C.张、王、李、赵四家一家比一家多 D.四家相等
10.如图,ΔACD和ΔAEB都是等腰直角三角形,∠CAD=∠EAB=90°. 四边形ABCD是平行四边形,下列结论中错误的是 ( )
A.ΔACE以点A为旋转中心,逆时针方向旋转90°后与ΔADB重合
B.ΔACB以点A为旋转中心,顺时针方向旋转270°后与ΔDAC重合
C.沿AE所在直线折叠后,ΔACE与ΔADE重合
D.沿AD所在直线折叠后,ΔADB与ΔADE重台
第Ⅱ卷(非选择题)
评卷人 得 分
二.填空题(共6小题,3*8=24)
11.如图,AE∥BD,BE∥DF,AB∥CD,下面给出四个结论:①AB=CD;②BE=DF;③S四边形ABDC=S四边形BDFE;④S△ABE=S△CDF.其中正确的有________________.(填序号)
12.如图,点P是?ABCD边AD上一点,已知S△ABP=3,S△PCD=1,则?ABCD的面积为____.
13. 如图,点E是?ABCD内的任意一点,若S?ABCD=8,则图中阴影部分的面积是____.
14.□ABCD中,对角线AC,BD交于点O,EF过点O分别交AB,CD于E,F,那么图中有全等三角形 对.
15如图,在□ABCD中,E在AD上,以BE为折痕把△ABE向上翻折,使点A落在CD上的点F. 若△DEF的周长为8,△FCB的周长为22,则FC= .
16.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,且∠EAF=45°,且AE+AF=2,求□ABCD的周长.
17. 如图,O为□ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=12,则S△DOE的值为 .
18. 如图,□ABCD中,AC⊥AB,∠ABD=30°,AC与BD交于点O,AO=1,则BC的长= ..
评卷人 得 分
三.解答题(共7小题,46分)
19. (6分)如图,在?ABCD中,F,E分别是BA,DC延长线上的点,且AE∥CF,交BC,AD于点G,H.求证:EG=FH.
20.(6分)如图,将?ABCD分成3块,已知图形中阴影部分AEFG是平行四边形,面积是12平方厘米,请分别求出图中三角形ABG和梯形CDEF的面积.
21.(6分)如图,m∥n,AD∥BC,CD∶CF=2∶1,如果△CEF的面积为10,求四边形ABCD的面积.
22. (6分)如图,直线l1∥l2,点A在直线l1上,点B,C在直线l2上,点D是l1上一动点.
(1)写出图中所有面积相等的各组三角形;
(2)当点D在直线l1上运动时(不与点A重合),△BCD的面积是否发生变化?说明理由.
23.(6分)如图,在?ABCD中,AC⊥AB,AB=6,BC=8,
(1)求AB与CD之间的距离;
(2)求AD与BC之间的距离.
24. (8分)如图,把?ABCD分成4个小平行四边形,已知?AEOG,?BFOG,?CFOH的面积分别为8,10,30,求?OEDH的面积.
25. (8分)如图,在平行四边形ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC,平行四边形ABCD的面积为S,由A,E,F三点确定的圆的周长为l.
(1)若△ABE的面积为30,直接写出S的值;
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求l的值.
参考答案
1-5 BDDCC
6-10 CCBDB
11. ①②③④
12. 8
13. 4
14. 6
15. 7
16. 8
17. 1.5
18.
19. 解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∵AB∥CD,AE∥CF,∴AE=CF,∵AD∥BC,
AE∥CF,∴AG=CH,∴AE-AG=CF-CH,即EG=FH
20. 解:分别过点A作AM⊥BC于M,CN⊥AD于N,
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=9 cm,
∴AM=CN,∵S?AEFG=GF·AM,∴AM===4(cm),
∴CN=AM=4 cm,∵四边形AEFG是平行四边形,∴AE=GF=3 cm,
∴DE=6 cm,∴S△ABG=BG·AM=6(cm2),
S梯形CDEF=(CF+DE)·CN=18(cm2)
21. 解:过点A作AG⊥n于点G,EH⊥n于点H,∵m∥n,
∴AG=EH,∵AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,又∵S△CEF=CF·EH=10,CD∶CF=2∶1,
∴S?ABCD=CD·AG=2CF·EH=40
22. 解:(1)面积相等的三角形有:△ABC与△DBC;△ABD与△ACD;△OAB与△OCD
(2)△BCD的面积是不变.理由如下:过点A作AE⊥l2,过点D作DF⊥l2,则AE=DF,∵BC=BC,∴△ABC与△BCD等底等高,∴△BCD的面积是不变的
23. 解:(1)∵四边形ABCD是平行四边形,∴AB∥CD.∵AC⊥AB,∴AC⊥CD,∴AB与CD之间的距离就是AC的长.在Rt△ABC中,AC2=BC2-AB2=82-62=64-36=28,∴AC==2
(2)过点A作AE⊥BC于点E.∵AD∥BC,∴AD与BC之间的距离就是AE的长.由等积法可知AE·BC=AB·AC,∴AE·8=6×2,∴AE==
24. 解:设平行线AD,GH之间的距离为h1,
平行线GH,BC之间的距离为h2,则==
,==,∴=,
即=,∴S?OEDH=24
25. 解:(1)如图,作EG⊥AB于点G,
则S△ABE=×AB×EG=30,则AB·EG=60,
∴平行四边形ABCD的面积为60.
(2)如图,延长AE交BC延长线于点H.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠HCE,∠DAE=∠CHE.
∵E为CD的中点,
∴CE=ED,
∴△ADE≌△HCE,
∴AD=HC,AE=HE,
∴AD+FC=HC+FC.
由AF=AD+FC和FH=HC+FC得AF=FH,
∴∠FAE=∠CHE.
又∵∠DAE=∠CHE,
∴∠DAE=∠FAE,
∴AE平分∠DAF.
(3)如图,连结EF.
∵AE=BE,AE=HE,
∴AE=BE=HE,
∴∠BAE=∠ABE,∠HBE=∠BHE.
∵∠DAE=∠CHE,
∴∠BAE+∠DAE=∠ABE+∠HBE,
即∠DAB=∠CBA.
由四边形ABCD是平行四边形得∠DAB+∠CBA=180°,
∴∠CBA=90°,
∴AF2=AB2+BF2=16+(5-FC)2=(FC+CH)2=(FC+5)2,
解得FC=,
∴AF=FC+CH=.
∵AE=HE,AF=FH,
∴FE⊥AH,
∴AF是△AEF的外接圆直径,
∴△AEF的外接圆的周长l=π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第 1 页 共 3 页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
