第三章 数据的分析解答题精选（含解析）

绝密★启用前
第三章数据的分析解答题精选
题号
一
总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上
评卷人
得 分


解答题（共40小题）
1．某食品商店将甲、乙、丙3种糖果的质量按5：4：1配置成一种什锦糖果，已知甲、乙、丙三种糖果的单价分别为16元/kg、20元/kg、27元/kg．若将这种什锦糖果的单价定为这三种糖果单价的算术平均数，你认为合理吗？如果合理，请说明理由；如果不合理，请求出该什锦糖果合理的单价．
2．某校八年级学生开展跳绳比赛活动，每班派5名学生参加，按团体总分多少排列名次，统计发现成绩最好的甲班和乙班总分相等，下表是甲班和乙班学生的比赛数据（单位：个）
选手
1号
2号
3号
4号
5号
总计
甲班
100
98
105
94
103
500
乙班
99
100
95
109
97
500
此时有学生建议，可以通过考察数据中的其他信息作为参考，请解答下列问题：
（1）求两班比赛数据中的中位数，以及方差；
（2）请根据以上数据，说明应该定哪一个班为冠军？为什么？
3．某篮球队在一次联赛中共进行了10场比赛，已知这10场比赛的平均得分为48分，且前9场比赛的得分依次为：57，51，45，51，44，46，45，42，48．
（1）求第10场比赛的得分；
（2）直接写出这10场比赛的中位数，众数和方差．
方差公式：s2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]
4．某校为了分析九年级学生艺术考试的成绩，随机抽查了两个班的各5名学生的成绩，它们分别为：
九（1）班：96，92，94，97，96；
九（2）班：90，98，97，98，92．
通过数据分析，列表如下：
班级
平均分
中位数
众数
九（1）班
95
a
96
九（2）班
95
97
b
（1）a＝　 　，b＝　 　；
（2）计算两个班所抽取的学生艺术成绩的方差，判断哪个班学生的艺术成绩比较稳定．
5．某公司欲招聘一名部门经理，对甲、乙、丙三名候选人进行了三项素质测试．各项测试成绩如表格所示：
测试项目
测试成绩
甲
乙
丙
专业知识
74
87
90
语言能力
58
74
70
综合素质
87
43
50
（1）如果根据三次测试的平均成绩确定人选，那么谁将被录用？
（2）根据实际需要，公司将专业知识、语言能力和综合素质三项测试得分按4：3：1的比例确定每个人的测试总成绩，此时谁将被录用？
（3）请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩，使得乙被录用，若重新设计的比例为x：y：1，且x+y+1＝10，则x＝　 　，y＝　 　．（写出x与y的一组整数值即可）．
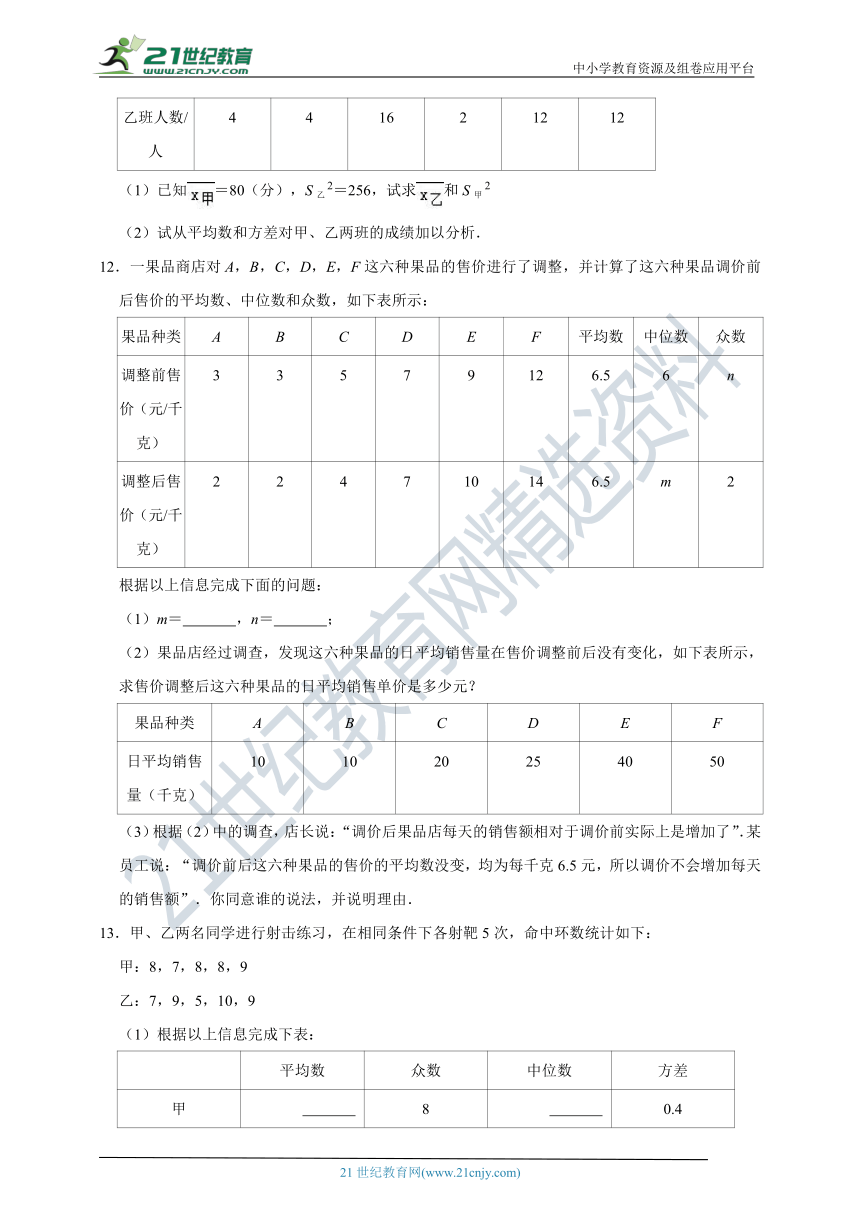
6．某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：
（1）请将下表补充完整：（参考公式：方差S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]）
平均数
方差
中位数
甲
7
　 　
7
乙
　 　
5.4
　 　
（2）请从下列三个不同的角度对这次测试结果进行分析：
①从平均数和方差相结合看，　 　的成绩好些；
②从平均数和中位数相结合看，　 　的成绩好些；
③若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．
7．甲、乙两位同学5次数学成绩统计如表，他们的5次总成绩相同，小明根据他们的成绩绘制了尚不完整的统计图表，请同学们完成下列问题．
第1次
第2次
第3次
第4次
第5次
甲成绩
90
40
70
40
60
乙成绩
70
50
70
a
70
甲、乙两人的数学成绩统计表
（1）a＝　 　，＝　 　；
（2）请完成图中表示乙成绩变化情况的折线；
（3）S甲2＝360，乙成绩的方差是　 　，可看出　 　的成绩比较稳定（填“甲”或“乙”）．从平均数和方差的角度分析，　 　将被选中．
8．为了提高节能意识，深圳某中学对全校的耗电情况进行了统计，他们抽查了10天中全校每天的耗电量，数据如下表：（单位：度）
度数
900
920
950
1010
1050
1100
天数
1
1
2
3
1
2
（1）写出学校这10天耗电量的众数和平均数；
（2）若每度电的定价是0.8元，由上题获得的数据，估计该校每月应付电费是多少？（每月按30天计）
（3）如果做到人走电关，学校每天就可节省电量1%，按照每度电0.8元计算，写出该校节省电费y（元）与天数x（取正整数）之间的函数关系式．
9．甲、乙两名射击队员在相同条件下分别射靶5次，成绩统计如下（单位：环）：
甲
7
8
8
8
9
乙
7
7
7
9
10
（1）分别计算甲、乙两人成绩的平均数；
（2）比较两人的成绩，　 　更稳定（填“甲”或“乙”）；
（3）如果甲、乙两人分别再射击一次，都命中了8环，分别记甲、乙两人6次成绩的方差为S甲2和S乙2，则S甲2　 　S乙2（填“＞”、“＜”、“＝”）．
10．甲、乙两位同学5次数学选拔赛的成绩统计如下表，他们5次考试的总成绩相同，请同学们完成下列问题：
第1 次
第2 次
第 3次
第 4次
第5 次
甲成绩
90
40
70
40
60
乙成绩
70
50
70
a
70
（1）统计表中，a＝　 　，甲同学成绩的中位数为　 　；
（2）小颖计算了甲同学的成绩平均数为60，
方差是S甲2＝[（90﹣60）2+（40﹣60）2+（70﹣60）2+（40﹣60）2+（60﹣60）2]＝360
请你求出乙同学成绩的平均数和方差；
（3）根据统计表及（2）中的结果，请你对甲、乙两位同学的成绩进行分析评价（写出一条意见即可）．
11．在一次科技知识竞赛中，甲、乙两个班学生的成绩统计如下：
分数/分
50
60
70
80
90
100
甲班人数/人
2
5
10
13
14
6
乙班人数/人
4
4
16
2
12
12
（1）已知＝80（分），S乙2＝256，试求和S甲2
（2）试从平均数和方差对甲、乙两班的成绩加以分析．
12．一果品商店对A，B，C，D，E，F这六种果品的售价进行了调整，并计算了这六种果品调价前后售价的平均数、中位数和众数，如下表所示：
果品种类
A
B
C
D
E
F
平均数
中位数
众数
调整前售价（元/千克）
3
3
5
7
9
12
6.5
6
n
调整后售价（元/千克）
2
2
4
7
10
14
6.5
m
2
根据以上信息完成下面的问题：
（1）m＝　 　，n＝　 　；
（2）果品店经过调查，发现这六种果品的日平均销售量在售价调整前后没有变化，如下表所示，求售价调整后这六种果品的日平均销售单价是多少元？
果品种类
A
B
C
D
E
F
日平均销售量（千克）
10
10
20
25
40
50
（3）根据（2）中的调查，店长说：“调价后果品店每天的销售额相对于调价前实际上是增加了”．某员工说：“调价前后这六种果品的售价的平均数没变，均为每千克6.5元，所以调价不会增加每天的销售额”．你同意谁的说法，并说明理由．
13．甲、乙两名同学进行射击练习，在相同条件下各射靶5次，命中环数统计如下：
甲：8，7，8，8，9
乙：7，9，5，10，9
（1）根据以上信息完成下表：
平均数
众数
中位数
方差
甲
　 　
8
　 　
0.4
乙
8
　 　
9
　 　
（2）学校根据这5次成绩，决定选择甲同学参加射击比赛，学校的决定合理吗？为什么？
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差　 　（填“变大”、“变小”或“不变”）
14．为了参加“荆州市中小学生首届诗词大会”，某校八年级的两班学生进行了预选，其中班上前5名学生的成绩（百分制）分别为：八（1）班86，85，77，92，85；八（2）班79，85，92，85，89．通过数据分析，列表如下：
班级
平均分
中位数
众数
方差
八（1）
85
b
c
22.8
八（2）
a
85
85
19.2
（1）直接写出表中a，b，c的值；
（2）根据以上数据分析，你认为哪个班前5名同学的成绩较好？说明理由．
15．甲、乙两人加工同一种直径为100mm的零件，现从它们加工好的零件中随机各抽取6个，量得它们的直径如下（单位：mm）
甲：98，102，100，100，101，99
乙：100，103，101，97，100，99
（1）分别求出上述两组数据的平均数和方差；
（2）结合（1）中的统计数据，请你评价两人的加工质量．
16．甲、乙两名射击运动员进行射击比赛，两人在相同条件下，各射击10次，射击的成绩如图所示．根据统计图信息，整理分析数据如下：
平均成绩（环）
中位数（环）
众数（环）
方差
甲
8
b
8
s2
乙
a
7
c
0.6
（1）补充表格中a，b，c的值，并求甲的方差s2；
（2）运用表中的四个统计量，简要分析这两名运动员的射击成绩，若选派其中一名参赛，你认为应选哪名运动员？
17．从甲、乙两名同学中选拔一人参加“诵读经典”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：
甲：79，86，82，85，83；
乙：88，81，85，81，80．
回答下列问题：
（1）甲成绩的中位数是　 　，乙成绩的众数是　 　；
（2）经计算知乙＝83，S乙2＝．请你求出甲的方差，并运用学过的统计知识推荐参加比赛的合适人选．
18．垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩，测试规则为连续接球10个，每垫球到位1个记1分．
运动员甲测议成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩（分）
7
6
8
7
7
5
8
7
8
7
（1）小明将三人的成绩整理后制作了下面的表格：
平均数
中位数
众数
方差
甲
7
b
7
0.8
乙
7
7
d
0.4
丙
a
c
e
0.81
则表中a＝　 　，b＝　 　，c＝　 　，d＝　 　，e＝　 　．
（2）若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？请作出简要分析．
19．甲乙两组各有10名学生，进行电脑汉字输入速度比赛，现将他们的成绩进行统计，过程如下：
收集数据
各组参赛学生每分钟输入汉字个数统计如表：
输入汉字（个）
132
133
134
135
136
137
甲组人数（人）
1
0
1
5
2
1
乙组人数（人）
0
1
4
1
2
2
分析数据
两组数据的众数、中位数、平均数、方差如下表所示：
组
众数
中位数
平均数（）
方差（s2）
甲组
135
135
135
1.6
乙组
134
134.5
135
1.8
得出结论
（1）若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？
（2）请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）．
20．我市某中学举行十佳歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．
（1）根据所给信息填空：
平均数（分）
中位数（分）
众数（分）
方差
初中部
85
　 　
85
　 　
高中部
　 　
80
　 　
160
（2）你觉得高中部和初中部的决赛成绩哪个更好？说明理由．
21．从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整．
收集数据：
从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染指数（简称：API）的平均值作为每个月的空气污染指数，12个月的空气污染指数如下：
千家店镇：120 115 100 100 95 85 80 70 50 50 50 45
永宁镇：110 90 105 80 90 85 90 60 90 45 70 60
整理、描述数据：
空气质量
按如表整理、描述这两镇空气污染指数的数据：
空气质量为优
空气质量为良
空气质量为轻微污染
千家店镇
4
6
2
永宁镇
　 　
　 　
　 　
（说明：空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．）
分析数据：
两镇的空气污染指数的平均数、中位数、众数如下表所示；
城镇
平均数
中位数
众数
千家店
80
　 　
50
永宁
81.3
87.5
　 　
请将以上两个表格补充完整；
得出结论：可以推断出　 　镇这一年中环境状况比较好，理由为　 　．（至少从两个不同的角度说明推断的合理性）
22．某商场今年8～12月A、B两种品牌的冰箱的销售情况如下表（单位：台）：
品牌
8月
9月
10月
11月
12月
A
13
14
15
16
17
B
10
14
15
16
20
通过整理，得到数据分析表如下：
品牌
平均数（台）
中位数（台）
方差（台2）
A
15
b
2
B
a
15
c
（1）求出表中a、b、c的值；
（2）比较该商场8～12月这两种品牌冰箱月销售量的稳定性．
23．某射击队教练为了了解队员训练情况，从队员中选取甲、乙两名队员进行射击测试，相同条件下各射靶5次，成绩统计如下：
命中环数
6
7
8
9
10
甲命中相应环数的次数
0
1
3
1
0
乙命中相应环数的次数
2
0
0
2
1
（1）根据上述信息可知：甲命中环数的中位数是　 　环，乙命中环数的众数是　 　环；
（2）试通过计算说明甲、乙两人的成绩谁比较稳定？
（3）如果乙再射击1次，命中8环，那么乙射击成绩的方差会　 　．（填“变大”、“变小”或“不变”）
24．射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
（1）完成表中填空①　 　；②　 　；
（2）请计算甲六次测试成绩的方差；
（3）若乙六次测试成绩的方差为，你认为推荐谁参加比赛更合适，请说明理由．
（注：方差公式s2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]）
25．我市某中学举行“中国梦?校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
平均分（分）
中位数（分）
众数（分）
初中部
　 　
85
　 　
高中部
85
　 　
100
（1）根据图示填写表；
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
（3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．
26．某校初三学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：
1号
2号
3号
4号
5号
总数
甲班
100
98
110
89
103
500
乙班
89
100
95
119
97
500
经统计发现两班总数相等．此时有学生建议，可以通过考察数据中的其他信息作为参考．
请你回答下列问题：
（1）填空：甲班的优秀率为　 　，乙班的优秀率为　 　；
（2）填空：甲班比赛数据的中位数为　 　，乙班比赛数据的中位数为　 　；
（3）填空：估计两班比赛数据的方差较小的是　 　班（填甲或乙）
（4）根据以上三条信息，你认为应该把冠军奖状发给哪一个班级？简述你的理由．
27．小明小华和参加学校某种体育项目训练，他们测试成绩如下表1：
测试顺序
1
2
3
4
5
6
7
8
小明
16
14
10
10
11
10
16
17
小华
11
13
13
12
15
13
15
12
根据表一中提供的数据填写表二
表2
平均数
众数
中位数
方差
小明
　 　
10
　 　
8.25
小华
13
　 　
13
　 　
28．甲乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9； 乙：5，9，7，10，9．
（1）填写表格：
平均数　
众数　
中位数　
方差　
　甲
　8
　 　
　8
　0.4
　乙
　 　
9
　 　
　3.2
（2）根据这5次成绩，教练应选择　 　参加射击比赛．
（3）如果乙再射击一次，命中8环，请计算现在乙射击成绩的方差．
29．甲、乙两名队员在相同条件下7次射击的成绩如图所示：
根据以上信息，整理分析数据如下：

平均成绩/环
中位数/环
众数/环
方差/环2
甲
9
②　 　
9
③　 　
乙
①　 　
9
10

（1）完成表格填空；
（2）若选派其中一名参赛，你认为应选哪名队员，并说明理由．
30．某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩计算了甲成绩的平均数和方差（见小宇的作业）．
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7
（1）求a和乙的方差S乙；
（2）请你从平均数和方差的角度分析，谁将被选中．
31．某中学举行演讲比赛，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班所选出的5名选手的复赛成绩（满分为100分）如图所示．
（1）根据上图填写下表：
平均分（分）
中位数（分）
众数（分）
方差
九（1）
85
　 　
85
70
九（2）
85
80
　 　
　 　
（2）结合两班的复赛成绩分析哪个班级的复赛成绩较好．
32．市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
（1）根据表格中的数据，分别计算甲、乙的平均成绩．
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
33．甲、乙两个射击队各有5名队员，在一次选拔练习中，每名队员各打一发子弹，命中环数如下：甲队：9、8、7、7、9；乙队：10、8、9、7、6．
（1）甲乙两队的平均成绩分别为　 　；
（2）甲队成绩的众数为　 　；乙队成绩的中位数为　 　；
（3）甲、乙两队成绩的方差分别为　 　；
（4）①若计划从甲乙两队中选择1对参加团体比赛，你建议选择哪个队？并说明理由：
②若为了取得个人最好成绩，应从哪个队选队员，说明理由．
34．某中学举行“校园?朗读者”朗诵大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
（1）根据图示填写表格；
（2）结合两队成绩的平均数和中位数，　 　队的决赛成绩较好；
（3）已知高中代表队决赛成绩的方差为160，计算初中代表队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．（方差公式：S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]
平均分（分）
中位数（分）
众数（分）
初中部
　 　
85
　 　
高中部
85
　 　
100
35．现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿，两家鸡腿的价格相同，品质相近．快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿．检查人员从两家的鸡腿中各随机抽取15个，记录它们的质量（单位：g）如表所示．
质量（g）
73
74
75
76
77
78
甲的数量
2
4
4
3
1
1
乙的数量
2
3
6
2
1
1
根据表中数据，回答下列问题：
（1）甲厂抽取质量的中位数是　 　g；乙厂抽取质量的众数是　 　g．
（2）如果快餐公司决定从平均数和方差两方面考虑选购，现已知抽取乙厂的样本平均数乙＝75，方差S乙2≈1.86．请你帮助计算出抽取甲厂的样本平均数及方差（结果保留小数点后两位），并指出快餐公司应选购哪家加工厂的鸡腿？
36．为贯彻落实习近平总书记关于弘扬中华优秀传统文化的指示精神，进一步发挥“中国汉字听写大会”和“中国诗词大会”在传承弘扬优秀传统文化中的品牌辐射作用，提升我市中学生的传统文化素养，为参加省赛、国赛做好准备，2017年拟继续举办扬州市中学生汉字听写、诗词诵写大赛．宝应县和高邮市经过初赛、复赛，各选出5名选手组成宝应代表队和高邮代表队参加市7月份的决赛．两个队各选出的5名选手的复赛成绩如图所示．
（1）根据图示填写下表；
平均数（分）
中位数（分）
众数（分）
宝应
83
85
　 　
高邮
　 　
　 　
95
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
37．中国经济的快速发展让众多国家感受到了威胁，随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生，国家安全一再受到威胁，所谓“国家兴亡，匹夫有责”，某校积极开展国防知识教育，九年级甲、乙两班分别选5名同学参加“国防知识”比赛，其预赛成绩如图所示：
（1）根据上图填写下表：

平均数
中位数
众数
方差
甲班
8.5
8.5
　 　
　 　
乙班
8.5
　 　
10
1.6
（2）根据上表数据，分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好．
38．某校初三学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀．表是甲班和乙班成绩最好的5名学生的比赛成绩．
1号
2号
3号
4号
5号
总数
甲班
100
98
102
97
103
500
乙班
99
100
95
109
97
500
经统计发现两班5名学生踢毽子的总个数相等．此时有学生建议，可以通过考查数据中的其它信息作为参考．请你回答下列问题：
（1）甲班的优秀率为60%，则乙班的优秀率为　 　；
（2）甲班比赛成绩的方差S甲2＝，求乙班比赛成绩的方差；
（3）根据以上信息，你认为应该把团体第一名的奖状给哪一个班？简述理由．
39．某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：
1号
2号
3号
4号
5号
总数
甲班
89
100
96
118
97
500
乙班
100
95
110
91
104
500
经统计发现两班总数相等．此时有学生建议，可以通过考察数据中的其他信息作为参考．
请你回答下列问题：
（1）计算两班的优秀率．
（2）计算两班比赛数据的方差．
（3）根据以上信息，你认为应该把冠军奖杯发给哪一个班级？简述你的理由．
40．某校九年级两个班，各选派10名学生参加学校举行的“汉字听写”大赛预赛，各参赛选手的成绩如下：
A班：88，91，92，93，93，93，94，98，98，100
B班：89，93，93，93，95，96，96，98，98，99
通过整理，得到数据分析表如下：
班级
最高分
平均分
中位数
众数
方差
A班
100
a
93
93
c
B班
99
95
b
93
8.4
（1）直接写出表中a、b、c的值；
（2）依据数据分析表，有人说：“最高分在A班，A班的成绩比B班好”，但也有人说B班的成绩要好，请给出两条支持B班成绩好的理由．

参考答案与试题解析
一．解答题（共40小题）
1．某食品商店将甲、乙、丙3种糖果的质量按5：4：1配置成一种什锦糖果，已知甲、乙、丙三种糖果的单价分别为16元/kg、20元/kg、27元/kg．若将这种什锦糖果的单价定为这三种糖果单价的算术平均数，你认为合理吗？如果合理，请说明理由；如果不合理，请求出该什锦糖果合理的单价．
【分析】根据加权平均数的概念进行解答即可．
【解答】解：这样定价不合理，理由如下：
加权平均数：＝16×+20×+27×
＝18.7（元/kg）．
算术平均数＝＝21（元/kg），
21＞18.7，
∴将这种什锦糖果的单价定为这三种糖果单价的算术平均数不合理，
答：该什锦糖果合理的单价为18.7元/kg．
【点评】本题考查了加权平均数的计算公式，熟知加权平均数的概念，正确列出算式是解题的关键．
2．某校八年级学生开展跳绳比赛活动，每班派5名学生参加，按团体总分多少排列名次，统计发现成绩最好的甲班和乙班总分相等，下表是甲班和乙班学生的比赛数据（单位：个）
选手
1号
2号
3号
4号
5号
总计
甲班
100
98
105
94
103
500
乙班
99
100
95
109
97
500
此时有学生建议，可以通过考察数据中的其他信息作为参考，请解答下列问题：
（1）求两班比赛数据中的中位数，以及方差；
（2）请根据以上数据，说明应该定哪一个班为冠军？为什么？
【分析】（1）根据中位数的定义和方差公式分别进行解答即可；
（2）在平均数相同的情形下，利用方差，方差越小成绩越稳定，确定冠军．
【解答】解：（1）把甲班的成绩从小到大排列为：94，98，100，103，105，则甲班的中位数为100，
把乙班的成绩从小到大排列为：95，97，99，100，109，则乙班的中位数为99；
甲班的平均数是：（94+98+100+103+105）＝100（分），
S2甲＝[（94﹣100）2+（98﹣100）2+（100﹣100）2+（103﹣100）2+（105﹣100）2]＝14.8
乙班的平均数是：（95+97+99+100+109）＝100（分），
S2乙＝[（95﹣100）2+（97﹣100）2+（99﹣100）2+（100﹣100）2+（109﹣100）2]＝23.2；
（2）从方差看，甲班成绩稳定，甲为冠军．
【点评】本题考查方差、中位数、平均数等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
3．某篮球队在一次联赛中共进行了10场比赛，已知这10场比赛的平均得分为48分，且前9场比赛的得分依次为：57，51，45，51，44，46，45，42，48．
（1）求第10场比赛的得分；
（2）直接写出这10场比赛的中位数，众数和方差．
方差公式：s2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]
【分析】（1）根据平均数的定义先求出总数，再分别减去前9个数即可；
（2）根据中位数、众数的定义分别求出最中间两个数的平均数和出现次数最多数，再根据方差的计算公式代入计算即可．
【解答】解：（1）∵10场比赛的平均得分为48分，
∴第10场比赛的得分＝48×10﹣57﹣51﹣45﹣41﹣44﹣46﹣45﹣42﹣48＝51（分），
（2）把这10个数从小到大排列为；42、44、45、45、84、48、48、51、51、57，
最中间两个数的平均数是（46+48）÷2＝47，
则这10场比赛得分的中位数为47分，
∵51都出现了最多次数3次，所以众数为51，
方差＝[（42﹣48）2+（44﹣48）2+2×（45﹣48）2+（46﹣48）2+（48﹣48）2+3×（51﹣48）2+（57﹣48）2]＝18.2
【点评】此题考查了平均数、众数与中位数和方差．将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）叫做这组数据的中位数；众数是一组数据中出现次数最多的数；方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
4．某校为了分析九年级学生艺术考试的成绩，随机抽查了两个班的各5名学生的成绩，它们分别为：
九（1）班：96，92，94，97，96；
九（2）班：90，98，97，98，92．
通过数据分析，列表如下：
班级
平均分
中位数
众数
九（1）班
95
a
96
九（2）班
95
97
b
（1）a＝　96　，b＝　98　；
（2）计算两个班所抽取的学生艺术成绩的方差，判断哪个班学生的艺术成绩比较稳定．
【分析】（1）根据中位数和众数的定义求解可得；
（2）根据方差公式计算，再依据方差越小成绩越稳定可得答案．
【解答】解：（1）九（1）班成绩重新排列为92，94，96，96，97，
则中位数a＝96，
九（2）班成绩的众数为b＝98；
故答案为：96，98；
（2）S2（1）班＝×[（96﹣95）2+（92﹣95）2+（94﹣95）2+（97﹣95）2+（96﹣95）2]＝3.2，
S2（2）班＝×[（90﹣95）2+（98﹣95）2+（97﹣95）2+（98﹣95）2+（92﹣95）2]＝11.2，
∵S2（1）班＜S2（2）班，
∴九（1）班学生的艺术成绩比较稳定．
【点评】本题考查了中位数、众数和方差的意义即运用．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
5．某公司欲招聘一名部门经理，对甲、乙、丙三名候选人进行了三项素质测试．各项测试成绩如表格所示：
测试项目
测试成绩
甲
乙
丙
专业知识
74
87
90
语言能力
58
74
70
综合素质
87
43
50
（1）如果根据三次测试的平均成绩确定人选，那么谁将被录用？
（2）根据实际需要，公司将专业知识、语言能力和综合素质三项测试得分按4：3：1的比例确定每个人的测试总成绩，此时谁将被录用？
（3）请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩，使得乙被录用，若重新设计的比例为x：y：1，且x+y+1＝10，则x＝　1　，y＝　8　．（写出x与y的一组整数值即可）．
【分析】（1）运用求平均数公式即可求出三人的平均成绩，比较得出结果；
（2）将三人的总成绩按比例求出测试成绩，比较得出结果．
（3）根据专业知识、语言能力和综合素质三项测试得分可知，乙的语言能力最好，可将语言能力的比例提高，乙将被录用．
【解答】解：（1），
，
．
∵73＞70＞68，
∴甲将被录用；
（2）综合成绩：4+3+1＝8，
，
，
，
∵77.5＞76.625＞69.625，
∴丙将被录用；
（3）x＝1，y＝8或x＝2，y＝7或x＝3，y＝6或x＝4，y＝5时，乙被录用．（答案不唯一，写对一种即可）
故答案为：1，8．
【点评】本题考查了平均数和加权成绩的计算．平均数等于所有数据的和除以数据的个数．
6．某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：
（1）请将下表补充完整：（参考公式：方差S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]）
平均数
方差
中位数
甲
7
　1.2　
7
乙
　7　
5.4
　7.5　
（2）请从下列三个不同的角度对这次测试结果进行分析：
①从平均数和方差相结合看，　甲　的成绩好些；
②从平均数和中位数相结合看，　乙　的成绩好些；
③若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．
【分析】（1）根据统计表，结合平均数、方差、中位数的定义，即可求出需要填写的内容．
（2）①可分别从平均数和方差两方面着手进行比较；
②可分别从平均数和中位数两方面着手进行比较；
③可从具有培养价值方面说明理由．
【解答】解：（1）甲的方差[（9﹣7）2+（5﹣7）2+4×（7﹣7）2+2×（8﹣7）2+2×（6﹣7）2]＝1.2，
乙的平均数：（2+4+6+8+7+7+8+9+9+10）÷10＝7，
乙的中位数：（7+8）÷2＝7.5，
填表如下：
平均数
方差
中位数
甲
7
1.2
7
乙
7
5.4
7.5
（2）①从平均数和方差相结合看，甲的成绩好些；
②从平均数和中位数相结合看，乙的成绩好些；
③选乙参加．
理由：综合看，甲发挥更稳定，但射击精准度差；乙发挥虽然不稳定，但击中高靶环次数更多，成绩逐步上升，提高潜力大，更具有培养价值，应选乙．
故答案为：（1）1.2，7，7.5；（2）①甲；②乙．
【点评】本题考查了折线统计图和综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键，折线统计图能清楚地看出数据的变化情况．
7．甲、乙两位同学5次数学成绩统计如表，他们的5次总成绩相同，小明根据他们的成绩绘制了尚不完整的统计图表，请同学们完成下列问题．
第1次
第2次
第3次
第4次
第5次
甲成绩
90
40
70
40
60
乙成绩
70
50
70
a
70
甲、乙两人的数学成绩统计表
（1）a＝　40　，＝　60　；
（2）请完成图中表示乙成绩变化情况的折线；
（3）S甲2＝360，乙成绩的方差是　160　，可看出　乙　的成绩比较稳定（填“甲”或“乙”）．从平均数和方差的角度分析，　乙　将被选中．
【分析】（1）根据题意和平均数的计算公式计算即可；
（2）根据求出的a的值，完成图中表示乙成绩变化情况的折线；
（3）根据方差的计算公式计算，根据方差的性质进行判断即可．
【解答】解：（1）∵他们的5次总成绩相同，
∴90+40+70+40+60＝70+50+70+a+70，
解得a＝40，
（70+50+70+40+70）＝60，
故答案为：40；60；
（2）如图所示：
（3）S2乙＝[（70﹣60）2+（50﹣60）2+（70﹣60）2+（40﹣60）2+（70﹣60）2]＝160．
∵S2乙＜S甲2，
∴乙的成绩稳定，
从平均数和方差的角度分析，乙将被选中，
故答案为：160；乙；乙．
【点评】本题考查的是条形统计图、方差的计算和性质，读懂条形统计图、获取正确的信息、掌握方差的计算公式是解题的关键．
8．为了提高节能意识，深圳某中学对全校的耗电情况进行了统计，他们抽查了10天中全校每天的耗电量，数据如下表：（单位：度）
度数
900
920
950
1010
1050
1100
天数
1
1
2
3
1
2
（1）写出学校这10天耗电量的众数和平均数；
（2）若每度电的定价是0.8元，由上题获得的数据，估计该校每月应付电费是多少？（每月按30天计）
（3）如果做到人走电关，学校每天就可节省电量1%，按照每度电0.8元计算，写出该校节省电费y（元）与天数x（取正整数）之间的函数关系式．
【分析】（1）根据众数定义可得这10天耗电量的众数是1010度，平均数是计算出10天的用电量，再除以10可得平均用电量；
（2）利用30天的总用电量乘以0.8元即可；
（3）根据题意可得等量关系：节省电费y＝每天的节余电量×天数x，可的函数关系式．
【解答】解：（1）这10天耗电量的众数是1010度，
平均数：（900+920+950×2+1010×3+1050+1100×2）÷10＝1000（度）；
（2）1000×0.8×30＝24000（元）；
（3）y＝0.8×1000x×1%＝8x．
【点评】此题主要考查了一次函数和众数、平均数，关键是正确理解题意，从表格中获取正确信息．
9．甲、乙两名射击队员在相同条件下分别射靶5次，成绩统计如下（单位：环）：
甲
7
8
8
8
9
乙
7
7
7
9
10
（1）分别计算甲、乙两人成绩的平均数；
（2）比较两人的成绩，　甲　更稳定（填“甲”或“乙”）；
（3）如果甲、乙两人分别再射击一次，都命中了8环，分别记甲、乙两人6次成绩的方差为S甲2和S乙2，则S甲2　＜　S乙2（填“＞”、“＜”、“＝”）．
【分析】（1）根据算术平均数的定义列式计算可得；
（2）根据方差的定义列式计算可得；
（3）计算变化后的方差即可得．
【解答】解：（1）＝＝8（环），＝＝8（环）；
（2）∵＝×[（7﹣8）2+（8﹣8）2×3+（9﹣8）2]＝0.8，＝×[（7﹣8）2×3+（9﹣8）2+（10﹣8）2]＝1.6，
∴＜，
∴比较两人的成绩，甲更稳定，
故答案为：甲；
（3）∵甲、乙两人分别再射击一次，都命中了8环，
∴甲、乙平均成绩任然为8环，
而＝×[（7﹣8）2+（8﹣8）2×4+（9﹣8）2]＝，＝×[（7﹣8）2×3+（8﹣8）2+（9﹣8）2+（10﹣8）2]＝，
∴S甲2＜S乙2，
故答案为：＜．
【点评】本题主要考查方差与平均数，解题的关键是熟练掌握算术平均数和方差的定义．
10．甲、乙两位同学5次数学选拔赛的成绩统计如下表，他们5次考试的总成绩相同，请同学们完成下列问题：
第1 次
第2 次
第 3次
第 4次
第5 次
甲成绩
90
40
70
40
60
乙成绩
70
50
70
a
70
（1）统计表中，a＝　40　，甲同学成绩的中位数为　60分　；
（2）小颖计算了甲同学的成绩平均数为60，
方差是S甲2＝[（90﹣60）2+（40﹣60）2+（70﹣60）2+（40﹣60）2+（60﹣60）2]＝360
请你求出乙同学成绩的平均数和方差；
（3）根据统计表及（2）中的结果，请你对甲、乙两位同学的成绩进行分析评价（写出一条意见即可）．
【分析】（1）由“他们5次考试的总成绩相同”可求得a的值，利用中位数的定义求解可得；
（2）利用方差公式计算出乙的方差，
（3）根据方差的意义判断谁的成绩稳定．
【解答】解：（1）根据题意知a＝（90+40+70+40+60）﹣（70+50+70+70）＝40（分），
甲同学成绩的中位数为60分，
故答案为：40，60分．
（2）∵＝×（70+50+70+40+70）＝60，
∴＝[（60﹣70）2+（60﹣50）2+（60﹣70）2+（60﹣40）2+（60﹣70）2]＝160；
（3）因为S乙2＜S甲2，
所以乙同学的成绩比较稳定．（答案不唯一）
【点评】本题考查了方差：方差公式s2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]（可简单记忆为“方差等于差方的平均数”），方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
11．在一次科技知识竞赛中，甲、乙两个班学生的成绩统计如下：
分数/分
50
60
70
80
90
100
甲班人数/人
2
5
10
13
14
6
乙班人数/人
4
4
16
2
12
12
（1）已知＝80（分），S乙2＝256，试求和S甲2
（2）试从平均数和方差对甲、乙两班的成绩加以分析．
【分析】（1）根据方差和平均数的定义计算可得；
（2）根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
【解答】解：（1）甲组的方差为×[2×（80﹣50）2+5×（80﹣60）2+10×（80﹣70）2+13×（80﹣80）2+14×（90﹣80）2+6×（80﹣100）2]＝80；
乙组的平均分为≈80，
乙组的方差为×[4×（80﹣50）2+4×（80﹣60）2+16×（80﹣70）2+2×（80﹣80）2+12×（90﹣80）2+12×（80﹣100）2]≈256；
（2）甲组的平均分数约等于乙组的平均分数，但甲组的方差小于乙组的方差，
所以甲组的分数更优秀一些．
【点评】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，分数越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，分数越稳定．所以该题为甲组优秀．
12．一果品商店对A，B，C，D，E，F这六种果品的售价进行了调整，并计算了这六种果品调价前后售价的平均数、中位数和众数，如下表所示：
果品种类
A
B
C
D
E
F
平均数
中位数
众数
调整前售价（元/千克）
3
3
5
7
9
12
6.5
6
n
调整后售价（元/千克）
2
2
4
7
10
14
6.5
m
2
根据以上信息完成下面的问题：
（1）m＝　5.5　，n＝　3　；
（2）果品店经过调查，发现这六种果品的日平均销售量在售价调整前后没有变化，如下表所示，求售价调整后这六种果品的日平均销售单价是多少元？
果品种类
A
B
C
D
E
F
日平均销售量（千克）
10
10
20
25
40
50
（3）根据（2）中的调查，店长说：“调价后果品店每天的销售额相对于调价前实际上是增加了”．某员工说：“调价前后这六种果品的售价的平均数没变，均为每千克6.5元，所以调价不会增加每天的销售额”．你同意谁的说法，并说明理由．
【分析】（1）依据中位数以及众数的概念，即可得到m，n的值；
（2）依据售价调整后这六种果品的销售总价除以总销量，即可得到售价调整后这六种果品的日平均销售单价；
（3）求得调价前后的日平均收入，并进行比较，即可得到店长的说法正确．
【解答】解：（1）数据2，2，4，7，10，14的中位数m为：＝5.5；
数据3，3，5，7，9，12的众数n为3；
故答案为：5.5，3；
（2）售价调整后这六种果品的日平均销售单价是：
（2×10+2×10+4×20+7×25+10×40+14×50）÷（10+10+20+25+40+50）＝1395÷155＝9（元/千克）；
（3）同意店长的说法．
理由：调价前的日平均收入为：
3×10+3×10+5×20+7×25+9×40+12×50＝1295（元）；
调价前的日平均收入为：
2×10+2×10+4×20+7×25+10×40+14×50＝1395（元），
∵1395＞1295，
∴店长的说法正确．
【点评】本题主要考查了中位数，众数以及平均数的应用，将一组数据按照从小到大（或从大到小）的顺序排列，如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
13．甲、乙两名同学进行射击练习，在相同条件下各射靶5次，命中环数统计如下：
甲：8，7，8，8，9
乙：7，9，5，10，9
（1）根据以上信息完成下表：
平均数
众数
中位数
方差
甲
　8　
8
　8　
0.4
乙
8
　9　
9
　3.2　
（2）学校根据这5次成绩，决定选择甲同学参加射击比赛，学校的决定合理吗？为什么？
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差　变小　（填“变大”、“变小”或“不变”）
【分析】（1）利用平均数、中位数、众数和方差的计算公式求解；
（2）利用方差的大小比较可判断甲成绩确定，从而选择甲同学参加射击比赛；
（3）根据方差公式进行判断．
【解答】解：（1）甲的平均数＝（8+7+8+8+9）＝8，
甲的中位数为8，
乙的众数为9，
乙的方差＝[（7﹣8）2+（9﹣8）2+（5﹣8）2+（10﹣8）2+（9﹣8）2]＝3.2，
故答案为8，8；9，3.2；
（2）合理．因为甲、乙两同学的平均数相等，而甲的方差较小，发挥比较稳定，
所以选择甲同学参加射击比赛比较合理；
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差 变小．
故答案为变小．
【点评】本题考查了方差：记住方差的计算公式（s2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]．也考查了平均数、中位数和众数．
14．为了参加“荆州市中小学生首届诗词大会”，某校八年级的两班学生进行了预选，其中班上前5名学生的成绩（百分制）分别为：八（1）班86，85，77，92，85；八（2）班79，85，92，85，89．通过数据分析，列表如下：
班级
平均分
中位数
众数
方差
八（1）
85
b
c
22.8
八（2）
a
85
85
19.2
（1）直接写出表中a，b，c的值；
（2）根据以上数据分析，你认为哪个班前5名同学的成绩较好？说明理由．
【分析】（1）根据平均数、中位数、众数的概念解答即可；
（2）根据它们的方差，从而可以解答本题．
【解答】解：（1）a＝，b＝85，c＝85，
（2）∵22.8＞19.2，
∴八（2）班前5名同学的成绩较好，
【点评】本题考查平均数、众数、中位数、方差，解题的关键是明确题意，找出所求问题需要的条件．
15．甲、乙两人加工同一种直径为100mm的零件，现从它们加工好的零件中随机各抽取6个，量得它们的直径如下（单位：mm）
甲：98，102，100，100，101，99
乙：100，103，101，97，100，99
（1）分别求出上述两组数据的平均数和方差；
（2）结合（1）中的统计数据，请你评价两人的加工质量．
【分析】（1）直接利用平均数公式和方差公式计算得出答案；
（2）直接利用（1）中所求结合方差的意义得出答案．
【解答】解：（1）＝（98+102+100+100+101+99）＝100，
＝（100+103+101+97+100+99）＝100，
＝[（98﹣100）2+（102﹣100）2+（100﹣100）2+（100﹣100）2+（101﹣100）2+（99﹣100）2]
＝；
＝[（100﹣100）2+（103﹣100）2+（101﹣100）2+（97﹣100）2+（100﹣100）2+（99﹣100）2]
＝；
（2）平均数都等于标准值，但甲的方差比乙的方差小，所以甲的质量更好．
【点评】此题主要考查了方差以及算术平方根，正确记忆方差公式是解题关键．
16．甲、乙两名射击运动员进行射击比赛，两人在相同条件下，各射击10次，射击的成绩如图所示．根据统计图信息，整理分析数据如下：
平均成绩（环）
中位数（环）
众数（环）
方差
甲
8
b
8
s2
乙
a
7
c
0.6
（1）补充表格中a，b，c的值，并求甲的方差s2；
（2）运用表中的四个统计量，简要分析这两名运动员的射击成绩，若选派其中一名参赛，你认为应选哪名运动员？
【分析】（1）由折线统计图得出具体数据，再根据中位数、众数和平均数的定义求解可得；
（2）根据平均数、众数、中位数及方差的意义求解，只要合理即可．
【解答】解：（1）a＝×（6×2+7×7+9）＝7，b＝8，c＝7，
s2＝×[（9﹣8）2+（10﹣8）2+（8﹣8）2+（7﹣8）2+（6﹣8）2+（8﹣8）2+（8﹣8）2+（10﹣8）2+（6﹣8）2+（8﹣8）2]＝1.8．
（2）∵甲的平均成绩、中位数与众数比乙的都高，
∴应选甲运动员．
【点评】本题考查的是折线统计图和方差、平均数、中位数、众数的综合运用．熟练掌握平均数的计算，理解方差的概念，能够根据计算的数据进行综合分析．
17．从甲、乙两名同学中选拔一人参加“诵读经典”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：
甲：79，86，82，85，83；
乙：88，81，85，81，80．
回答下列问题：
（1）甲成绩的中位数是　83分　，乙成绩的众数是　81分　；
（2）经计算知乙＝83，S乙2＝．请你求出甲的方差，并运用学过的统计知识推荐参加比赛的合适人选．
【分析】（1）根据中位数和众数分别求解可得；
（2）先计算出甲的平均数和方差，再根据方差的意义判别即可得．
【解答】解：（1）甲成绩的中位数是83分，乙成绩的众数是81分，
故答案为：83分、81分；
（2）＝×（79+82+83+85+86）＝83，
∴＝×[（﹣4）2+32+（﹣1）2+22+02]＝6，
∵甲＝乙，S甲2＜S乙2，
∴推荐甲去参加比赛．
【点评】此题主要考查了方差、平均数、众数、中位数等统计量，其中方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
18．垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩，测试规则为连续接球10个，每垫球到位1个记1分．
运动员甲测议成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩（分）
7
6
8
7
7
5
8
7
8
7
（1）小明将三人的成绩整理后制作了下面的表格：
平均数
中位数
众数
方差
甲
7
b
7
0.8
乙
7
7
d
0.4
丙
a
c
e
0.81
则表中a＝　6.3　，b＝　7　，c＝　6　，d＝　7　，e＝　6　．
（2）若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？请作出简要分析．
【分析】（1）观察表格可知甲运动员测试成绩的众数和中位数都是7分；
（2）先根据平均数、中位数与众数得出甲、乙较丙优秀一些，再由S甲2＝0.8、S乙2＝0.4，根据方差越小数据越稳定即可判断．
【解答】解：（1）运动员甲测试成绩按从小到大的顺序排列为：5，6，7，7，7，7，7，8，8，8，所以中位数b＝（7+7）÷2＝7．
运动员乙测试成绩中，数据7出现了5次，次数最多，所以众数d＝7．
运动员丙测试成绩的平均数为a＝（2×5+4×6+3×7+1×8）＝6.3，中位数c＝（6+6）÷2＝6，众数e＝6；
故答案是：6.3，7，6，7，6；
（2）∵甲、乙、丙三人的众数为7；7；6，
甲、乙、丙三人的中位数为7；7；6，
甲、乙、丙三人的平均数为7；7；6.3，
∴甲、乙较丙优秀一些，
∵S甲2＞S乙2，
∴选乙运动员更合适．
【点评】本题考查列表法、条形图、折线图、中位数、众数、平均数、方差等知识，熟练掌握基本概念是解题的关键．
19．甲乙两组各有10名学生，进行电脑汉字输入速度比赛，现将他们的成绩进行统计，过程如下：
收集数据
各组参赛学生每分钟输入汉字个数统计如表：
输入汉字（个）
132
133
134
135
136
137
甲组人数（人）
1
0
1
5
2
1
乙组人数（人）
0
1
4
1
2
2
分析数据
两组数据的众数、中位数、平均数、方差如下表所示：
组
众数
中位数
平均数（）
方差（s2）
甲组
135
135
135
1.6
乙组
134
134.5
135
1.8
得出结论
（1）若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？
（2）请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）．
【分析】（1）根据表中给出的数据，得出甲组优秀的人数有3人，乙组优秀的人数有4人，从而得出乙组成绩更好一些；
（2）从中位数看，甲组每分钟输入135字以上的人数比乙组多；从方差看，S2甲＜S2乙；甲组成绩波动小，比较稳定．
【解答】解：（1）∵每分钟输入汉字个数136及以上的甲组人数有3人，乙组有4人，
∴乙组成绩更好一些；
（2）从中位数看，甲组每分钟输入135字以上的人数比乙组多；
从方差看，S2甲＜S2乙；甲组成绩波动小，比较稳定；
【点评】此题考查了平均数、中位数、众数和方差的定义，从表中得到必要的信息是解题的关键．
20．我市某中学举行十佳歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．
（1）根据所给信息填空：
平均数（分）
中位数（分）
众数（分）
方差
初中部
85
　85　
85
　70　
高中部
　85　
80
　100　
160
（2）你觉得高中部和初中部的决赛成绩哪个更好？说明理由．
【分析】（1）根据成绩表加以计算可补全统计表．根据平均数、众数、中位数、方差的统计意义回答；
（2）根据平均数和中位数的统计意义分析得出即可；
【解答】解：（1）填表如下：
平均数（分）
中位数（分）
众数（分）
方差
初中部
85
85
85
70
高中部
85
80
100
160
（2）答：我觉得初中部的成绩更好，因为初中部和高中部的成绩平均数一样，但是初中部的方差比高中部小，成绩更整齐．
故答案为：85，70，85，100．
【点评】此题主要考查了平均数、众数、中位数的统计意义．找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不止一个；平均数是指在一组数据中所有数据之和再除以数据的个数．
21．从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整．
收集数据：
从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染指数（简称：API）的平均值作为每个月的空气污染指数，12个月的空气污染指数如下：
千家店镇：120 115 100 100 95 85 80 70 50 50 50 45
永宁镇：110 90 105 80 90 85 90 60 90 45 70 60
整理、描述数据：
空气质量
按如表整理、描述这两镇空气污染指数的数据：
空气质量为优
空气质量为良
空气质量为轻微污染
千家店镇
4
6
2
永宁镇
　1　
　9　
　2　
（说明：空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．）
分析数据：
两镇的空气污染指数的平均数、中位数、众数如下表所示；
城镇
平均数
中位数
众数
千家店
80
　82.5　
50
永宁
81.3
87.5
　90　
请将以上两个表格补充完整；
得出结论：可以推断出　千家店　镇这一年中环境状况比较好，理由为　千家店镇空气质量优的天数多于永宁镇，千家店镇的污染指数的平均数小于永宁镇或千家店镇空气污染指数的众数是50，属于空气质量优，而永宁镇空气污染指数的众数是90，属于轻微污染．　．（至少从两个不同的角度说明推断的合理性）
【分析】首先根据空气污染指数的数据及空气优、良和轻度污染的标准，对永宁镇进行分类并填空，根据众数和平均数的定义，计算出千家店镇的中位数和永宁镇的众数；根据表格的平均数、中位数、众数对两个镇的情况作出一个简单的判断即可．
【解答】解：永宁镇空气质量为优的天数是1天；空气质量为良的天数为9天；空气质量为轻微污染的天数为2天；
故答案为：1，9，2
千家店镇：120 115 100 100 95 85 80 70 50 50 50 45，
其中位于中间的两个数是85和80，所以其中位数为＝82.5；
永宁镇的数据中，90出现了四次最多，故其众数为90．
故答案为82.5，90．
千家店镇的环境状况较好．（理由不唯一）
例如：千家店镇空气质量优的天数多于永宁镇，千家店镇的污染指数的平均数小于永宁镇或千家店镇空气污染指数的众数是50，属于空气质量优，而永宁镇空气污染指数的众数是90，属于轻微污染等．
【点评】本题考查的是平均数、众数和中位数的定义．要注意，当所给数据有单位时，所求得的平均数、众数和中位数与原数据的单位相同，不要漏单位．
22．某商场今年8～12月A、B两种品牌的冰箱的销售情况如下表（单位：台）：
品牌
8月
9月
10月
11月
12月
A
13
14
15
16
17
B
10
14
15
16
20
通过整理，得到数据分析表如下：
品牌
平均数（台）
中位数（台）
方差（台2）
A
15
b
2
B
a
15
c
（1）求出表中a、b、c的值；
（2）比较该商场8～12月这两种品牌冰箱月销售量的稳定性．
【分析】（1）把A品牌的销售量由小到大排列，根据中位数的定义求出b的值；根据平均数与方差的计算公式求出a、c的值；
（2）根据方差的意义判断这两种品牌冰箱月销售量的稳定性．
【解答】解：（1）A品牌的销售量由小到大排列为：13，14，15，16，17，A品牌的中位数为15，即b＝15；
B品牌的销售量由小到大排列为：10，14，15，16，20，平均数为＝15，
方差为[（10﹣15）2+（14﹣15）2+（15﹣15）2+（16﹣15）2+[（20﹣15）2]＝10.4，
即a＝15，c＝10.4；
（2）∵10.4＞2，即B品牌的方差＞A品牌的方差，
∴该商场8～12月A种品牌冰箱月销售量较稳定．
【点评】本题考查了平均数，中位数，方差的意义．平均数是指在一组数据中所有数据之和再除以数据的个数．它是反映数据集中趋势的一项指标．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
23．某射击队教练为了了解队员训练情况，从队员中选取甲、乙两名队员进行射击测试，相同条件下各射靶5次，成绩统计如下：
命中环数
6
7
8
9
10
甲命中相应环数的次数
0
1
3
1
0
乙命中相应环数的次数
2
0
0
2
1
（1）根据上述信息可知：甲命中环数的中位数是　8　环，乙命中环数的众数是　6和9　环；
（2）试通过计算说明甲、乙两人的成绩谁比较稳定？
（3）如果乙再射击1次，命中8环，那么乙射击成绩的方差会　变小　．（填“变大”、“变小”或“不变”）
【分析】（1）根据众数、中位数的定义求解即可；
（2）根据平均数的定义先求出甲和乙的平均数，再根据方差公式求出甲和乙的方差，然后进行比较，即可得出答案；
（3）根据方差公式进行求解即可．
【解答】解：（1）把甲命中环数从小到大排列为7，8，8，8，9，最中间的数是8，则中位数是8；
在乙命中环数中，6和9都出现了2次，出现的次数最多，则乙命中环数的众数是6和9；
故答案为：8，6和9；
（2）甲的平均数是：（7+8+8+8+9）÷5＝8，
则甲的方差是：[（7﹣8）2+3（8﹣8）2+（9﹣8）2]＝0.4，
乙的平均数是：（6+6+9+9+10）÷5＝8，
则乙的方差是：[2（6﹣8）2+2（9﹣8）2+（10﹣8）2]＝2.8，
所以甲的成绩比较稳定；
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差变小．
故答案为：变小．
【点评】本题考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．方差通常用s2来表示，计算公式是：s2＝[（x1﹣xˉ）2+（x2﹣xˉ）2+…+（xn﹣xˉ）2]；方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．也考查了算术平均数、中位数和众数．
24．射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
（1）完成表中填空①　9　；②　9　；
（2）请计算甲六次测试成绩的方差；
（3）若乙六次测试成绩的方差为，你认为推荐谁参加比赛更合适，请说明理由．
（注：方差公式s2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]）
【分析】（1）根据中位数的定义先把这组数据从小到大排列，再找出最中间两个数的平均数即可求出①；根据平均数的计算公式即可求出②；
（2）根据方差的计算公式S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，代值计算即可；
（3）根据方差的意义：反映了一组数据的波动大小，方差越大，波动性越大，反之也成立，即可得出答案．
【解答】解：（1）甲的中位数是：＝9；
乙的平均数是：（10+7+10+10+9+8）÷6＝9；
故答案为：9，9；
（2）S甲2＝[（10﹣9）2+（8﹣9）2+（9﹣9）2+（8﹣9）2+（10﹣9）2+（9﹣9）2]＝；
（3）∵＝，S甲2＜S乙2，
∴推荐甲参加比赛合适．
【点评】本题考查方差的定义与意义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
25．我市某中学举行“中国梦?校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
平均分（分）
中位数（分）
众数（分）
初中部
　85　
85
　85　
高中部
85
　80　
100
（1）根据图示填写表；
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
（3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．
【分析】（1）根据条形统计图可以计算出初中部的平均分和众数以及高中部的中位数；
（2）根据表格中的数据，可以结合两队成绩的平均数和中位数，说明哪个队的决赛成绩较好；
（3）根据统计图可以计算它们的方差，从而可以解答本题．
【解答】解：（1）由条形统计图可得，
初中5名选手的平均分是：＝85，众数是85，
高中五名选手的成绩是：70，75，80，100，100，故中位数是80，
故答案为：85，85，80；
（2）由表格可知，初中部与高中部的平均分相同，初中部的中位数高，故初中部决赛成绩较好；
（3）由题意可得，
s2初中＝＝70，
s2高中＝＝160，
∵70＜160，
故初中部代表队选手成绩比较稳定．
【点评】本题考查条形统计图、加权平均数、众数、中位数、方差，解题的关键是明确题意，找出所求问题需要的条件．
26．某校初三学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：
1号
2号
3号
4号
5号
总数
甲班
100
98
110
89
103
500
乙班
89
100
95
119
97
500
经统计发现两班总数相等．此时有学生建议，可以通过考察数据中的其他信息作为参考．
请你回答下列问题：
（1）填空：甲班的优秀率为　60%　，乙班的优秀率为　40%　；
（2）填空：甲班比赛数据的中位数为　100　，乙班比赛数据的中位数为　97　；
（3）填空：估计两班比赛数据的方差较小的是　甲　班（填甲或乙）
（4）根据以上三条信息，你认为应该把冠军奖状发给哪一个班级？简述你的理由．
【分析】（1）根据每人踢100个以上（含100）为优秀和图表给出的数据即可得出甲班和乙班的优秀率；
（2）根据中位数的定义先把数据从小到大排列，再找出最中间的数即可；
（3）先求出甲班和乙班的平均数，再根据方差公式即可得出答案；
（4）根据甲班的优秀率高于乙班，甲班的成绩从中位数看也高于乙班，甲班的方差小于乙班，成绩更稳定，从而得出答案．
【解答】解：（1）甲班的优秀率为：×100%＝60%，乙班的优秀率为×100%＝40%；
（2）把甲班比赛数据从小到大排列为：89，98，100，103，110，最中间的数是100，则甲班比赛数据的中位数为100；
把乙班比赛数据从小到大排列为：89，95，97，100，119，最中间的数是97，则乙班比赛数据的中位数为97；
故答案为：100，97；
（3）甲班的平均数是：（89+98+100+103+110）÷5＝100（个）；
乙班的平均数是：（89+95+97+100+119）÷5＝100（个），
甲的方差是：[（89﹣100）2+（98﹣100）2+（100﹣100）2+（103﹣100）2+（110﹣100）2]＝46.8，
乙的方差是：[（89﹣100）2+（95﹣100）2+（97﹣100）2+（100﹣100）2+（119﹣100）2]＝103.2，
则甲班的方差较小；
故答案为：甲；
（4）甲班，理由：甲班的优秀率高于乙班，甲班的成绩从中位数看也高于乙班，甲班的方差小于乙班，成绩更稳定．
【点评】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
27．小明小华和参加学校某种体育项目训练，他们测试成绩如下表1：
测试顺序
1
2
3
4
5
6
7
8
小明
16
14
10
10
11
10
16
17
小华
11
13
13
12
15
13
15
12
根据表一中提供的数据填写表二
表2
平均数
众数
中位数
方差
小明
　13　
10
　12.5　
8.25
小华
13
　13　
13
　1.75　
【分析】平均数是指在一组数据中所有数据之和再除以数据的个数．一组数据中出现次数最多的数据叫做众数．一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．根据平均数、众数和中位数的定义分别求解即可．
【解答】解：小明的成绩的平均数＝（16+14+10+10+11+10+16+17）＝13；
小华的成绩中13出现的次数最多，故众数为13；
小明的成绩排序后，处于中间的两个数据为11和14，故中位数为（11+14）＝12.5；
小华的成绩的方差为[（13﹣11）2+（13﹣13）2+（13﹣13）2+（13﹣12）2+（13﹣15）2+（13﹣13）2+（13﹣15）2+（13﹣12）2]＝1.75；
填表如下：
平均数
众数
中位数
方差
小明
13
10
12.5
8.25
小华
13
13
13
1.75
【点评】本题考查了平均数，中位数、众数及方差的概念，理解它们的概念是解决本题的关键．解题时注意：将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
28．甲乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9； 乙：5，9，7，10，9．
（1）填写表格：
平均数　
众数　
中位数　
方差　
　甲
　8
　8　
　8
　0.4
　乙
　8　
9
　9　
　3.2
（2）根据这5次成绩，教练应选择　甲　参加射击比赛．
（3）如果乙再射击一次，命中8环，请计算现在乙射击成绩的方差．
【分析】（1）根据众数、平均数和中位数的定义求解；
（2）根据平均数相同的情况下，方差越小，发挥越稳定，即可得出答案；
（3）根据方差公式S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，直接代值计算即可．
【解答】解：（1）甲的众数为8，乙的平均数＝×（5+9+7+10+9）＝8，乙的中位数为9；
故答案为：8，8，9；
（2）因为他们的平均数相等，而甲的方差小，发挥比较稳定，所以选择甲参加射击比赛；
故答案为：甲；
（3）因为乙的平均数是8，如果乙再射击1次，命中8环，那么乙的射击平均数还是8，
所以乙射击成绩的方差是：[（5﹣8）2+（9﹣8）2+（7﹣8）2+（10﹣8）2+（9﹣8）2+（8﹣8）2]＝．
【点评】本题考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．方差通常用s2来表示，计算公式是：s2＝[（x1﹣xˉ）2+（x2﹣xˉ）2+…+（xn﹣xˉ）2]；方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．也考查了算术平均数、中位数和众数．
29．甲、乙两名队员在相同条件下7次射击的成绩如图所示：
根据以上信息，整理分析数据如下：

平均成绩/环
中位数/环
众数/环
方差/环2
甲
9
②　9　
9
③　　
乙
①　9　
9
10

（1）完成表格填空；
（2）若选派其中一名参赛，你认为应选哪名队员，并说明理由．
【分析】（1）依据甲队员的射击成绩排列顺序，即可得到中位数；依据平均数即可得到方差的大小；依据乙队员的射击成绩，即可得到平均数；
（2）依据甲乙两队员的平均成绩相同，甲队员的方差较小，说明甲队员成绩较稳定，应该选甲队员参赛．
【解答】解：（1）∵甲队员的射击成绩排列为：8，8，9，9，9，10，10，
∴中位数为9，
方差为：[（8﹣9）2+（8﹣9）2+（9﹣9）2+（9﹣9）2+（9﹣9）2+（10﹣9）2+（10﹣9）2]＝，
乙队员的射击成绩的平均数为：（10+7+10+10+9+8+9）＝9，
故答案为：9，，9；
（2）∵＝，
∴甲乙两队员的平均成绩相同，
又∵，
∴甲队员的方差较小，说明甲队员成绩较稳定，
∴应该选甲队员参赛．
【点评】本题考查了方差的应用，一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
30．某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩计算了甲成绩的平均数和方差（见小宇的作业）．
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7
（1）求a和乙的方差S乙；
（2）请你从平均数和方差的角度分析，谁将被选中．
【分析】（1）根据总成绩相同可以求得a的值，然后求得平均数，利用方差的公式进行计算即可；
（2）因平均数相同，故谁的方差小谁就更稳定，谁就会被选中．
【解答】解：（1）∵乙＝，
∴a＝4，
S乙＝＝1.6；
（2）因为两人成绩的平均水平（平均数）相同，根据方差得出乙的成绩比甲稳定，
所以乙将被选中．
【点评】本题考查了方差及算术平均数的知识，解决本题的关键是熟记方差的计算公式及意义．
31．某中学举行演讲比赛，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班所选出的5名选手的复赛成绩（满分为100分）如图所示．
（1）根据上图填写下表：
平均分（分）
中位数（分）
众数（分）
方差
九（1）
85
　85　
85
70
九（2）
85
80
　100　
　160　
（2）结合两班的复赛成绩分析哪个班级的复赛成绩较好．
【分析】（1）根据统计图中的具体数据以及中位数、众数和方差的概念分别进行计算即可；
（2）观察数据发现：平均数相同，虽九（1）班的众数较低，但是中位数比九（2）班高，方差比九（2）班小，所以九（1）班的复赛成绩较好．
【解答】解：（1）九（1）班的成绩，按从小到大的顺序排列为75、80、85、85、100，第3个数是85，即九（1）班的中位数是85；
九（2）班的成绩为：70、100、100、75、80，出现次数最多的是100，则九（2）班的成绩的众数是100；
九（2）班成绩的方差是：S2＝[（70﹣85）2+（100﹣85）2+（100﹣85）2+（75﹣85）2+（80﹣85）2]＝160；
填表如下：
平均分（分）
中位数（分）
众数（分）
方差
九（1）
85
85
85
70
九（2）
85
80
100
160
故答案为85，100，160；
（2）∵两班的平均数相同，九（1）班的众数较低，但是中位数比九（2）班高，方差比九（2）班小，
∴九（1）班的复赛成绩较好．
【点评】此题考查了条形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．理解平均数、中位数、众数与方差的概念，并能根据它们的意义解决问题．
32．市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
（1）根据表格中的数据，分别计算甲、乙的平均成绩．
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
【分析】（1）根据图表得出甲、乙每次数据和平均数的计算公式列式计算即可；
（2）根据方差公式求出甲、乙六次测试成绩的方差即可；
（3）根据方差和平均数两者进行分析．
【解答】解：（1）甲的平均成绩是：（10+8+9+8+10+9）÷6＝9，
乙的平均成绩是：（10+7+10+10+9+8）÷6＝9；
（2）甲的方差＝[（10﹣9）2+（8﹣9）2+（9﹣9）2+（8﹣9）2+（10﹣9）2+（9﹣9）2]＝．
乙的方差＝[（10﹣9）2+（7﹣9）2+（10﹣9）2+（10﹣9）2+（9﹣9）2+（8﹣9）2]＝．
（3）推荐甲参加全国比赛更合适，理由如下：
两人的平均成绩相等，说明实力相当；但甲的六次测试成绩的方差比乙小，说明甲发挥较为稳定，故推荐甲参加比赛更合适．
【点评】此题主要考查了平均数的求法以及方差的求法，正确的记忆方差公式是解决问题的关键．
33．甲、乙两个射击队各有5名队员，在一次选拔练习中，每名队员各打一发子弹，命中环数如下：甲队：9、8、7、7、9；乙队：10、8、9、7、6．
（1）甲乙两队的平均成绩分别为　8，8　；
（2）甲队成绩的众数为　，7和9　；乙队成绩的中位数为　8　；
（3）甲、乙两队成绩的方差分别为　0.8，2　；
（4）①若计划从甲乙两队中选择1对参加团体比赛，你建议选择哪个队？并说明理由：
②若为了取得个人最好成绩，应从哪个队选队员，说明理由．
【分析】（1）根据平均数的定义计算即可；
（2）根据众数、中位数的定义计算即可；
（3）根据方差的定义计算即可；
（4））①应该选甲，因为甲乙的平均数相同，甲的方差小，成绩稳定．
②应该选乙，因为乙的最高成绩大于甲的最高成绩．
【解答】解：（1）＝＝8，＝＝8，
故答案为8，8．
（2）甲队成绩的众数为7和9，乙队成绩的中位数为8，
故答案为7和9，8．
（3）甲队成绩的方差＝[（8﹣9）2+（8﹣8）2+（8﹣7）2+（8﹣7）2+（8﹣9）2]＝0.8，
乙队成绩的方差＝[（8﹣10）2+（8﹣8）2+（8﹣9）2+（8﹣7）2+（8﹣6）2]＝2，
故答案为0.8，2
（4）①应该选甲，因为甲乙的平均数相同，甲的方差小，成绩稳定．
②应该选乙，因为乙的最高成绩大于甲的最高成绩．
【点评】本题考查平均数、方差、中位数、众数等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
34．某中学举行“校园?朗读者”朗诵大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
（1）根据图示填写表格；
（2）结合两队成绩的平均数和中位数，　初中　队的决赛成绩较好；
（3）已知高中代表队决赛成绩的方差为160，计算初中代表队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．（方差公式：S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]
平均分（分）
中位数（分）
众数（分）
初中部
　85　
85
　85　
高中部
85
　80　
100
【分析】（1）根据条形统计图可以计算出初中部的平均分和众数以及高中部的中位数；
（2）根据表格中的数据，可以结合两队成绩的平均数和中位数，说明哪个队的决赛成绩较好；
（3）根据统计图可以计算它们的方差，从而可以解答本题．
【解答】解：（1）由条形统计图可得，
初中5名选手的平均分是：＝85，众数是85，
高中五名选手的成绩是：70，75，80，100，100，故中位数是80，
故答案为：85，85，80；
（2）由表格可知，初中部与高中部的平均分相同，初中部的中位数高，故初中部决赛成绩较好；
故答案为：初中；
（3）由题意可得，
s2初中＝[（75﹣85）2+（80﹣85）2+（85﹣85）2+（85﹣85）2+（100﹣85）2＝70，
∵70＜160，
故初中部代表队选手成绩比较稳定．
【点评】本题考查条形统计图、加权平均数、众数、中位数、方差，解题的关键是明确题意，找出所求问题需要的条件．
35．现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿，两家鸡腿的价格相同，品质相近．快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿．检查人员从两家的鸡腿中各随机抽取15个，记录它们的质量（单位：g）如表所示．
质量（g）
73
74
75
76
77
78
甲的数量
2
4
4
3
1
1
乙的数量
2
3
6
2
1
1
根据表中数据，回答下列问题：
（1）甲厂抽取质量的中位数是　75　g；乙厂抽取质量的众数是　75　g．
（2）如果快餐公司决定从平均数和方差两方面考虑选购，现已知抽取乙厂的样本平均数乙＝75，方差S乙2≈1.86．请你帮助计算出抽取甲厂的样本平均数及方差（结果保留小数点后两位），并指出快餐公司应选购哪家加工厂的鸡腿？
【分析】（1）根据众数、中位数定义解答；
（2）根据平均数、方差公式解答．
【解答】解：（1）甲厂处在中间位置的数为第8个，为75克，故甲厂质量中位数为75克；
乙厂75克出现了6次，故乙厂众数为75克．
故答案为：75，75．
（2）＝＝75，
＝×[（73﹣75）2×2+（74﹣75）2×4+（75﹣75）2×4+（76﹣75）2×3+（77﹣75）2×1+（78﹣75）2×1）]≈1.87．
∵＜，
∴快餐公司应选购乙加工厂的鸡腿．
【点评】本题考查了方差、加权平均数、中位数、众数，熟悉计算公式和意义是解题的关键．
36．为贯彻落实习近平总书记关于弘扬中华优秀传统文化的指示精神，进一步发挥“中国汉字听写大会”和“中国诗词大会”在传承弘扬优秀传统文化中的品牌辐射作用，提升我市中学生的传统文化素养，为参加省赛、国赛做好准备，2017年拟继续举办扬州市中学生汉字听写、诗词诵写大赛．宝应县和高邮市经过初赛、复赛，各选出5名选手组成宝应代表队和高邮代表队参加市7月份的决赛．两个队各选出的5名选手的复赛成绩如图所示．
（1）根据图示填写下表；
平均数（分）
中位数（分）
众数（分）
宝应
83
85
　85　
高邮
　83　
　80　
95
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
【分析】（1）根据众数、平均数、中位数定义分别求解可得；
（2）平均数都相同，宝应的中位数高，据此可得；
（3）分别计算两队方差，根据方差的意义解答即可．
【解答】解：（1）宝应队85分出现次数最多，有2次，即众数为85；
高邮队成绩如下：70、75、80、95、95，
则其平均数为＝83，中位数为80，
填写下表：
平均数（分）
中位数（分）
众数（分）
宝应
83
85
85
高邮
83
80
95
（2）宝应的成绩好些．因为两个队的平均数都相同，宝应的中位数高，
所以在平均数相同的情况下中位数高的宝应成绩好些．
（3）∵＝[（75﹣83）2+（80﹣83）2+（85﹣85）2+（85﹣83）2+（90﹣83）2]＝26，
＝[（70﹣83）2+（95﹣83）2+（95﹣83）2+（75﹣83）2+（80﹣83）2]＝106．
因此，宝应代表队选手成绩较为稳定．
【点评】此题主要考查了方差的含义和应用，要熟练掌握，解答此题的关键是要明确：方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
37．中国经济的快速发展让众多国家感受到了威胁，随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生，国家安全一再受到威胁，所谓“国家兴亡，匹夫有责”，某校积极开展国防知识教育，九年级甲、乙两班分别选5名同学参加“国防知识”比赛，其预赛成绩如图所示：
（1）根据上图填写下表：

平均数
中位数
众数
方差
甲班
8.5
8.5
　8.5　
　0.7　
乙班
8.5
　8　
10
1.6
（2）根据上表数据，分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好．
【分析】（1）利用条形统计图，结合众数、方差、中位数的定义分别求出答案；
（2）利用平均数、众数、方差、中位数的定义分析得出答案．
【解答】解：（1）甲的众数为：8.5分，
方差为：[（8.5﹣8.5）2+（7.5﹣8.5）2+（8﹣8.5）2+（8.5﹣8.5）2+（10﹣8.5）2]
＝0.7分，
乙的中位数是：8分；
故答案为：8.5，0.7，8；
（2）从平均数看，两班平均数相同，则甲、乙两班的成绩一样好；
从中位数看，甲班的中位数大，所以甲班的成绩较好；
从众数看，乙班的众数大，所以乙班的成绩较好；
从方差看，甲班的方差小，所以甲班的成绩更稳定．
【点评】此题主要考查了平均数、众数、方差、中位数的定义，正确把握相关定义是解题关键
38．某校初三学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀．表是甲班和乙班成绩最好的5名学生的比赛成绩．
1号
2号
3号
4号
5号
总数
甲班
100
98
102
97
103
500
乙班
99
100
95
109
97
500
经统计发现两班5名学生踢毽子的总个数相等．此时有学生建议，可以通过考查数据中的其它信息作为参考．请你回答下列问题：
（1）甲班的优秀率为60%，则乙班的优秀率为　40%　；
（2）甲班比赛成绩的方差S甲2＝，求乙班比赛成绩的方差；
（3）根据以上信息，你认为应该把团体第一名的奖状给哪一个班？简述理由．
【分析】（1）根据已知数据求出优秀率；
（2）利用方差公式求出方差；
（3）根据方差的性质比较解答即可．
【解答】解：（1）×100%＝40%，
∴乙班的优秀率为40%，
故答案为：40%；
（2）乙班的平均数为：×（99+100+95+109+97）＝100，
乙班的方差为：＝[（99﹣100）2+（100﹣100）2+（95﹣100）2+（109﹣100）2+（97﹣100）2]＝；
（3）应该把团体第一名的奖状给甲班，理由如下：
因为甲班的优秀率比乙班高；甲班的方差比乙班低，比较稳定，综合评定甲班比较好．
【点评】本题考查的是方差的计算和性质，掌握方差的计算公式是解题的关键．
39．某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：
1号
2号
3号
4号
5号
总数
甲班
89
100
96
118
97
500
乙班
100
95
110
91
104
500
经统计发现两班总数相等．此时有学生建议，可以通过考察数据中的其他信息作为参考．
请你回答下列问题：
（1）计算两班的优秀率．
（2）计算两班比赛数据的方差．
（3）根据以上信息，你认为应该把冠军奖杯发给哪一个班级？简述你的理由．
【分析】（1）根据优秀率的公式：优秀人数÷总人数×100%，进行计算即可；
（2）根据方差的计算公式，计算即可；
（3）根据优秀率和方差进行比较即可．
【解答】解：（1）甲班的优秀率：＝0.4＝40%，
乙班的优秀率：＝0.6＝60%；
（2）甲班的平均数＝＝100（个），
甲班的方差＝[（89﹣100）2+（100﹣100）2+（96﹣100）2+（118﹣100）2+（97﹣100）2]＝94；
乙班的平均数＝＝100（个），
乙班的方差＝[（100﹣100）2+（95﹣100）2+（110﹣100）2+（91﹣100）2+（104﹣100）2]＝44.4；
（3）冠军奖杯应发给乙班．因为乙班5名学生的比赛成绩的优秀率比甲班高，方差比甲班小，综合评定乙班踢毽子水平较好．
【点评】本题考查了方差，以及优秀率的概念，并且运用它们的意义解决问题．
40．某校九年级两个班，各选派10名学生参加学校举行的“汉字听写”大赛预赛，各参赛选手的成绩如下：
A班：88，91，92，93，93，93，94，98，98，100
B班：89，93，93，93，95，96，96，98，98，99
通过整理，得到数据分析表如下：
班级
最高分
平均分
中位数
众数
方差
A班
100
a
93
93
c
B班
99
95
b
93
8.4
（1）直接写出表中a、b、c的值；
（2）依据数据分析表，有人说：“最高分在A班，A班的成绩比B班好”，但也有人说B班的成绩要好，请给出两条支持B班成绩好的理由．
【分析】（1）求出A班的平均分确定出a的值，求出A班的方差确定出c的值，求出B班的中位数确定出b的值即可；
（2）分别从平均分，方差，以及中位数方面考虑，写出支持B成绩好的原因．
【解答】解：（1）A班的平均分＝＝94，
A班的方差＝，
B班的中位数为（96+95）÷2＝95.5，
故答案为：a＝94 b＝95.5 c＝12；
（2）①B班平均分高于A班；
②B班的成绩集中在中上游，故支持B班成绩好；
【点评】本题考查了方差的计算，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．要学会分析统计数据，运用统计知识解决问题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/3/15 19:26:09；用户：zhrasce20；邮箱：zhrasce20@163.com；学号：6322261