第三章数据分析初步复习课件(32张PPT)
文档属性
| 名称 | 第三章数据分析初步复习课件(32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 913.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-04 10:24:38 | ||
图片预览








文档简介
(共32张PPT)
第3章 数据分析初步
1. 算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2. 计算公式:
x =
x1+x2+ x3+ ··· + xn
n
3. 算术平均数:是反映一组数据的平均水平
情况的量.
加权平均数:在实际生活中,一组数据中各个数据的重要程度是不同的,所以我们在计算这组数据的平均数的时候往往根据其重要程度,分别给每个数据一个“权”。这样,计算出来的平均数叫做加权平均数。
加权平均数
老师对同学们每学期总评成绩是这样做的: 平时练习占
30%, 期中考试占30%, 期末考试占40%. 某同学平时练习93
分, 期中考试87分, 期末考试95分, 那么如何来评定该同学的
学期总评成绩呢
解:
该同学的学期总评成绩是:
93×30%
=92(分)
+
95×40%
87×30%
+
加权平均数
权 数
权数的意义:
各个数据在该组数据中所占的比例.
加权平均数的意义:
按各个数据的权数大小来反映该组数据的总体平均量
解:先确定这组数据中1.60,1.64,1.68的权数?
例题:有一组数据如下:1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.求出这组数据的
加权平均数.
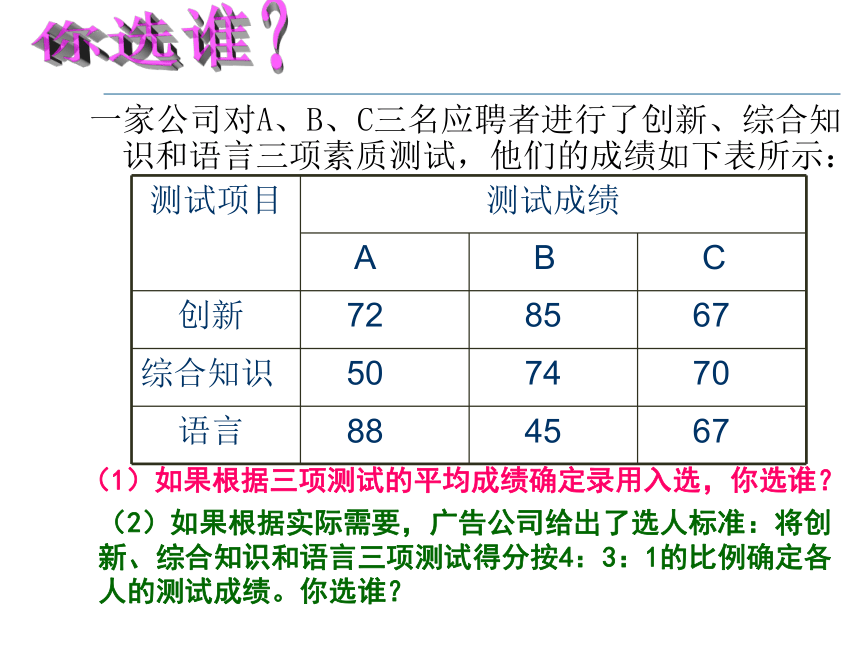
一家公司对A、B、C三名应聘者进行了创新、综合知识和语言三项素质测试,他们的成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(2)如果根据实际需要,广告公司给出了选人标准:将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人的测试成绩。你选谁?
(1)如果根据三项测试的平均成绩确定录用入选,你选谁?
解:(1)A的平均成绩为(72+50+88)/3=70分。
B的平均成绩为(85+74+45)/3=68分。
C的平均成绩为(67+70+67)/3=68分。
由于70>68,故A将被录用。
(2)根据题意,
A的成绩为:72× +50× +88× =65.75分。
B的成绩为:85× +74× +45× =75.875分。
C的成绩为:67× +70× +67× =68.125分。
因此候
选人B将 被录用
由(1)(2)的结果不一样,
说明了:⑴权数的设置直接影响着平均数,
⑵算术平均数实际上给每个数设置的权数是相同的
⑶权数越大这个数对平均数影响越大
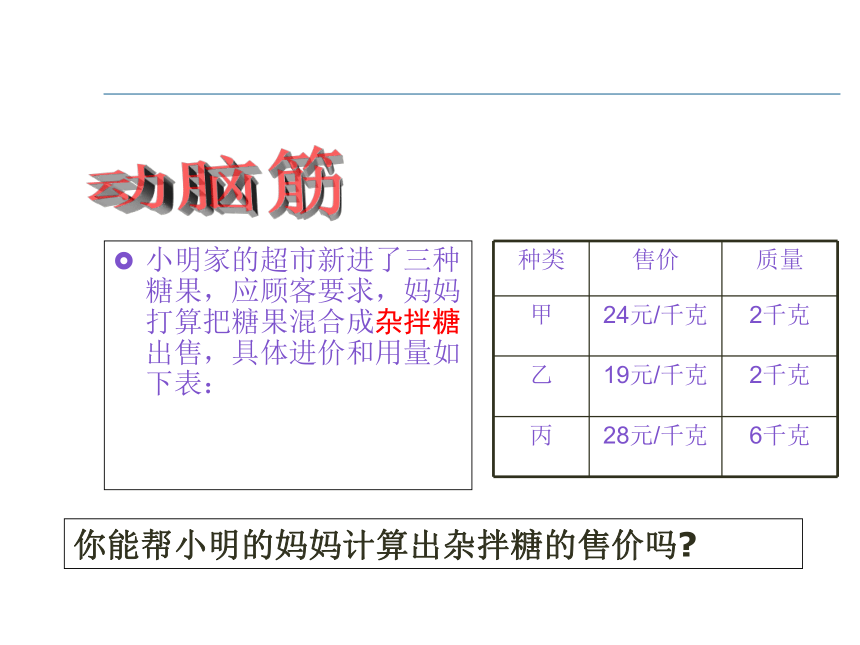
小明家的超市新进了三种糖果,应顾客要求,妈妈打算把糖果混合成杂拌糖出售,具体进价和用量如下表:
种类 售价 质量
甲 24元/千克 2千克
乙 19元/千克 2千克
丙 28元/千克 6千克
你能帮小明的妈妈计算出杂拌糖的售价吗
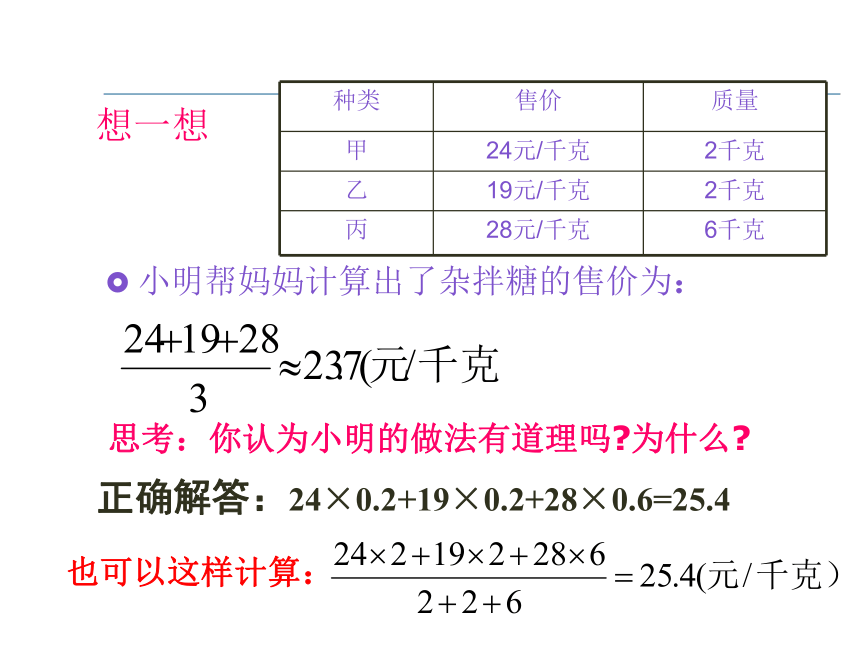
小明帮妈妈计算出了杂拌糖的售价为:
思考:你认为小明的做法有道理吗 为什么
想一想
种类 售价 质量
甲 24元/千克 2千克
乙 19元/千克 2千克
丙 28元/千克 6千克
正确解答:24×0.2+19×0.2+28×0.6=25.4
也可以这样计算:
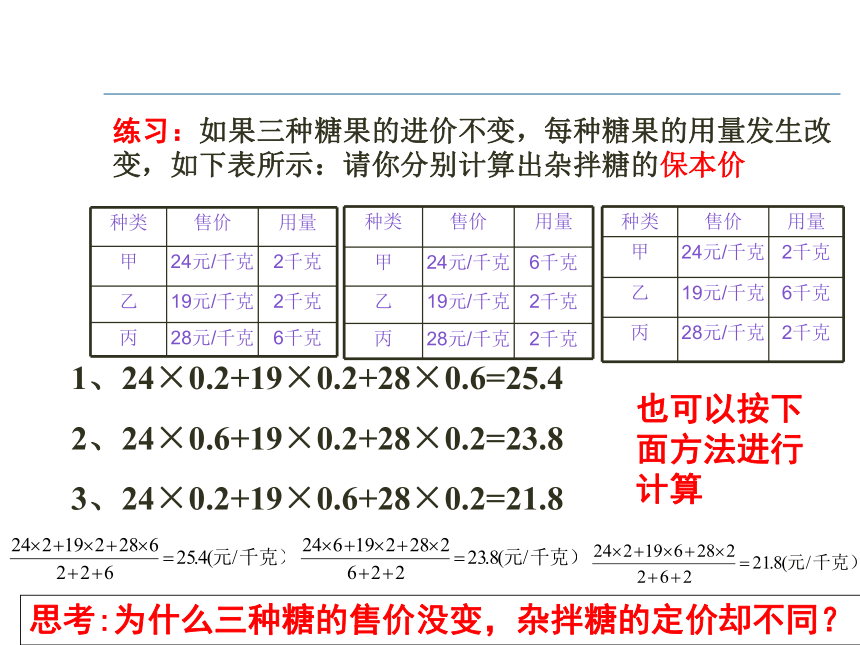
练习:如果三种糖果的进价不变,每种糖果的用量发生改变,如下表所示:请你分别计算出杂拌糖的保本价
种类 售价 用量
甲 24元/千克 2千克
乙 19元/千克 6千克
丙 28元/千克 2千克
种类 售价 用量
甲 24元/千克 6千克
乙 19元/千克 2千克
丙 28元/千克 2千克
思考:为什么三种糖的售价没变,杂拌糖的定价却不同?
种类 售价 用量
甲 24元/千克 2千克
乙 19元/千克 2千克
丙 28元/千克 6千克
1、24×0.2+19×0.2+28×0.6=25.4
2、24×0.6+19×0.2+28×0.2=23.8
3、24×0.2+19×0.6+28×0.2=21.8
也可以按下面方法进行计算
1、一组数据为10,8,9,12,13,10,8,则这组数据的平均数是
2、已知 的平均数为6,则
3、4个数的平均数是6,6个数的平均数是11,则这几个数的平均数是
4、在一次满分制为5分的数学测验中,某班男同学中有10个得5分,5个得4分,4个得 3分,2个得1分,4个得0分,则这个班男生的平均分为
5、园园参加了4门功课的考试,平均成绩是82分,若计划在下一门功课考完后,使5门功课成绩平均分为85分,那么她下一门功课至少应得的分数为
练习题一.
7、已知数据x1,x2,x3的平均数为a,数据y1,y2,y3的平均数为b,则数据3x1+y1,3x2+y2,3x3+y3的平均数为 .
5、有100个数,它们的平均数为78.5,现在将其中的两个数82和26去掉,则现在余下来的数的平均数是____。
6、若3、4、5、6、a、b、c的平均数是12,则a+b+c=____
中位数定义:把一组数据从小到大的顺序排列,位于中间的数称为这组数据的中位数.
⑵如果数据的个数是偶数个时,那么位于中间位置的两个数的平均数称为这组数据的中位数
⑴如果数据的个数是奇数个,那么恰好位于中间的数就是这组数据的中位数.
中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数.
因此,中位数常用来描述“中间位置”或“中等水平”,但中位数没有利用数据组中所有的信息.
例 找出下列两组数据的中位数:
(1)14,11,13,10,17,16,28;
(2)453,442,450,445,446,457,448,449,
451,450
解
先把这组数据从小到大排列:
10,11,13,14,16,17,28
位于中间的数是14,因此这组数据的中位数是14.
中位数
(1)14,11,13,10,17,16,28;
解
把这组数据从小到大排列:
442,445,446,448,449,450,450,451,453,457
位于中间的两个数是449和450,这两个数的平均数是 449.5,因此这组数据的中位数是449.5.
中间的两个数
(2)453,442,450,445,446,457,448,449,
451,450.
练习
1. 求下列各组数据的中位数:
(1)100,75,80,73,50,60,70;
解
把这组数据从小到大排列:
50,60,70,73,75,80,100
位于中间的数是73,因此这组数据的中位数是73.
2. 求下面一组数据的中位数和平均数:
17,12,5,9,5,14;
解
把这组数据从小到大排列:
5,5,9,12,14,17
位于中间的数是9和12,这两个数的平均数是10.5,因此这组数据的中位数是10.5;
这组数据的平均数是:(17+12+5+9+5+14)÷6=10.3
众数的定义:在一组数据中,把出现次数最多的数叫做这组数据的众数众数.(允许一组数据有多个出现)
举例:下面是一家鞋店在一段时间内各种尺码的男鞋的销售情况统计表:
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 13 17 10 8 4
试求出这家鞋店数据中的众数 、中位数 .
25
25
练习
1. 求下列各组数据的众数:
(1)3,4,4,5,3,5,6,5,6;
解
根据题意可知,5出现的次数最多,
因此,5是这组数据的众数.
(2)1.0,1.1,1.0,0.9,0.8,0.9,1.1,0.9
解
根据题意可知,0.9出现的次数最多,因此,0.9是这组数据的众数.
2. 某班30人所穿运动服尺码的情况为:穿75号码的有5人,穿80号码的有6人,穿85号码的有15人,穿90号码的有3人,穿95号码的有1人. 穿哪一种尺码衣服的人最多?这个数据称为什么数?
解
根据题意可知,穿85号衣服的人最多.
因此85号是这组衣服尺码数据的众数.
1.某部队一位新兵连续射靶5次,命中环数如下:
0,2,5,2,7,这组数的中位数是( ).
A.0 B.2 C.5 D.7
2.某篮球队12名队员年龄如下:则这12名队员的中位数是( ).
A.19 B.20 C.21 D.22
年龄(岁) 18 19 20 21 22
人数 1 4 3 2 2
练习题二.
B
B
4.已知数据1、2、x、5的平均数为2.5,则这组数据的中位数与众数分别是____、 ____。
2
2
3.一组数据从小到大排列为-10,-3,0,8,10,15。如果通过增大数据-10来改变该数据的中位数,那么至少使其大于( ).
A.O B.3 C.8 D.10
D
5.某公司有15名员工,他们所在的部门及相应每人所创的年利润如下表所示:
部门 A B C D E F G
人数(个) 1 1 2 4 2 2 3
利润(万元) 20 5 2.5 2.1 1.5 1.5 1.2
⑴.求该公司每人所创年利润的平均数( )万元和中位数( )万元;
⑵.你认为使用平均数和中位数中哪一个来描述
该公司每人所创年利润的一般水平比较合理 ( )
中位数
3.2
2.1
为了反映一组数据的离散程度,可以采用很多方法,统计中常采用以下做法:
方差的定义:设一组数据为x1,x2,…,xn,各数据与 平均数 之差的平方的平均值,叫做这组数据的方差,记做 s2.
即
计算方差的步骤可概括为:
“先平均,后求差,平方后,再平均”.
刘亮和李飞参加射击训练的成绩(单位:环)如下:
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
(1) 两人的平均成绩分别是多少?
(2) 计算这两组数据的方差?
(3) 谁的成绩比较稳定?
刘亮、李飞的射击成绩的方差分别是
计算结果表明: s2李飞> s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
1、已知一组数据为2、0、-1、3、-4,则这组数据的方差为 .
2、甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:甲:7、8、6、8、6、5、9、10、7、4
乙:9、5、7、8、7、6、8、6、7、7
经过计算,两人射击环数的平均数相同,但 S S ,所以确定__去参加比赛。
练习题三.
S2=6
>
乙
3.甲、乙两台机床生产同种零件,10天出的次品分别是
甲:0、1、0、2、2、0、3、1、2、4
乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,
根据你的计算判断哪台机床的性能较好?
4.从甲、乙两种农作物中各抽取10株苗,分别测得它的苗高如下:(单位:cm)
甲:9、10、11、12、7、13、10、8、12、8;
乙:8、13、12、11、10、12、7、7、9、11;
问:(1)哪种农作物的苗长的比较高?
(2)哪种农作物的苗长得比较整齐?
第3章 数据分析初步
1. 算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2. 计算公式:
x =
x1+x2+ x3+ ··· + xn
n
3. 算术平均数:是反映一组数据的平均水平
情况的量.
加权平均数:在实际生活中,一组数据中各个数据的重要程度是不同的,所以我们在计算这组数据的平均数的时候往往根据其重要程度,分别给每个数据一个“权”。这样,计算出来的平均数叫做加权平均数。
加权平均数
老师对同学们每学期总评成绩是这样做的: 平时练习占
30%, 期中考试占30%, 期末考试占40%. 某同学平时练习93
分, 期中考试87分, 期末考试95分, 那么如何来评定该同学的
学期总评成绩呢
解:
该同学的学期总评成绩是:
93×30%
=92(分)
+
95×40%
87×30%
+
加权平均数
权 数
权数的意义:
各个数据在该组数据中所占的比例.
加权平均数的意义:
按各个数据的权数大小来反映该组数据的总体平均量
解:先确定这组数据中1.60,1.64,1.68的权数?
例题:有一组数据如下:1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.求出这组数据的
加权平均数.
一家公司对A、B、C三名应聘者进行了创新、综合知识和语言三项素质测试,他们的成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(2)如果根据实际需要,广告公司给出了选人标准:将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人的测试成绩。你选谁?
(1)如果根据三项测试的平均成绩确定录用入选,你选谁?
解:(1)A的平均成绩为(72+50+88)/3=70分。
B的平均成绩为(85+74+45)/3=68分。
C的平均成绩为(67+70+67)/3=68分。
由于70>68,故A将被录用。
(2)根据题意,
A的成绩为:72× +50× +88× =65.75分。
B的成绩为:85× +74× +45× =75.875分。
C的成绩为:67× +70× +67× =68.125分。
因此候
选人B将 被录用
由(1)(2)的结果不一样,
说明了:⑴权数的设置直接影响着平均数,
⑵算术平均数实际上给每个数设置的权数是相同的
⑶权数越大这个数对平均数影响越大
小明家的超市新进了三种糖果,应顾客要求,妈妈打算把糖果混合成杂拌糖出售,具体进价和用量如下表:
种类 售价 质量
甲 24元/千克 2千克
乙 19元/千克 2千克
丙 28元/千克 6千克
你能帮小明的妈妈计算出杂拌糖的售价吗
小明帮妈妈计算出了杂拌糖的售价为:
思考:你认为小明的做法有道理吗 为什么
想一想
种类 售价 质量
甲 24元/千克 2千克
乙 19元/千克 2千克
丙 28元/千克 6千克
正确解答:24×0.2+19×0.2+28×0.6=25.4
也可以这样计算:
练习:如果三种糖果的进价不变,每种糖果的用量发生改变,如下表所示:请你分别计算出杂拌糖的保本价
种类 售价 用量
甲 24元/千克 2千克
乙 19元/千克 6千克
丙 28元/千克 2千克
种类 售价 用量
甲 24元/千克 6千克
乙 19元/千克 2千克
丙 28元/千克 2千克
思考:为什么三种糖的售价没变,杂拌糖的定价却不同?
种类 售价 用量
甲 24元/千克 2千克
乙 19元/千克 2千克
丙 28元/千克 6千克
1、24×0.2+19×0.2+28×0.6=25.4
2、24×0.6+19×0.2+28×0.2=23.8
3、24×0.2+19×0.6+28×0.2=21.8
也可以按下面方法进行计算
1、一组数据为10,8,9,12,13,10,8,则这组数据的平均数是
2、已知 的平均数为6,则
3、4个数的平均数是6,6个数的平均数是11,则这几个数的平均数是
4、在一次满分制为5分的数学测验中,某班男同学中有10个得5分,5个得4分,4个得 3分,2个得1分,4个得0分,则这个班男生的平均分为
5、园园参加了4门功课的考试,平均成绩是82分,若计划在下一门功课考完后,使5门功课成绩平均分为85分,那么她下一门功课至少应得的分数为
练习题一.
7、已知数据x1,x2,x3的平均数为a,数据y1,y2,y3的平均数为b,则数据3x1+y1,3x2+y2,3x3+y3的平均数为 .
5、有100个数,它们的平均数为78.5,现在将其中的两个数82和26去掉,则现在余下来的数的平均数是____。
6、若3、4、5、6、a、b、c的平均数是12,则a+b+c=____
中位数定义:把一组数据从小到大的顺序排列,位于中间的数称为这组数据的中位数.
⑵如果数据的个数是偶数个时,那么位于中间位置的两个数的平均数称为这组数据的中位数
⑴如果数据的个数是奇数个,那么恰好位于中间的数就是这组数据的中位数.
中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数.
因此,中位数常用来描述“中间位置”或“中等水平”,但中位数没有利用数据组中所有的信息.
例 找出下列两组数据的中位数:
(1)14,11,13,10,17,16,28;
(2)453,442,450,445,446,457,448,449,
451,450
解
先把这组数据从小到大排列:
10,11,13,14,16,17,28
位于中间的数是14,因此这组数据的中位数是14.
中位数
(1)14,11,13,10,17,16,28;
解
把这组数据从小到大排列:
442,445,446,448,449,450,450,451,453,457
位于中间的两个数是449和450,这两个数的平均数是 449.5,因此这组数据的中位数是449.5.
中间的两个数
(2)453,442,450,445,446,457,448,449,
451,450.
练习
1. 求下列各组数据的中位数:
(1)100,75,80,73,50,60,70;
解
把这组数据从小到大排列:
50,60,70,73,75,80,100
位于中间的数是73,因此这组数据的中位数是73.
2. 求下面一组数据的中位数和平均数:
17,12,5,9,5,14;
解
把这组数据从小到大排列:
5,5,9,12,14,17
位于中间的数是9和12,这两个数的平均数是10.5,因此这组数据的中位数是10.5;
这组数据的平均数是:(17+12+5+9+5+14)÷6=10.3
众数的定义:在一组数据中,把出现次数最多的数叫做这组数据的众数众数.(允许一组数据有多个出现)
举例:下面是一家鞋店在一段时间内各种尺码的男鞋的销售情况统计表:
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 13 17 10 8 4
试求出这家鞋店数据中的众数 、中位数 .
25
25
练习
1. 求下列各组数据的众数:
(1)3,4,4,5,3,5,6,5,6;
解
根据题意可知,5出现的次数最多,
因此,5是这组数据的众数.
(2)1.0,1.1,1.0,0.9,0.8,0.9,1.1,0.9
解
根据题意可知,0.9出现的次数最多,因此,0.9是这组数据的众数.
2. 某班30人所穿运动服尺码的情况为:穿75号码的有5人,穿80号码的有6人,穿85号码的有15人,穿90号码的有3人,穿95号码的有1人. 穿哪一种尺码衣服的人最多?这个数据称为什么数?
解
根据题意可知,穿85号衣服的人最多.
因此85号是这组衣服尺码数据的众数.
1.某部队一位新兵连续射靶5次,命中环数如下:
0,2,5,2,7,这组数的中位数是( ).
A.0 B.2 C.5 D.7
2.某篮球队12名队员年龄如下:则这12名队员的中位数是( ).
A.19 B.20 C.21 D.22
年龄(岁) 18 19 20 21 22
人数 1 4 3 2 2
练习题二.
B
B
4.已知数据1、2、x、5的平均数为2.5,则这组数据的中位数与众数分别是____、 ____。
2
2
3.一组数据从小到大排列为-10,-3,0,8,10,15。如果通过增大数据-10来改变该数据的中位数,那么至少使其大于( ).
A.O B.3 C.8 D.10
D
5.某公司有15名员工,他们所在的部门及相应每人所创的年利润如下表所示:
部门 A B C D E F G
人数(个) 1 1 2 4 2 2 3
利润(万元) 20 5 2.5 2.1 1.5 1.5 1.2
⑴.求该公司每人所创年利润的平均数( )万元和中位数( )万元;
⑵.你认为使用平均数和中位数中哪一个来描述
该公司每人所创年利润的一般水平比较合理 ( )
中位数
3.2
2.1
为了反映一组数据的离散程度,可以采用很多方法,统计中常采用以下做法:
方差的定义:设一组数据为x1,x2,…,xn,各数据与 平均数 之差的平方的平均值,叫做这组数据的方差,记做 s2.
即
计算方差的步骤可概括为:
“先平均,后求差,平方后,再平均”.
刘亮和李飞参加射击训练的成绩(单位:环)如下:
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
(1) 两人的平均成绩分别是多少?
(2) 计算这两组数据的方差?
(3) 谁的成绩比较稳定?
刘亮、李飞的射击成绩的方差分别是
计算结果表明: s2李飞> s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
1、已知一组数据为2、0、-1、3、-4,则这组数据的方差为 .
2、甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:甲:7、8、6、8、6、5、9、10、7、4
乙:9、5、7、8、7、6、8、6、7、7
经过计算,两人射击环数的平均数相同,但 S S ,所以确定__去参加比赛。
练习题三.
S2=6
>
乙
3.甲、乙两台机床生产同种零件,10天出的次品分别是
甲:0、1、0、2、2、0、3、1、2、4
乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,
根据你的计算判断哪台机床的性能较好?
4.从甲、乙两种农作物中各抽取10株苗,分别测得它的苗高如下:(单位:cm)
甲:9、10、11、12、7、13、10、8、12、8;
乙:8、13、12、11、10、12、7、7、9、11;
问:(1)哪种农作物的苗长的比较高?
(2)哪种农作物的苗长得比较整齐?
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
