浙教版八年级数学下《第4章平行四边形》章末复习课试卷含答案
文档属性
| 名称 | 浙教版八年级数学下《第4章平行四边形》章末复习课试卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-28 00:00:00 | ||
图片预览


文档简介
章末复习课
考点 1 多边形的内角和与外角和
1.若一个多边形的内角和为1440°,则这个多边形的边数是( )
A.8 B.10 C.12 D.14
2.若多边形的每一个外角的度数都为72°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
3.已知一个多边形的内角和与外角和之比为11∶2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
考点 2 平行四边形的性质及其判定
4.2018·台州如图,在ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A. B.1 C. D.
第4题图
第5题图
5.如图所示,ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )
A.2 B.3 C.4 D.6
6.如图所示,ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( )
A.3 cm B.4 cm
C.5 cm D.8 cm
第6题图
第7题图
7.2018·临沂如图,在ABCD中,AB=10,AD=6,AC⊥BC.则BD=____.
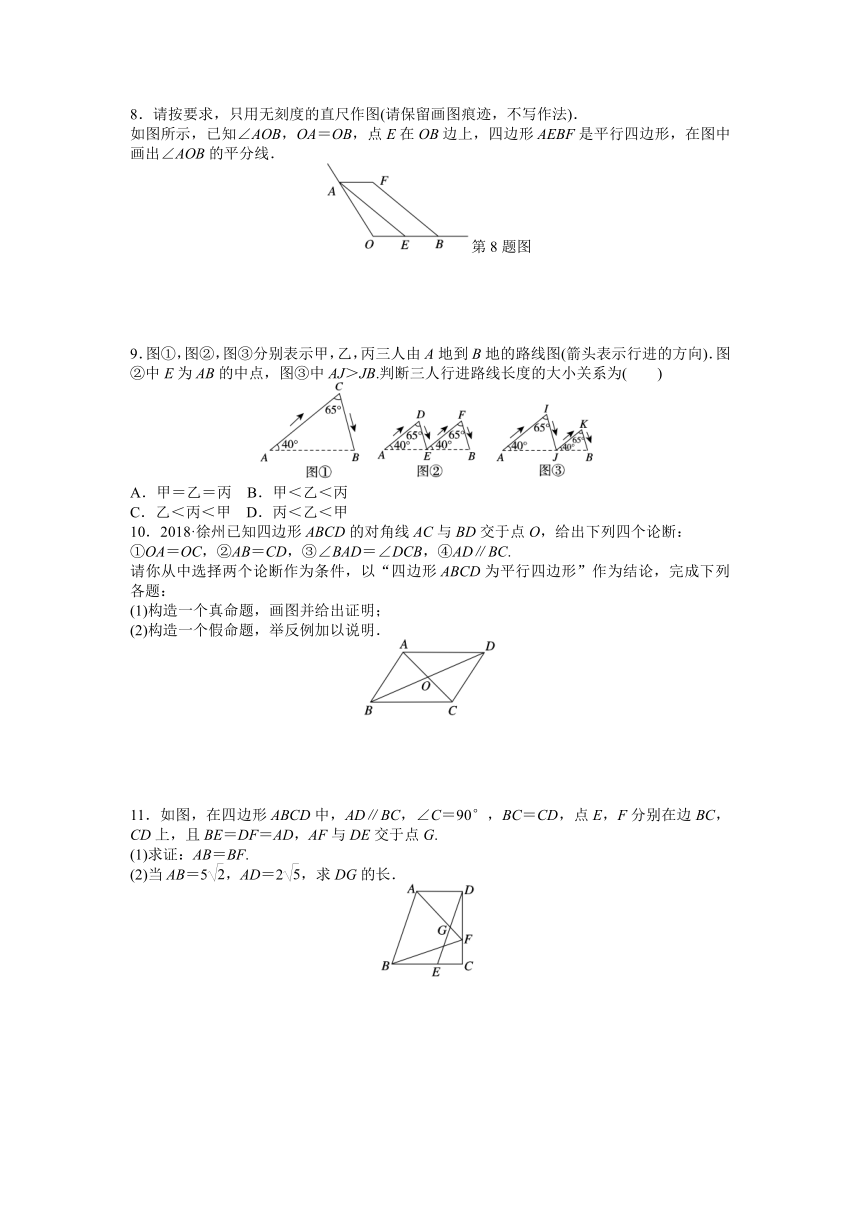
8.请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法).
如图所示,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.
第8题图
9.图①,图②,图③分别表示甲,乙,丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( )
A.甲=乙=丙 B.甲<乙<丙
C.乙<丙<甲 D.丙<乙<甲
10.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
11.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,且BE=DF=AD,AF与DE交于点G.
(1)求证:AB=BF.
(2)当AB=5,AD=2,求DG的长.
考点3 中心对称与中心对称图形
12.如图所示是4×4正方形网格,请在其中选取一个白色的单位正方形并涂阴影,使图中阴影部分成中心对称图形.
13.在平面直角坐标系中,以O,A,B,C为顶点的平行四边形的顶点为O(0,0),A(6,0),B(2,2),C(-4,2),直线y=kx+2平分平行四边形的周长,则k的值为____.
考点4 三角形的中位线
14.如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连结四边形ABCD各边的中点,得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…;如此进行下去,得到四边形A7B7C7D7,那么四边形A7B7C7D7的周长为____.
15.△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点,
求证:EF∥DG,且EF=DG.
第15题图
考点5 反证法
16.用反证法证明:一个三角形中不能有两个直角.
参考答案
章末复习课
考点 1 多边形的内角和与外角和
1.若一个多边形的内角和为1440°,则这个多边形的边数是( B )
A.8 B.10 C.12 D.14
2.若多边形的每一个外角的度数都为72°,则这个多边形的边数为( B )
A.4 B.5 C.6 D.7
3.已知一个多边形的内角和与外角和之比为11∶2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
【答案】 (1)这个多边形的内角和为1980°.
(2)这个多边形的边数为13.
考点 2 平行四边形的性质及其判定
4.2018·台州如图,在ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( B )
A. B.1 C. D.
第4题图
第5题图
5.如图所示,ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( A )
A.2 B.3 C.4 D.6
6.如图所示,ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( B )
A.3 cm B.4 cm
C.5 cm D.8 cm
第6题图
第7题图
7.2018·临沂如图,在ABCD中,AB=10,AD=6,AC⊥BC.则BD=__4__.
8.请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法).
如图所示,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.
第8题图
第8题答图
解:如图所示,
连结AB,EF交于点D,作射线OD,
则射线OD为∠AOB的平分线.
9.图①,图②,图③分别表示甲,乙,丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( A )
A.甲=乙=丙 B.甲<乙<丙
C.乙<丙<甲 D.丙<乙<甲
【解析】 图①中,甲走的路线长是AC+BC;
图②中,延长AD和BF交于点C.
∵∠DAE=∠FEB=40°,
∴AD∥EF,则DC∥EF.
同理DE∥CF,
∴四边形CDEF是平行四边形,∴EF=CD,DE=CF.
即乙走的路线长是AD+DE+EF+FB=AD+CF+CD+FB=AC+BC;
图③中,延长AI和BK交于点C.
与以上证明过程类似IC=JK,CK=IJ,
即丙走的路线长是AI+IJ+JK+KB=AI+CK+IC+BK=AC+BC;
即甲=乙=丙,故选:A.
10.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
解:(1)选择①④为条件时:
∵AD∥BC,
∴∠DAC=∠BCA,∠ADB=∠DBC.
又∵OA=OC,
∴△AOD≌△COB.
∴AD=BC.
∴四边形ABCD为平行四边形.
(2)选择②④为条件时,此时一组对边平行,另一组对边相等,可以构成等腰梯形.
11.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,且BE=DF=AD,AF与DE交于点G.
(1)求证:AB=BF.
(2)当AB=5,AD=2,求DG的长.
解:(1)证明:∵BC=CD,BE=DF,
∴CF=CE.
在△BCF与△DCE中,
∵
∴△BCF≌△DCE,∴BF=DE.
∵AD∥BC,BE=AD,
∴四边形ABED是平行四边形.
∴AB=DE,∴AB=BF.
(2)由(1)可得AB=DE=5,设EC=FC=x,
在Rt△DEC中,由勾股定理可得x2+(x+2)2=(5)2,
解,得x=,
延长AF交BC延长线于点H,
∵AD∥BC,∴∠1=∠H.
∵AD=DF,∴∠1=∠2.
∵∠2=∠3,∴∠3=∠H,∴FC=CH.
∴EH=2x=2,∴AD=EH.
连结AE,DH.
∵AD∥BC,∴四边形AEHD是平行四边形,∴DG=EG.
∴DG=DE=.
考点3 中心对称与中心对称图形
12.如图所示是4×4正方形网格,请在其中选取一个白色的单位正方形并涂阴影,使图中阴影部分成中心对称图形.
【答案】 略
13.在平面直角坐标系中,以O,A,B,C为顶点的平行四边形的顶点为O(0,0),A(6,0),B(2,2),C(-4,2),直线y=kx+2平分平行四边形的周长,则k的值为__-1__.
考点4 三角形的中位线
14.如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连结四边形ABCD各边的中点,得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…;如此进行下去,得到四边形A7B7C7D7,那么四边形A7B7C7D7的周长为____.
解:根据中位线的性质易知,A7B7=A5B5;A5B5=A3B3;A3B3=A1B1;A1B1=AC;
故可得A7B7=×××AC=;
同理,可得B7C7=;
故四边形A7B7C7D7的周长是2×=.
15.△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点,
求证:EF∥DG,且EF=DG.
第15题图 第15题答图
证明:连结DE,FG,
∵BD,CE是△ABC的中位线,
∴D,E分别是AC,AB的中点,
∴DE∥BC,DE=BC.
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
考点5 反证法
16.用反证法证明:一个三角形中不能有两个直角.
证明:假设三角形的三个内角A,B,C中有两个直角,不妨设∠A=∠B=90°,
则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,
∴∠A=∠B=90°不成立;
所以一个三角形中不能有两个直角.
考点 1 多边形的内角和与外角和
1.若一个多边形的内角和为1440°,则这个多边形的边数是( )
A.8 B.10 C.12 D.14
2.若多边形的每一个外角的度数都为72°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
3.已知一个多边形的内角和与外角和之比为11∶2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
考点 2 平行四边形的性质及其判定
4.2018·台州如图,在ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A. B.1 C. D.
第4题图
第5题图
5.如图所示,ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )
A.2 B.3 C.4 D.6
6.如图所示,ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( )
A.3 cm B.4 cm
C.5 cm D.8 cm
第6题图
第7题图
7.2018·临沂如图,在ABCD中,AB=10,AD=6,AC⊥BC.则BD=____.
8.请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法).
如图所示,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.
第8题图
9.图①,图②,图③分别表示甲,乙,丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( )
A.甲=乙=丙 B.甲<乙<丙
C.乙<丙<甲 D.丙<乙<甲
10.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
11.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,且BE=DF=AD,AF与DE交于点G.
(1)求证:AB=BF.
(2)当AB=5,AD=2,求DG的长.
考点3 中心对称与中心对称图形
12.如图所示是4×4正方形网格,请在其中选取一个白色的单位正方形并涂阴影,使图中阴影部分成中心对称图形.
13.在平面直角坐标系中,以O,A,B,C为顶点的平行四边形的顶点为O(0,0),A(6,0),B(2,2),C(-4,2),直线y=kx+2平分平行四边形的周长,则k的值为____.
考点4 三角形的中位线
14.如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连结四边形ABCD各边的中点,得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…;如此进行下去,得到四边形A7B7C7D7,那么四边形A7B7C7D7的周长为____.
15.△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点,
求证:EF∥DG,且EF=DG.
第15题图
考点5 反证法
16.用反证法证明:一个三角形中不能有两个直角.
参考答案
章末复习课
考点 1 多边形的内角和与外角和
1.若一个多边形的内角和为1440°,则这个多边形的边数是( B )
A.8 B.10 C.12 D.14
2.若多边形的每一个外角的度数都为72°,则这个多边形的边数为( B )
A.4 B.5 C.6 D.7
3.已知一个多边形的内角和与外角和之比为11∶2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
【答案】 (1)这个多边形的内角和为1980°.
(2)这个多边形的边数为13.
考点 2 平行四边形的性质及其判定
4.2018·台州如图,在ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( B )
A. B.1 C. D.
第4题图
第5题图
5.如图所示,ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( A )
A.2 B.3 C.4 D.6
6.如图所示,ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( B )
A.3 cm B.4 cm
C.5 cm D.8 cm
第6题图
第7题图
7.2018·临沂如图,在ABCD中,AB=10,AD=6,AC⊥BC.则BD=__4__.
8.请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法).
如图所示,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.
第8题图
第8题答图
解:如图所示,
连结AB,EF交于点D,作射线OD,
则射线OD为∠AOB的平分线.
9.图①,图②,图③分别表示甲,乙,丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( A )
A.甲=乙=丙 B.甲<乙<丙
C.乙<丙<甲 D.丙<乙<甲
【解析】 图①中,甲走的路线长是AC+BC;
图②中,延长AD和BF交于点C.
∵∠DAE=∠FEB=40°,
∴AD∥EF,则DC∥EF.
同理DE∥CF,
∴四边形CDEF是平行四边形,∴EF=CD,DE=CF.
即乙走的路线长是AD+DE+EF+FB=AD+CF+CD+FB=AC+BC;
图③中,延长AI和BK交于点C.
与以上证明过程类似IC=JK,CK=IJ,
即丙走的路线长是AI+IJ+JK+KB=AI+CK+IC+BK=AC+BC;
即甲=乙=丙,故选:A.
10.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
解:(1)选择①④为条件时:
∵AD∥BC,
∴∠DAC=∠BCA,∠ADB=∠DBC.
又∵OA=OC,
∴△AOD≌△COB.
∴AD=BC.
∴四边形ABCD为平行四边形.
(2)选择②④为条件时,此时一组对边平行,另一组对边相等,可以构成等腰梯形.
11.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,且BE=DF=AD,AF与DE交于点G.
(1)求证:AB=BF.
(2)当AB=5,AD=2,求DG的长.
解:(1)证明:∵BC=CD,BE=DF,
∴CF=CE.
在△BCF与△DCE中,
∵
∴△BCF≌△DCE,∴BF=DE.
∵AD∥BC,BE=AD,
∴四边形ABED是平行四边形.
∴AB=DE,∴AB=BF.
(2)由(1)可得AB=DE=5,设EC=FC=x,
在Rt△DEC中,由勾股定理可得x2+(x+2)2=(5)2,
解,得x=,
延长AF交BC延长线于点H,
∵AD∥BC,∴∠1=∠H.
∵AD=DF,∴∠1=∠2.
∵∠2=∠3,∴∠3=∠H,∴FC=CH.
∴EH=2x=2,∴AD=EH.
连结AE,DH.
∵AD∥BC,∴四边形AEHD是平行四边形,∴DG=EG.
∴DG=DE=.
考点3 中心对称与中心对称图形
12.如图所示是4×4正方形网格,请在其中选取一个白色的单位正方形并涂阴影,使图中阴影部分成中心对称图形.
【答案】 略
13.在平面直角坐标系中,以O,A,B,C为顶点的平行四边形的顶点为O(0,0),A(6,0),B(2,2),C(-4,2),直线y=kx+2平分平行四边形的周长,则k的值为__-1__.
考点4 三角形的中位线
14.如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连结四边形ABCD各边的中点,得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…;如此进行下去,得到四边形A7B7C7D7,那么四边形A7B7C7D7的周长为____.
解:根据中位线的性质易知,A7B7=A5B5;A5B5=A3B3;A3B3=A1B1;A1B1=AC;
故可得A7B7=×××AC=;
同理,可得B7C7=;
故四边形A7B7C7D7的周长是2×=.
15.△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点,
求证:EF∥DG,且EF=DG.
第15题图 第15题答图
证明:连结DE,FG,
∵BD,CE是△ABC的中位线,
∴D,E分别是AC,AB的中点,
∴DE∥BC,DE=BC.
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
考点5 反证法
16.用反证法证明:一个三角形中不能有两个直角.
证明:假设三角形的三个内角A,B,C中有两个直角,不妨设∠A=∠B=90°,
则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,
∴∠A=∠B=90°不成立;
所以一个三角形中不能有两个直角.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
