浙教版数学九年级下册 3.4《简单几何体的表面展开图》教案
文档属性
| 名称 | 浙教版数学九年级下册 3.4《简单几何体的表面展开图》教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 161.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 17:38:54 | ||
图片预览

文档简介
《简单几何体的表面展开图》教案
教学目标
1.知道什么是直棱柱的表面展开图;
2.能画出立方体的各种表面展开图;
3.会利用直棱柱表面展开图进行相关计算.
4.了解圆柱和圆锥的概念和性质,认识圆柱和圆锥.
5.了解圆柱和圆锥的侧面展开图,会根据展开图想象实际物体.
6.会计算圆柱和圆锥的侧面积和全面积.
教学重点
1.立方体的表面展开图
2.圆柱的侧面展开图、明晰展开图与原几何体的关系、以及掌握圆柱的侧面积和全面积的计算。
3.圆锥的侧面、底面、高、母线等概念;圆锥的侧面积、全面积计算公式。
教学难点
1.利用直棱柱的表面展开图进行相关计算.
2.圆柱的侧面积和全面积的计算。
3.圆锥的侧面积计算公式解决实际问题。
教学设计
一、几何体的表面展开图
(一)引入
如图,A处有一只蚂蚁,在B处有一粒蜜糖,蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
(二)动手剪一剪]
请将一个立方体纸盒沿某些棱剪开,你能得到立方体怎样的表面展开图?请大家动手试一试.
领悟:
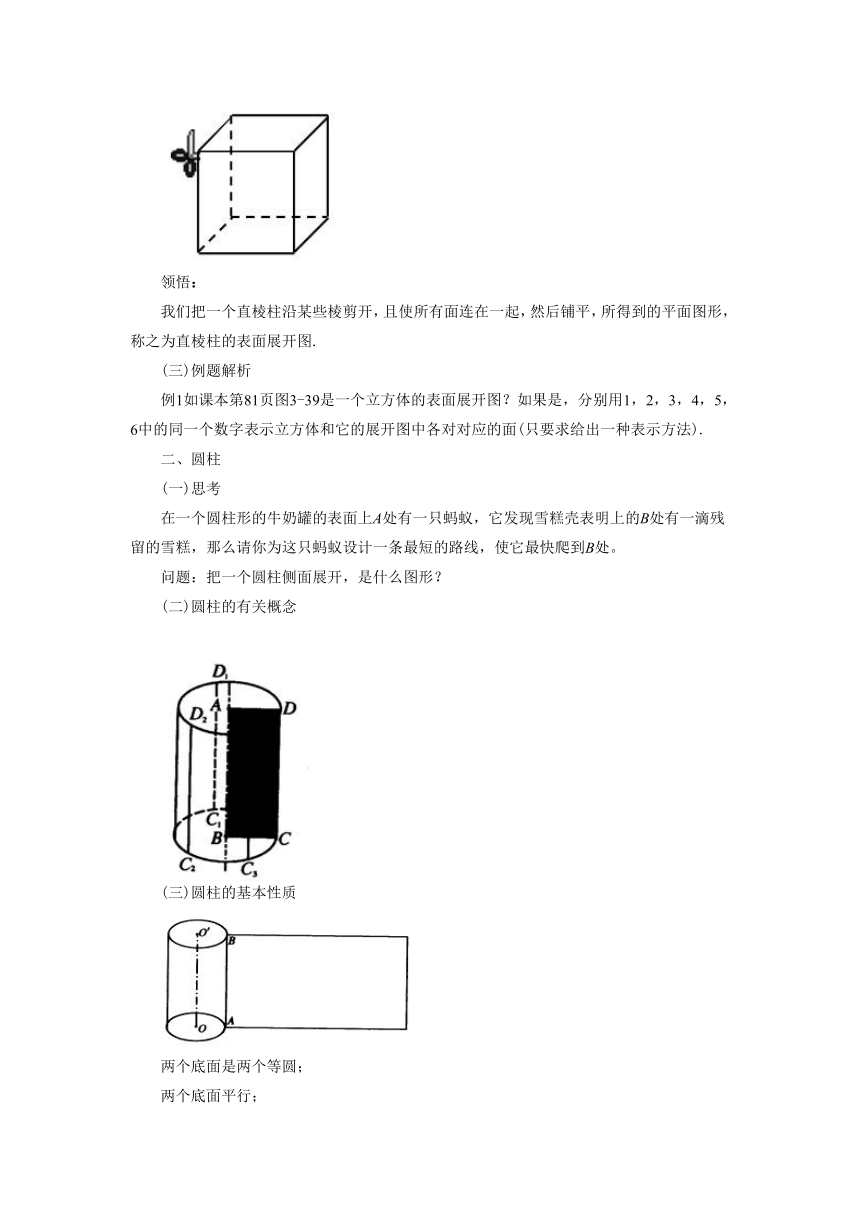
我们把一个直棱柱沿某些棱剪开,且使所有面连在一起,然后铺平,所得到的平面图形,称之为直棱柱的表面展开图.
(三)例题解析
例1如课本第81页图3-39是一个立方体的表面展开图?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示方法).
二、圆柱
(一)思考
在一个圆柱形的牛奶罐的表面上A处有一只蚂蚁,它发现雪糕壳表明上的B处有一滴残留的雪糕,那么请你为这只蚂蚁设计一条最短的路线,使它最快爬到B处。
问题:把一个圆柱侧面展开,是什么图形?
(二)圆柱的有关概念
[
(三)圆柱的基本性质
两个底面是两个等圆;
两个底面平行;
母线平行与轴;
轴通过上、下底面的圆心;
母线长都相等并等于高;
侧面展开图是矩形;
矩形的一边长等于圆柱的高,即母线长;
另一边长是底面圆的周长;
圆柱的侧面积等于底面圆的周长乘以圆柱的高.
(三)例题解析
例3 如课本第85页图3-48为一个圆柱三视图.以相同的比例画出它的表面展开图,并计算它的侧面积和全面积(结果保留π).
三、圆锥
(一)认识圆锥
生活中有许多的形象
(二)生活小问题:
1、做一个铁皮漏斗需要多大一块铁皮?
2、冰淇淋的包装纸面积有多大?
3、杂技团里小丑的帽子需多少布料?
归纳:
实际问题>>面积问题>>图形的形状
(三)圆锥知识知多少
A、圆锥由一个侧面和一个底面构成
B、圆锥的高(h)[
连结圆锥的顶点与底面圆心的线段叫做圆锥的高,如图中的SO。
C、圆锥的母线(a)
圆锥的顶点和底面圆周上任意一点的连线段叫做圆锥的母线,如图中的SA、SB等。
D、圆锥的底面圆的半径(r)]
(4)探究:
如果把一个圆锥的侧面沿它的一条母线剪开, 展开在一个平面上,想一想展开后是什么图形?
根据扇形与圆锥之间的关系填空:
如图,设圆锥的母线长为a,底面半径为r,那么,这个扇形的半径(R)为_________,扇形的弧长为__________,圆锥的侧面积是 弧长为圆锥底面周长的扇形的面积。
扇形的面积公式:
因此圆锥的侧面积(S侧)为:扇形的半径与扇形弧长积的一半。
若圆锥的底面半径为r,母线长为a,则它的侧面积(S侧)为:
圆锥的母线与底面周长积的一半:
(四)例题解析
例4 圆锥形烟囱帽(如课本第88页图3-54)的母线长为80cm,高为38.7cm.
教学目标
1.知道什么是直棱柱的表面展开图;
2.能画出立方体的各种表面展开图;
3.会利用直棱柱表面展开图进行相关计算.
4.了解圆柱和圆锥的概念和性质,认识圆柱和圆锥.
5.了解圆柱和圆锥的侧面展开图,会根据展开图想象实际物体.
6.会计算圆柱和圆锥的侧面积和全面积.
教学重点
1.立方体的表面展开图
2.圆柱的侧面展开图、明晰展开图与原几何体的关系、以及掌握圆柱的侧面积和全面积的计算。
3.圆锥的侧面、底面、高、母线等概念;圆锥的侧面积、全面积计算公式。
教学难点
1.利用直棱柱的表面展开图进行相关计算.
2.圆柱的侧面积和全面积的计算。
3.圆锥的侧面积计算公式解决实际问题。
教学设计
一、几何体的表面展开图
(一)引入
如图,A处有一只蚂蚁,在B处有一粒蜜糖,蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
(二)动手剪一剪]
请将一个立方体纸盒沿某些棱剪开,你能得到立方体怎样的表面展开图?请大家动手试一试.
领悟:
我们把一个直棱柱沿某些棱剪开,且使所有面连在一起,然后铺平,所得到的平面图形,称之为直棱柱的表面展开图.
(三)例题解析
例1如课本第81页图3-39是一个立方体的表面展开图?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示方法).
二、圆柱
(一)思考
在一个圆柱形的牛奶罐的表面上A处有一只蚂蚁,它发现雪糕壳表明上的B处有一滴残留的雪糕,那么请你为这只蚂蚁设计一条最短的路线,使它最快爬到B处。
问题:把一个圆柱侧面展开,是什么图形?
(二)圆柱的有关概念
[
(三)圆柱的基本性质
两个底面是两个等圆;
两个底面平行;
母线平行与轴;
轴通过上、下底面的圆心;
母线长都相等并等于高;
侧面展开图是矩形;
矩形的一边长等于圆柱的高,即母线长;
另一边长是底面圆的周长;
圆柱的侧面积等于底面圆的周长乘以圆柱的高.
(三)例题解析
例3 如课本第85页图3-48为一个圆柱三视图.以相同的比例画出它的表面展开图,并计算它的侧面积和全面积(结果保留π).
三、圆锥
(一)认识圆锥
生活中有许多的形象
(二)生活小问题:
1、做一个铁皮漏斗需要多大一块铁皮?
2、冰淇淋的包装纸面积有多大?
3、杂技团里小丑的帽子需多少布料?
归纳:
实际问题>>面积问题>>图形的形状
(三)圆锥知识知多少
A、圆锥由一个侧面和一个底面构成
B、圆锥的高(h)[
连结圆锥的顶点与底面圆心的线段叫做圆锥的高,如图中的SO。
C、圆锥的母线(a)
圆锥的顶点和底面圆周上任意一点的连线段叫做圆锥的母线,如图中的SA、SB等。
D、圆锥的底面圆的半径(r)]
(4)探究:
如果把一个圆锥的侧面沿它的一条母线剪开, 展开在一个平面上,想一想展开后是什么图形?
根据扇形与圆锥之间的关系填空:
如图,设圆锥的母线长为a,底面半径为r,那么,这个扇形的半径(R)为_________,扇形的弧长为__________,圆锥的侧面积是 弧长为圆锥底面周长的扇形的面积。
扇形的面积公式:
因此圆锥的侧面积(S侧)为:扇形的半径与扇形弧长积的一半。
若圆锥的底面半径为r,母线长为a,则它的侧面积(S侧)为:
圆锥的母线与底面周长积的一半:
(四)例题解析
例4 圆锥形烟囱帽(如课本第88页图3-54)的母线长为80cm,高为38.7cm.
