4.1.1 多边形(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 4.1.1 多边形(知识清单+经典例题+夯实基础+提优训练+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 358.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-02 14:24:33 | ||
图片预览


文档简介
浙江版八年级数学下册第4章平行四边形
4.1 多 边 形
第1课时 多 边 形(1)
【知识清单】
一、多边形
在同一平面内,由不在同一条直线上的若干条线段(线段的条数不小于3)首尾顺次相接形成的图形叫做多边形.
二、构成多边形的元素
组成多边形的各条线段叫做多边形的边.边数为n的多边形叫n边形(n为正整数,且n≥3).
多边形相邻两边组成的角叫做多边形的内角,多边形一边的延长线与相邻的另一边所组成的角叫做多边形的外角.多边形每一个内角的顶点叫做多边形的顶点,连结多边形不相邻两个顶点的线段叫做多变形的对角线.
三、四边形的内角和
四边形的内角和等于360°.
【经典例题】
例题1、如图,在四边形ABCD中,∠α= ,∠β== .
【考点】四边形的内角和.
【分析】根据四边形的内角和为360°和邻补角定义求解即可.
【解答】∵在四边形ABCD中,∠A+∠B+∠BCD+∠ADC=360°,
∴∠ADC =360°∠A∠B∠ACD
=360°105°65°76°=114°,
∴∠α=180°∠ADC =66°,
∴∠β=180°∠BCD=104°.
【点评】点评?本题考查了四边形内角和以及邻补角的定义、熟练掌握四边形内角和以及邻补角的定义是解题的关键.
例题2、如图在四边形ABCD中,AB=BC=AC=AD,则∠BDC的度数为( )
A.10° B.20° C.30° D.40°
【考点】等腰三角形的性质;等边三角形的性质;三角形内角和定理和四边形的内角和定理.
【分析】设∠CBD=x,∠BDC=y,根据AB=BC=AC=AD,再由四边形的内角和是360°得60°+60°+2x+60°+2(60°x+y)=360°,解得即可得出答案.
【解答】解;设∠CBD=x,∠BDC=y,
∵AB=BC=AC=AD,
∴∠ABC=∠BAC=∠ACB=60°,
∠ABD=∠ADB=60°x,∠ACD=∠ADC=60°x+y
∴∠BAD=180°2(60°x)=60°+2x.
∵四边形的内角和为360°,
∴60°+60°+2x+60°+2(60°x+y)=360°,
解得y=30°,∴∠BDC=30°.
故选C.
【点评】此题主要考查学生对四边形的内角和定理(四边形的内角和为360°),等腰三角形的
性质和等边三角形性质的理解和掌握,此题的关键是由已知条件得到60°+60°+2x+60°+2(60°x+y)
=360°,进一步求出结果.
【夯实基础】
1、在四边形的四个内角中,钝角个数最多为( )
A.4 B.3 C.2 D.1
2、四边形ABCD中,∠A=95°,∠B=120°,∠C=75°,则∠D=( )
A. 110° B. 90° C. 80° D. 70°
3、四边形ABCD中,∠A与∠C互为补角,∠B∠D=20°,则∠B∶∠D的度数为( )
A. 4∶3 B.5∶4 C. 6∶5 D. 7∶6
4、如图,一块四边形玻璃破了一角,要想知道破掉的∠C的度数,只要测量∠A,∠B,∠D的度数,就能知道∠C的度数了,其根据是(??)
A. 四边形外角和是360° B. 四边形外角和是180°
C. 四边形内角和是360° D. 四边形内角和是180°
5、在四边形ABCD中,∠A=120°,∠B∶∠C∶∠D=3∶4∶5,则∠D= .
6、如图,四边形各内角平分线分别交于点A,B,C,D,则∠ABC+∠ADC= .
7、在四边形ABCD中,∠D=80°,∠B比∠A大40°,∠C是∠A的3倍,求∠A,∠B,∠C的大小.
8、如图,四边形ABCD中,∠B=∠D,AF平分∠BAD,交DC于点F,E是AB上的点,AF∥CE.求证:CE平分∠BCD.
【提优特训】
9、四边形ABCD中,AD∥BC,那么它的四个内角之比∠A∶∠B∶∠C∶∠D可能是( )
A.3∶4∶8∶9 B.8∶3∶4∶9 C.9∶3∶4∶8 D.9∶4∶8∶3
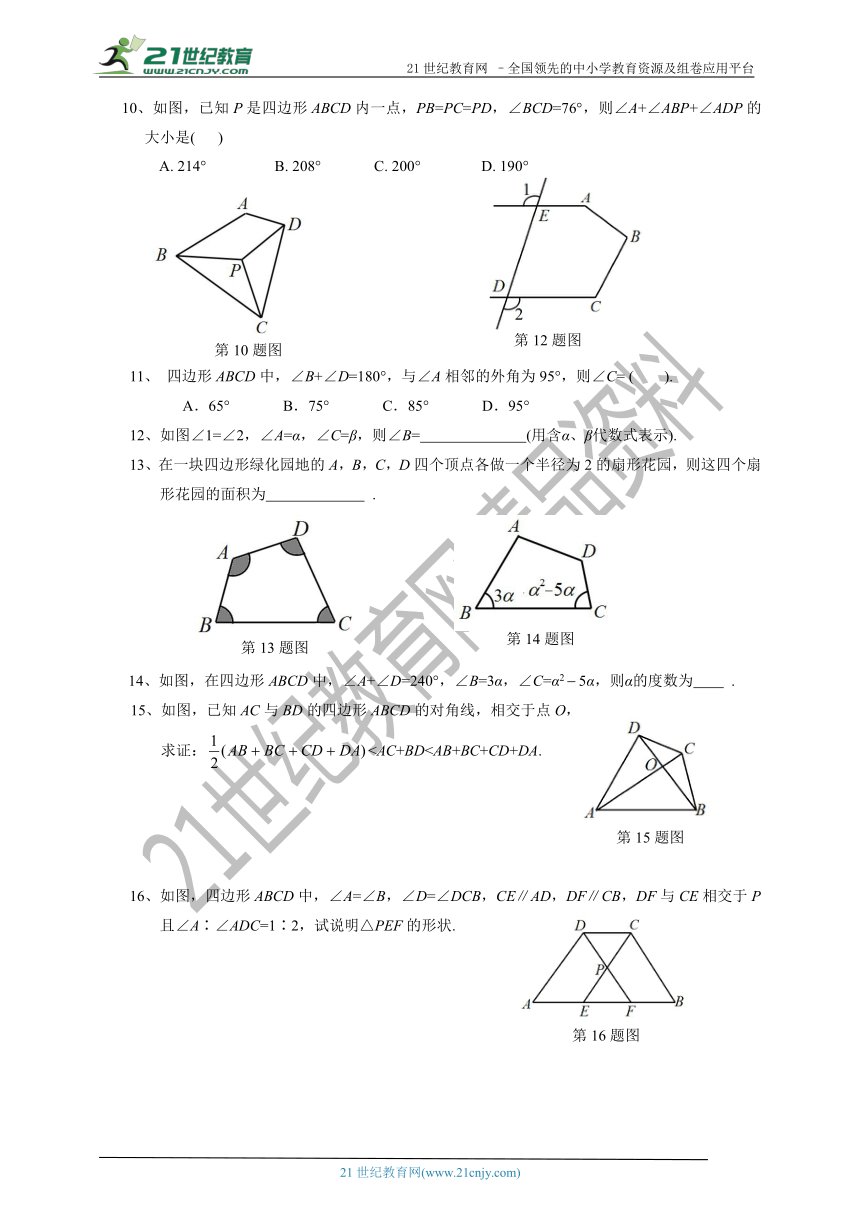
10、如图,已知P是四边形ABCD内一点,PB=PC=PD,∠BCD=76°,则∠A+∠ABP+∠ADP的大小是( )
A. 214° B. 208° C. 200° D. 190°
11、 四边形ABCD中,∠B+∠D=180°,与∠A相邻的外角为95°,则∠C= ( ).
A.65° B.75° C.85° D.95°
12、如图∠1=∠2,∠A=α,∠C=β,则∠B= (用含α、β代数式表示).
13、在一块四边形绿化园地的A,B,C,D四个顶点各做一个半径为2的扇形花园,则这四个扇形花园的面积为 .
14、如图,在四边形ABCD中,∠A+∠D=240°,∠B=3α,∠C=α25α,则α的度数为 .
15、如图,已知AC与BD的四边形ABCD的对角线,相交于点O,
求证:16、如图,四边形ABCD中,∠A=∠B,∠D=∠DCB,CE∥AD,DF∥CB,DF与CE相交于P
且∠A∶∠ADC=1∶2,试说明△PEF的形状.
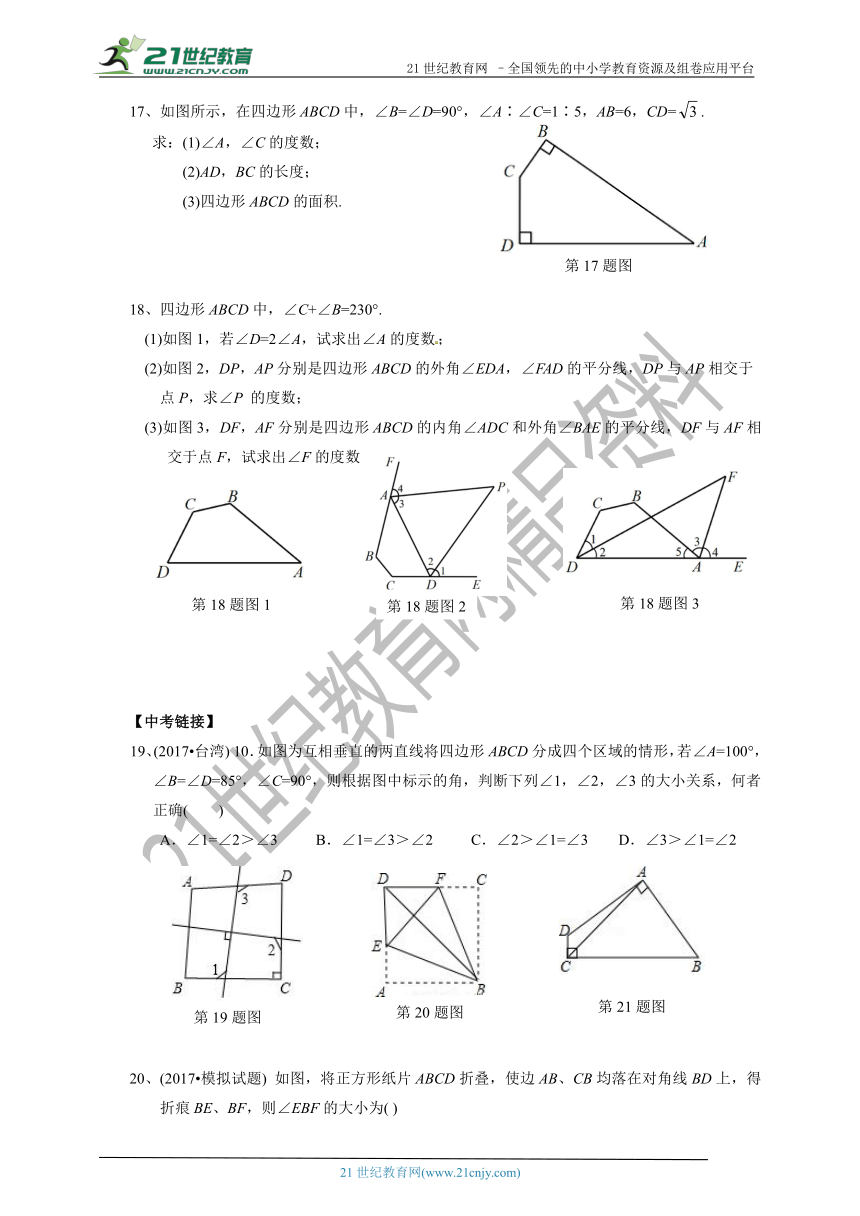
17、如图所示,在四边形ABCD中,∠B=∠D=90°,∠A∶∠C=1∶5,AB=6,CD=.
求:(1)∠A,∠C的度数;
(2)AD,BC的长度;
(3)四边形ABCD的面积.
18、四边形ABCD中,∠C+∠B=230°.
(1)如图1,若∠D=2∠A,试求出∠A的度数;
(2)如图2,DP,AP分别是四边形ABCD的外角∠EDA,∠FAD的平分线,DP与AP相交于
点P,求∠P 的度数;
(3)如图3,DF,AF分别是四边形ABCD的内角∠ADC和外角∠BAE的平分线,DF与AF相交于点F,试求出∠F的度数.
【中考链接】
19、(2017?台湾) 10.如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
A.∠1=∠2>∠3 B.∠1=∠3>∠2 C.∠2>∠1=∠3 D.∠3>∠1=∠2
20、(2017?模拟试题) 如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为( )
A.15° B.30° C.45° D.60°
21、(2018?龙东地区) 7.18.(3.00分)如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
A.15 B.12.5 C.14.5 D.17
22、(2018?模拟试题) 如图,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交而形成的锐角.
①如图1,若α+β>180°,求∠P的度数.(用α、β的代数式表示)
②如图2,若α+β<180°,请在图③中画出∠P,并求证: ∠P=90°.(用α、β的代数式表示)
参考答案
1、B 2、D 3、B 4、C 5、100° 6、180° 9、C 10、B 11、D
12、360°(α+β) 13、 14、12° 19、D 20、C 21、B
7、在四边形ABCD中,∠D=80°,∠B比∠A大40°,∠C是∠A的3倍,求∠A,∠B,∠C的大小.
解:∵四边形ABCD的内角和为360°,∠D=80°,
∴,
解得∠A=48°,∠B=88°,∠C=144°.
∴∠A,∠B,∠C的大小分别为48°,88°,144°.
8、如图,四边形ABCD中,∠B=∠D,AF平分∠BAD,交DC于点F,E是AB上的点,AF∥CE.求证:CE平分∠BCD.
证明:∵四边形ABCD的内角和为360°,∠B=∠D,
∴∠BAD+∠BCD=360°∠B∠D
=360°2∠B,
∵AF平分∠BAD,
∴∠1=∠2.
∵AF∥CE,
∴∠2+∠CEA=180°,
∵∠CEA=∠B+∠4,
∴∠2+∠B+∠4=180°.
∵∠3+∠AFC=180°,
∴∠AFC=∠1+∠D,
∴∠3+∠1+∠D=180°,
∴∠2+∠B+∠4=∠3+∠1+∠D.
∴∠3=∠4.
∴CE平分∠BCD.
15、如图,已知AC与BD的四边形ABCD的对角线,相交于点O,
求证:证明:在△AOB中,OA+OB>AB,
同理OB+OC>BC,OC+OD>CD,OD+OA>DA,
∴ 2(OA+OB+OC+OD)>AB+BC+CD+DA,
∴2(AC+BD) >AB+BC+CD+DA,
∴ 在△ABC中,AC同理AC∴2(AC+BD)<2(AB+BC+CD+DA)
∴AC+BD∴16、如图,四边形ABCD中,∠A=∠B,∠D=∠DCB,CE∥AD,DF∥CB,DF与CE相交于P
且∠A∶∠ADC=1∶2,试说明△PEF的形状.
解:△PEF是等边三角形,理由如下:
∵四边形ABCD的内角和为360°,∠A=∠B,∠ADC=∠DCB,
∴∠A+∠B+∠ADC+∠DCB=360°,
即2(∠A+∠ADC) =360°,
∴∠A+∠ADC=180°.
∵∠A∶∠ADC=1∶2
∴∠A=∠B=60°,
∵CE∥AD,
∴∠CEB=∠A=60°.
同理∠AFD=∠B=60°.
∴△PEF是等边三角形.
17、如图所示,在四边形ABCD中,∠B=∠D=90°,∠A∶∠C=1∶5,AB=6,CD=.
求:(1)∠A,∠C的度数;
(2)AD,BC的长度;
(3)四边形ABCD的面积.
解:延长BC与AD相交于点E.
(1)∵四边形ABCD的内角和为360°,
∠B=∠D=90°,
∴∠A+∠C=180°
∵∠A∶∠C=1∶5,
∴∠A=30°,∠C=150°.
(2)在Rt△ABE中,∠A=30°,
∴∠E=60°,
∴AE=2BE,
∴AE2BE2=AB2
∴3BE2=62
∵BE >0,∴BE=,
∴AE=.
在Rt△CDE中,∠E=60°,
∴∠ECD=30°,
∴CE=2DE,
∴CE2DE2=CD2
∴3DE2=
∵DE>0,∴DE=1,∴EC=2.
∴AD=AEED=1,
∴BC=BECE=2.
(3)S△ABE,
S△CDE,
四边形ABCD的面积= S△ABES△CDE=.
18、四边形ABCD中,∠C+∠B=230°.
(1)如图1,若∠D=2∠A,试求出∠A的度数;
(2)如图2,DP,AP分别是四边形ABCD的外角∠EDA,∠FAD的平分线,DP与AP相交于点P,
求∠P 的度数;
(3)如图3,DF,AF分别是四边形ABCD的内角∠ADC和外角∠BAE的平分线,DF与AF相交于点F,试求出∠F的度数.
解:(1)∵四边形ABCD的内角和为360°,∠C+∠B=230°,
∴∠A+∠D=360°(∠C+∠B)=130°,
∵∠D=2∠A
∴∠A=.
(2)由(1) ∠BAD+∠CDA=130°,
∴∠EDA+∠FAD=230°
∵DP,AP分别是四边形ABCD的外角∠EDA,∠FAD的平分线,
∴∠1=∠2=,∠3=∠4=.
∴∠2+∠3=+=115°
∴∠P=180°(∠2+∠3)=65°.
(3) 由(1) ∠BAD+∠CDA=130°,
即∠1+∠2+∠5=130°.
∵DF,AF分别是四边形ABCD的内角∠ADC和外角∠BAE的平分线,
∴∠1=∠2=,∠3=∠4=.
∴∠F=180°(∠2+∠3+∠5)
=180°(++∠5)
=180°()
=180°90°65°=25°.
22、(2018?模拟试题) 如图,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交而形成的锐角.
①如图1,若α+β>180°,求∠P的度数.(用α、β的代数式表示)
②如图2,若α+β<180°,请在图③中画出∠P,并求证: ∠P=90°.(用α、β的代数式表示)
?解:(1)∵∠ABC+∠DCB=360°(α+β),
∴∠ABC+(180°∠DCE)=360°(α+β)
=2∠FBC+(180°2∠DCP)
=180°2(∠DCP∠FBC)
=180°2∠P,
∴360°(α+β)=180°2∠P,
2∠P=α+β180°,
∴∠P=90°;
(2)∵∠ABC+∠DCB=360°(α+β),
∴∠ABC+(180°∠DCE)=360°(α+β)
=2∠GBC+(180°2∠HCE)
=180°+2(∠GBC∠HCE)
=180°+2∠P,
∴360°(α+β)=180°+2∠P,
∴∠P=90°;故答案为:90°.
4.1 多 边 形
第1课时 多 边 形(1)
【知识清单】
一、多边形
在同一平面内,由不在同一条直线上的若干条线段(线段的条数不小于3)首尾顺次相接形成的图形叫做多边形.
二、构成多边形的元素
组成多边形的各条线段叫做多边形的边.边数为n的多边形叫n边形(n为正整数,且n≥3).
多边形相邻两边组成的角叫做多边形的内角,多边形一边的延长线与相邻的另一边所组成的角叫做多边形的外角.多边形每一个内角的顶点叫做多边形的顶点,连结多边形不相邻两个顶点的线段叫做多变形的对角线.
三、四边形的内角和
四边形的内角和等于360°.
【经典例题】
例题1、如图,在四边形ABCD中,∠α= ,∠β== .
【考点】四边形的内角和.
【分析】根据四边形的内角和为360°和邻补角定义求解即可.
【解答】∵在四边形ABCD中,∠A+∠B+∠BCD+∠ADC=360°,
∴∠ADC =360°∠A∠B∠ACD
=360°105°65°76°=114°,
∴∠α=180°∠ADC =66°,
∴∠β=180°∠BCD=104°.
【点评】点评?本题考查了四边形内角和以及邻补角的定义、熟练掌握四边形内角和以及邻补角的定义是解题的关键.
例题2、如图在四边形ABCD中,AB=BC=AC=AD,则∠BDC的度数为( )
A.10° B.20° C.30° D.40°
【考点】等腰三角形的性质;等边三角形的性质;三角形内角和定理和四边形的内角和定理.
【分析】设∠CBD=x,∠BDC=y,根据AB=BC=AC=AD,再由四边形的内角和是360°得60°+60°+2x+60°+2(60°x+y)=360°,解得即可得出答案.
【解答】解;设∠CBD=x,∠BDC=y,
∵AB=BC=AC=AD,
∴∠ABC=∠BAC=∠ACB=60°,
∠ABD=∠ADB=60°x,∠ACD=∠ADC=60°x+y
∴∠BAD=180°2(60°x)=60°+2x.
∵四边形的内角和为360°,
∴60°+60°+2x+60°+2(60°x+y)=360°,
解得y=30°,∴∠BDC=30°.
故选C.
【点评】此题主要考查学生对四边形的内角和定理(四边形的内角和为360°),等腰三角形的
性质和等边三角形性质的理解和掌握,此题的关键是由已知条件得到60°+60°+2x+60°+2(60°x+y)
=360°,进一步求出结果.
【夯实基础】
1、在四边形的四个内角中,钝角个数最多为( )
A.4 B.3 C.2 D.1
2、四边形ABCD中,∠A=95°,∠B=120°,∠C=75°,则∠D=( )
A. 110° B. 90° C. 80° D. 70°
3、四边形ABCD中,∠A与∠C互为补角,∠B∠D=20°,则∠B∶∠D的度数为( )
A. 4∶3 B.5∶4 C. 6∶5 D. 7∶6
4、如图,一块四边形玻璃破了一角,要想知道破掉的∠C的度数,只要测量∠A,∠B,∠D的度数,就能知道∠C的度数了,其根据是(??)
A. 四边形外角和是360° B. 四边形外角和是180°
C. 四边形内角和是360° D. 四边形内角和是180°
5、在四边形ABCD中,∠A=120°,∠B∶∠C∶∠D=3∶4∶5,则∠D= .
6、如图,四边形各内角平分线分别交于点A,B,C,D,则∠ABC+∠ADC= .
7、在四边形ABCD中,∠D=80°,∠B比∠A大40°,∠C是∠A的3倍,求∠A,∠B,∠C的大小.
8、如图,四边形ABCD中,∠B=∠D,AF平分∠BAD,交DC于点F,E是AB上的点,AF∥CE.求证:CE平分∠BCD.
【提优特训】
9、四边形ABCD中,AD∥BC,那么它的四个内角之比∠A∶∠B∶∠C∶∠D可能是( )
A.3∶4∶8∶9 B.8∶3∶4∶9 C.9∶3∶4∶8 D.9∶4∶8∶3
10、如图,已知P是四边形ABCD内一点,PB=PC=PD,∠BCD=76°,则∠A+∠ABP+∠ADP的大小是( )
A. 214° B. 208° C. 200° D. 190°
11、 四边形ABCD中,∠B+∠D=180°,与∠A相邻的外角为95°,则∠C= ( ).
A.65° B.75° C.85° D.95°
12、如图∠1=∠2,∠A=α,∠C=β,则∠B= (用含α、β代数式表示).
13、在一块四边形绿化园地的A,B,C,D四个顶点各做一个半径为2的扇形花园,则这四个扇形花园的面积为 .
14、如图,在四边形ABCD中,∠A+∠D=240°,∠B=3α,∠C=α25α,则α的度数为 .
15、如图,已知AC与BD的四边形ABCD的对角线,相交于点O,
求证:
且∠A∶∠ADC=1∶2,试说明△PEF的形状.
17、如图所示,在四边形ABCD中,∠B=∠D=90°,∠A∶∠C=1∶5,AB=6,CD=.
求:(1)∠A,∠C的度数;
(2)AD,BC的长度;
(3)四边形ABCD的面积.
18、四边形ABCD中,∠C+∠B=230°.
(1)如图1,若∠D=2∠A,试求出∠A的度数;
(2)如图2,DP,AP分别是四边形ABCD的外角∠EDA,∠FAD的平分线,DP与AP相交于
点P,求∠P 的度数;
(3)如图3,DF,AF分别是四边形ABCD的内角∠ADC和外角∠BAE的平分线,DF与AF相交于点F,试求出∠F的度数.
【中考链接】
19、(2017?台湾) 10.如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
A.∠1=∠2>∠3 B.∠1=∠3>∠2 C.∠2>∠1=∠3 D.∠3>∠1=∠2
20、(2017?模拟试题) 如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为( )
A.15° B.30° C.45° D.60°
21、(2018?龙东地区) 7.18.(3.00分)如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
A.15 B.12.5 C.14.5 D.17
22、(2018?模拟试题) 如图,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交而形成的锐角.
①如图1,若α+β>180°,求∠P的度数.(用α、β的代数式表示)
②如图2,若α+β<180°,请在图③中画出∠P,并求证: ∠P=90°.(用α、β的代数式表示)
参考答案
1、B 2、D 3、B 4、C 5、100° 6、180° 9、C 10、B 11、D
12、360°(α+β) 13、 14、12° 19、D 20、C 21、B
7、在四边形ABCD中,∠D=80°,∠B比∠A大40°,∠C是∠A的3倍,求∠A,∠B,∠C的大小.
解:∵四边形ABCD的内角和为360°,∠D=80°,
∴,
解得∠A=48°,∠B=88°,∠C=144°.
∴∠A,∠B,∠C的大小分别为48°,88°,144°.
8、如图,四边形ABCD中,∠B=∠D,AF平分∠BAD,交DC于点F,E是AB上的点,AF∥CE.求证:CE平分∠BCD.
证明:∵四边形ABCD的内角和为360°,∠B=∠D,
∴∠BAD+∠BCD=360°∠B∠D
=360°2∠B,
∵AF平分∠BAD,
∴∠1=∠2.
∵AF∥CE,
∴∠2+∠CEA=180°,
∵∠CEA=∠B+∠4,
∴∠2+∠B+∠4=180°.
∵∠3+∠AFC=180°,
∴∠AFC=∠1+∠D,
∴∠3+∠1+∠D=180°,
∴∠2+∠B+∠4=∠3+∠1+∠D.
∴∠3=∠4.
∴CE平分∠BCD.
15、如图,已知AC与BD的四边形ABCD的对角线,相交于点O,
求证:
同理OB+OC>BC,OC+OD>CD,OD+OA>DA,
∴ 2(OA+OB+OC+OD)>AB+BC+CD+DA,
∴2(AC+BD) >AB+BC+CD+DA,
∴
∴AC+BD
且∠A∶∠ADC=1∶2,试说明△PEF的形状.
解:△PEF是等边三角形,理由如下:
∵四边形ABCD的内角和为360°,∠A=∠B,∠ADC=∠DCB,
∴∠A+∠B+∠ADC+∠DCB=360°,
即2(∠A+∠ADC) =360°,
∴∠A+∠ADC=180°.
∵∠A∶∠ADC=1∶2
∴∠A=∠B=60°,
∵CE∥AD,
∴∠CEB=∠A=60°.
同理∠AFD=∠B=60°.
∴△PEF是等边三角形.
17、如图所示,在四边形ABCD中,∠B=∠D=90°,∠A∶∠C=1∶5,AB=6,CD=.
求:(1)∠A,∠C的度数;
(2)AD,BC的长度;
(3)四边形ABCD的面积.
解:延长BC与AD相交于点E.
(1)∵四边形ABCD的内角和为360°,
∠B=∠D=90°,
∴∠A+∠C=180°
∵∠A∶∠C=1∶5,
∴∠A=30°,∠C=150°.
(2)在Rt△ABE中,∠A=30°,
∴∠E=60°,
∴AE=2BE,
∴AE2BE2=AB2
∴3BE2=62
∵BE >0,∴BE=,
∴AE=.
在Rt△CDE中,∠E=60°,
∴∠ECD=30°,
∴CE=2DE,
∴CE2DE2=CD2
∴3DE2=
∵DE>0,∴DE=1,∴EC=2.
∴AD=AEED=1,
∴BC=BECE=2.
(3)S△ABE,
S△CDE,
四边形ABCD的面积= S△ABES△CDE=.
18、四边形ABCD中,∠C+∠B=230°.
(1)如图1,若∠D=2∠A,试求出∠A的度数;
(2)如图2,DP,AP分别是四边形ABCD的外角∠EDA,∠FAD的平分线,DP与AP相交于点P,
求∠P 的度数;
(3)如图3,DF,AF分别是四边形ABCD的内角∠ADC和外角∠BAE的平分线,DF与AF相交于点F,试求出∠F的度数.
解:(1)∵四边形ABCD的内角和为360°,∠C+∠B=230°,
∴∠A+∠D=360°(∠C+∠B)=130°,
∵∠D=2∠A
∴∠A=.
(2)由(1) ∠BAD+∠CDA=130°,
∴∠EDA+∠FAD=230°
∵DP,AP分别是四边形ABCD的外角∠EDA,∠FAD的平分线,
∴∠1=∠2=,∠3=∠4=.
∴∠2+∠3=+=115°
∴∠P=180°(∠2+∠3)=65°.
(3) 由(1) ∠BAD+∠CDA=130°,
即∠1+∠2+∠5=130°.
∵DF,AF分别是四边形ABCD的内角∠ADC和外角∠BAE的平分线,
∴∠1=∠2=,∠3=∠4=.
∴∠F=180°(∠2+∠3+∠5)
=180°(++∠5)
=180°()
=180°90°65°=25°.
22、(2018?模拟试题) 如图,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交而形成的锐角.
①如图1,若α+β>180°,求∠P的度数.(用α、β的代数式表示)
②如图2,若α+β<180°,请在图③中画出∠P,并求证: ∠P=90°.(用α、β的代数式表示)
?解:(1)∵∠ABC+∠DCB=360°(α+β),
∴∠ABC+(180°∠DCE)=360°(α+β)
=2∠FBC+(180°2∠DCP)
=180°2(∠DCP∠FBC)
=180°2∠P,
∴360°(α+β)=180°2∠P,
2∠P=α+β180°,
∴∠P=90°;
(2)∵∠ABC+∠DCB=360°(α+β),
∴∠ABC+(180°∠DCE)=360°(α+β)
=2∠GBC+(180°2∠HCE)
=180°+2(∠GBC∠HCE)
=180°+2∠P,
∴360°(α+β)=180°+2∠P,
∴∠P=90°;故答案为:90°.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
